巧解不含参数的极值点偏移问题

姚永亮

（大理州实验中学 云南大理 671000）

不含参数的极值点偏移问题是高考的重点和难点，此类问题在高考中新颖多变，是导数的综合应用问题，其呈现的形式非常简洁，能较好地考查学生的逻辑推理能力，数据处理能力，转化与化归思想，函数与方程思想，数形结合思想等。对于此类问题，学生往往望而生畏，止步不前。

其实，不含参数的极值点偏移问题，往往涉及函数的双零点，是一个多元的数学问题，不管涉及多少变量，途径都是把多元变量转化为一元变量，构造一元函数，分析探究一元函数，此问题将迎刃而解。下面将介绍几种常规策略，希望可以帮助更多的学子迎难而上。

案例：已知函数f(x)=xe-x，且f(x1)=f(x2)，证明：x1+x2＞2

1.1巧构函数

构造函数法是解决极值点偏移问题的常规方法。首先分析f(x1)的单调性与极值点x0，要探究其在极值点x0附近的偏移问题，构造函数F(x)=f(x0+x)-f(x0-x)或G(x)=f(x)-f(2x0-x)x)(x0＞x)，分析F(x)或G(x)，判断出F(x)或G(x)的正负，再结合f(x1)=f(x2)及f(x)的单调性即可解决此问题。

1.1.1构造函数F(x)=f(x0+x)-f(x0-x)(x＞0)

注：通过分析f(x)的极值点x0=1，且f(x)在(-∞，1)上单调递增，在(1，+∞)上单调递减从而知0＜x1＜1＜x2。进而巧构函数F(x)=f(1+x)-f(1-x)（x＞0），分析知F(x)单调递增，故而知f(x1)=f(x2)=f[1+(x2-1)]＞f(2-x2)，此问题即得证。

1.1.2构造函数G(x)=f(x0+x)-f(x0-x)（x＞0）

同上1.1.1知：

∵f(x)=xe-x∴f’(x)=(1-x）e-x∴x∈(-∞，1)时，f(x)＞0；x∈(1，+∞)时，f’(x)＜0

∴f(x)在(-∞，1)上单调递增，在(1，+∞)上单调递减；

f(0)=1，x＞0时，f(x)＞0；又∵x1＜x2且f(x1)=f(x2)；

∴0＜x1＜1＜x2

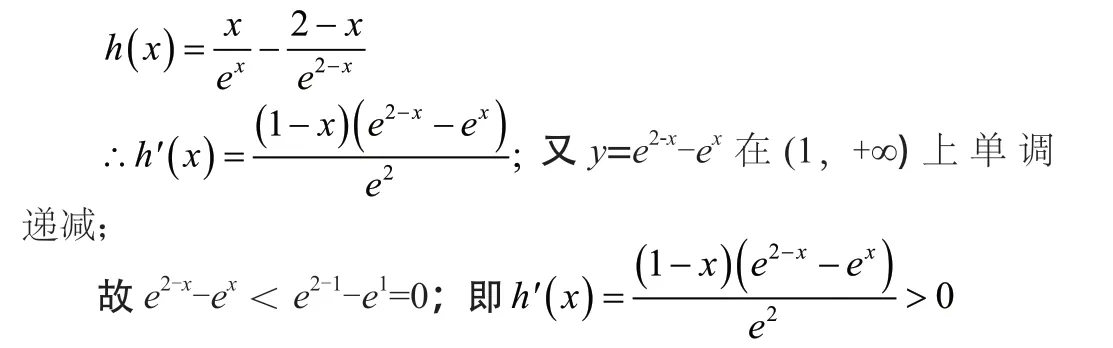
∴h(x)(1，+∞)上单调递增；又h(1)=0；∴f(x)＞f(2-x)；

∴f(x1)=f(x2)＞f(2-x2)；又x1＜1且2-x2＜1

∴x1＞2-x2；即x1+x2.

注：通过分析f(x)的极值点x0=1，且f(x)在(-∞，1)上单调递增，在(1，+∞)上单调递减从而知0＜x1＜1＜x2。进而巧构函数F(x)=f(1+x)-f(1-x)（x＞0），分析知F(x)单调递增，故而知f(x1)=f(x2)=f[1+(x2-1)]＞f(2-x2)，即得证此方法与1.1.1形不同，但本质一样。

1.2巧引变量巧消元

通过对f(x1)=f(x2)分析变换得

1.2.2巧用作差“x2-x1”消元

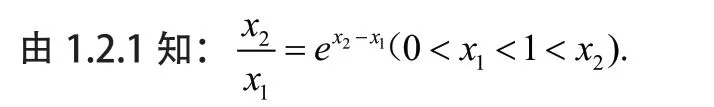
据洛必达法则知：

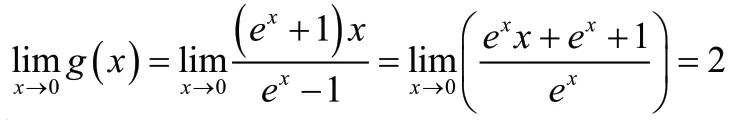
以上几种方法均是为了实现将两个变量转化为单变量的函数或不等式，通过构造一元函数和利用构造新的变元，均达到消元的目的，把问题转化为一元函数，再利用综合法、分析法、洛必达法则等将此问题简单化。几种方法各有优劣，考生若能灵活驾驭这几种方法，便能在导数不含参的极值点偏移问题上发挥自如。

在极值点偏移问题的教学中，常常考查学生的逻辑推理能力，数据处理能力，转化与化归思想，函数与方程思想，数形结合思想等。培养学生的数学核心素养是我们教学的重中之重，我们应从不同角度教会学生发现问题，分析问题，解决问题。但过多过密的刷题，不仅会阻碍学生思维能力的发展，还会使学生疲劳、兴趣降低，窒息学生的思维，只有“闻一知十”解题，才能激发学生浓厚的学习兴趣，促进他们思维的发展。通过本文案例的分析，我们从多个维度教会学生从不同角度解决问题，开拓了学生的思维，真正培养了学生的能力。