双线铁路大直径盾构隧道疏散滑梯可行性研究
2021-10-11刘雨竹王明年郭晓晗胡萧越
刘雨竹,王明年,王 松,郭晓晗,胡萧越,于 丽
(1.西南交通大学土木工程学院,成都 610031;2.交通隧道工程教育部重点实验室(西南交通大学),成都 610031)
引言
截止2020年年底,我国铁路运营总里程已突破至14.6万km,其中,铁路隧道总里程突破1.9万km[1],以台湾海峡隧道为代表的水下铁路隧道工程日益增多[2]。水下铁路隧道中一旦列车着火,将给防灾救援带来很大难度。不同于山岭隧道可设置疏散斜、竖井等方法满足隧道内紧急情况下的人员安全疏散要求,水下铁路隧道由于所处海底,无法设置直通地面的斜、竖井,对于双洞单线铁路隧道,可通过加密横通道的方式互为救援通道,而单洞双线铁路隧道只能通过底部疏散廊道进行竖向疏散。由于早期大断面盾构施工技术还未成熟,断面相对较小,底部没有足够的空间用作竖向疏散空间,因此,采用横通道的横向疏散型式。但随着大断面盾构铁路隧道在水下的应用越来越多,竖向疏散必将成为一种趋势。
目前,底部疏散廊道竖向通道连接可采用封闭楼梯间或滑梯。疏散滑梯常见于公路隧道,铁路隧道通常采用疏散楼梯,如图1、图2所示。国内学者对隧道内及建筑内竖向疏散楼梯、滑梯进行研究,取得了一定的成果。方正[3-4]通过城市水底隧道人员疏散模拟演习,得到在轻松环境下人员没有紧迫感时,武汉长江隧道采用的玻璃钢滑梯人员通行能力为34人/min,建议我国水下隧道采用的竖向疏散滑梯间距宜取60~120 m;曹应龙[5]通过人员竖向疏散试验,得到疏散楼梯的通过能力介于32.7~37.7人/min,平均为36.3人/min,疏散滑梯通过能力介于22~26人/min,平均为24.1人/min,相较于疏散楼梯,疏散滑梯的人员通过能力要弱一些;王梦琪[6]通过研究发现公路隧道盾构段火灾场景下人员采用盾构下部安全通道纵向疏散并增加两条联络横通道能够增加人员疏散效率;邓敏[7]通过Pathfinder对水下单洞双层盾构公路隧道火灾情况下人员通过竖向疏散楼梯疏散的时间进行分析,得到疏散口间距为36 m时,人员可在6 min内疏散完毕;李婷[8]依托武汉两湖隧道,分析影响疏散的疏散楼梯结构参数并进行仿真,通过回归分析确定了纵向疏散楼梯结构参数与疏散时间、人流密度间的函数关系。

图2 公路隧道逃生滑梯
现有学者针对疏散楼梯、滑梯的研究大多基于人员试验来得到其通过能力,或通过仿真模拟给出满足疏散时间要求的疏散口间距。较少从楼梯与滑梯自身设计上给出其最优参数,且研究对象多为公路隧道,较少针对水下铁路隧道进行研究。因此,首先通过数值模拟,明确水下盾构铁路隧道火灾场景下对疏散时间起决定性作用的并不是楼梯(滑梯)通行能力;其次,基于理论公式推导,给出单洞双线铁路隧道采用竖向疏散滑梯时最优滑梯线形,以期为防灾救援设计提供一定参考。
1 工程概况
本次研究依托甬舟铁路金塘海底隧道盾构段。甬舟铁路全长77 km,设计速度250 km/h。金塘海底铁路隧道为长度16.09 km单洞双线隧道,是目前世界上最长的海底高速铁路隧道。该隧道盾构段长11.09 km,外径14.0 m,内径12.8 m,盾构管片厚600 mm,二衬厚300 mm,断面如图3所示。疏散救援设施采用底部疏散廊道,竖向疏散口间距75 m。在铁路隧道运营期间,列车事故多为列车碰撞、列车脱轨,列车碰撞后发生火灾的概率较高,且在碰撞后不能继续行驶,因此,在最不利条件下,出于安全性考虑,对甬舟铁路金塘海底隧道火灾事故列车在隧道内停车人员疏散进行研究。
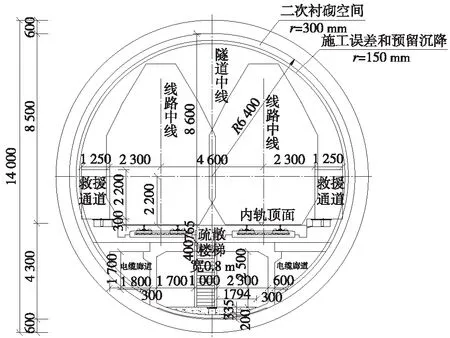
图3 盾构隧道横断面(单位:mm)
2 通过能力影响分析
水下盾构公路隧道火灾场景下疏散时间的影响因素包括人员组成、疏散滑梯的间距、疏散滑梯的通行能力、防护门的宽度等,其中,起决定性作用的是滑梯的通过能力,这与人员疏散路径有关。对于单洞双线铁路隧道,采用底部疏散廊道疏散,TB10020—2017《铁路隧道防灾疏散救援工程设计规范》[9]给出的人员疏散路径为,车上人员→下车至救援通道→沿救援通道绕过事故列车→跨过轨道进入隧道中线→沿竖向通道进入底部疏散廊道,防护门净空尺寸不应小于0.75 m×2.0 m(宽×高)。以车头着火为例,人员疏散示意如图4所示,以此建立模型进行分析。

图4 人员疏散路径
2.1 模型建立
根据TB 10020—2017《铁路隧道防灾疏散救援工程设计规范》规定,动车组采用16辆编组,定员1 229人,考虑超载及乘务人员后为1 495人。人员组成及疏散速度如表1所示。

表1 人员组成及疏散速度
考虑着火车厢的人员在随机停车前已疏散到了相邻车厢内,假设全部人员均匀分布在剩余15节车厢内,则每节车厢约100人。借助人员疏散软件Pathfinder建立疏散模型。每节车厢长25 m,列车总长400 m,两边各留0.5倍车长200 m,模型总长800 m,人员疏散模型如图5所示。

图5 人员疏散模型
原设计中疏散楼梯宽度为80 cm,楼梯宽度直接影响楼梯的通行能力。因此,设定3种工况,对应疏散楼梯通行能力的降低和提高,楼梯宽度60,80,100 cm。其余参数保持不变。
2.2 结果分析
通过计算,得到不同楼梯宽度的疏散时间如表2所示。人员疏散时间随疏散楼梯的宽度增大而减小,但减小幅度很小,因此,对于水下铁路隧道采用疏散廊道纵向疏散,疏散楼梯宽度并不能起决定性作用。
图6给出了典型时刻各工况疏散楼梯口人员聚集情况,可以看出,疏散楼梯宽度的增大有效降低了人员在疏散口聚集,但人员疏散总时间受限于疏散通道上的人员,因此,疏散总时间改变不大,表2数据也反映了这一点。

表2 不同楼梯宽度疏散时间
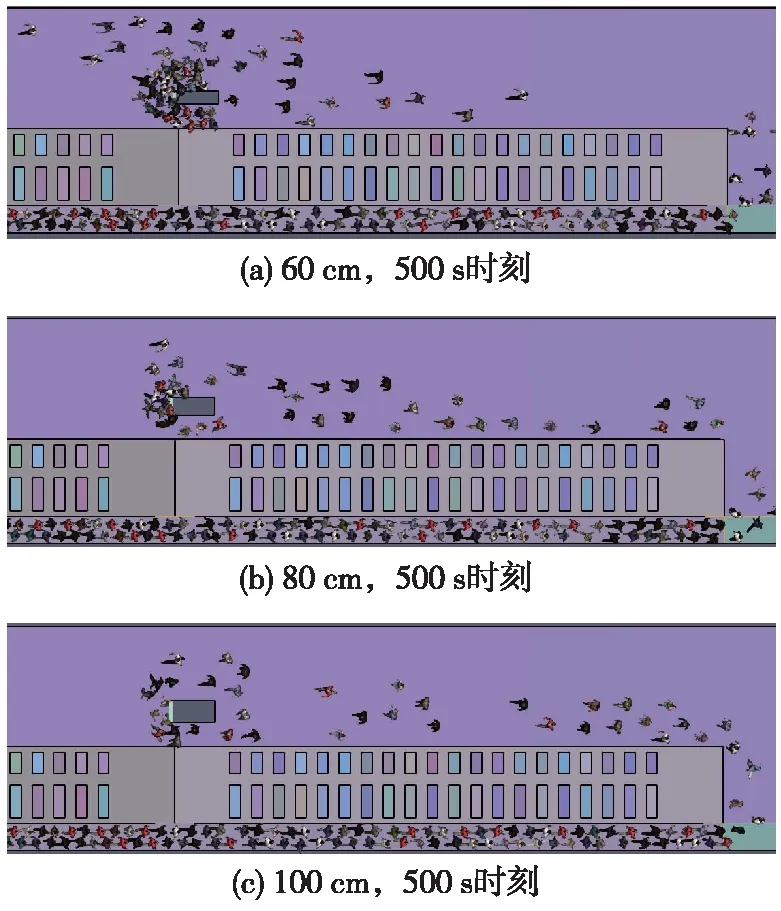
图6 疏散口人员聚集情况
3 纵向疏散楼梯与滑梯对比
相较于水下铁路隧道,竖向疏散在水下公路隧道中已经有了较为广泛的应用,尤其是上海、南京、武汉等地区的城市交通隧道[9-13]。表3列举了部分典型大直径盾构公路隧道所采用的疏散救援设施[14-19]。大致分为3种:横通道、疏散楼梯、疏散滑梯以及相互间组合。

表3 大直径盾构公路隧道疏散救援设施统计
疏散楼梯的通过能力介于30~40人/min,疏散滑梯的通过能力介于20~30人/min。由于滑梯能够同时容纳的人数相对于楼梯要少一些,因此,滑梯平均通过能力要比楼梯低一些。但在紧急疏散情况下,由于人员的恐慌心理,一旦在楼梯疏散过程中出现摔倒、踩踏情况,必将造成严重后果,滑梯则相对安全,且相对于每一个人,个体下滑疏散的时间远小于楼梯,也就更不容易出现恐慌。上文通过数值模拟分析了疏散楼梯宽度并不能起决定性作用。因此,从防止人员恐慌的安全角度可考虑采用类似于公路隧道的疏散滑梯。
4 疏散滑梯参数设计
铁路隧道与公路隧道在竖向疏散通道的位置上存在差异,公路隧道疏散口往往设置在道路两侧[20],铁路隧道则设置在两条线路中间。这样就使得滑梯在空间结构上存在差异:公路隧道逃生滑梯在空间上呈现三维曲面结构,而铁路隧道呈现二维曲面结构,如图7所示。因此,人员在铁路隧道滑梯上的运动相对于公路要简单一些,可简化为二维平面运动模型。
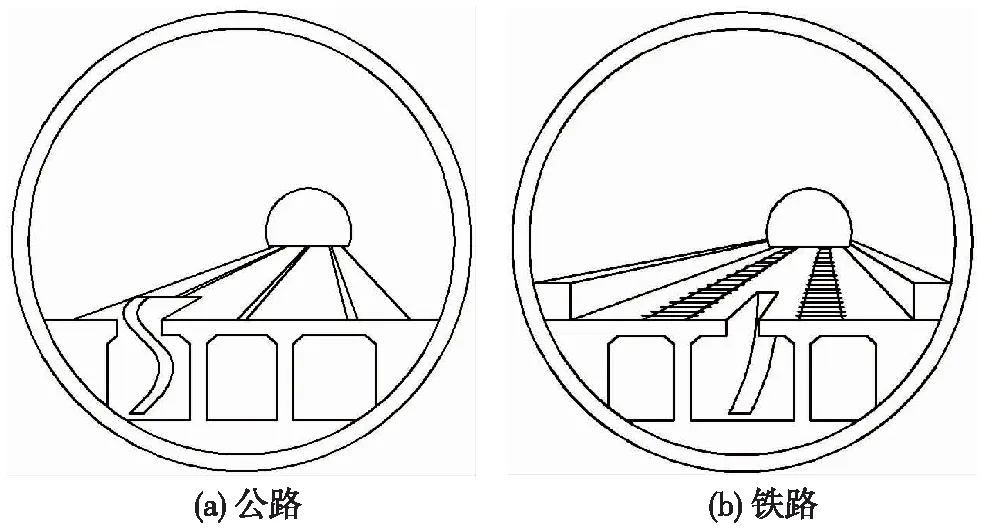
图7 隧道逃生滑梯
4.1 疏散滑梯高度
由图3可以得到,滑梯竖向高度为2.9 m,为方便人员下滑到滑梯底部后能够快速地站起离开滑梯,参考普通座椅的高度,将滑梯底部抬高至离地面40 cm,这样整个滑梯高度为2.5 m。
4.2 疏散滑梯长度
疏散滑梯作为列车上人员在火灾等紧急情况下的逃生疏散通道,需满足人员快速通过并安全到达底部疏散廊道。根据牛顿定律,可以调整滑梯与水平面的夹角,使人员在滑梯上作加速、匀速和减速下滑运动,具体为在刚进滑梯时,AB段做加速下滑运动,接着BC段做匀速运动,最后CD段做减速运动,直至滑到底端时速度为0,从而保证人员的安全快速下滑,如图8所示。
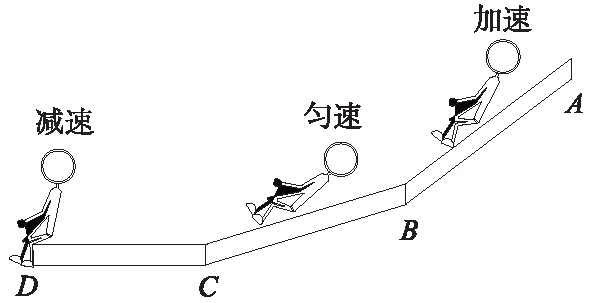
图8 滑梯下滑示意
假设下滑的初速度与到达底端的最终速度都为0,由能量守恒可知,重力势能全部转化为摩擦力做的功,即
GH=Wf
(1)
由牛顿运动定律可知
F=Gsinθ
(2)
N=Gcosθ
(3)
f=μN=μGcosθ
(4)
式中,F为下滑力;G为重力;μ为动摩擦系数;N为正压力;θ为滑梯坡度;H为滑梯竖向高度;Wf为摩擦力做的功。
对于线形为曲线的滑梯,摩擦力做功可采用积分的方法,取滑梯上一段微元,如图9所示。

图9 摩擦力计算示意
摩擦力在每一段微元上做的功为
(5)
积分可得
(6)
解得滑梯的水平长度为
(7)
4.3 疏散滑梯宽度
由于滑梯能够同时容纳的人数相对于楼梯要少一些,因此,滑梯的平均通过能力要比楼梯低。单滑梯宽度约为0.55 m,其横截面呈“U”形;双滑梯宽度约为1.10 m,其横截面呈“W”形。单滑梯和双滑梯的局部形式如图10所示。在满足净空要求的条件下,可增设双滑梯提高其通行能力。
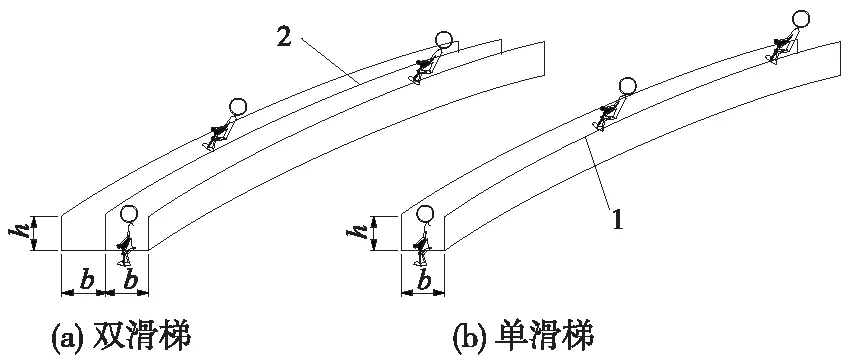
图10 双、单滑梯示意
4.4 疏散滑梯线形研究
滑梯的线形设计应该能使得人员整个下滑的时间最短,因此,简化为如下模型。设O和A是2个不同高度的固定点,两点不在同一铅垂线上,若不考虑摩擦阻力和空气阻力,在重力作用下,粒子M沿着曲线从O点落到A点,曲线存在某一形状时,粒子下落时间最短,如图11所示。
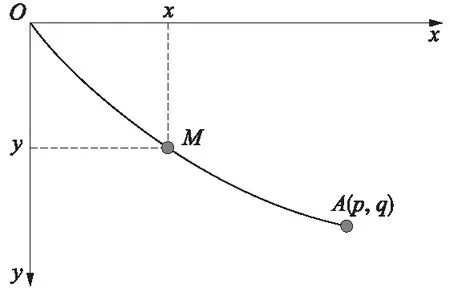
图11 质点M下落示意
设曲线为y=y(x),质点M从O点开始运动后的速度v与其纵坐标有如下关系
(8)
在曲线上质点速度v为
(9)
式中,s为曲线弧长;t为时间。可得
(10)
质点M沿OA段曲线运动所需时间为
(11)
可以看出,质点M沿OA段曲线运动所需时间t是y(x)的函数,而求解最速降线就是在满足边界条件y(0)=0,y(p)=q所有连续函数y(x)中,求出一个函数y使得泛函式取最小值。
推导如下
(12)
且
y(0)=0,y(p)=q
(13)
(14)
其欧拉-拉格朗日方程为
(15)
由于
(16)
故有
(17)
则可得
(18)
上式对θ求导
x=r(θ-sinθ)+x0
(19)
根据曲线过原点(0,0)及(p,q)可求出x0=0及r,所求曲线为
(20)
即为旋轮线,如图12所示。
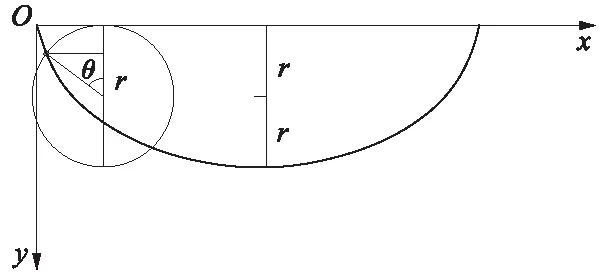
图12 旋轮线示意
曲线是由半径r的圆周上一点在圆沿x轴滚动时产生的。当r从0增大到∞时,摆线的第一拱就扫过整个第一象限,因此,只要选择合适的r,就能使之通过A点。
但实际情况下,人员在下滑中,必定与滑梯壁产生摩擦,由能量守恒可得到
(21)
求得速度为
(22)
质点M沿OA段曲线运动所需时间为
(23)
因此,考虑摩擦的最速降线就是求上式极值曲线。
(24)
通过对几何图形分析,最速降线是与X=μY相切的旋轮线[21]。此时
μ=tan(θB/2)
(25)
θB=2arctanμ
(26)
b=(2μ-2arctanμ)r
(27)
如图13所示,滑梯的线形由3部分组成,竖直段OB、旋轮线段BC、水平段CA。由几何关系可得
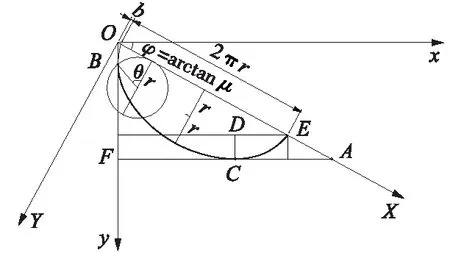
图13 滑梯线形示意
yc=H
(28)
现在问题转化为求yC,设C点在两个坐标系下的坐标分别为(xC,yC),(XC,YC),如图14所示。
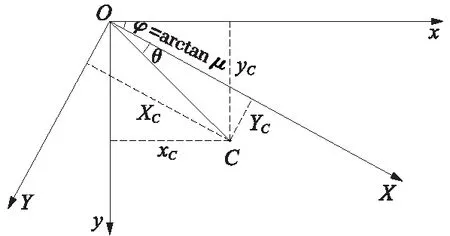
图14 坐标转换示意
(29)
则由式(29)可得
(30)
又因为
(31)
可以求得
(32)
代入式(29)得到
(33)
化简得到
(34)
最终得到
(35)
化简后转化为求f(θ)=1-cosθ+μθ-μsinθ的最大值,得到
f′(θ)=sinθ-μcosθ+μ
(36)
可以求得
(37)
(38)
故滑梯的最速曲线方程为
OB段
x=0
(39)
BC段
(40)
CA段
y=H
(41)
4.5 疏散滑梯材质
通过调研得到,疏散滑梯可采用与游乐设施滑梯同样的材质。采用线型低密度聚乙烯(LLDPE)材料,壁厚5~6 mm,添加抗紫外线稳定剂,防静电,无毒无味,防脱色。具有强度大、表面光滑、色彩鲜艳、安全环保、耐候性好、耐磨、耐晒、耐老化、耐防裂、不易褪色的特点。
5 结论与展望
通过对水下盾构铁路隧道竖向疏散通道选型及设计参数的研究,得到以下结论。
(1)对于特长海底铁路隧道,断面型式为单洞双线时建议采用竖向疏散模式。由于滑梯能够同时容纳的人数相对于楼梯较少,因此,疏散滑梯的平均通行能力低于疏散楼梯。
(2)当水下铁路隧道采用疏散廊道纵向疏散,疏散时间受到人员组成、疏散滑梯间距、疏散滑梯通行能力、防护门宽度等多因素制约,疏散通道宽度不能起到决定性作用。
(3)结合规范及现有工程实例,疏散滑梯具有疏散路径短、个体下滑疏散的时间远小于楼梯、不容易导致人员恐慌等优点,因此,大直径水下盾构铁路隧道竖向通道可采用滑梯型式。建议滑梯高度取2.5 m,宽度采用双滑梯形式,使用线型低密度聚乙烯(LLDPE)材料,线形满足最速曲线方程。
目前,在大直径盾构铁路隧道中疏散滑梯还未得到大面积推广应用。而本次研究提出大直径盾构隧道纵向疏散滑梯的基本设计参数,证明了疏散滑梯具有一定可行性,为大直径盾构铁路隧道疏散滑梯的设计及选型提供参考。但疏散滑梯不能使得人员疏散到安全距离之外,还需通过疏散通道上到行车层等待后续的救援列车救援,具有一定局限性。鉴于水下铁路隧道人员疏散的复杂性,在未来具体工程疏散形式比选中须考虑隧道整体抗灾能力及外界综合救灾能力,必要时可结合全尺寸疏散试验加以验证,从而最大限度地保证人员的生命财产安全。
