结构光3D点云的PIN针针尖提取

杜钦生， 李丹丹,， 陈 浩， 李雄飞

(1. 长春大学 计算机科学技术学院， 吉林 长春 130022；2. 苏州深浅优视智能科技有限公司， 江苏 苏州 215000；3. 吉林大学 计算机科学与技术学院， 吉林 长春 130012；4. 长春大学 旅游学院 工学院， 吉林 长春 130122)

1 引 言

电子连接器引脚是工业接插件的关键部位，在生产过程中会存在翘脚、歪脚、缺脚和断脚等问题。引脚会直接决定产品的质量，因此对其位置的检测要求也非常严格。一方面，人工检测速度慢，误检率高，劳动力大[1]；另一方面，运用机器视觉进行质量检测，PIN针检测均是基于硬件为2D相机、镜头加上光源在一定的工作距离对工件进行拍摄[2-4]，得到的图像为单通道灰度图或三通道彩色图，但像素值均是灰度值的2D平面图，这种方法对硬件的选型及摆放需要精准设置，且光照等外部因素会影响图片质量，最重要的是相机拍摄的空间物体投影到平面上会丢失很多关键信息，导致结果误差较大。相比之下，三维点云数据增加了深度信息，具有非常灵活、强大的表示能力，因此在机器视觉领域的应用越来越广泛，成为近几年来的研究热点[5-6]。但由于相机拍摄角度、人为因素、物体表面自身遮挡等问题，在无序点云中存在大量噪点，包括体外飞点、离群成簇噪点、混杂的毛刺噪点等。目前国内外学者提出了一些点云去噪和分割的方法[7]。袁华等通过将噪声进行分类，采用不同滤波算法对噪声去除的方法，提高了计算效率且避免了细节失真[8]。王晓辉等通过直接计算曲率及法向距离将点云数据分成平滑区域和尖锐区域进行去噪，可以说是按照点云的特征进行分类去噪，但是点云数据越多其法向量计算时间越长[9]。同样，吴禄慎等通过对点云曲率的计算将点云分成不同区域，然后采用平均滤波和自适应双边滤波算法去噪，但是在计算微分几何信息时耗时长，并且如果离群点很多时很难进行分类，则会出现较大误差[10]。

本文提出一种基于结构光3D点云的PIN针针尖平面提取方式。通过结构光及工业相机采集点云信息。由于在工业中采集的点云数据量非常多，但又只对工件的某一部分进行提取处理，所以采用点云的特征进行分类去噪并提取[11]。首先使用直通滤波去除大量非目标点云。对目标点云进行粗提取，采用欧氏聚类分割算法，满足工业上对速度性和准确性的要求。对于电子连接器引脚在工业中的高精度需求，对分割后的点云进行法矢量估算，并与基准平面的法向量进行对比，从而提高引脚重心的计算精度。该方法吸取了前人算法的优点，且对无序点云和网格化后的点云均适用，既能测量PIN针针尖高度，又能通过该方法在保留PIN针针尖细节的同时去除了干扰的点云数据，满足了在实际工业上电子连接器引脚检测的准确性、速度性、高精度的要求。

2 面结构光技术

三维测量技术中主动式三维测量采用结构照明方式，能快速、高精度地获得物体表面三维信息，具有精度高、测量速度快、成本低等优点，非常适合在光照不足、缺乏纹理的场景下使用。因此，本文采用结构光技术获取工件点云数据信息[12]。如图1所示，结构光由投影仪和相机两部分组成。通过投影仪投射特定的光信号覆盖到物体，然后利用相机收集物体信息[13]。面结构光三维测量方法的基本原理是将计算机生成的已知相位的光栅条纹图像投影到被测物体轮廓，从与投影方向成一定角度的方向观测，因为物体位置及外面深度差别，光栅条纹的相位发生变化。变形的光栅携带了物体的三维信息，通过解相和相位展开等技术，可得出相位信息，进而利用三角法根据相位与物体空间坐标的转化关系求出物体的三维坐标[14]。

图1 结构光三维测量原理Fig.1 Three dimensional measurement principle of structured light

3 PIN针针尖提取

3.1 PIN针针尖提取

3.1.1 直通滤波

点云中滤波方法有很多。实际应用中电子连接器引脚在实际传送带进行检测时，放置的位置均是在同一平面(高度)下，因此引脚的针尖高低差距不大。基于这一特点，直通滤波可以很好地将坐标系某一轴的大面积离群点去除，适合用于偏离主体点云比较远的离群点和非目标点，达到粗处理的目的，非常简单实用[15]。其基本原理是对点云模型周围的某点到三维扫描仪的距离与给定的阈值进行比较，剔除不在给定阈值之内的噪声点云，保留在阈值之内的模型点云。

给定散乱点云数据P={p1,p2,p3,…,pn}(共n个点)，直接根据工件拍到的点云图像信息确定在某一方向轴上进行阈值选择进行阈值分割，设置保留的点云数据中点的坐标在某方向轴的最小值dmin和最大值dmax。去除阈值范围以外的冗余点，将目标点云分割出来，从而去除背景点云。图2为原始拍摄的电子连接器点云图，图中的颜色是按照总体点云数据的高度进行渲染，从低到高依次为赤、橙、黄、绿、青、蓝、紫，其中由蓝至紫为PIN针的针尖部分。从图中可以看出，PIN针针尖的点云在所有点云中面积较小，因此存在大量不同方向、不同位置的无价值点云及离群点云，且离群点云大小也不尽相同。图3所示为阈值分割与直通滤波之后的点云图，从图中可以看出该滤波方法有效去除了电子连接器的底面点云，将PIN针的针尖点云提取出来。

图2 电子连接器原始点云图Fig.2 Points cloud chart of electronic connector

图3 直通滤波后点云图Fig.3 Points cloud chart after straight through filtering

3.1.2 欧氏距离聚类分割

从图3的点云图可以看出，阈值分割与直通滤波可以高效地过滤掉阈值之外的非目标点云，但无法滤除在阈值之内的散乱噪点。图4为图3旋转放大后某一区域内的点云图，可以看出针尖上存在大量噪点，且阈值分割无法精准得到PIN针的针尖点云。点云分割可以划分出多个点云子集，保证每块点云子集的属性相同或者相近[16]。基于欧式距离的聚类分割是利用量化的方式来定义每个样本的相似程度[17-18]，从而去掉散乱点云噪点。在实际工业中，3D相机拍摄在同一位置下同一个物体且物体不发生形变条件下，点云图片也会发生细微差异，点云数据中的噪点也会时有时无或发生位置的改变，且引脚针尖的点云数据与噪点相比，距离是有效的差异因素，因此采用欧式距离聚类分割算法去除噪点。

图4 直通滤波后点云存在的噪点Fig.4 Noise points existing in the point cloud after through filtering

在欧式距离聚类分割中，对于散乱点云的按序查找，本文选择采用 KD-tree法。KD树是基于二叉树可以实现多维数据的组织和储存的一种结构形式。KD树每一个节点都可以划分为两个空间，直至节点中包含的数据少于设定值[19]。

本文中的欧氏距离聚类分割可以同时去除目标点云附近的背景点云及目标点云周围的散乱噪点，从而准确地找到针尖点云。按照点与点之间的间隔作为判断是否为同一类点云的指标。针对点云数据剩下的Q个点，需要定义距离阈值t，小于阈值的点放在同一簇中，大于阈值的点则不放进该簇中[20]。则每两个点之间的间隔d的计算公式为：

(1)

其中(xi,yi,zi)、(xj,yj,zj)的i,j∈n，是任意两点在该工件坐标系的下标。

除此之外，在欧氏聚类分割中，增加一个判断是否属于同一局内点的指标，即簇内点的数量。电子连接器每个引脚的针尖外观、面积都接近一致大小，因此每一簇内的点云数量都在某一数值上下范围跳动，因此根据该指标可以判断该类点云是否为针尖点云。根据面积可以设定针尖点数量的阈值范围，即最小值nmin与最大值nmax。在这个阈值范围内则保留该类点云，否则，过滤掉该类点云。欧式距离聚类分割的详细算法流程：

(1)输入点云数据P，创建一个KD-tree数据结构。

(2)随机选取P中一个点pi进行近邻搜索，计算pi与搜索到的每一个点的距离，将小于距离阈值点保留在类N中。

(3)对N中的每一个点Ni进行近邻搜索，同样判断搜索到的每个点到Ni的距离，如果符合要求则放入N中。直到N没有新的点加入为止，完成搜索进程。将N中一簇聚类加入点云索引T中，重置N。

(4)遍历P中所有点，重复(2)、(3)操作。

(5)设置一个聚类需要的最小点数目m1和最大点数目m2。

(6)迭代访问点云索引T，保留点数在m1与m2之前的点云子集，完成聚类分割。

欧氏距离聚类分割后的点云图如图5所示，从图中可以看出该算法过滤掉了图3中存在的离群点及引脚中小的稀疏噪点，有效地去除了非目标点云并准确提取了PIN针的针尖。图6为图5旋转放大后某一区域内的点云图。从图6可以看出，分割后的目标点云虽被准确地提取出来，但在针尖上存在少量上下浮动的噪点，且实物中该PIN针的针尖为平面，上下浮动的噪点对针尖测量的精确性存在一定程度的影响。

图5 欧氏聚类分割后点云图Fig .5 Points cloud chart after Euclidean distance clustering segmentation

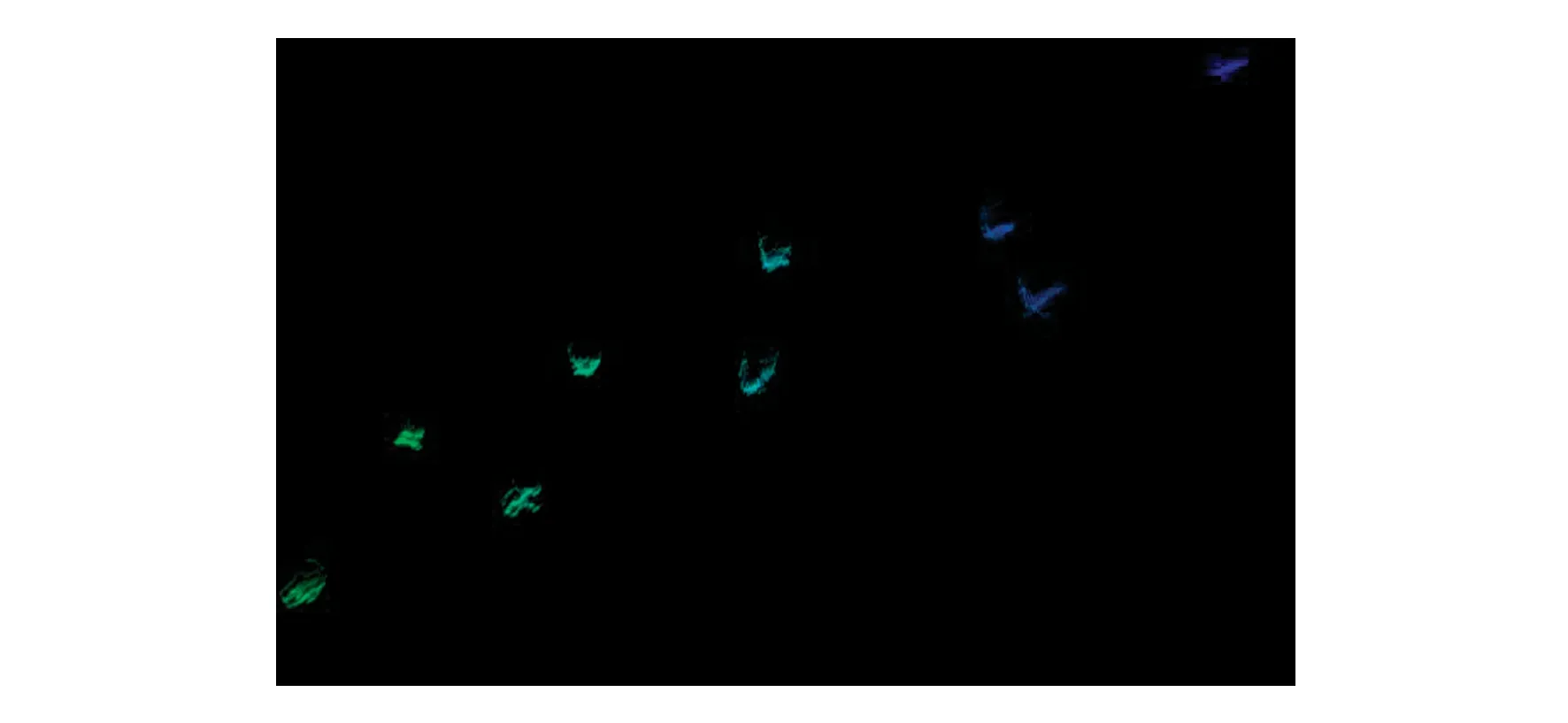
图6 欧氏聚类分割后点云侧视图Fig.6 Points cloud side view after Euclidean distance clustering segmentation

3.2 针尖平面滤波

法向量估计是点云处理的重要属性之一。点云中每一点的法向量夹角及曲率值均不随物体的运动而改变，具有刚体运动不变性。且法向量计算可以使点云既保持特征又能平滑区域。由于引脚中心提取的准确性非常高，否则就会对精度造成损失，又因为聚类分割后的点云数量并不是十分庞大，所以采用法向量估计对分割后仍然具有上下浮动噪点的针尖点云(图6)进行细化处理。

目前已有的点云法向量估计方法可以分为3种类型：基于局部表面拟合的方法[21]、基于Delaunay/Voronoi的方法和基于鲁棒统计的方法[22-23]，根据实验结果及电子连接器引脚的特点，本文采用文献[24]提供的方法结合实际情况计算引脚点云的法向量。

本文方法中，分割后的点云数据P={p1,p2,p3,…,ps}(共s个点)，点集中任意点pi的最近k邻域可表示为N(pi)。通过在pi及其k邻域上采用加权最小二乘拟合来定义一个平面P，该平面近似为局部切平面。对每个点的所有相邻点添加高斯(Gaussian)权重函数，即式(2)中的θ(·)。这意味着距离点对法向量估计结果会产生不同的影响，从而可以得到较好的结果：

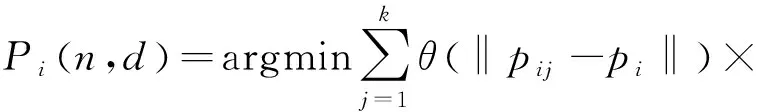
(2)

其中n为平面P的法向量，d为P到坐标原点的距离。同时法向量n需要满足‖n‖2=1，θ(·)为高斯权函数，此处的加权函数以p中当前点与其k邻域上的点的距离作为参考，其中pii为pi的k邻域上任一点(j∈N(pi))，pi为点云数据p中任一点(i∈s)。

电子连接器引脚的底座作为检测时的基准，通过在基准底座上拟合一个平面P2来去除引脚点云的噪点。基准平面的拟合采取稳定性高、速度快的最小二乘法。

拟合平面P2表示为：

(3)

其中n2为平面P2的法向量，d2为P2到坐标原点的距离。

法向量滤波的最后一步是测量P2的法向量与P的法向量的夹角α。对夹角设置阈值，在阈值内的点则保留，阈值之外的点则判定为噪点，进行剔除。图7为法向量滤波后的点云图，从图中可以看出法向量滤波并没有改变针尖形体特征，也没有将目标点过多的滤除造成失真的情况。图8是图7经过放大旋转后其中一个引脚针尖的点云图。从图中可以看出，该算法将针尖平面紧密相连的上下范围跳动的点也可以很好地去除，从而得到近似在同一平面的点云数据，避免噪点数据的干扰，对下一步针尖中心点的提取更加准确稳定。

图7 法向量滤波后的点云图Fig.7 Points cloud chart after normal vector filtering

图8 单个引脚针尖平面点云Fig.8 Single pin tip plane point cloud

4 实验结果与分析

4.1 不同工件去噪参数设置及结果分析

为了验证本文算法的准确性，实验采用工业上常用的电子连接器引脚进行中心点提取，通过dpt 3D相机进行拍摄，操作是在主频2.90 GHz，8 GB内存，Window10操作系统环境下，利用VS2017实现。表1为4种工件进行引脚针尖提取的最优参数设置。

表1 多个工件引脚针尖提取的最优参数设置Tab.1 Optimal parameter setting for multiple workpiece pin tip extraction

其中直通滤波的参数：d为方向轴的选择，dmin为坐标范围最小值，dmax为坐标范围最大值；欧氏聚类分割的参数：t为点距离阈值，nmax为针尖最大点数目，nmin为针尖最小点数目;法向量滤波的参数：α为法向量余弦角。

图2与图7为工件1原始点云图及提取的针尖平面点云图，图9～图14为另外3种工件的点云图。其中图9、图11、图13为3种工件原始点云图，图10、图12、图14是采用本文算法根据表1的参数提取的对应的针尖平面点云图。工件1～4形状不同，引脚位置不同、列数不同、大小不同、个数不同，但均能准确提取引脚针尖平面的点云，滤除背景点云，剔除引脚针尖周围的细小噪点及针尖上的小范围的干扰点，从而对引脚的高度测量提供了准确的前提条件，说明本文算法具有普适性。

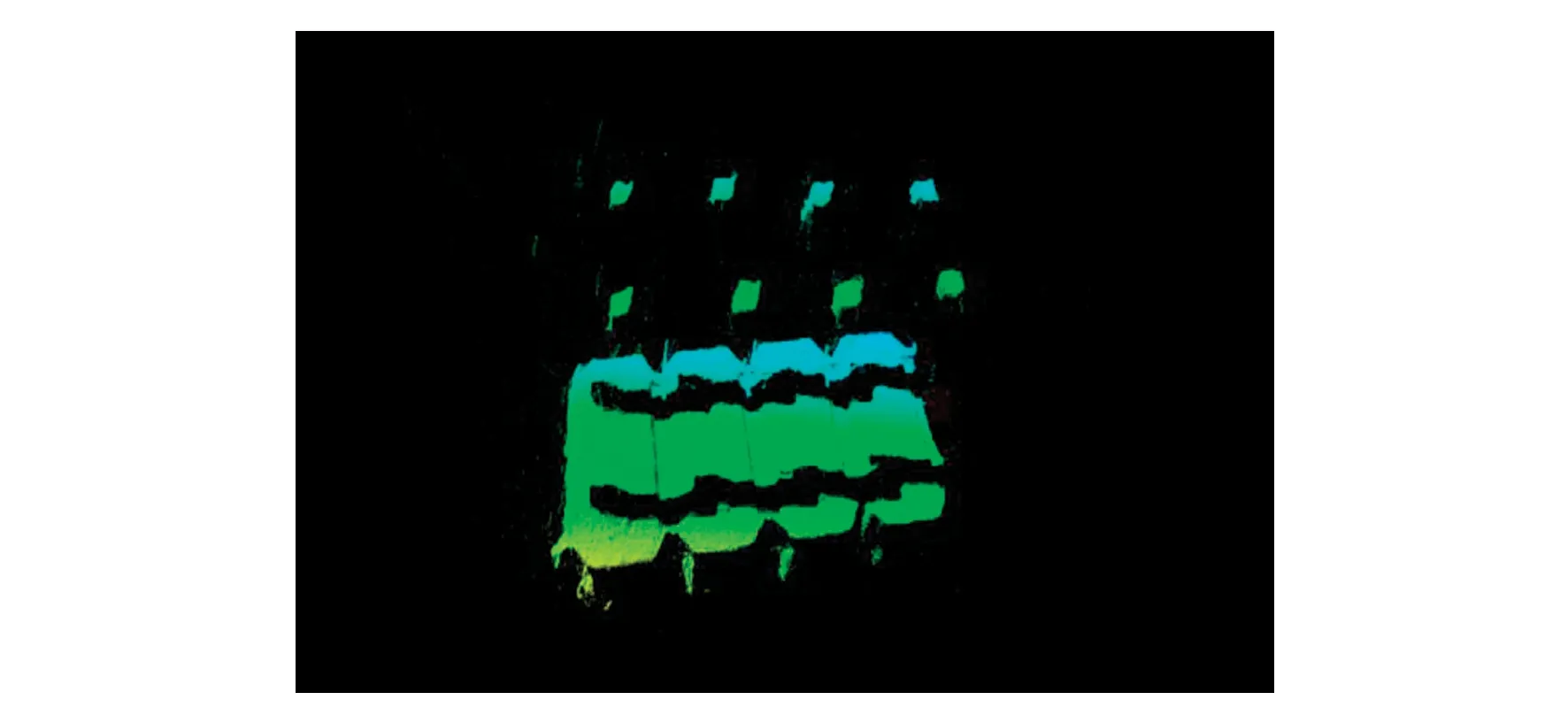
图9 工件2原始点图Fig.9 Original point cloud of Workpiece 2

图10 工件2针尖平面图Fig.10 Pinpoint plane of Workpiece 2

图11 工件3原始点云图Fig.11 Original point cloud map of Workpiece 3

图12 工件3针尖平面图Fig.12 Pinpoint plane of Workpiece 3

图13 工件4原始点云图Fig.13 Original point cloud of Workpiece 4

图14 工件4针尖平面图Fig.14 Pinpoint plane of Workpiece 4

4.2 平面度检测

分别计算每个工件的每个引脚针尖平面的平面度。计算得到的引脚针尖平面的所有点数据与基准面的距离，将最大值与最小值做减法即为一张图所有引脚针尖的平面度。与原始图像每个引脚针尖平面的平面度进行对比，原始图像计算平面度步骤如下：经过直通滤波与聚类分割后，计算引脚针尖平面所有点到基准面的距离，将得到的最大值与最小值做减法，得到原始图像针尖平面度。对比结果如表2所示。

表2 本文算法计算的针尖平面度与原始图像的针尖平面度对比

根据表中数据得出，本文算法平面度约是原始图像计算的针尖平面度的0.5倍，相较于原始图像，本文算法得到的针尖平面点云数据更平整，无效噪点更少，体现了法向量滤波在引脚针尖检测的重要性，因此本文算法在提取引脚针尖平面上的点云数据具有很好的准确性。

4.3 高度测量

对工件1进行PIN针的高度测量。由于通过3D测量可直接得到PIN针的三维坐标点，因此工件1采用本文算法提取的针尖点云计算每根针尖的中心点坐标c(x,y,z)，计算公式为式(4)，再根据式(5)计算中心点到基准面的距离即为PIN针的高度H。

(4)

(5)

其中(xi,yi,zi)为工件1提取到的k个针尖点坐标(i∈k)。a、b、c、d为通过公式(3)得到的基准平面的系数。

重复实验10次，图15为工件1中引脚高度测量的10次统计结果。工件的标准值为2.5(±0.05) mm，从图15可以看出，所有针尖高度均在真值以内，表3为图15中19根引脚测量10次得到的每根引脚的最大值、最小值、差值、标准差。从表中得知，引脚的最大值与最小值之间的差值在0.003 mm以内，说明本文算法可实现的精度在±0.005 mm以内，准确性较强；同时标准差在0.001以内，说明本文算法的稳定性强。因此，本文算法对PIN针针尖提取结果准确有效且鲁棒性强。

图15 工件1中19根引脚高度测量10次统计图Fig.15 Statistical diagram of 19 pin height measurements for 10 times in workpiece 1

表3 工件1中19根引脚测量10次统计表

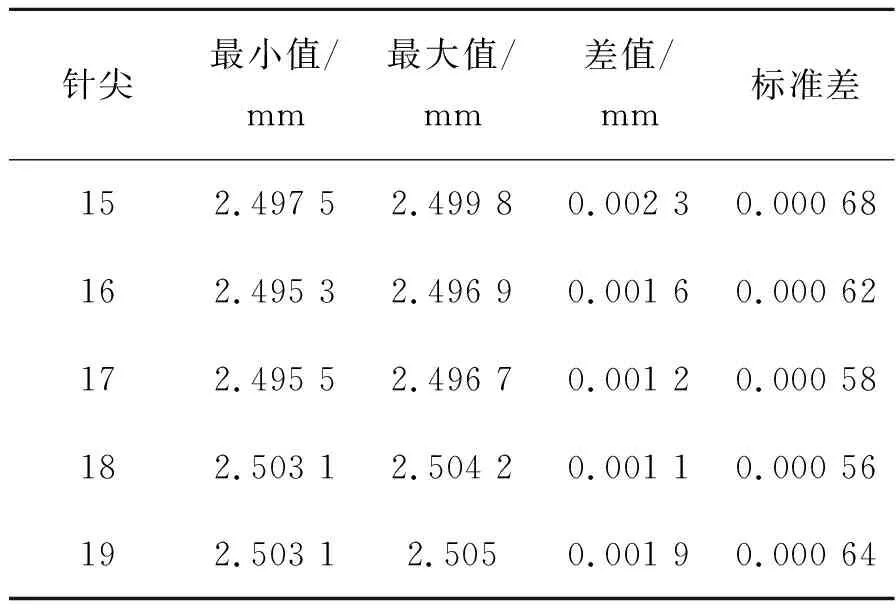
续 表

4.4 与现有方案对比

采用500万像素2D相机，25 mm景深的镜头，光源为平行背光，曝光时间为1 000 ms对工件3进行采图(图16)，并根据近几年研究的基于机器视觉技术的文献[4]计算PIN针的高度。首先使用3×3的中值滤波对图像进行去噪处理，梯度锐化法清晰2D图像轮廓，Qtsu算法进行阈值分割，然后使用Canny算子进行边缘检测，Harris算子进行角点检测及最小二乘法进行直线拟合，从而通过简单的数学运算公式对2D图像进行引脚高度的测量。

图16 工件3侧面灰度图Fig.16 Gray-scale images of workpiece 3 sides

表4为根据现有2D相机拍摄方案与本文方案测得的针尖高度进行数据统计，图17为表3、4数据折线图。通过精度为1 μm的螺旋测微器检测针尖距离基准面的标准高度为(6.000±0.005)mm，通过表3和图17可知，本文算法更接近真值，更准确，且在范围内高度值跳动小，鲁棒性较好。表5为本文算法与现有算法的运行时间测试，由在相同电脑上(未使用GPU)的测试结果可知，本文算法效率更高，时间更快。

表4 工件3的PIN针高度测量结果Tab.4 Height measurements of ten pins in different directions (mm)

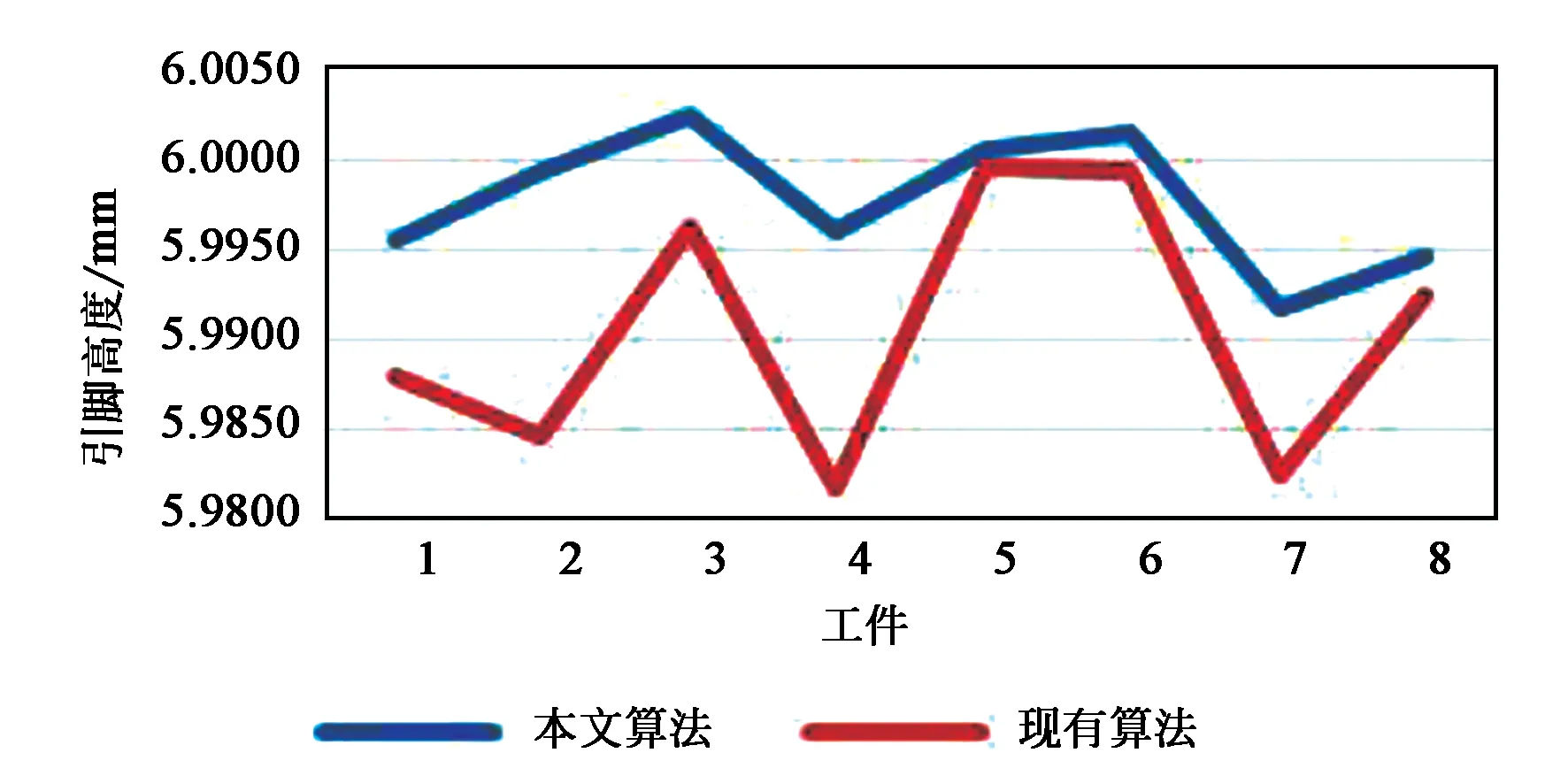
图17 不同方法计算针尖高度统计图Fig.17 Statistic chart of tip height was calculated by different methods

表5 PIN针检测运行时间Tab.5 Run time of pins (ms)

5 结 论

在工业生产中对PIN针的检测精度要求越来越高，本文采用结构光技术对PIN针的针尖平面在三维空间中进行提取。根据点云数据存在毛刺现象、孔洞、离群点及大量不同类型的噪点等问题，首先利用几何特性和直通滤波进行点云粗提取，快速准确地行定位目标点云并去除大量非目标点云及离群点。然后使用欧氏距离聚类分割算法，采用对点云数量进行范围限制及欧式距离阈值设置的方式对目标点云进行分割，稳定有效地去除目标点云附近的小范围噪点，更精细化地提取PIN针针尖。最后通过对目标点云法向量与基准面法向量夹角的判断方法筛选符合阈值夹角的针尖点云，有效且精确地去除目标点云内不平整的噪点，对针尖点云数据的提取更加准确。实验结果表明，本文算法的标准差在0.001以内，比现有方案精度高，鲁棒性好，用时提高了122.6 ms。