构建“将军饮马模型”巧求最小值——一道课本例题的拓展探究

黄旭华

（浙江省杭州采荷中学教育集团 浙江·杭州 310000）

线段和最小值、三角形周长最小值、四边形周长最小值问题是中考中经常出现的一类探究性问题，综合性强、思维含量高、应用性广等特点，能有效的考查学生的核心素养。这类问题通常以角、三角形、四边形、圆等几何图形或直角坐标系、函数为背景，考查学生综合运用所学知识分析问题和解决问题的能力。此类题型对学生具有较强的挑战性，在评价上有很好的区分度，常常借助“将军饮马模型”，根据“两点之间线段最短”这一基本原理解决最小值问题。笔者以典型常见的问题为例进行研究，以期抛砖引玉。

1 构建“将军饮马模型”，形成解题方法

课本原题：浙教版八上数学教科书第50页例2：

如图，直线l表示草原上的一条河流。一骑马少年从A地出发，去河边让马饮水，然后返回位于B地的家中。他沿怎样的路线行走，能使路程最短？作出这条最短路线。

【分析】此题有两定点A,B和一条定直线l，通过一个定点轴对称，将两条线段之和转化为一条线段之长，根据两点之间线段最短，就能确定最近点。如图，设点P是直线上任意一点，连结AP，BP。以直线l为对称轴，作与线段AP成轴对称的线段A＇P，则AP+BP=A＇P+BP。显然，当点A＇，P，B三点同在一直线上时，A＇P+BP最短，即路程最短。

【解】如图，作点A关于直线l的对称点A＇，连结A＇B，交直线l于点C，连结AC。骑马少年沿折线A-C-B的路线行走时路程最短。

下面给出证明：

设点P是直线l上任意一点，连结AP，AP＇。

由作图知，直线l垂直平分AA＇，

则AC=AC＇，AP=A＇P（线段垂直平分线上的点到线段两端点的距离相等）

∴AP+BP=A＇P+BP≥A＇B，

A＇B=A＇C+BC=AC+BC，

即AP+BP≥AC+BC，

所以沿折线A-C-B的路线行走时路程最短。

“将军饮马”问题是中考的热点问题之一，生活中如水泵、公交站、网络基站、送牛奶点的位置设置等问题，都是对“两点之间线段最短”这一原理的应用。在几何问题中求线段和的最小值，求三角形或四边形周长的最小值时，都要构造“将军饮马模型”来解决。解决这类问题的关键是将定点进行轴对称，然后通过连线，进而转化为两点之间线段最短来解决问题。这类问题通常会演变出三种模型：（1）两定点和一定直线；（2）一定点和两定直线；（3）两定点和两定直线。

2 运用“将军饮马模型”，注重知识迁移

2.1 角中最小值

【例1】尺规作图：如图1-1，点P是∠MON内的一点，分别在角的边OM、ON上作点A、点B，使△ABP的周长最小。

【分析】本题主要考查学生的动手实践能力，由题意可判断属于一定点和两定直线模型。通过画图，运用轴对称性质可得出：PA=P1A，PB=P2B，C△ABP=PA+PB+AB=P1A+P2B+AB=P1P2，因为两点之间线段最短，所以此时△ABP的周长最小。

【作法】如图1-2。

（1）过点P作关于直线OM的对称点P1；

（2）过点P作关于直线ON的对称点P2；

（3）连接 P1、P2，分别交 OM、ON 于点 A、点 B。

点A点B即为所求作的点。

【变式训练1】如图1-3，点P、Q为∠MON内的两点，分别在OM，ON上作点A、B，使四边形PAQB的周长最小。

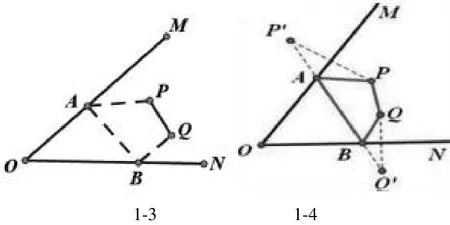
【提示】本题属于两定点和两定直线模型。如图1-4，分别作点P、Q关于直线OM、直线ON的对称点P＇、Q＇，连接P＇Q＇交∠MON的两边OM、ON于点A、B，使四边形PAQB的周长最小。

2.2 三角形中的最小值

【例2】如图2-1，在△ABC中，AB=6，AC=8，BC=10，EF是BC的垂直平分线，P是EF直线上的一动点，求PA+PB的最小值。

【分析】如图2-2，根据题意，设EF与AC的交点为点P，连接BP，由垂直平分线的性质，则BP=CP，得到PA+PB=PA+PC=AC，即可得到PA+PB的最小值。本题考查了垂直平分线的性质，三角形两边之和大于第三边，两点之间线段最短等知识。解题的关键是应用“将军饮马模型”正确找出点P的位置。

【解】如图2-2，根据题意，设EF与AC的交点为点P，连接BP。

∵EF是BC的垂直平分线，

∴BP=CP，

∴PA+PB=PA+PC=AC=8，

∴PA+PB的最小值为8。

【变式训练2】如图2-3，已知等边△ABC的边长为6，点D为AC的中点，点E为BC的中点，点P为BD上一点，求PE+PC的最小值。

【提示】如图2-4，由题意可知点A、点C关于BD对称，连接AE交BD于点P，由轴对称的性质可得，PA=PC，故PE+PC=AE，由两点之间线段最短可知，最小值为PE+PC=PE+PA=AE.由于点D为AC的中点，点E为BC的中点，借助等腰三角形三线合一的性质，勾股定理，易求得即PE+PC的最小值是

2.3 四边形中的最小值

【例3】如图3-1，在矩形ABCD中，AB＝5，AD＝3。动点P满足S△PAB＝ S矩形ABCD。则点P到A，B两点距离之和PA＋PB的最小值为（ ）

【分析】本题属于两定点和一定直线问题，但定直线未知，所以要先确定这条直线。解决的要点是先根据矩形面积不变，判断三角形面积不变，知道三角形AB边上的高不变，可确定点P在定直线EF上运动，然后根据“将军饮马模型”找出点P所在的位置；最后根据勾股定理即可求出最小值。

【解】如图3-2所示，设△PAB底边AB上的高为h。

在AD上截取AE＝2，作EF∥AB，交CD于F，故P点在直线EF上，

作点A关于直线EF的对称点A′，连接A′B，交直线EF于点 P，此时 PA＋ PB最小，且 PA＋ PB＝ A′B＝

【变式训练3】如图3-3，在矩形ABCD中，AB＝3，BC＝4，E为边BC的中点。若F为边AB上的一个动点，求△DEF周长的最小值。

【提示】如图3-4，本题中点D、E两点是固定点，点F是在定直线AB上的动点，求△DEF周长的最小值，只要根据“将军饮马模型”找出点F点所在的位置，然后运用勾股定理即可求出最小值为

2.4 圆中的最小值问题

【例4】如图5，AB、CD是半径为5的⊙O的两条弦，AB＝8，CD＝6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA＋PC的最小值为_______。

【分析】本题属于两定点和一定直线模型，点A、B两点关于MN对称，因而PA＋PC＝PB＋PC，即当B、C、P在一条直线上时，PA＋PC的最小，即BC的值就是PA＋PC的最小值。本题考查了轴对称确定最短路线问题，熟练运用垂径定理，根据轴对称性找出对称点，通过连线找到最近点P的位置，是解决最小值的关键。

【解】如图4-2，连接OA，OB，OC，作CH垂直于AB于点H。

根据垂径定理，得到

【变式训练4】如图4-3，在⊙O中，AB是⊙O的直径，AB是AB上一动点，则CM＋DM的最小值是_______cm。

【提示】如图4-4，作点C关于AB的对称点C'，连结C'D与AB相交于点M，根据轴对称确定最短路线问题，点M为CM＋DM的最小值时的位置，根据垂径定理可得然后根据弧的度数判断C'D为直径，从而解得CM＋DM的最小值是8cm。

2.5 直角坐标系中的最小值

【例 5】如图 5-1，在直角坐标系中，已知 A(0，2)、B(6，4)，点P在x轴上，当三角形ABP的周长最小时，求点P的坐标。

【分析】本题符合“将军饮马模型”，属于两定点和一定直线模型。根据轴对称性在x轴上先找出点P所在的位置，然后求直线A＇B的关系式，就能求出P点的坐标。找到问题本质，突出数学模型思想的重要性。

【解】如图5-2，过点A作关于x轴的对称点A＇，连接BA＇交x轴于点P。

因为A(0，2)关于x轴的对称点A＇，所以A＇(0，-2)，

设直线A＇B的关系式为y＝kx＋b，把A＇、B两点代入得：

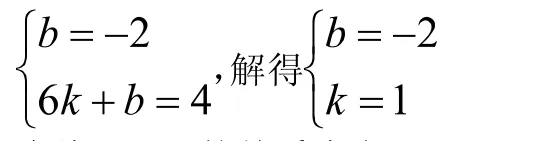
直线A＇B的关系式为y=x2

当 y=0时，x=2，

所以P点的坐标为（2，0）.

【变式训练5】如图5-3，已知抛物线y＝ax2＋bx＋c经过 A(－ 1，0)、B(3，0)、C(0，3)三点，直线 l是抛物线的对称轴。设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；

【提示】如图5-4，本题以抛物线为背景，研究三角形周长的最小值，看似三条线段和最小，实质仍是两条线段和最小问题，即PA+PC的最小值，符合“将军饮马模型”，运用三角形相似或一次函数关系易求得点P的坐标是（1，2）。

3 两点思考

3.1 在运用“将军饮马模型”解决同类型问题的步骤如下

（1）分析题目的背景，确定模型；（2）根据题意找出定点；（3）根据动点在哪条直线上运动，即可确定该直线为对称轴；（4）作定点关于对称轴的对称点；（5）将定点与对称点连成线段或两个对称点连成线段，即可得到最近点。

3.2 教学时回归教材，体会数学模型的力量

数学建模是通过建立模型的方法求得问题，探究数学活动过程，几何模型在整个学习过程中发挥着重要作用。学生要通过观察、分析、选择、判断等数学活动，完成模型构建，经历“问题情境—建立模型—探究结果”，从而形成数学方法，渗透建模思想。