基于倍压单元耦合电感高增益DC/DC 变换器
2021-10-10荣德生袁亚松孙瑄瑨刘飞扬
荣德生,袁亚松,孙瑄瑨,刘飞扬,高 妍
(辽宁工程技术大学电气与控制工程学院,葫芦岛 125105)
随着一次能源的日益短缺,光伏发电起到越来越重要的作用[1-2],但其输出电压较低。Boost 变换器具有升压作用,因此被广泛应用于光伏发电,但是传统Boost 变换器对电压增益的提高能力有限,开关管电压应力也比较大。文献[3-4]提出一种交错并联Boost 变换器,电压增益提高较多,且开关管应力电压较小,但是对电流纹波没有进一步分析;文献[5]引入了开关电容网络,DCM 单元并联个数增多,电压增益线性提高,但是随着并联DCM 单元的增加,使得电路和控制方法都比较复杂;文献[6-7]提出了磁集成的设计准则以及气隙磁路的研究,为本文的磁集成提供理论依据;文献[8-9]提出了多输入直流变换器,提高效率;文献[10]提出一种隔离型交错并联耦合电感高增益Boost 变换器,降低开关管应力,但体积比较大,在许多场合应用受到限制。
针对光伏发电系统中对高增益输出的需求[11-12],本文提出基于倍压单元的高增益变换器,元器件数量少,电压增益得到很大提高,开关管应力电压得到很好改善,且将2 个独立电感耦合磁集成,有效减小了电感电流纹波。耦合电感的设计方案是全正向耦合,经仿真和实验可得该变换器性能优异,具有实际应用价值。
1 变换器的拓扑结构及工作原理
1.1 拓扑结构
具有倍压单元的磁集成Boost 变换器如图1 所示,倍压单元由电容C1、C2和二极管D1、D2、D3组成,电感L1、L2正向耦合。输入电压为6 V,L1=L2=50 μH,C0=C1=C2=20 μF,所有器件均为理想状态,开关管占空比为D。
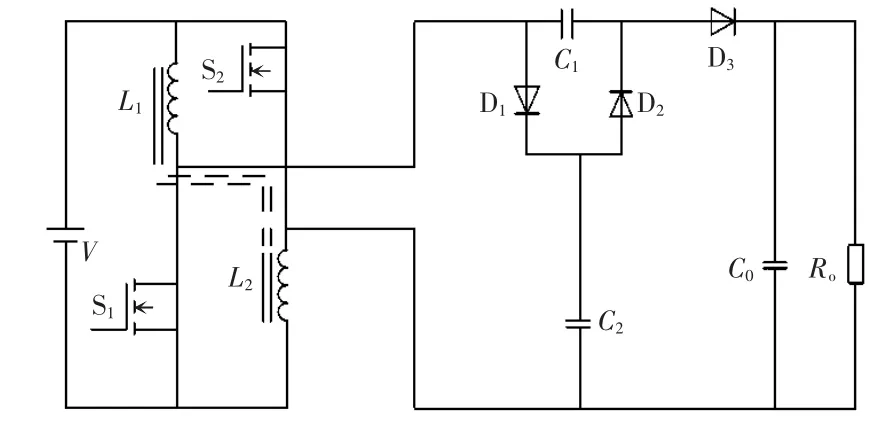
图1 基于倍压单元耦合电感高增益直流变换器Fig.1 Coupling inductor high-gain DC/DC converter based on voltage doubling unit
1.2 工作模态
在一个开关周期T 内,存在2 种工作模态。对应的开关管和二极管状态如表1 所示,变换器的主要工作波形以及开关模态的等效电路分别如图2和图3 所示。
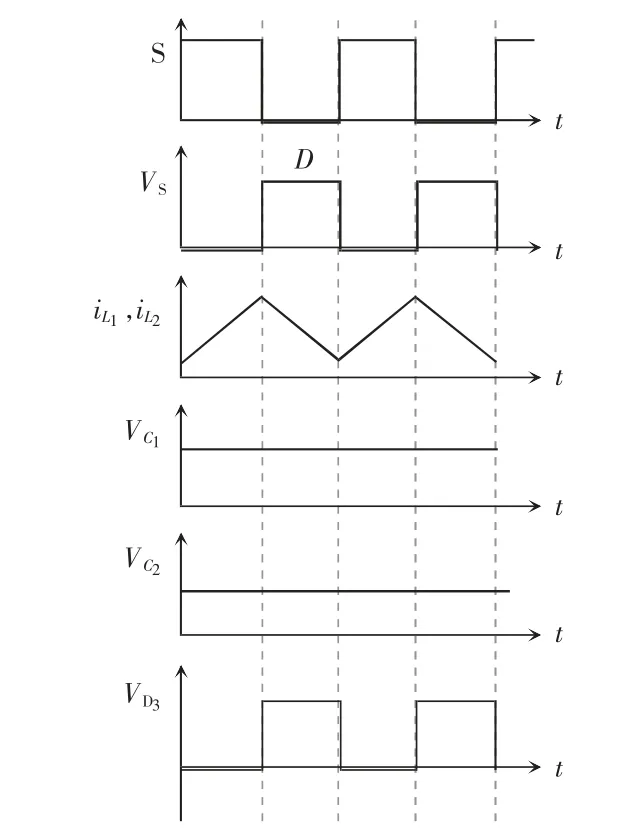
图2 变换器的主要工作波形Fig.2 Key working waveforms of converter

图3 不同模态的等效电路Fig.3 Equivalent circuits in different modes
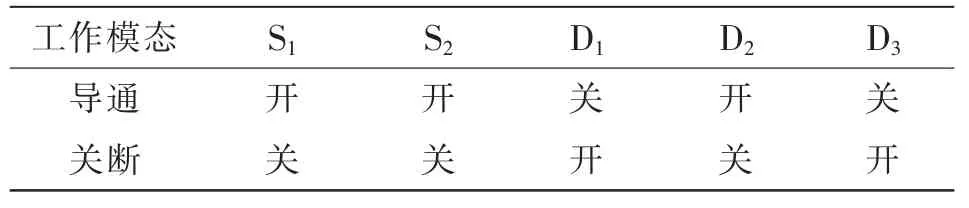
表1 开关管和二极管状态Tab.1 States of switch tubes and diodes
模态Ⅰ:开关管S1和S2同时开通。L1、L2和后级电路关系相同,故变化量相同,此时2 个电感同时充电,电源和C2共同给C1充电,其充电回路为V-S2-C2-D2-C1-S1,C1的电位为右正左负,电容C0给负载Ro供电。
模态Ⅰ的电路表达式为
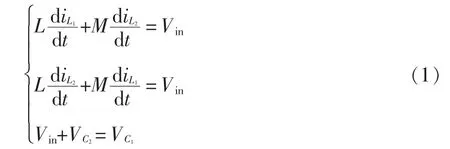
式中:L 为自感系数;M 为互感系数;iL1和iL2分别为电感L1和L2的电流Vin为输入电压;VC1和VC2分别为电容C1和C2的两端电压。
模态Ⅱ:S1和S2关断。电源和L1、L2及C1一起给负载供电并同时给C2充电。C2充电回路为V-L1-D1-C2-L2,C2的电位为上正下负,负载Ro的供电回路为V-L1-C1-D3-Ro-L2。
模态Ⅱ的电路表达式为
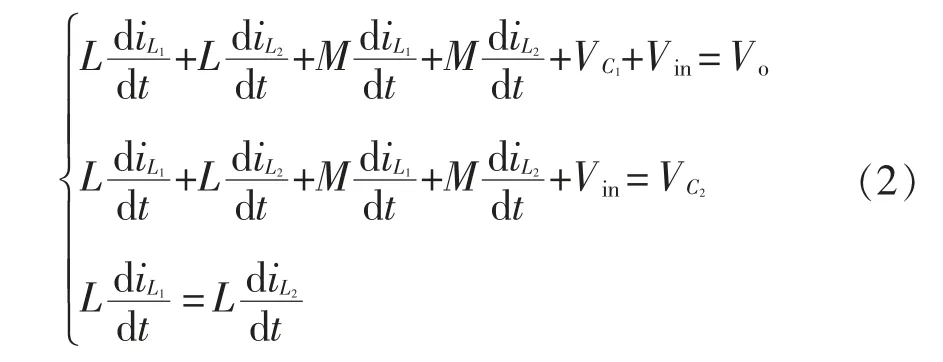
式中,Vo为输出电压。
2 变换器的性能分析
2.1 稳态电压增益
电感L1和L2的变化量相同,此处L=L1=L2,根据式(1)和式(2)可得电感电流变化量为
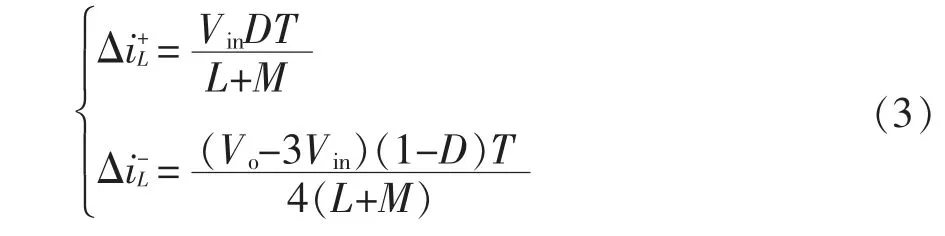
根据电感电流伏秒平衡定理可得,变换器的电压增益表达式为

2.2 变换器的电感电流纹波分析
独立电感时电感电流纹波为

对电感进行耦合集成,正向耦合的互感为M,此处L=L1=L2,耦合后电感电流纹波为

设耦合系数为K,则

由式(6)和式(7)可得

理想情况下K 达到1,此时电流纹波为

可见,电感电流纹波减小约一半。
2.3 开关管电压应力
开关管开通时应力为0,根据电路拓扑和模态分析,二极管和开关管的电压应力分别为
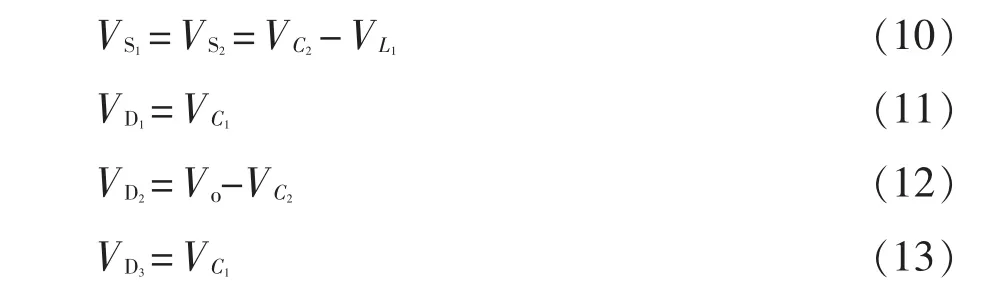
式中,VS1、VS2和VD1、VD2分别为S1、S2和D1、D2的电压应力。
以具体实例对本文变换器和传统Boost 变换器进行对比分析。当输入电压都为6 V、输出电压达到24 V 时,传统Boost 变换器开关管应力为24 V,本文变换器开关管应力电压为8 V,可见,对比传统Boost 变换器,在开关管应力方面得到明显改善。另外,当占空比取0.85 时,输出电压为150 V,开关管电压应力约为40.5 V。当电压增益很大时,开关管应力得到很好地限制,即本文提出的变换器适合应用于电压较高的场合。
3 集成磁件设计
本文采用“EE”型对电感耦合,电感L1和L2缠绕方式如图4 所示。“EE”型电感具有许多优点,如耦合系数调节方便简单、耦合度高等。
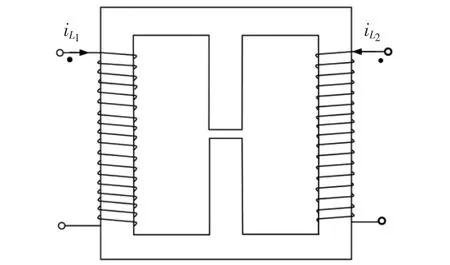
图4 耦合电感的结构Fig.4 Structure of coupling inductor
3.1 耦合电感磁路分析
文献[11]分析了带有气隙的磁路电感,电感自感计算公式为

式中:N 为电感L1和L2的匝数;R 为磁阻。
当磁芯气隙为δ 时,磁阻R 表示为

正向耦合时,互感M 为

L1=L2时,耦合系数K 为

电感L1和L2完全正向耦合,即耦合系数无限接近1。
3.2 拓扑延伸
把独立电感换成开关电感,增益会进一步提高,如图5 所示,模态分析与独立电感相同。列写电压增益公式为

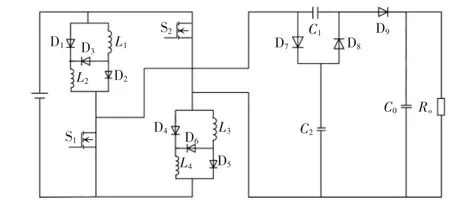
图5 基于开关电感倍压单元耦合电感高增益直流变换器Fig.5 Coupling inductor high-gain DC/DC converter based on switching inductor and voltage doubling unit
4 仿真与实验验证
4.1 仿真验证
用PSIM 仿真软件进行仿真验证。元器件参数分别为:Vin=6 V,电感L1=L2=20 μH,耦合系数K=0.96,电容C1=C2=20 μF,负载电阻Ro=40 Ω,电容C0=100 μF,开关频率为f=50 kHz。
图6 和图7 分别为当占空比为0.5 时传统Boost 变换器和本文变换器的输出电压仿真波形,分别为12 V 和40 V,与文中电压增益公式相对应。
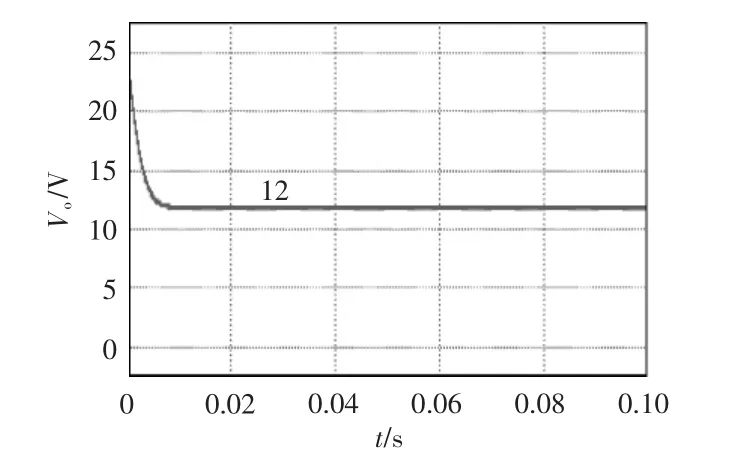
图6 传统Boost 变换器输出电压仿真波形Fig.6 Simulation waveform of output voltage from the traditional Boost converter
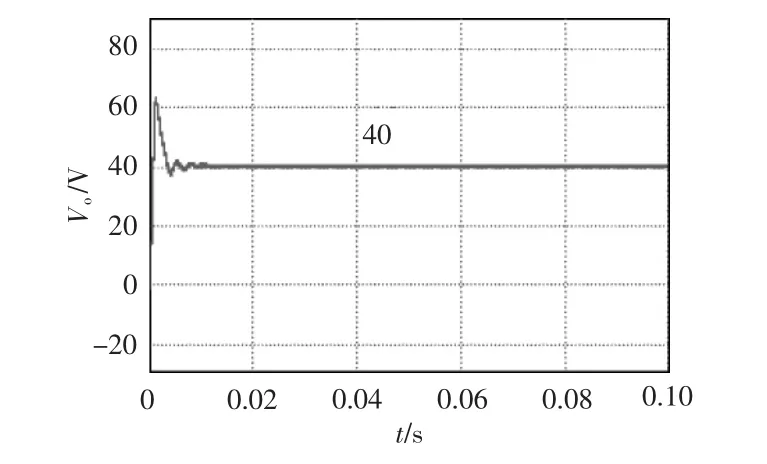
图7 本文变换器输出电压仿真波形Fig.7 Simulation waveform of output voltage from the proposed converter
图8 是独立电感和耦合后电感电流纹波,可见约减小一半。图9 为当占空比为0.75 时换开关电感前后输出电压波形,电压增益与文中公式对应。图10 为占空比为0.85 时输出电压Vo和VvpsS的仿真波形。
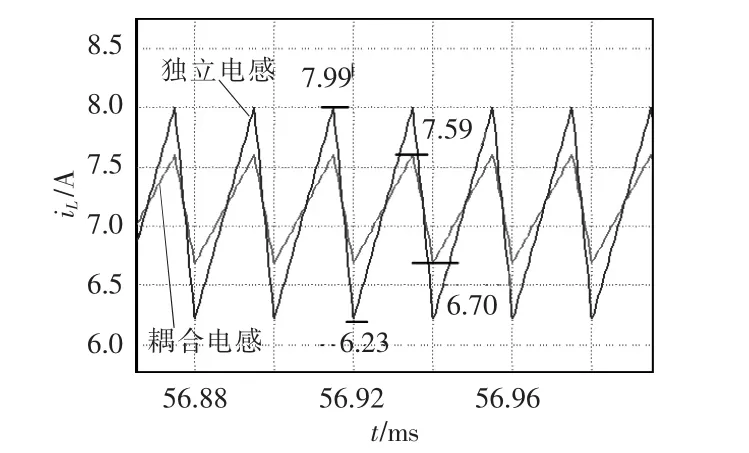
图8 耦合前、后电感电流纹波仿真波形Fig.8 Simulation wave form of inductor current ripple before and after coupling
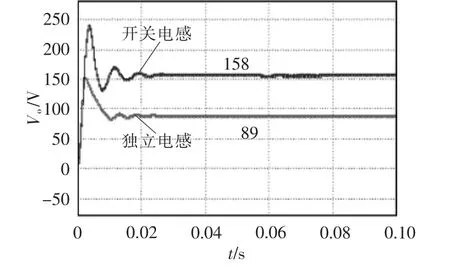
图9 占空比为0.75 时带有开关电感和独立电感的输出电压仿真波形Fig.9 Simulation wave form of output voltage with switching inductor and independent inductor at duty ratio of 0.75
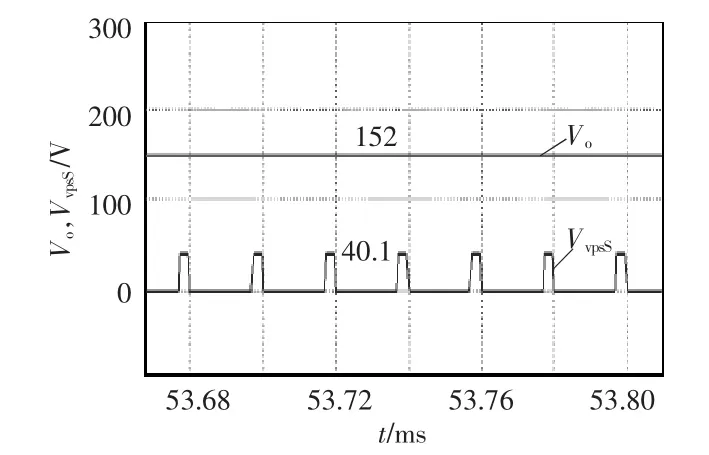
图10 占空比为0.85 时输出电压Vo 和开关管电压应力VvpsS 的仿真波形Fig.10 Simulation wave form of output voltage Vo and switching tube voltage stress VvpsS at duty ratio of 0.85
4.2 实验验证
为了验证理论分析的正确性,设计一台变换器原理样机。样机参数设置为:输入电压Vin=6 V,电容C1=C2=20 μF,C0足够大,开关频率f=50 kHz,正向耦合系数为0.96。表2 是耦合电感实验数据。

表2 耦合电感实验数据Tab.2 Experimental data of coupling inductor
经过实验所得的波形如图11~图13 可见,图11 中实验所测的输出电压Vo约为41 V,计算所得的理论值为42 V。由图12 和图13 可见,独立电感的电流纹波值约为1.76 A;对开关电感中的2 个电感进行耦合,耦合电感电流纹波值约为0.89 A,大约减小一半。以上数据与理论分析基本一致,验证了理论分析的正确性。
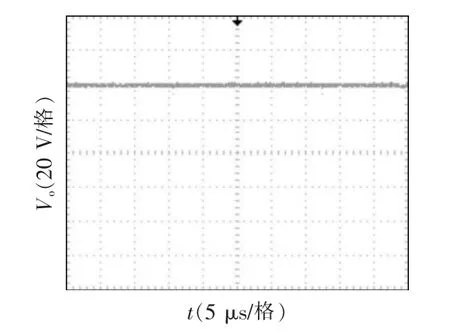
图11 输出电压Vo 的实验波形Fig.11 Experiment waveform of output voltage Vo
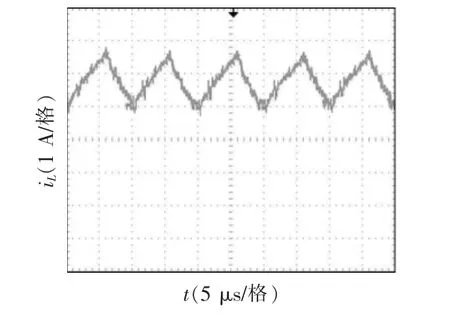
图12 独立电感电流实验波形Fig.12 Experiment waveform of independent inductor current
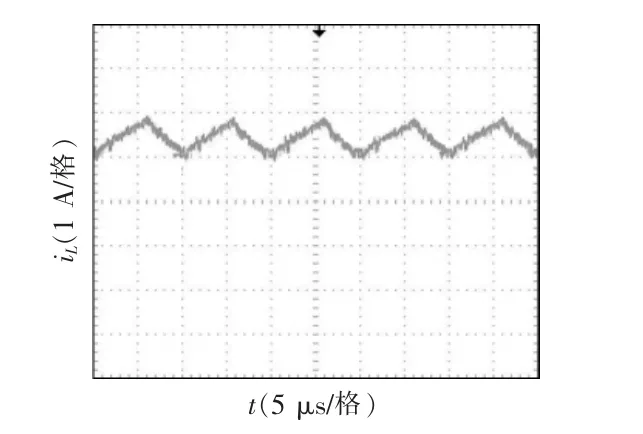
图13 耦合电感电流实验波形Fig.13 Experiment waveform of coupling inductor current
5 结论
本文提出一种基于倍压单元耦合电感高增益直流变换器,具有以下优点:
(1)电压增益得到明显提高;
(2)变换器电感电流纹波显著减小;
(3)当增益很大时,开关管应力电压减小明显。
