考虑通航环境因素的智能船舶航线规划
2021-10-08潘伟董其林许小卫何平谢新连
潘伟 董其林 许小卫 何平 谢新连


摘要:为提升智能船舶航线自动设计方案的合理性,考虑船舶通航环境因素的影响,提出一种考虑水深、潮高、风、浪、流的智能船舶航线规划算法。基于Delaunay三角剖分算法,提出一种环境建模方法,利用船舶航行安全水深理论在环境模型中搜索禁航区。利用切线图法建立可航网络。基于船舶力学原理对船舶干扰力进行建模,提出一种在环境干扰力影响下的可航网络权值修正方法。将提出的智能船舶航线规划算法用于对浙江舟山衢山岛北部水域的实例分析。仿真结果表明,该算法能够为不同环境下的不同尺度船舶规划出合适的航线,也能够为相同船舶给出适应不同环境的规划结果,从而证明该算法的有效性。
关键词: 智能船舶; 航线规划; 环境因素; Delaunay三角剖分; 切线图法
中图分类号: U675.79
文献标志码: A
收稿日期: 2020-11-13
修回日期: 2021-02-03
基金项目:
国家重点研发计划(2017YFC0805309);中央高校基本科研業务费专项资金(3132019303)
作者简介:
潘伟(1992—),男,辽宁大连人,博士研究生,研究方向为交通运输规划与管理,(E-mail)panweidlmu@163.com;
董其林(1972—),男,黑龙江哈尔滨人,高级工程师,研究方向为航务管理、自动化,(E-mail)498790034@qq.com
*通信联系人。(E-mail)xxlian@dlmu.edu.cn
Route planning of intelligent ships considering
navigation environment factors
PAN Wei1, DONG Qilin2, XU Xiaowei1, HE Ping1, XIE Xinlian1*
(1.Integrated Transport Institute, Dalian Maritime University, Dalian 116026, Liaoning, China;
2.Heilongjiang Provincial Waterway Affairs Center, Harbin 150026, China)
Abstract: The algorithm is able to give suitable routes for different-scale ships in different environments, and to prove the effectiveness of the algorithm.
To improve the rationality of intelligent ship route automatic design scheme, considering the influence of ship navigation environment factors, a ship route planning algorithm considering water depth, tide height, wind, wave and current is proposed. Based on Delaunay triangulation algorithm, a method of environment modeling is proposed, and the theory of safe water depth of ship navigation is used to search the restricted area in the environment model.The tangent graph method is used to establish the navigable network.Based on the principle of ship mechanics, the ship interference force is modeled, and a method of the weight correction of navigable network under the environmental interference force is proposed.The intelligent ship route planning algorithm is applied to the northern waters of Qushan Island of Zhoushan in Zhejiang province for example analysis. The simulation results show that the algorithm can provide suitable routes for ships with different sizes in different environments, and give planning results suitable for different environments for the same ship, which proves the effectiveness of the proposed algorithm.
Key words: intelligent ship; route planning; environmental factor; Delaunay triangulation; tangent graph method
0 引 言
船舶在航行过程中的航线规划受到各种环境因素的影响,是船舶安全、经济运行的基础。随着无人船技术的兴起,船舶自动航线设计也成为其核心技术之一。电子海图及相关助航设备已普及,通航环境参数和船舶航行信息的数字化技术已发展成熟。在智能船舶航线规划算法中,充分考虑环境因素,利用数字化技术及设备进行航线辅助设计,将是智能船舶进行合理航线规划的基本保障。因此,考虑通航环境因素的智能船舶航线规划算法研究具有十分重要的意义。
近年来,船舶航线规划算法的研究不断吸取其他领域在路径规划上的成功经验,逐渐发展成为路径规划算法的一个重要分支,取得了较为丰硕的研究成果。张立华等[1]考虑航行水域的水深和碍航物,提出一种基于电子海图的自动航线设计方法;李源惠等[2]利用电子海图信息,提出基于动态网格模型的航线规划算法;TAM等[3]结合交通流数据及环境数据,提出一种考虑船舶会遇状态的航线规划算法;曹鸿博等[4]对复杂情形下的航线规划算法进行优化,提出改进的最短距离航线自动生成算法;NAEEM等[5]考虑《国际海上避碰规则》,
提出一种无人船避碰路径规划算法;庄佳园等[6]提出一种基于航海雷达的水面无人艇局部路径规划算法;王涛等[7]考虑船舶转向限制,提出一种最短距离航线自动生成算法;向哲等[8]利用海量AIS数据,提取出船舶习惯航路并应用于船舶航线规划;
XU等[9]考虑环境因素影响,提出一种开阔海域的船舶航线规划算法;谢新连等[10]考虑船舶在绕开碍航区时的避碰问题,提出一种复杂水域船舶避碰路径规划算法;SHEN等[11]将粒子群优化算法(particle swarm optimization, PSO)与切线图法相结合来搜索最优船舶航线;XIE等[12-13]提出改进的多方向A*算法,解决了海上风电场水域的船舶路径规划问题;GKEREKOS等[14]提出了一个基于船舶性能和气象条件的航线规划框架;WEN等[15]将DBSCAN(density-based spatial clustering of applications with noise)与人工神经网络相结合,实现了基于港口间AIS数据的船舶航线自动设计;CHEN等[16]提出一种基于Q学习的路径规划方法,能夠让船舶按照该路径规划结果进行自主航行。
从已有的研究可以发现,船舶航线规划算法可以分为解析法和智能法。解析法着眼于船舶实际的航行环境和气象环境,通过对环境进行建模,进而获得船舶可航水域,完成船舶航线规划设计;智能法主要对船舶航迹、船舶航行参数等大量相关历史数据进行挖掘、分析和学习,进而通过智能算法求解可靠的经验路线。这都为船舶航线自主设计的研究提供了坚实的基础。然而,针对不同尺度、不同类型的船舶,环境模型通常采用通用模型,难以满足实际应用过程中的航行安全要求;此外,在考虑环境因素影响的算法中,对多种环境因素的综合考虑还不充分,并且没有考虑潮高值对环境建模的影响。
虽然在求解船舶航线规划问题时,采用解析法和智能法均可以获得较好的效果,但是在处理绕开临时禁航区时,解析法能够直接将环境数据、气象数据作为参数代入算法进行航线求解。因此,本文提出一种基于解析法的航线规划算法。首先提出一种综合考虑船体参数、水深、潮高值的环境建模算法,
用于自动提取船舶禁航区域,并根据实时潮高值和船舶吃水需要给出适应的环境模型;再利用基于船舶参数的航速修正算法对环境模型进行权值修正,通过模型求解为船舶规划出既安全又高效的航线。
1 基于电子海图数据的航行水域环境建模
电子海图将真实水域资料以数据的形式进行保存和显示,其中水域水深数据以〈坐标,水深值〉的形式存储在电子海图文件中,并能够以离散点的形式在电子海图中显示。Delaunay三角剖分算法是广泛应用于数值分析(比如有限元分析)以及图形学的一项重要预处理技术。
1.1 电子海图数据的Delaunay三角剖分算法
电子海图的水深数据集合K可以表示为{kii=1,2,…,n},其中ki的数据结构为〈(xi,yi),hi〉,(xi,yi)为坐标点,hi为该点水深值。
Delaunay三角剖分算法能够根据离散的坐标数据构建该区域的Delaunay三角网模型,该模型可以表示为集合{tjtj∈M,j=1,2,…,m},tj的数据结构为〈l1,l2,l3〉,其中li的数据结构为〈k(i)0,k(i)1〉。根据文献[17-19]的比较分析结果,采用Marcum提出的基于Delaunay空洞性质的增量法[20]对电子海图水深数据进行三角模型化处理,仅保留水深数据。其算法伪代码如下:
输入{kiki∈K,i=1,2,…,n}
输出{tjtj∈M,j=1,2,…,m}
1创建包含集合K所有元素的初始三角形t0
2创建拆分三角形集合S′
3创建重构边集合L,集合元素个数g
4将t0加入集合M,m=1
5for i=1 to n do
6 for j=1 to m do
7 if ki在tj的外接圆内
8 将tj从M中删除并加入S′
9 end if
10 end for
11 删除S′中元素的公共边,其余边加入L
12 for u=1 to g do
13 用ki和lu构建新三角形tm+1,加入M
14 end for
15end for
16for j=1 to m do
17 if tj表达的是陆地
18 将tj从M中删除
19 end if
20end for
1.2 搜索禁航区范围
碍航区除了陆地、岛屿外,水深不满足船舶吃水要求的区域同样为碍航区域。为保证船舶航行安全,应选择水深超过船舶吃水并留有一定安全余量的水域航行[21]。
HS=HC+HT≥HA+dm
(1)
式中:HS为船舶航行安全水深;HA为最小安全富余水深;dm为船舶吃水;HC为电子海图水深(该点理论最低潮面的水深);HT为潮高。对于船舶富余水深,文献[21]给出了不同机构对船舶富余水深的规定,综合考虑船舶安全等因素,取船舶吃水的10%作为最小安全富余水深,式(1)可以转化为
HS=HC+HT≥dm×110%
(2)
利用船舶航行安全水深HS,在Delaunay电子海图模型中进行搜索,获得不满足船舶航行安全水深的区域边界,构建禁航区。采用式(3)利用等深线li的两端点坐标(x1,y1)和(x2,y2)求取安全水深的区域边界点坐标(xS,yS),这里k1的数据结构为〈(x1,y1),h1〉,k2的数据结构为〈(x2,y2),h2〉。
xS=x1+(HS-h1)(x2-x1)h2-h1
yS=y1+(HS-h1)(y2-y1)h2-h1
(3)
等深線搜索算法伪代码如下,其中RS为等深线集合:
输入{tjtj∈M,j=1,2,…,m}
输出{lili∈RS,i=1,2,…,n}
1for j=1 to m do
2 if HS-htj(l1)、HS-htj(l2)、HS-htj(l3)异号(htj(lx)为三角形tj的顶点水深数值,x=1,2,3)
3 利用式(3)求解等深线端点坐标
4 求取等深线li,加入集合RS
5 end if
6end for
遍历等深线集合RS,通过首尾连接构建碍航区边界,创建碍航区集合{(o,β)i(o,β)i∈O,i=1,2,…,n},二元组(o,β)元素包含碍航区边界数据o和边界个数β。
1.3 可航水域无向图构建
已知碍航区集合后,无法直接进行船舶航线设计,需要将碍航区转化为可航水域无向图,英国学者DOYLE等[22]提出了机器人在二维平面上构建无向网络的切线图法,并证明最短路径是由凸多边形边界与凸多边形间的公切线组成的。在通过等深线搜索获得的Delaunay电子海图模型中,碍航区形状不全为凸多边形,可采用顶角判别算法进行处理。可航水域无向图的构建步骤如下:
步骤1 遍历碍航物集合{(o,β)i(o,β)i∈O,i=1,2,…,n},对各碍航区顶点进行校验,若其夹角小于90°则保留顶点,若其夹角大于等于90°,则删除该顶点,获得处理后的碍航区集合{(o,β)i(o,β)i∈Onew,i=1,2,…,n
}。
步骤2 输入起点和终点,校验起点和终点是否包含在碍航区内。
步骤3 创建集合O*,连接起点与终点生成探测线,将探测线经过的碍航区加入集合O*;循环遍历集合O*,以经过起点的碍航区切线、经过终点的碍航区切线作为新的探测线,将经过的碍航区加入集合O*,未穿越的探测线加入集合P,直至集合O*在新一轮遍历中不再添加新的碍航区。
步骤4 遍历集合O*,求任意两碍航区的公切线段,以公切线段为探测线,将探测线经过的碍航区加入集合O*,未穿越的探测线加入集合P,直至集合O*在新一轮遍历中不再添加新的碍航区。
步骤5 获得无向图网络边界集合{pjpj∈P,j=1,2,…,m}。
2 环境因素对航速影响的量化分析
量化环境因素的影响是实现航线设计的重要前提。在影响船舶航速的众多因素中,风、浪、流影响较大也较容易被量化[23]。将环境因素的量化结果与船舶力学原理相结合,计算在环境因素影响下的船舶航速。利用航速对可航水域无向图进行权值修正,将环境因素的影响加入船舶航线设计中。
2.1 船舶阻力模型
在静水中航行时,船舶在推力T的作用下克服总阻力Rt前进。这里,推力T可以通过主机有效功率计算,总阻力Rt可以通过估算公式[24]进行计算:
Rt=12ρSCtv2
(4)
式中:S为船舶湿表面面积,可采用文献[24]的估算图谱进行估算;Ct为总阻力系数;ρ为水域水密度;v为船舶航行的速度。
Ct=Cf+Cr+ΔCAR
(5)
式中:Cf为摩擦阻力系数,可采用桑海公式[25]估算;Cr为剩余阻力系数,可以采用Lap-Keller图谱进行估算;
ΔCAR为粗糙度补贴系数[26-27]。
2.2 环境干扰力模型
2.2.1 风对船体的作用力
船舶航行时,水线面以上部分受到风的作用力Fwind,沿艏艉方向的分力为Fwind,x,横向分力为Fwind,y:
Fwind,x=12ρaAfv2windCwind,x(αR)
Fwind,y=12ρaAsv2windCwind,y(αR)
(6)
式中:ρa为空气密度;Af和As分别为水线面以上的正投影面积和侧投影面积;vwind为相对风速;αR为风舷角;Cwind,x(αR)和Cwind,y(αR)分别为纵向和横向风压力系数,其值可按文献[28]的经验公式求取。
2.2.2 浪对船体的作用力
水面波浪会对船体形成作用力Fwave,沿艏艉方向的分力为Fwave,x,横向分力为Fwave,y:
Fwave,x=12ρgLoaξ2Cwave,xcos(π-θwave+ψ)
Fwave,y=12ρgLoaξ2Cwave,ysin(π-θwave+ψ)
(7)
式中:ρ为水的密度;g为重力加速度;Loa为船长;ξ为平均波浪幅值;Cwave,x和Cwave,y分别为纵向和横向波浪漂移力系数,其值可按文献[28]的回归公式求取;θwave为波向;ψ为艏向。
2.2.3 流速与航速的矢量运算
船舶在水面航行时相对水面的速度为v,水流速度为vC,流向为ψC,船舶对地航速为vR。其关系如图1所示。
2.3 航行环境中的船体力学模型
考虑船舶航行时的推力、阻力、环境干扰力以及水流对航速的影响,对船体进行受力分析,再利用水流流速修正船舶对地航速。为求得船舶在环境因素影响下的实际航速,仅需考虑附体坐标系中x方向的受力,如图2所示,图中ψwind为风向角。
船体受力模型为
T=Rt+Fwind,x+Fwave,x
(8)
3 航线规划流程及求解方法
3.1 航线规划流程
考虑到环境因素对船舶航速的影响,距离最短的航线规划结果并不一定满足航行时间最短。本文提出的船舶航线规划算法包括环境建模和航线求解两个部分。环境建模采用电子海图数据进行Delaunay电子海图建模,利用船舶航行需要的安全水深进行碍航区搜索,利用切线图法在碍航区建立可航水域无向图。航线求解部分考虑环境因素对航速的影响进行无向图权值修正,再通过Dijkstra算法进行求解,便可求得航行时间最短的航线。航线规划流程见图3。
3.2 求解方法
利用环境参数、船舶参数综合求解出船舶航速,利用船舶航速修正可航网络权重,求解后即可获得考虑环境因素的航线。
3.2.1 构建船舶总阻力与航速图谱
根据式(8)可知,船舶在推力恒定时,航速只受环境因素的影响,在可航水域内非匀速运动。
由式(4)和式(5)可知,无法直接求解式(8)获得船舶航速,因此需要采用间接的方式求解。当船舶不受环境干扰时,满足
T=Rt
(9)
根据第2.1节可知,船舶总阻力可利用由船舶参数构建的函数表达式进行求解,其隐式表达式为
Rt=f(ρ,S,v,Loa,ν,AM,Cp)
(10)
式中:ν为流体运动黏性系数;AM为中剖面面积;Cp为棱形系数。上式中航速v为变量,其余船舶参数为常量,故设航速计算精度为Δv,在航速区间(0,vmax)内计算式(10)的值,获得以Rt为自变量,v为因变量的关系图谱。
3.2.2 环境干扰力求解
对通航水域采用墨卡托坐标以精度μ(精度μ的取值根据环境数据的精度确定)划分网格,根据网格的行列数,构建对应的环境数据矩阵D,矩阵元素((vwind,ψwind),(ξ,θwave),(vC,ψC))对应一个单元网格的环境数据,包括风、浪、流的速度值与方向。
网格区域中的航迹(如航迹A、B、C)如图4a所示,其中航迹经过的单元网格采用灰色底纹表示,航迹被网格划分为不同长度的子段(每个灰色单元网格包含一个子段)。
为降低计算难度,以航迹B为例对环境干扰力的求解方法进行简化。航迹B的航向角为ψB,在x轴方向,将航迹按照网格线划分为长度相等的子段(长度为μ/sin(ψB-0.5π),首尾子段B1、B9除外,见图4b),存在子段经过1个单元网格(如B3经过单元网格4,记为情况1)和同时经过2个连续单元网格(如B2连续经过单元网格2和3,记为情况2)的情况,处理方法如下:(1)在情况1下,直接利用该单元网格的数据矩阵进行环境干扰力
(Fwind,x,Fwave,x)求取。(2)在情况2下,如图4b所示,将2个单元网格融合,并采用如下方式进行数据处理:①当两个单元网格对应的矩阵元素完全相同时,直接利用相同的矩阵元素进行计算。②当两个单元网格对应的矩阵元素存在不同时,求取融合后的数据,再用该数据进行计算。假定子段中点坐标为
(x0,y0),两个单元网格的共线的y轴坐标为ymid,两个单元网格的数据分别为ui和ui+1,则融合后的网格对应的矩阵元素各个值用unew表示,其计算公式(当两个单元网格为横向排列时,式中y坐标值均改用x坐标值进行计算)为
unew=
(0.5μ+y0-ymid)ui+(0.5μ-y0+ymid)ui+1μ
(11)
航迹C是一种较特殊的情况,航迹与两个相邻单元网格的公共边(如单元网格1与2、单元网格3与4、单元网格5与6的公共边)重合。航迹C的环境数据计算是子段同时经过2个连续单元网格的特殊情况,航迹向为90°与270°时同理。
若在x轴方向上细分航迹A,则会出现一条子段穿过3个连续单元网格的情况(如单元网格12、13和14);若在y轴方向上细分航迹A,就可以避免这个问题,并且可以采用处理航迹B时的融合算法。令ψ为航迹向。若0≤ψ≤π/4或3π/4≤ψ≤5π/4或7π/4≤ψ<2π,则在y轴方向分段;若π/4<ψ<3π/4或5π/4<ψ<7π/4,則在x轴方向分段。
3.2.3 环境干扰下的无向图权值修正
航迹子段的环境干扰力(Fwind,x,Fwave,x)计算完成后,将结果代入式(8)求得船舶总阻力,结合第3.2.1节生成的船舶总阻力和航速图谱,求得船舶在各子段航行的航速
vi,获得航速集合{vii=1,2,…,p},p为子段数量。根据第2.2.3节的结论,求得各子段对应的水流速度纵向分量
{vC,x,ii∈1,2,…,p}。
航迹子段长度集合为{wii=1,2,…,p},在各子段对应的航行时间集合为
{titi=wi/(vi+vC,x,i),i∈1,2,…,p}。将该航迹的路径权值由距离权重转化为时间权重:
t=pi=1ti
(12)
4 算例分析
采用4艘不同尺度的船进行算例分析。利用4艘船的参数,分别进行环境建模,验证算法对不同尺度船舶的适用性;对同一艘船在不同潮高条件下进行计算,验证算法能否在不同潮高条件下为船舶提供安全的航行路线;采用同一船型进行距离最短航线规划与时间最短航线规划比较。利用浙江舟山衢山岛北部水域作为实验水域进行算例分析,该水域内岛屿分布较为密集,水深允许中小型船舶通航。
4.1 算例数据
实验所用船舶参数见表1。
采用表3提供的船舶参数,计算各船的总阻力,绘制总阻力与航速图谱,见图5。
环境数据采用第10届国际拖曳试验水池会议(ITTC)提出的15 ℃淡水密度999.04 kg/m3;空气密度取1.29 kg/m3,潮高值取小衢山岛附近(岱山)的潮汐表数据,见图6。
4.2 结果与分析
4.2.1 潮高因素影响分析
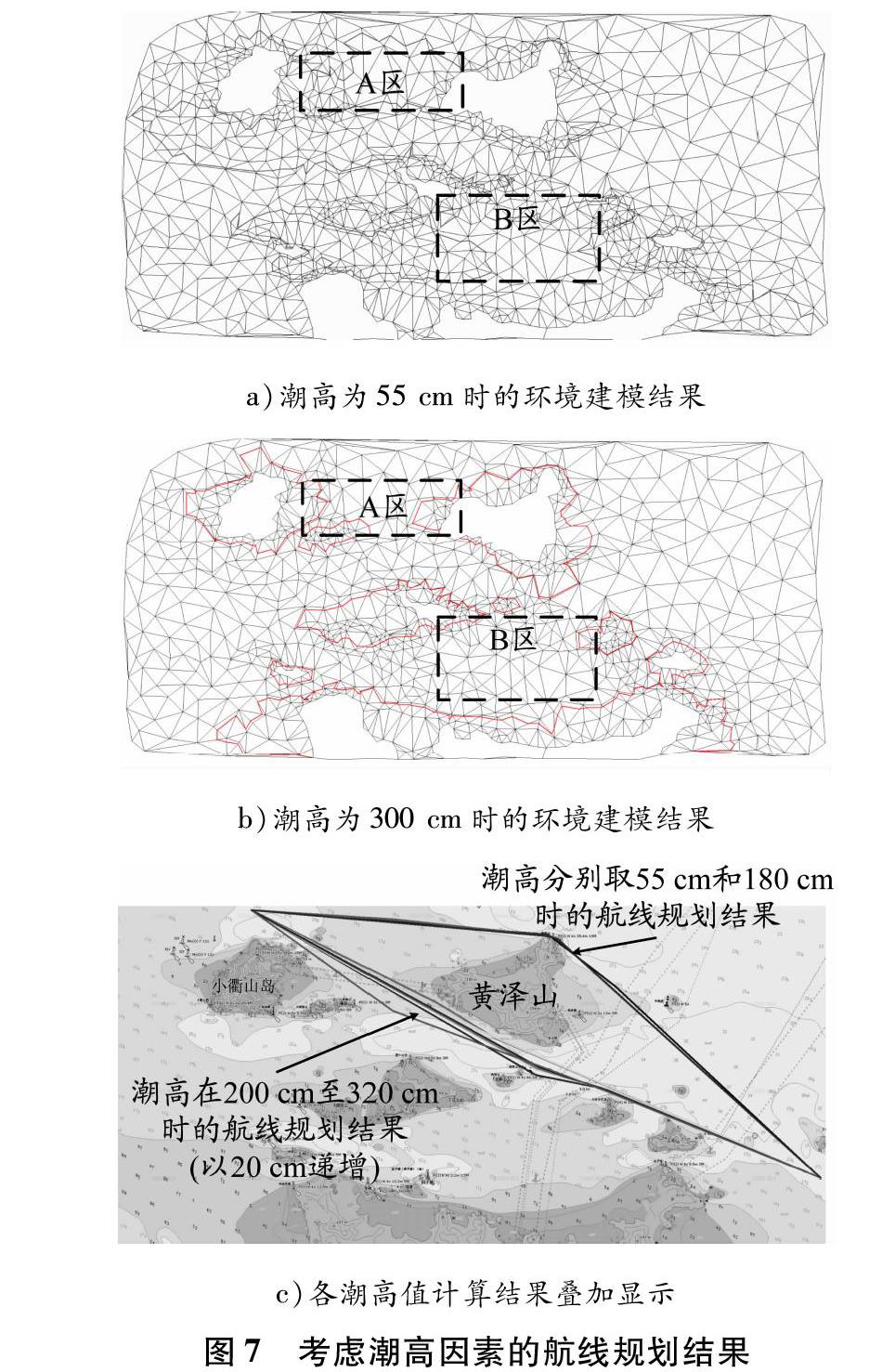
由图6可知,航行水域的潮高在不同时间有不同的取值,导致船舶安全航行水域范围不同。因此,为验证潮高对船舶航线规划的影响,对船1进行不同潮高条件下的航线规划,结果见图7。
当气象数据采用固定值时,将不同潮高水位与电子海图水深叠加后,实验水域水深在不同潮高条件下有较大的差异,图7a和7b分别展示了潮高分别为55 cm和300 cm时的环境建模结果。这2个模型的差异在于可航水域不同,其中的A区与B区在不同潮高条件下可航性不同。以B区为例,在潮高为55 cm时,B区水域为不可航行水域;当潮高为300 cm时,B区为可航行水域。
环境建模后,利用切线图法构建可航网络无向图,并采用Dijkstra算法对无向图进行求解。环境模型的差别导致为相同船舶规划的航线存在一定的差异(潮高取55 cm以及从60 cm升至320 cm,以20 cm递增)。由计算结果可知,潮高在55 cm至200 cm时,船舶无法在小衢山岛与黄泽山之间的水域航行(即A区),必须从黄泽山北部水域通过(仅保留潮高取55 cm和180 cm的航线规划结果,见图7c);而潮高在200 cm至320 cm时,A区水域水深满足实验船航行安全水深,规划的航线经过该水域。实验结果证明:考虑潮高因素的算法具有很好的适用性。
4.2.2 Delaunay环境模型比较分析
根据式(2)可知,4艘船的航行安全水深分别为3.96、7.70、11.55和15.18 m。对Delaunay电子海图模型进行碍航区搜索:设定相同的起点和终点,采用固定的潮高值和气象数据,利用提出的算法进行计算,结果见图8。
由图8可知,Delaunay环境模型能够将水深数据通过三角网格模型进行表达,不同尺度船舶具有不同的航行安全水深。以此在Delaunay环境模型中进行碍航区搜寻,可以获得不同尺度船舶的碍航区数据。算法为不同尺度船舶规划出了符合其航行安全水深要求的航线,验证了该算法对不同吃水船舶的适用性。
4.2.3 环境干扰力影响分析
本文提出的算法主要针对短程航线设计,与传统的气象导航不同,可以忽略环境数据在短时间内的变化,为智能船舶提供考虑环境因素的局部航线规划方案。因此,设置特定的气象数据(风向与流向相同),如图9a所示,并且风力恒定,流速恒定,波向及幅值恒定。
对船1分别进行距离最短航线规划(实验1)和时间最短航线规划(实验2),实验变量控制见表2。实验结果见图9b。2条航线比较见表3。
由表2可知,两次实验的控制变量为气象因素。由表3可知,与距离最短航线相比,时间最短航线的航行距离增加2.16%,航行时间节约9.15%,平均航速增加12.46%。
综上分析,在考虑环境因素影响后,船舶的航行状态受环境因素影响产生了较大的变化(航速增幅超过10%)。在实际航行中,气象因素的影响是难以避免的,本文提出的船舶航线规划算法在处理气象因素影响时表现出较好的优势,能够有效地帮助船舶规划出更加适应实际需要的航线。
5 结束语
随著海上智能交通和智能船舶的快速发展,考虑环境因素影响的船舶航线规划算法具有广泛的应用前景。本文提出了一种考虑环境因素的船舶航线规划算法,能够综合考虑水深、潮汐、风、浪和流对船舶航行的影响,并通过解析法进行求解。
在船舶航线设计过程中,充分考虑多种因素对船舶航线设计的影响,结果表明:提出的算法能够针对不同尺度船舶建立适当的环境模型,并能够将环境对船舶航行的影响进行量化计算,使航线规划结果无须进行大量人工修正,从而提高航线设计工作的自动化程度。
随着无人船的兴起,作为实现无人船自主航行的核心技术之一,考虑环境因素的智能船舶航线规划算法将有更加广阔的应用前景。本文提出的算法也可以帮助船舶驾驶员进行航线设计,大幅降低航线设计的人工成本,提高航线质量,保障船舶航行安全、经济。在未来的研究中,水上施工区域、军事演习区域等人工划定禁航区域的处理将加入到算法的环境建模部分,以进一步提高算法的自动处理性能。
参考文献:
[1]张立华, 朱庆, 刘雁春, 等. 电子海图平台下的航线自动设计方法[J]. 大连海事大学学报, 2007, 33(3): 109-112. DOI: 10.3969/j.issn.1006-7736.2007.03.024.
[2]李源惠, 潘明陽, 吴娴. 基于动态网格模型的航线自动生成算法[J]. 交通运输工程学报, 2007, 7(3): 34-39. DOI: 10.3321/j.issn:1671-1637.2007.03.008.
[3]TAM C K, BUCKNALL R. Path-planning algorithm for ships in close-range encounters[J]. Journal of Marine Science and Technology, 2010, 15(4): 395-407. DOI: 10.1007/s00773-010-0094-x.
[4]曹鸿博, 张立华, 贾帅东, 等. 电子海图最短距离航线自动生成的改进方法[J]. 武汉大学学报(信息科学版), 2011, 36(9): 1107-1110. DOI: 0.13203/j.whugis2011.09.003.
[5]NAEEM W, IRWIN G W, YANG Aolei. COLREGs-based collision avoidance strategies for unmanned surface vehicles[J]. Mechatronics, 2012, 22(6): 669-678. DOI: 10.1016/j.mechatronics.2011.09.012.
[6]庄佳园, 苏玉民, 廖煜雷, 等. 基于航海雷达的水面无人艇局部路径规划[J]. 上海交通大学学报, 2012, 46(9): 1371-1375.
[7]王涛, 张立华, 彭认灿, 等. 考虑转向限制的电子海图最短距离航线自动生成方法[J]. 哈尔滨工程大学学报, 2016, 37(7): 923-929. DOI: 10.11990/jheu.201503059.
[8]向哲, 施朝健, 胡勤友, 等. 一种利用海量AIS数据规划安全航线的方法[J]. 中国安全生产科学技术, 2016, 12(10): 160-164. DOI: 10.11731/j.issn.1673-193x.2016.10.027.
[9]XU Wen, HU Jiangqiang, YIN Jianchuan, et al. Ship automatic collision avoidance by altering course based on ship dynamic domain[C]//2016 IEEE TrustCom-BigDataSE-ISPA. IEEE, 2016.
[10]谢新连, 何平, 何傲, 等. 复杂水域船舶避碰路径规划研究[J]. 重庆交通大学学报(自然科学版), 2019, 38(12): 1-7. DOI: 10.3969/j.issn.1674-0696.2019.
[11]SHEN Yu, WANG Fuping, ZHAO Peimin, et al. Ship route planning based on particle swarm optimization[C]//2019 34th Youth Academic Annual Conference of Chinese Association of Automation (YAC). IEEE, 2019: 211-215.
[12]XIE Lei, XUE Shuangfei, ZHANG Jinfen, et al. A path planning approach based on multi-direction A* algorithm for ships navigating within wind farm waters[J]. Ocean Engineering, 2019, 184: 311-322. DOI: 10.1016/j.oceaneng.2019.04.055.
[13]ZHA Tianqi, XIE Lei, CHANG Jiliang. Wind farm water area path planning algorithm based on A* and reinforcement learning[C]//2019 5th International Conference on Transportation Information and Safety (ICTIS). IEEE, 2019: 1314-1318.
[14]GKEREKOS C, LAZAKIS I. A novel, data-driven heuristic framework for vessel weather routing[J]. Ocean Engineering, 2020,
197: 106887. DOI: 10.1016/j.oceaneng.2019: 106887.
[15]WEN Yuanqiao, SUI Zhongyi, ZHOU Chunhui, et al. Automatic ship route design between two ports: a data-driven method[J]. Applied Ocean Research, 2020: 102049. DOI: 10.1016/j.apor.2019.102049.
[16]CHEN Chen, CHEN Xianqiao, MA Feng, et al. A knowledge-free path planning approach for smart ships based on reinforcement learning[J]. Ocean Engineering, 2019: 106299. DOI: 10.1016/j.oceaneng.2019.106299.
[17]张尧, 樊红, 黄旺. 基于Delaunay三角网的等高线树生成方法[J]. 测绘学报, 2012, 41(3): 461-467.
[18]武晓波, 王世新, 肖春生. Delaunay三角网的生成算法研究[J]. 测绘学报, 1999, 28(1): 28-35.
[19]杨钦. 限定Delaunay三角网格剖分技术[M]. 北京: 电子工业出版社, 2005: 53-67.
[20]MARCUM D L, WEATHERILL N P. Unstructured grid generation using iterative point insertion and local reconnection[J]. AIAA Journal, 1995, 33(9): 1619-1625. DOI: 10.2514/3.12701.
[21]王鹤荀, 郭洪驹. 船舶安全富余水深的确定[J]. 上海海事大学学报, 2004, 25(4): 19-21. DOI: 10.3969/j.issn.1006-1738.2004.05.001.
[22]DOYLE A B, JONES D I. A tangent based method for robot path planning[C]//IEEE International Conference on Robotics & Automation. IEEE, 1994: 1561.
[23]魏照坤, 谢新连, 魏明. 风浪影响下的集装箱班轮航速优化[J]. 交通运输系统工程与信息, 2016, 16(3): 154-160. DOI: 10.16097/j.cnki.1009-6744.2016.03.023.
[24]贾欣乐, 杨盐生. 船舶运动数学模型: 機理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999: 150-152.
[25]盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2004: 164-166.
[26]应业炬. 船舶快速性[M]. 北京: 海军出版社, 2017: 27-29.
[27]刘桂杰, 郭春雨, 李茂华, 等. 船舶阻力图谱计算与模型试验结果比较分析[J]. 中国舰船研究, 2014, 9(3): 38-42. DOI: 10.3969/j.issn.1673-3185.2014.03.005.
[28]乐美龙. 船舶操纵性预报与港航操纵运动仿真[M]. 上海: 上海交通大学出版社, 2003: 6-13.
(编辑 赵勉)
