考虑碳排放成本的长江铁矿石运输研究
2021-10-08赵晓胡鸿韬
赵晓 胡鸿韬
摘要:为降低钢铁企业采购和运输铁矿石的综合成本,考虑船型、航速和碳排放等因素,建立长江铁矿石运输的混合整数非线性规划模型。将模型中的非线性项转化为线性项,运用CPLEX求解器求解。针对CPLEX求解中大型规模算例的局限性,引入标准粒子群优化(particle swarm optimization, PSO)算法提高求解精度。针对标准PSO算法容易陷入局部最优的问题,提出一种基于自适应策略的改进PSO算法,动态调整惯性权重,提高算法的收敛性和全局寻优能力。通过数值实验发现,改进后的算法在全局寻优能力和收敛能力上有一定的提高。
关键词: 多层级运输网络; 碳排放; 混合整数非线性规划; 粒子群优化(PSO)算法
中图分类号: U695.2
文献标志码: A
收稿日期: 2021-03-29
修回日期: 2021-04-26
基金项目: 国家自然科学基金(71771143)
作者简介:
赵晓(1996—),男,四川巴中人,硕士研究生,研究方向为内河航运,(E-mail)1515992779@qq.com;
胡鸿韬(1981—),男,四川绵阳人,教授,博导,博士,研究方向為港口和航运管理与优化、供应链网络设计与优化,(E-mail)hthu@shmtu.edu.cn
Meeting of the Waterborne Transport Division, World Transport Convention 2021 (WTC 2021)
Research on iron ore transportation in the Yangtze River considering carbon emission cost
ZHAO Xiaoa, HU Hongtaob
(a. Institute of Logistics Science & Engineering; b. Logistics Engineering College, Shanghai Maritime University, Shanghai 201306, China)
Abstract: In order to reduce the overall cost of steel companies purchasing and transporting iron ore, taking into account factors such as ship type, navigation speed and carbon emission, a mixed-integer nonlinear programming model of iron ore transportation in the Yangtze River is established. In the model, the nonlinear terms are converted into the linear terms, and the CPLEX solver is used to solve the model. Aiming at the limitation of CPLEX in solving medium and large scale cases, the standard particle swarm optimization (PSO) algorithm is used to improve the accuracy of solutions. For the problem that the standard PSO algorithm is easy to fall into the local optimum, an improved PSO algorithm based on adaptive strategy is proposed, which can dynamically adjust the inertia weight to improve the algorithms convergence and global optimization ability. Through numerical experiments, it is found that the improved algorithm has a certain improvement in the global optimization ability and convergence ability.
Key words: multi-level transportation network; carbon emission; mixed-integer nonlinear programming; particle swarm optimization (PSO) algorithm
0 引 言
近年来,以长江为纽带的城市在快速发展的同时也带动了长江航道的进一步发展。这些长江沿岸城市建有许多钢铁厂,需要通过长江航道来运输冶炼钢铁所需的铁矿石。从国外采购铁矿石再运输至国内,涉及采购价格、船型、航速等问题,因此本文研究在铁矿石的采购和运输过程中,如何合理选择铁矿石供应商、安排船型、制定航速以及考虑绿色内河航运因素,将总成本降到最低。
为实现更高质量的绿色内河航运,在考虑碳税政策和碳排放的前提下,林贵华等[1]针对航速优化、航线配船、货物分配问题,建立了船公司收益最大化的混合整数非线性模型。隋志超等[2]认为征收碳税和实施碳排放交易机制是实现碳减排目标的有效手段。李晗[3]把政府征收的碳税作为班轮公司碳减排行为的主要影响因素,并建立了考虑碳排放的集装箱班轮航线配船优化模型。吕靖等[4]认定征收碳税会增加集装箱班轮公司的运营成本。李旭等[5]认为在引入碳税政策后,需要综合考虑单路径碳排放约束、整个海运网络碳排放约束和不同地区碳税差异。苗红云等[6]以航道和港口设计通过能力为条件,将碳排放转化为低碳成本,并考虑减载运输来建立内河散货运输网络优化模型,并通过算例分析证明了该模型可以有效降低运输中的碳排放。
在研究内河运输时,学者们发现内河运输的总成本不仅包含运营成本、碳排放成本,还包括装卸成本、码头停靠成本等。LI等[7]选取长江沿岸的钢铁企业为对象,研究如何使企业运营成本最低,而YANG等[8]通过优化模型让总运输成本与未满足所有需求的罚款的总和达到最小。ZHENG等[9]研究了集装箱运输轴辐式网络设计,并提出一个最小混合整数线性规划模型。YANG等[10]建立了以成本最低为目标的长江集装箱班轮运输网络优化模型。KONNINGS等[11]探讨了鹿特丹港集装箱驳船装卸作业的改进方法以达到成本最低的目标。MENG等[12]所提出的轴辐式网络以最小化承运商的总运输成本和枢纽运营商的运营成本为目标。MOON等[13]提出一个在轴辐式网络中船队部署的最小不定期船航线模型。而在内河航运的服务研究中,TAN等[14]针对船舶排程设计和航行速度最佳化问题,建立了成本最小化双目标规划模型。
本文在以往研究的基础上,考虑船舶运输铁矿石的周期、运输铁矿石所使用船舶的类型以及船舶在通过不同航段时的航速、碳排放成本等因素,以钢铁企业的铁矿石采购和运输总成本最低为目标建立混合整数非线性规划模型。将模型中的非线性项转化为线性项,引入标准粒子群优化(particle swarm optimization, PSO)算法提高求解精度。提出一种基于自适应策略的改进PSO算法,使模型更容易实现、求解精度更高、收敛速度更快。
1 问题描述和模型
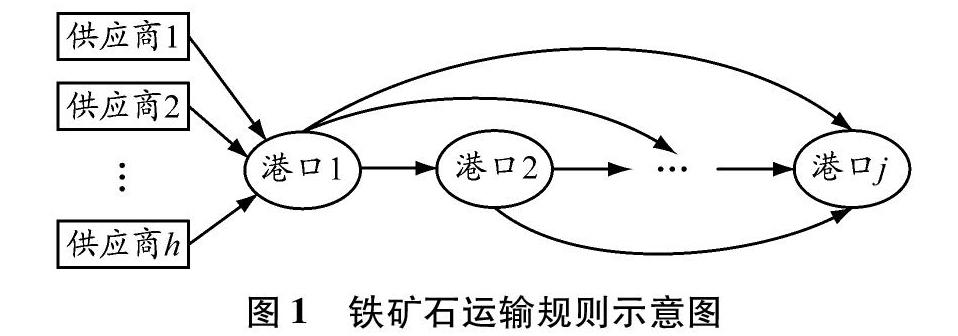
一家位于长江边的钢铁企业在计划周期t内将从国外供应商处购买的铁矿石通过船舶运输到国内指定港口进行卸船和转运(见图1)。铁矿石不能直接从供应商处运输至转运港口之外的其他港口,因为受其他港口的水深限制,铁矿石需先在规定的转运港进行卸船并装载到载重较小的船舶上,然后运输至长江沿岸上游其他港口。考虑不同类型船舶的载重,决策各航段运输所需使用船舶的类型及数量。以钢铁企业总运营成本为目标函数,并同时考虑与船舶航速、船舶载重等因素相关的碳排放成本。
本文所考虑的长江内河散货运输问题,不仅要考虑相应参数的动态性、不同类型船舶的载重量、船舶航速、碳排放成本等相关因素,而且要满足每个接收铁矿石的港口对铁矿石的需求,决策每个周期内需从供应商处采购的铁矿石数量、各接收铁矿石的港口之间需运输铁矿石的数量和运输铁矿石所需的船舶数量。
1.1 条件假设
已知所選定钢铁企业的船舶资源及相关航线信息,针对案例提出以下6点假设:(1)因为本文涉及小规模算例,其周期不会太长(不超过一个月),且通常散货船的租金一般以日为单位进行收取,所以本文周期以日为单位[15];(2)港口根据其实际地理位置排序;(3)铁矿石只能从下游港口运输至上游各港口,不能从上游港口运输至下游各港口;(4)每个港口的需求是预先设定的,而且必须得到满足;(5)船舶的靠港时间和在各港口的装卸作业时间以及由此所产生的成本归入船舶运输铁矿石的时间和成本中;(6)运输铁矿石的船舶都为满载状态。
1.2 模型建立
1.2.1 参数与变量
参数:t为周期,t=1,2,…,T;v为船型,v=1,2,…,V;s为航速,s=1,2,…,S;h为供应商,h=1,2,…,H;j为中转港,j=1,2,…,N-1;k为目的港,k=j+1;Qv为船型为v的船舶容量大小;ths为船舶以航速s从供应商h到港口1的运输时间;pht为在周期为t时从供应商h处采购铁矿石的单价;chvst为在周期为t时船型为v的船舶以航速s从供应商h到港口1的满载运输成本;rhvst为在周期为t时船型为v的船舶以航速s从供应商h到港口1的满载碳排放成本;Ik0为在周期开始时港口k的库存;Ikt为在周期t末港口k的剩余库存;dkt为在周期为t时港口k对铁矿石的需求量;lkt为在周期为t时港口k对铁矿石的单位存储成本;tjks为船舶以航速s从港口j到港口k的运输时间;cjkvst为在周期为t时船型为v的船舶以航速s从港口j到港口k的满载运输成本;rjkvst为在周期为t时船型为v的船舶以航速s从港口j到港口k的满载碳排放成本;M表示足够大的正数。
决策变量:xhvt,在周期为t时船型为v的船舶从供应商h到港口1的铁矿石运输数量;yhvst,在周期为t时以航速s从供应商h到港口1运输铁矿石所需的船型为v的船舶的数量;xjkvt,在周期为t时船型为v的船舶从港口j到港口k的铁矿石运输数量;yjkvst,在周期为t时以航速s从港口j到港口k运输铁矿石所需的船型为v的船舶的数量;zhvst是0-1变量,若在周期为t时船型为v的船舶以航速s从供应商h运输铁矿石到港口1,则其值为1,否则为0;zjkvst是0-1变量,若在周期为t时船型为v的船舶以航速s从港口j运输铁矿石到港口k,则其值为1,否则为0;Yhvst与Zjkvst是辅助决策变量,其值均大于0。
1.2.2 总成本最小化模型
本文所建立的总成本最小化模型为混合整数非线性规划(mixed-integer nonlinear programming, MINLP)模型:
minHh=1Vv=1Tt=1phtxhvt+Hh=1Vv=1Ss=1Tt=1chvstyhvstzhvst+
N-1j=1Nk=j+1Vv=1Ss=1Tt=1cjkvstyjkvstzjkvst+
Hh=1Vv=1Ss=1Tt=1rhvstyhvstzhvst+
N-1j=1Nk=j+1Vv=1Ss=1Tt=1rjkvstyjkvstzjkvst+Nk=1Tt=1Iktlkt
(1)
s. t.
Hh=1Vv=1t-thsτ=1xhvτ+I0=
tτ=1d1τ+It+Nk=2Vv=1tτ=1x1kvτ
(2)
k-1j=1Vv=1t-tjksτ=1xjkvτ+Ik0=
tτ=1dkτ+Ikt+Nj=k+1Vv=1tτ=1xkjvτ
(3)
yhvstQv≥xhvt
(4)
yjkvstQv≥xjkvt
(5)
Vv=1Ss=1zhvst=1
(6)
Vv=1Ss=1zjkvst=1
(7)
xhvt,yhvst,xjkvt,yjkvst,Ikt≥0
(8)
zhvst,zjkvst∈{0,1}
(9)
式(1)為目标函数,其第一项为从供应商处采购铁矿石的成本,第二项为从供应商处运输铁矿石到第一个港口的运输成本,第三项为在各港口之间运输铁矿石的运输成本,第四项为从供应商处运输铁矿石到第一个港口的碳排放成本,第五项为在各港口之间运输铁矿石的碳排放成本,最后一项为铁矿石在港口的仓储成本;式(2)和(3)分别为铁矿石从供应商处向港口1运输和铁矿石在各港口之间运输的流平衡;式(4)和(5)分别为铁矿石从供应商处向港口1运输和铁矿石在各港口之间运输时的船舶数量限制;式(6)和(7)分别为铁矿石从供应商处向港口1运输和铁矿石在各港口之间运输时船型和航速的决策;式(8)为非负变量的数值定义;式(9)为0-1变量的数值定义。
1.3 模型线性化
本文模型中包含了决策船型和航速,因此目标函数中存在非线性项。为便于求解,引入两个辅助决策变量将目标函数中的非线性项转化为线性项,改进后的模型如下:
minHh=1Vv=1Tt=1phtxhvt+Hh=1Vv=1Ss=1Tt=1chvstYhvst+
N-1j=1Nk=j+1Vv=1Ss=1Tt=1cjkvstZjkvst+Hh=1Vv=1Ss=1Tt=1rhvstYhvst+
N-1j=1Nk=j+1Vv=1Ss=1Tt=1rjkvstZjkvst+Nk=1Tt=1Iktlkt
(10)
s. t.
式(2)~(9)
Yhvst≥(zhvst-1)M+yhvst(11)
Zjkvst≥(zjkvst-1)M+yjkvst(12)
改进后的模型比原模型多了两个约束(式(11)和(12))。这两个约束建立起两个相乘的决策变量之间的线性关系,从而将模型转化为CPLEX能够求解的一般线性规划模型。
1.4 参数设置
本文研究的问题是从钢铁企业的角度需要解决的问题。实验所使用的不同规模的数据是通过查阅相关航运资料、宝钢钢铁企业相关资料并结合实际设置的,不同规模下的集合数据见表1。模型中的其他参数是通过利用程序代码在合理且符合实际的范围下随机产生的,数据如下:(1)运输铁矿石的各类船舶的容量在[2,20]万t内离散均匀产生;(2)从供应商处到港口1的运输时间为其距离与航速的比值;(3)各供应商的铁矿石价格在[500,900]元/t内随机产生;(4)根据相关资料,铁矿石运输成本c与船舶容量Qv、船舶航速s、船舶运价p1、运价转化系数p2存在关系c=p1Qv+p2(s+10),其中船舶在从供应商处到港口1和从港口1到其他港口的运价p1分别在[50,100]元/t和[20,50]元/t内随机产生,船舶在从供应商处到港口1和从港口1到其他港口的运价转换系数p2分别在[10,30]和[10,15]内随机产生;(5)根据相关资料,碳排放成本r与船舶容量Qv、船舶航速s、单位碳排放成本k1、碳排放成本转化系数存在关系r=k1Qv+k2(s+10),其中k1在[200,400]元/t内随机产生,k2在[30,50]内随机产生;(6)港口铁矿石周期初、末的库存均在[1 000,4 000]t内均匀产生;(7)每个港口的铁矿石需求在[0.5,2]万t内随机产生;(8)每个港口的铁矿石仓储成本在[1,7]元/t内随机产生;(9)从港口1到其他港口的运输时间为其距离与航速的比值。
2 求解算法
2.1 PSO算法
PSO算法首先对粒子进行初始化,每个粒子代表一个解。在一个B维搜索空间有n个粒子,粒子i(i=1,2,…,n)的位置和速度分别为xi和vi。在每次迭代中,粒子通过跟踪两个极值pi和gi来更新自己,这里,pi和gi分别为个体极值和全局极值。在找到这两个最优值后,粒子更新自己的速度和位置的方法如下:
vi=wvi+c1ri(pi-xi)+c2ri(gi-xi)(13)
xi=xi+vi(14)
式中:w为惯性权重,w∈[0.4,0.9],w值越大,说明粒子全局寻优能力越强,局部寻优能力越弱;ri为(0,1)内的随机数;c1和c2为学习因子,通常c1=c2=2。粒子速度的最大值用vmax表示,如果粒子速度超过vmax,则取vi=vmax。
2.2 改进的PSO算法
在PSO算法中,权重w对全局寻优和局部寻优有着很大的影响,因此选择合适的w是提高算法寻优能力的关键。为提高PSO算法的收敛性以及避免PSO算法陷入局部最优,引入自适应权重[15](权重w随着每个粒子的位置、速度的更新进行自适应调整)。本文w取值与当前迭代次数d和迭代总次数D有关。
通过自适应调整权重w的PSO算法更新公式如下:
wid=wmin+(wmax-wmin)f(xid)-fdminfdavg-fdmindD,
f(xid)≤fdavg
wmax, f(xid)>fdavg
(15)
式中:wmin和wmax为预设的最小速度权重和最大速度权重,一般取wmin=0.4,wmax=0.9;f(xid)为粒子i第d次迭代时的适应度值;fdavg为第d次迭代时所有粒子的平均适应度值;fdmin为所有粒子第d次迭代时的最小适应度值,fdmin=min{f(x1d),f(x2d),…,f(xnd)}。适应度值越小,说明距离最优解越近,此时更需要局部搜索;适应度值越大,说明距离最优解越远,此时更需要全局搜索。
改进的PSO算法流程见图2。
2.3 算法求解过程
粒子群中每个粒子代表一个解,因为粒子是随机生成的,所以可以保证粒子的多样性。选取0-1变量zhvst和zjkvst进行编码,共生成kt个zhvst和k(k-1)t/2个zjkvst作为生成的初始粒子群,经过算法迭代得到种群中最优的港口k和周期t所代表的位置,最后获得粒子的最优位置和目标函数值。
算法中每个粒子的解P包含整数部分和小数部分,P的取值范围为[0,vs-1]。由P/S得到的整数代表zhvst的v;P/S的余数代表zhvst中的s,其小数部分如在[0,0.5]范围内则向下取整,如大于0.5则向上取整。在j、k、t、h分别确定的情况下,唯一的v、s也就随之确定。
3 算 例
3.1 3种规模算例实验
本次算例实验平台的CPU为Intel Core i5-9400 2.9 GHz,运行内存为8 GB,Windows 10 64位处理系统。采用Python 3.7进行编程,线性规划求解部分调用CPLEX 12.6.2求解器进行求解。标准PSO算法参数如下:粒子群种群规模为100,迭代次数为50,权重w取wmin与wmax的均值0.6;改进PSO算法中权重w通过自适应进行调整,其余参数的设置与标准PSO算法的一致。本文设置的小规模、中規模、大规模算例分别包括3个港口、8个港口、20个港口,每个规模生成了12组数据。将每组数据输入模型中进行求解,求解时间及结果见表2~4。由表2可知,CPLEX的求解时间较短,说明在进行小规模算例求解时,采用CPLEX进行求解是最为合适的。随着算例规模的增大,CPLEX的求解时间也增加,当算例规模增大到一定程度时CPLEX无法在合适的时间内找出最优解,因此,中大规模算例已不适合用CPLEX进行求解。对于中大规模算例,标准PSO算法和改进的PSO算法均能在合适的时间范围内求解出对应的最优解,而且求解出的解的质量较好。相比之下,中规模算例采用改进的PSO算法的求解效果比大规模算例的好。
3.2 参数灵敏度分析
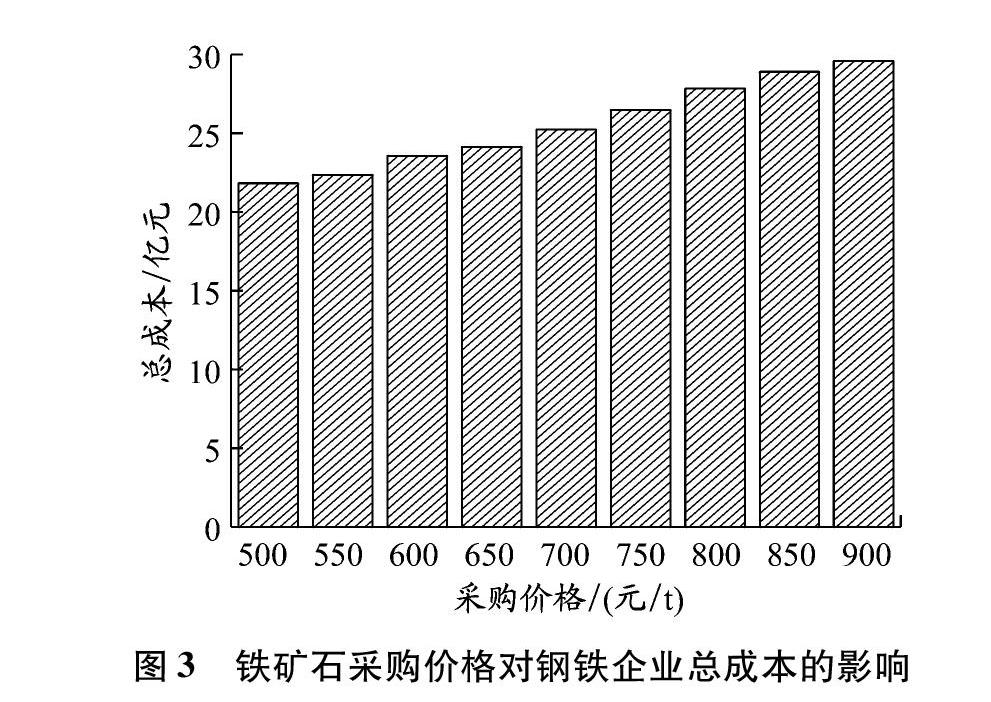
模型中涉及的一系列参数,例如铁矿石的采购价格、铁矿石的仓储成本等,分别分布在成本函数的各项成本中,其余参数均与之相关。下面对铁矿石采购价格进行灵敏度分析,假设铁矿石的供应商为3个,其分别位于澳大利亚、巴西、南非,且有载重量分别为60 000 t和80 000 t的两种灵便型散货船可供选择,航速可选择12 kn和15 kn。在其他参数都一样的情况下,改变铁矿石的采购价格,得到钢铁企业总成本的变化情况,见图3。
由图3可以看出,随着铁矿石采购价格的不断提高,钢铁企业的总成本也在相应增加。由此可见各国的铁矿石市场价格很大程度上也会影响钢铁企业的运营。模型中其他参数如各港口对铁矿石的需求、铁矿石的仓储成本等发生变化产生的影响均与铁矿石市场价格的影响一致,钢铁企业的总运营成本会随着这一系列参数的变化而发生改变。
3.3 算法迭代过程对比
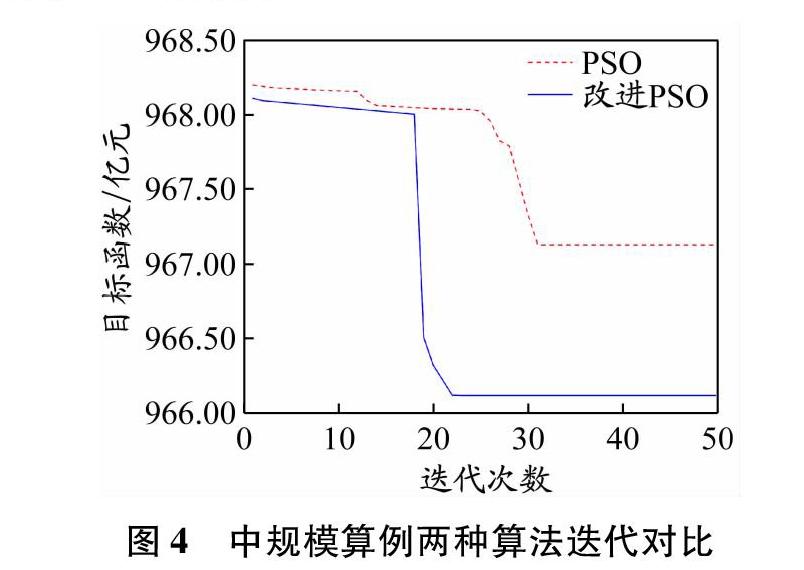
为验证本文所用算法的有效性,选取中规模、大规模算例进行实验,中(大)规模算例的相关参数设置:港口数为8(20)个、规划周期为30 d(80 d)、船型数为6种(15种)、航速为6 kn(15 kn)以及供应商数为6个(15个)。标准PSO算法和改进的PSO算法的迭代过程对比见图4和5。两种算法在求解过程中逐步寻优,并在经过不同的迭代次数后收敛于不同的稳定值。由图4和5可以知,两种算法求解时,虽然标准PSO算法的收敛速度快于改进的PSO算法,但是改进的PSO算法所得到的结果优于标准的PSO算法。
4 结 论
针对长江内河铁矿石运输问题,在考虑碳排放成本的情况下,以一家位于长江边的钢铁企业为研究背景,以钢铁企业的铁矿石采购和运输总成本最低为目标建立混合整数非线性规划模型。采用标准粒子群(PSO)算法和改进的PSO算法进行求解并评价两种算法的适用性。本文所提出的优化模型,能够让钢铁企业铁矿石的采购和运输总成本有明显降低,为钢铁企业运营决策提供一定的参考,如选择相对大的船型可以增加每艘船的铁矿石运输量,从而减少运输次数、降低运营成本。
参考文献:
[1]林贵华, 高洁, 李雨薇, 等. 考虑ECA和碳税政策的班轮航线及货物分配优化[J/OL]. 工业工程与管理: 1-12[2021-03-28]. http://kns.cnki.net/kcms/detail/31.1738.T.20200525.1834.012.html.
[2]隋志超, 吕靖. 碳税和碳排放交易机制对班轮船队经营的影响[J]. 中国水运, 2019, 19(2): 64-66.
[3]李晗. 考虑碳排放的集装箱班轮航线配船研究[D]. 大连: 大连海事大学, 2019.
[4]吕靖, 毛鹤达. 硫排放控制区和碳排放限制下的班轮航线配船模型[J]. 大连海事大学学报, 2017, 43(1): 101-105. DOI: 10.16411/j.cnki.issn1006-7736.2017.01.016.
[5]李旭, 孟燕萍. 碳税对集装箱海运网络运输成本的影响[J]. 上海海事大学学报, 2019, 40(2): 12-17. DOI: 10.13340/j.jsmu.2019.02.003.
[6]苗红云, 杨家其. 考虑低碳成本的内河散货运输航线网络优化模型[J]. 武汉理工大学学报(交通科学与工程版), 2017, 41(5): 839-843. DOI: 10.3963/j.issn.2095-3844.2017.05.025.
[7]LI Feng, YANG Dong, WANG Shuaian, et al. Ship routing and scheduling problem for steel plants cluster alongside the Yangtze River[J]. Transportation Research Part E, 2019, 122: 198-210. DOI: 10.1016/j.tre.2018.12.001.
[8]YANG Dong, WANG Shuaian. Analysis of the development potential of bulk shipping network on the Yangtze River[J]. Maritime Policy & Management, 2017, 44(4): 512-523. DOI: 10.1080/03088839.2016.1275863.
[9]ZHENG Jianfeng, YANG Dong. Hub-and-spoke network design for container shipping along the Yangtze River[J]. Journal of Transport Geography, 2016, 55: 51-57. DOI: 10.1016/j.jtrangeo.2016.07.001.
[10]YANG Zhongzhen, SHI Haiping, CHEN Kang, et al. Optimization of container liner network on the Yangtze River[J]. Maritime Policy & Management, 2014, 41(1): 79-96. DOI: 10.1080/03088839.2013.780217.
[11]KONNINGS R, KREUTZBERGER E, MARA V. Major considerations in developing a hub-and-spoke network to improve the cost performance of container barge transport in the hinterland: the case of the port of Rotterdam[J]. Journal of Transport Geography, 2013, 29: 63-73. DOI: 10.1016/j.jtrangeo.2012.12.015.
[12]MENG Qiang, WANG Xinchang. Intermodal hub-and-spoke network design: incorporating multiple stakeholders and multi-type containers[J]. Transportation Research Part B, 2011, 45: 724-742. DOI: 10.1016/j.trb.2010.11.002.
[13]MOON I K, QIU Z B, WANG J H. A combined tramp ship routing, fleet deployment, and network design problem[J]. Maritime Policy & Management, 2015, 42(1): 68-91. DOI: 10.1080/03088839.2013.865847.
[14]TAN Zhijia, WANG Yadong, MENG Qiang, et al. Joint ship schedule design and sailing speed optimization for a single inland shipping service with uncertain dam transit time[J]. Transportation Science, 2018, 52(6): 1297-1588. DOI: 10.1287/trsc.2017.0808.
[15]于桂芹, 李劉东, 袁永峰. 一种结合自适应惯性权重的混合粒子群算法[J]. 哈尔滨理工大学学报, 2016, 21(3): 49-53. DOI: 10.15938/j.jhust.2016.03.010.
(编辑 贾裙平)
