巴特沃斯低通滤波器在图像增强中的应用研究

肖锦龙

(东莞理工学校，广东 东莞523460)

0 引 言

改善图像质量是图像处理最基本目的之一，而图像增强是改善图像质量的最常用技术，因此图像增强在图像处理过程中有着很重要的地位和作用［1］。图像增强的目的就是为了使图像更加清晰，视觉效果更好，便于后期的图像分析和处理［2］。若按照图像在不同作用域中进行图像处理来分，可以分为空域内处理和频域内处理［3］。空域处理也叫时域处理，是直接对图像进行各种处理；而频域内处理是通过变换函数把图像转换为某个变换频域，再改变换频域对图像的变换系数进行运算处理，然后再通过变换函数的逆变换从而实现图像增强效果［4］。

随着图像处理技术的不断发展，不断涌现出各种新方法，目前在图像增强研究方面比较新的有模糊技术和小波变换等。图像增强技术方法众多，但每种方法都有各自的优缺点，因图像增强涉及的面比较广，因此没有一种方法可以完全取代其它方法，不同的图像对图像增强的要求不同，所采用的算法也不同。本文介绍的巴特沃斯低通滤波器图像增强属于频域滤波增强，其通过傅里叶变换把图像转换为频域，再进行巴特沃斯低通滤波，然后用傅里叶逆变换转换回空域，最终实现图像增强效果。

1 图像知识介绍

1.1 离散傅里叶变换

傅里叶变换被认为是描述图像信息的第二种语言，广泛应用于数字图像处理的频谱分析，是线性系统分析的一个非常有用的工具。傅里叶变换是数字图像处理技术的基础，其能在时空域和频率域中来回切换图像。普通的图像计算和处理都是很复杂的，但通过傅里叶变换后，再对图像信息特征进行提取和分析，计算工作量明显降低。因此在数字图像处理领域，起着非常重要的作用，常用于图像分析、图像增强和图像压缩等［5］。傅里叶变换包含连续傅里叶变换、离散傅里叶变换、快速傅里叶变换和短时傅里叶变换等，在数字图像处理使用的是二维离散傅里叶变换。

顾名思义，离散傅里叶变换就是傅里叶变换在时间和频率域上均以离散的形式存在。假设有离散序列f（x），其一维离散傅里叶变换定义为:

离散序列f（x）的长度为N，u＝0，1，…，N-1，则F(u)的一维离散傅里叶反变换可以定义为:

根据式（1）和式（2）离散傅里叶变换推广到二维时，则可以设离散函数f（x，y）。

其中，x＝0，1，…，M-1，y＝0，1，…，N-1。二维离散傅里叶变换定义为:

式中，u＝0，1，…，M-1，v＝0，1，…，N-1。F(u，v)二维离散傅里叶反变换可以定义为:

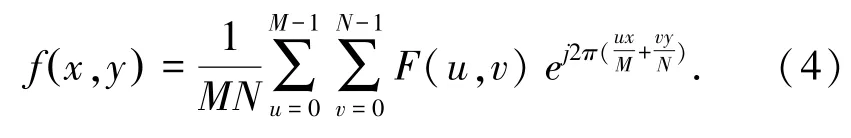
其中，x＝0，1，…，M-1；y＝0，1，…，N-1；u和v是频率变量。

1.2 图像增强

假设f（x，y）为原始图像函数，h（x，y）为滤波器函数。在空域内滤波的卷积运算，如式（5）所示:

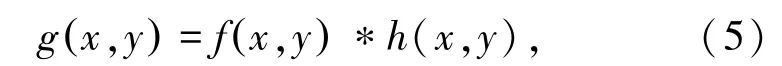
其中，函数h（x，y）可以是低通滤波，也可以是高通滤波，函数g(x，y)为空域滤波后输出的图像函数。根据卷积定理，式（5）的傅里叶变换可以表示如式（6）:

式（6）中，H（u，v）为滤波传递函数，可以根据不同的滤波要求进行设计，其与F(u，v)相乘，即可得到在频域内改善的频谱G(u，v)，从而实现在频域内的高低通或其它滤波。经过滤波后的频谱G(u，v)还要进行傅里叶反变换，最后得到滤波图像g(x，y)［6］。其中频域滤波的关键是G(u，v)函数的设计。

1.3 图像质量评价

图像质量评价方法分为2类，即主观评价和客观评价。主观评价方法是指通过人们观察来对图像质量的优劣做出判断，最具代表性的方法就是主观质量评分法。该方法预先指定测试的评价尺度，然后对测试图像按所看到的视觉效果给出图像等级。主观评价方法应该是最准确的、最能表示人们视觉感受的方法。但主观评价方法不够稳定，易受周围环境和个人情绪等因素影响。而且主观评价方法费时费力，在实际工程应用中比较难采用。客观评价方法是用处理图像与原始图像的误差来衡量处理图像的质量［7］。最具有代表性的方法评价指标有均方误差（MSEA）和峰值信噪比（PSNE）等。

2 巴特沃斯滤波器

巴特沃斯滤波器（Butterworth filter）被称作最大平坦滤波器，是连续衰减的滤波器，即巴特沃斯滤波器不会出现太大陡峭的变化。巴特沃斯滤波器的特点是在通频带内的频率响应曲线呈最大限度的平坦，没有纹波，而在阻频带内则逐渐下降为0［6］。巴特沃斯滤波器根据截至频率的不同分为低通滤波器、高通滤波器和带阻滤波器。

2.1 巴特沃斯低通滤波器

低通滤波的作用是让信号中的低频信息通过，而滤掉或抑制高频信息［7］，在实际中最重要的作用就是滤掉高频的噪声。图像中的噪声大部分集中在高频部分，所以低通滤波能平滑图像噪声。由于图像的边缘也集中在高频部分，所以在平滑噪声的同时也会平滑图像边缘，从而造成图像不同程度上的模糊。巴特沃斯低通滤波器的传递函数H（u，v）如式（7）:

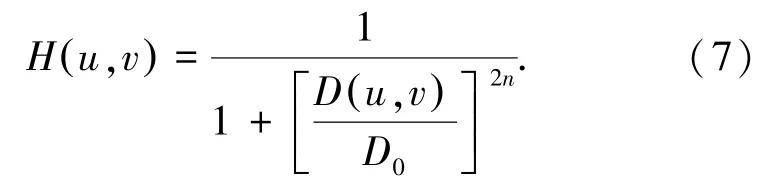
其中，D0为巴特沃斯低通滤波器的截止频率，n为巴特沃斯滤波器的阶数，n越大则滤波器的形状越陡峭。可以根据不同的滤波要求修改D0和n值，实现不同的图像增强效果［8］。

2.2 巴特沃斯高通滤波器

巴特沃斯高通滤波器传递函数H（u，v）可以表示为式（8）:

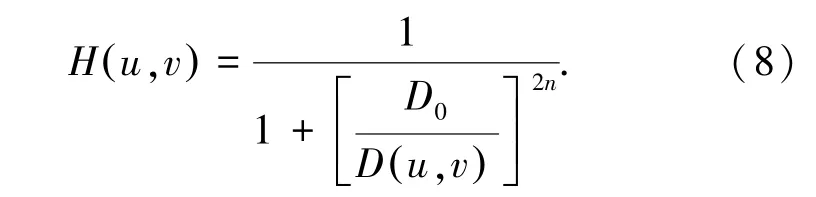
其中，D0为截止频率，参数n为阶数，用来控制滤波器的陡峭程度。

2.3 巴特沃斯带阻滤波器

巴特沃斯带阻滤波器的公式如式（9）:

其中，D0为需要截止的频率点与频率中心的距离；W为带阻滤波器的带宽；n为阶数。

3 巴特沃斯低通滤波器在图像增强算法分析

3.1 算法分析

为了实现巴特沃斯低通滤波器在图像增强的算法，本文在matlab中进行了2次不同的仿真实验。

（1）在原图上直接滤波，其算法实现步骤描述如下:

①通过imread（）函数读入图像；

②对图像进行傅里叶变换和平移，用fft2（）傅里叶函数变换图像到频域；

③设计阶数为6和截止频率不同的巴特沃斯低通滤波器，对图像实现滤波处理；

④用ifft2（）函数反变换回空域图像；

⑤用corr2（）函数计算滤波后图像和原图的相似度。

（2）对原图添加一定密度的椒盐噪声，再进行滤波，最后计算相似度。其算法实现过程如图1所示。

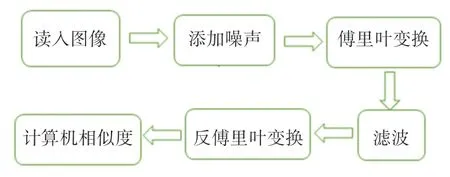
图1 算法流程图Fig.1 Algorithm flow chart

3.2 matlab算法实现的主要代码

在matlab中用巴特沃斯低通滤波器对添加椒盐噪声图进行图像增强仿真实验的主要代码如下:

A＝imread（＇coins.png＇）；%读入原图

I＝imnoise（A，＇salt＆pepper＇，0.02）；%添加密度为0.02的椒盐噪声

I＝im2double（I）；%转换数据类型

M＝2*size（I，1）；%设计滤波器的行数

N＝2*size（I，2）；%设计滤波器的列数

u＝-M／2:（M／2-1）；

v＝-N／2:（N／2-1）；

［U，V］＝meshgrid（u，v）；

D＝sqrt（U.＾2+V.＾2）；

D0＝50；%设置滤波器的截止频率为50

n＝6；%设置滤波器的阶数为6

H＝1.／（1+（D.／D0）.＾（2*n））；%设计巴特沃斯低通滤波器

J＝fftshift（fft2（I，size（H，1），size（H，2）））；%通过傅里叶函数转换到频域

K＝J.*H；%对加噪转换的频谱进行滤波处理

L＝ifft2（ifftshift（K））；%通过傅里叶反函数转换回空域

L＝L（1:size（I，1），1:size（I，2））；

r＝corr2（A，L）%计算机滤波后图与原图的相似的系数

figure；%显示各种图片

subplot（231）；imshow（A）；title（＇（a）原图＇）；

subplot（232）；imshow（I）；title（＇（b）加入 椒盐噪声图＇）；

subplot（235）；imshow（L）；title（＇（c）截止50频率＇）；

如果直接对原图进行滤波实验，只要将添加噪声的代码行删除即可，并且可以通过修改截止频率和滤波器阶数的数值来验证图像增强效果。

4 实验结果分析

4.1 实验结果

本文为了验证巴特沃斯低通滤波器对图像增强的效果，分别在matlab中进行2次仿真实验。

实验一设计阶数为6，截止频率分别为30、50、100、200的低通滤波器，对“coins.png”原图进行图像增强实验。

实验二对“coins.png”原图添加密度为0.02的椒盐噪声，设计阶数为6，截止频率分别为50、100、200的低通滤波器，对加噪图进行图像增强实验。

实验得到的相似度系数分别见表1、表2，图像增强实验后的对比结果如图2、图3所示。

图2 原图图像增强实验对比图Fig.2 Contrast diagram of original image enhancement experiment

图3 添加椒盐噪声后图像增强对比图Fig.3 Image contrast enhancement after adding salt and pepper noise

表1 原图图像增强相似度系数表Tab.1 Similarity coefficient table of original image enhancement

表2 添加椒盐噪声图像增强相似度系数表Tab.2 Similarity coefficient table of image enhancement with salt and pepper noise

4.2 结果分析

4.2.1 实验一结果分析

根据表1相似度系数客观评价图像质量发现:截止频率越低，数值越小，相似度也越低。对于图2（a），从主观评价分析发现，截止频率越低，图像越模糊。由此得出:巴特沃斯低通滤波器，在相同阶数的前提下，截止频率越高，拦截的高频信息越少，边缘平滑越少，图像边缘能保留的信息越多，图像与原图的相似度越高。

4.2.2 实验二结果分析

根据表2可知，截止频率不同，相似度系数也不同。当增加到一定的峰值后，截止频率继续增大，相似度反而会减少。由图3可见，图3（c）中椒盐噪声基本被滤掉，但图像与原图相比，图像较模糊；图3（d）中观察到，椒盐噪声也基本被滤掉，但是仔细观察还有一些淡淡的小点，即是没有滤掉的椒盐噪声，图像清晰度相对较高；尽管图3（e）图像清晰度是这三幅图中最高的，但是椒盐噪声还可明显看到，图像增强效果不是特别好。由此得出:巴特沃斯低通滤波器在阶数相同的情况下，图像的清晰度并没有随截止频率不断增加而增强，而是当截止频率到达一定的峰值后，截止频率增加，清晰度反而降低。这是因为椒盐噪声主要集中在图像的高频部分，当截止频率增加，拦截的高频信息越少，滤去噪声效果就降低，噪声能保留的信息越多，图像增强效果就会降低。因此，为了达到最好的图像增强效果，需要经过不断的实验，找到合适的截止频率，在保证图像质量的同时还能有效滤去椒盐噪声。

5 结束语

通过设计不同阶数和截止频率的巴特沃斯低通滤波器，能使图像中的低频部分信息顺利通过，高频信息有效拦截，达到平滑图像的目的，实现图像增强。在图像传递过程中，图像通常都会产生各种噪声，而噪声大部分都集中在图像的高频部分。本文通过实验证明:只要选择合适阶数和截止频率的巴特沃斯低通滤波器，就能有效去除图像中的椒盐噪声，改善图像质量，实现图像增强效果。但是，拦截噪声的同时也会把图像的一些高频边缘信息滤掉，引起图像边缘模糊。当截止的频率升高，噪声滤去的效果也会降低，因此选择合适阶段和截止频率是巴特沃斯低通滤波器设计的关键。