高中数学教学中的学情分析与难点设计研究

刘仁贵

摘 要：高中数学作为一门基础学科，应当加强课堂教学设计，构建高效课堂。想要实现课堂教学的有效性，需要做好学生学情分析，优化教学难点设计，帮助学生夯实基础知识，突破课堂教学难点。通过对学生学情和难点进行分析，结合学生学习水平和能力，考虑数学学科特点，做好教学难点设计，保证课堂学习效果。本文通过对学情和难点进行研究，在学生学情下，提出几点有效的难点设计策略。

关键词：高中数学;学情分析;难点设计;有效策略

顾名思义，学情是指学生学习过程中知识的掌握、技能的形成、智能的发展等一系列客观过程，教师对于学情的充分了解，是其从整体上把握教学的关键。而在数学学科中，将学情分析与教学难点形成科学的衔接，能够展开科学的难点教学设计，从更科学、更有效的角度指导学生，提升难点教学效果。因此，为有效的开展学情分析工作，避免数学难点教学的盲从性，形成真正以学生发展需要为基础的教学设计，文章以高中数学教学为研究对象，展开学情分析以及难点教学设计的研究，以期真正实现学生的主体地位，确保学生能力发展条件充足。

一、高中数学学情分析与难点设计

（一）学情分析

学情分析在教育领域又被称作学生分析、教学对象分析，其具有极为明确的指向性，以学生为中心展开的情况分析，其中情况包括两部分内容，即学生学习情况与学生身心发展情况，因此，为确保全面概括分析内容，命名之学情分析。学情分析在最初提出时，有四项目的：（1）将学情作为研究资源，反馈高中生数学学习的一般规律;（2）改进教学，以学情了解学生学习需要、能力薄弱点，对教学作出针对性优化与改进;（3）科学指导学生个性发展，学情分析对学生身心情况做出细致了解，是教师掌握学生个性、指导学生发展的依据;（4）教学反思依据，基于学情分析结果思考教学中的不足与缺陷[1]。

学情分析作为一项长期性任务，其不仅要关注、观察学生的日常表现，了解学生个性、学习风格，基于客观的理论与直接证据从客观层面展开全面分析。从而决定学情分析的主要内容有学习基础情况、学习动机与学习态度、学习方法与学习习惯。同时，学情分析是由教师开展的一项活动，基于教师对理论认识及与实践的结合，用心观察每位学生、客观分析每位学生，常见的学情分析方法有观察法、材料分析法、问卷调查法、访谈法。

在新课改背景下，基于“以人为本”的核心教育理念，要求高中数学教学必须面对每一名学生，关注每名学生的发展需要，为学生创造条件与空间，而不是基于素质教育目标挑选适合被教育的学生，因此，要求学情分析当中教师始终树立“以学定教”理念，基于对学生情况的全面了解与分析，不断提升教学设计的预见性与针对性，确保教学设计的每项内容基于客观的依据、学生的需求建立，为学生能力发展奠定坚实基础。由此总结来看，学情分析的现实意义体现在以下方面：（1）教学内容分析的必要前提;（2）优化教学目标的科学依据;（3）教学活动与教学方法选择的基础导向。

（二）难点设计

教学难点是指不易被学生理解的知识或不易被学生掌握的技能。在高中数学教学中，难点不等同于教学重点，但难点往往伴随着重点出现，所以，要求教师根据学生情况以及能力水平确定教学难点，并考虑个体差异下形成的不同的教学难点;且面对教学难点，需要教师采取有效的办法突破学生的思想束缚，打破思维常规，实现准确理解。基于此，明确了教学难点与学情分析之间存在着必然联系，基于学情分析确定教学难点，并基于学情分析选择合适的突破难点的方法，考验教师对教学整体的把控以及教学能力水平。

二、立足学情分析的高中数学教学难点设计策略

（一）分析高中生能力水平与思维特点

高中阶段，随着学生年龄的增长，智力发育也逐渐走向成熟，逐步趋近于成人水平，其逻辑思维以及认知也正经历着转型，由经验型转变为理论型，但受生理发育以及环境等多方面影响，高中阶段学生的个性存在特殊情况，过分地想要展现自我想法、表达自我对社会的认识，因而，在教学中，对于问题的思考以及探究性学习活动中常常能够提出自己的想法与间接，其并非为了得到他人的赞同而表达，很多学生单纯的渴望表达自己[2]。

（二）分析高中数学教学特点

与中小学数学相比，高中阶段数学学习难度有了大幅度提升，主要表现在语言的抽象性更强、思维方法逐渐向理性层面过度、知识体量加大、知识独立性提升，因此，教学中教学难点的存在更加普遍，解决高中数学学习难点将成为教学设计的重要内容，从而必须立足学生实际情况，确保难点教学有效性。

（三）高中数学教学难点设计实例——以几何教学难点為例

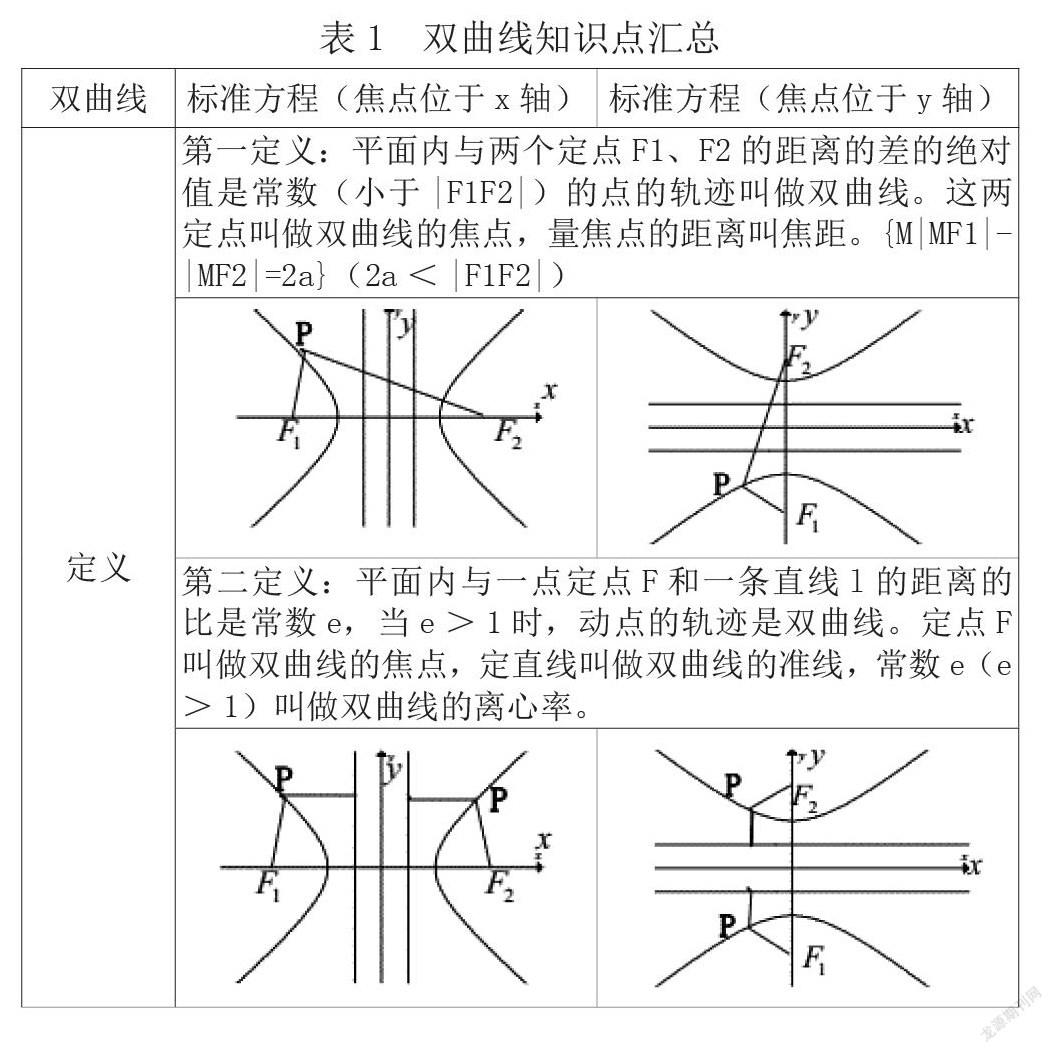
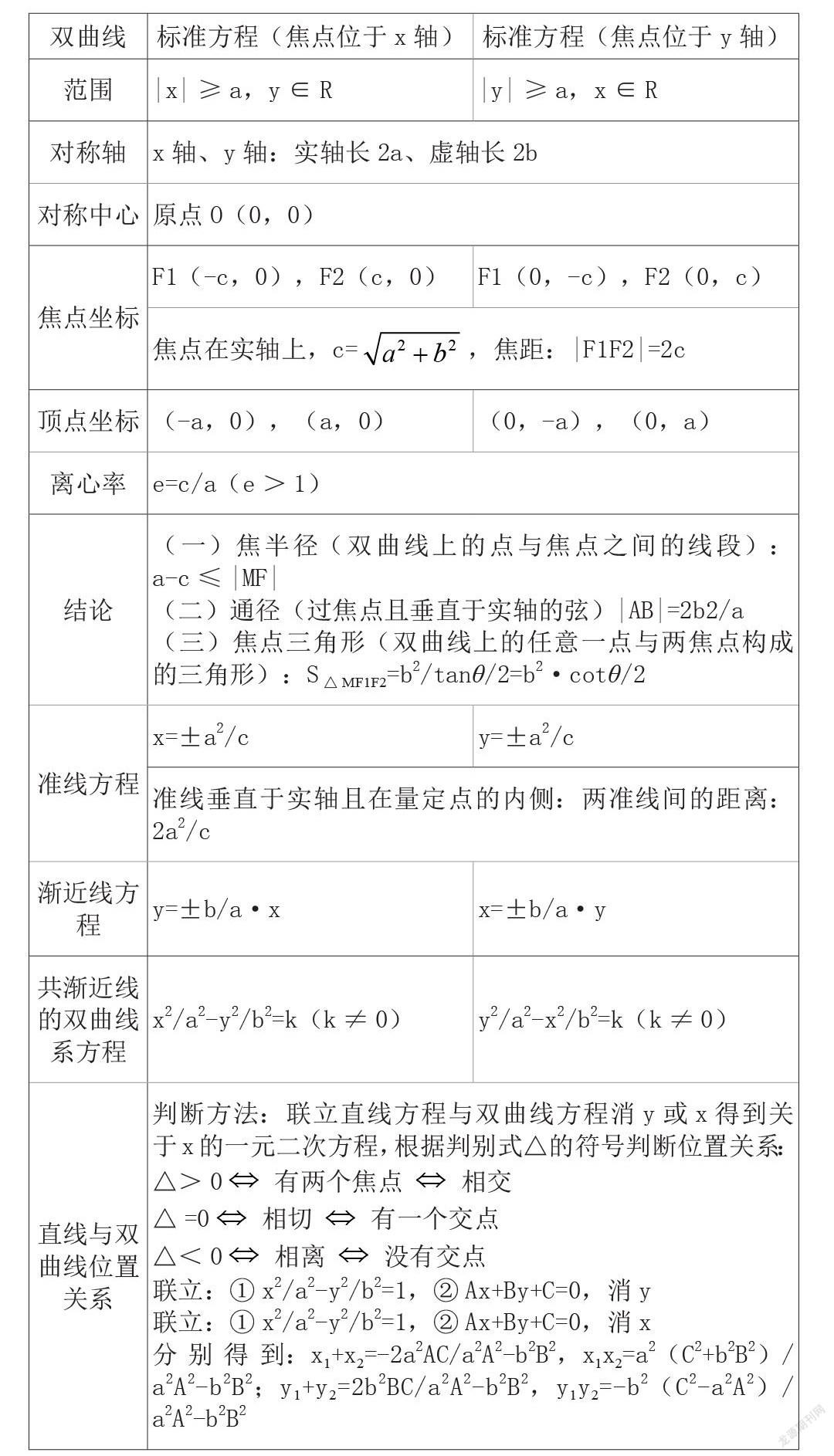
高中几何为高中数学教学内容的重要组成部分，虽然在小学、初中均对几何知识有所涉猎，但高中阶段几何知识概念愈发抽象、题型愈发综合，且考察常以大题形式出现，学生掌握不好，则导致考试中失分较多，几何教学为高中数学教学重难点在一线教师队伍已形成共识。高中的几何知识主要涉及直线、圆与方程、椭圆、双曲线、抛物线等，虽然学生在以往了解过，但难度与综合性均有所提升，且知识点密集、概念相似度高，学生容易混淆。因此，教学中常以比较法展开教学，帮助学生掌握几何概型的实质。

例：在双曲线教学过程中，形成系统的表格对比焦点在x、y轴上的标准方程，以及双曲线第一、第二定义，使学生准确区分两者不同，做出区别认知，避免知识点混淆。

学情分析下的高中数学难点教学是基于学生学习需要与能力发展需要实现“以学定教”的科学路径，高中数学教师应高度重视、科学分析，展开合理、有效的教学设计，以帮助学生突破难点。

参考文献

[1]江春、沈宏.基于高中数学核心素养的课堂教学——以三角函数的图像和性质教学设计为例[J].中学数学（上），2018（7）.

[2]张定强、裴阳.高中数学教育研究的热点与未来展望——基于2018年度人大复印报刊资料《高中数学教与学》转载论文的分析[J].中学数学（上），2019（4）.