荔枝差压预冷的数值模拟与实验研究

胡时发，张晨阳，王 达，张 哲，杨相政，徐双喜

（1.天津商业大学，天津 300134；2.中华全国供销合作总社济南果品研究院，山东济南 250204）

荔枝是6、7 月份主要盛产于我国广东、广西等地的名贵水果，深受人们喜爱，但由于产期处于高温高湿季节，其品质极易受损，需辅以保鲜措施来延长荔枝的保鲜期[1]。预冷作为果蔬冷链物流的最先一公里，对果蔬的保鲜期有着显著的延长作用，对于荔枝在市场上的流通有重要的意义[2]。

差压预冷是荔枝采后较适宜的预冷方式之一，在生产实际中，预冷压降对装置风机的选型以及能耗有重要的意义[3]。目前不少学者通过实验研究了差压预冷的降温特性，但对通风阻力特性的研究较少，尤其是涉及小果径果蔬的研究则更少。Vigneault 等[4]通过实验得到了风速在0.05～3.72 m/s 范围内包装箱里的25 种商品（球状果径最小为47 mm）Ramsin 方程的系数a 和b。吕恩利等[5-8]通过差压预冷实验对龙眼、荔枝、番茄的通风阻力特性做了相关研究，给出了包装箱开孔率的取值范围以及Ramsin 方程的拟合式等。黄健等[9-10]以黄瓜为研究对象，对圆柱形果蔬的流动阻力特性进行了实验研究，获得了空气流量与压降的关系。众多学者关于阻力特性的研究多以实验研究为主，耗费大量的人力物力，近年来随着计算流体力学的迅速发展，仿真精度较早期更高[11-13]，但应用性研究较少，本文采用fluent 仿真软件，以数值模拟结合实验验证的方式对荔枝差压预冷的通风阻力特性进行了研究。

1 材料与方法

1.1 材料与仪器

实验材料采用产自广东的‘妃子笑’荔枝，该品种果大、肉厚、色美、核小、味甜，品质风味优良。荔枝采摘后通过顺丰冷链从广州隔天运送至济南果品研究院保鲜贮藏实验室，并进行实验。

自制差压预冷装置一套，低温冷库一间。日本千野公司生产的MR5300 防水型温度传感器，精度为±1℃±1digit（-5～50 ℃范围内精度为±0.5 ℃±1digit），1 min记录一个数据。希玛AR866 手持式热敏式风速仪，风速测量范围为0.3～30 m/s；当速度小于10 m/s 时，测量误差为1%+1，风速超过10 m/s 时，测量误差为5%+1。testo512 型迷你压差测量仪，压差测量范围0～100 hPa，测量精度为±0.03 hPa（0～0.3 hPa）、±0.05 hPa（0.31～1 hPa）、±0.1 hPa+1.5%（1.01～100 hPa）；分辨率：当速度小于10 m/s 时为1%+1、风速超过10 m/s 为5%+1。差压预冷实验图见图1。

图1 差压预冷实验图Fig.1 Experimental diagram of forced-air precooling

1.2 物理模型

本文预冷模型采用截面为120 mm×120 mm 通道，主要由风机、PWM调速器、静压腔、水平通风管道组成。采用直径1 mm 的铁丝制成孔为10 mm×10 mm 的铁网作为荔枝的盛放容器，其外尺寸为120 mm×240 mm×120 mm（X×Y×Z）（如图1、2 所示）。

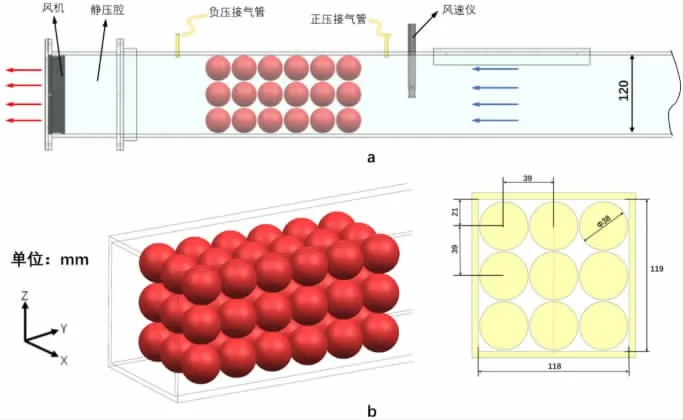
图2 实验与仿真模型结构Fig.2 Structure of experimental and simulation

1.3 实验方法

将新鲜的常温荔枝随机放入容器内，实验测得荔枝平均直径约为37.5mm，平均单果质量25g，总质量1 687 g。采用温度计实时监控并记录荔枝预冷过程的温度变化，布置果心温度测点共7 个位置如图3 所示，另外布置在进风口2 个；将荔枝放入预冷通道内，在容器的进风端布置风速传感器来监控实时风速；进风和出风两端布置压差传感器采集压差数据。装置风机采用PWM法调节风机转速，从而实现不同的送风速度。

图3 温度测点位置Fig.3 Location of temperature measurement point

1.4 数值模拟方法

1.4.1 数学模型

为方便数学模型的建立与计算，对预冷过程做了必要的假设：（1）忽略预冷包装箱外部条件对预冷效果的影响；（2）荔枝近似为球体且热物性参数不随温度的变化而变化；（3）空气的热物性参数为常数，为不可压缩流体；（4）忽略单体之间接触、辐射传热。SSTk-w湍流模型在处理流动分离和传热细节方面较为精确[14]，此次计算采用SSTk-w湍流模型进行求解。对于整个预冷模型利用平均雷诺数纳维-斯托克斯方程进行求解：连续性方程、动量方程、能量方程。对于流动和传热问题的求解都可以采用通用控制方程见公式（1）表示，公式涉及四项，为非稳态项，div（ρUφ）为对流项，div（Гφgradφ）为扩散项，Sφ 为源项。

式中，t-时间，s；ρ-流体密度，kg/m3；U-流体的速度矢量，m/s；φ-通用变量，可以代表u、v、w、T等求解变量；Гφ 为广义扩散系数；Sφ 为广义源项。

1.4.2 计算方法

计算方法采用压力速度耦合方法中的SIMPLE 算法，设置动量、能量、湍动能、扩散率的离散格式为二阶迎风格式，采用三维瞬态模拟进行计算。

1.4.3 初始条件与边界条件

边界条件：（1）荔枝与预冷通道内的空气接触面为流固耦合边界条件；（2）考虑通道的壁面的压降且外界对壁面没有传热影响，将通道壁面设置为无滑移绝热壁面；（3）进口边界设置为velocity-inlet，送风温度根据实验测得平均值设置为1 ℃，送风速度分别设为0.5、1.0、1.5、2.0、2.5 m/s；（4）出口边界设置为out-flow。

初始条件：荔枝与通道内空气的初始温度都设置为25 ℃，模型涉及到的物性参数如表1 所示。

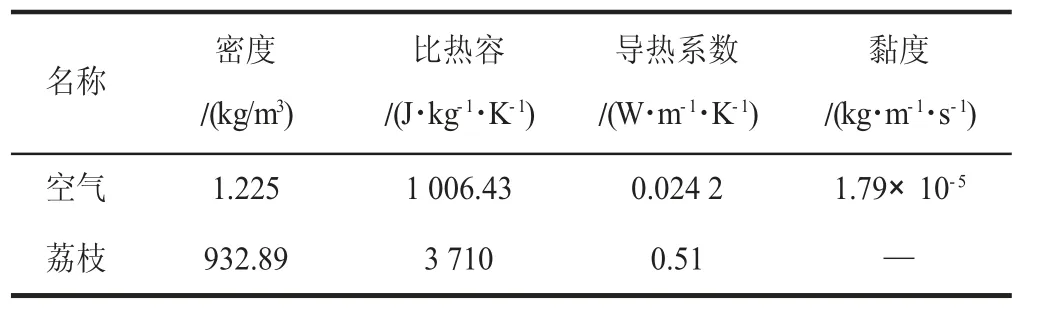
表1 模型材料的物性参数Table 1 Physical property parameters of model materials

1.4.4 网格划分与网格独立性验证

模型网格采用fluent meshing 划分多面体网格，其优点是适合复杂几何，数量较四面体、六面体都要少，且适用于处理回流问题，在计算精度和收敛性上也不弱于四面体和六面体网格。荔枝与荔枝及壁面实际上是相切的，为了保证网格质量和计算的收敛，相切的地方均留出一定的空隙[15]。

本文分别划分了数量为22、61、131、276 万的网格进行了独立性检验，采用差压预冷过程最为重要的两个参数（果品的平均温度及压降，30 min 时刻）作为判断依据，其结果如图4 所示。

图4 压差和温度随网格数的变化Fig.4 The pressure drop and temperature under different mesh numbers

从图4 可以看出，计算进行到30 min 时，网格数量在131 万后，压降的值已趋于平缓，而温度整体变动的幅度不大，所以认为网格数量在131 万的基础上继续细化网格对最后的仿真结果精度提升不大。最终模型网格数量确定为131 万，网格节点数433 万，并采用aspect ratio划分5 层边界层网格，如图5 所示。通过fluent 网格质量报告，整体网格的Orthogonal Quality 大于0.5，aspect ratio小于50。

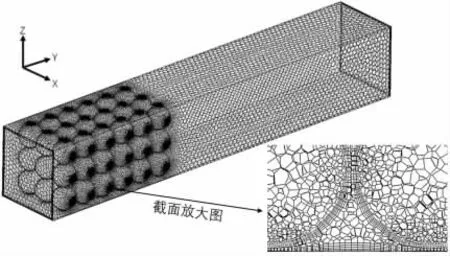
图5 模型网格Fig.5 Grid of model

2 结果与分析

2.1 降温过程

预冷速率作为差压预冷最重要的评价指标，是判断仿真结果是否精确的重要参数[11]。图6 显示了同一时刻、同一位置、不同风速下荔枝的温度云图，结果表明在图中所示风速范围内风速越大，预冷速度越快。

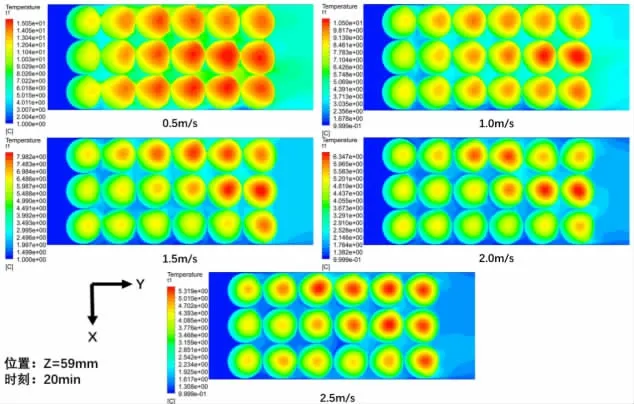
图6 不同风速下荔枝的温度云图Fig.6 Temperature nephogram of litchi at different airflow rate

图7 给出了不同风速下仿真和实验的预冷平均降温曲线，实验数据与仿真数据吻合较好，图8 给出了不同风速下实验与仿真数据的相对偏差。相对偏差值总体小于15%，仿真模拟的精度较高。从预冷降温曲线可以看出，预冷速率先快后慢，随着风速的提高，预冷速率加快，7/8预冷时间减小，当速度大于1.5 m/s 之后，预冷速率的变化幅度大幅降低，2 m/s 与2.5 m/s 的降温曲线基本重合，由此说明风速的提高对预冷速率没有显著影响，综合考虑该模型下1.5 m/s 为最合适的送风速度。

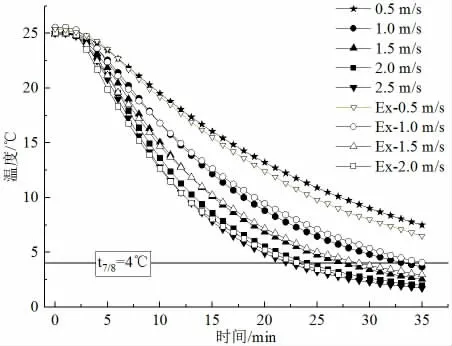
图7 不同风速下荔枝的平均降温曲线（仿真/实验Ex）Fig.7 Average cooling curve of litchi at different airflow rate

2.2 压降（△P）与风速（v）的关系

压降是差压预冷中不可忽略的一个重要指标，在实际生产中对风机的选型有着重要的意义，图9 给出了X=78.5 mm 平面上不同风速下的压力云图。从图中可以看到，随着预冷的进行，压力总体呈现随Y 轴逐渐降低的趋势，并且在荔枝之间的空隙处出现较大的梯度变化，杨洲等[13]研究表明压力的变化为锯齿状，与云图所示规律一致。

图9 不同风速下的压力云图Fig.9 Pressure nephogram at different airflow rate

图10 给出了压差随速度的变化曲线，从图中可以得到容器空载时的压降分别是0、0、0、1、2.25 Pa，可以忽略容器压降对实验的影响；压降的实验值相对于模拟值总体偏小，主要原因是在荔枝的填装过程中，荔枝的枝条没有修剪干净，且形状并不规则，增大了空隙，另外上层空隙也导致了压降的偏小。随着风速增大，差值偏离程度将越来越大。

图10 不同风速下压差的变化曲线Fig.10 The pressure drop at different airflow rate

图10 中实验值压差与速度的关系与Ramsin 方程[4,7-8]（△P=avb）的形式吻合，实验数据通过拟合可以得到该模型压差与速度的关系式为△P=18.49v1.97，R2=0.999。

2.3 压力P 与填装长度L 的关系

在实际生产中，风机的选型与果品沿送风方向填装的长度L（本文为Y 方向）有关，若风机压头过低，会出现“吹不透”的现象，导致预冷时间加长，且增加了不均匀度。图11 给出了不同速度下压力随Y 方向 [起点（78.5，0，59）、终点（78.5，300，59）]的变化，压力随Y 是逐渐降低的，呈锯齿状；这是由于模型果品沿Y 方向是分层排布，每通过一层就像通过收缩扩张喷管会出现明显的压降，整体呈阶梯式下降。

图12 给出了压力随长度L的变化图，下面仅讨论送风速度为1.5 m/s 的情况，这里L以出风口位置果品处为0 点，根据模拟数据进行线性拟合获得压力与长度L的关系式为P=0.211L-9.335，R2=0.955 4。

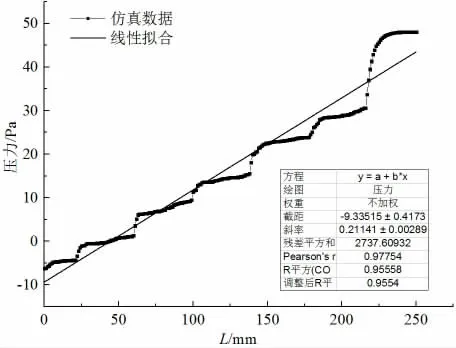
图12 压力随长度L 的变化图（v=1.5 m/s）Fig.12 Pressure varies with the length(v=1.5 m/s)

3 结论

本文采用fluent 仿真软件数值模拟和实验验证的方式研究了荔枝的差压预冷过程，通过分析降温过程中压降与风速关系以及压力与填装长度的关系得出：（1）该仿真模型的数值结果与实验数据吻合度较高，降温速率的相对偏差总体小于15%，由此验证了fluent 仿真模拟的准确性；并且发现该模型下1.5 m/s 为最适宜的送风速度；（2）根据Ramsin 基本方程，通过实验数据拟合得到该模型荔枝差压预冷过程中压降与速度的关系式；（3）在1.5m/s 的送风速度下，通过仿真数据获得了压力与填装长度的关系式，为风机的匹配选型提供参考依据。