基于地震反应谱分析的全直桩码头结构优化

汪 雨, 孙克俐

(天津大学 建筑工程学院,天津 300350)

高桩码头是一种较为常见的码头结构型式,全直桩码头是其中特殊的一种。为实现降低工程造价、改善结构受力状态、提高结构安全性的目标,国内外的研究学者和工程师已经针对高桩码头的优化设计开展了一些相关的研究工作。文献[1]以纵梁、横梁和桩基的数目作为设计变量,以最低造价为目标函数,采用离散复合形法对全直大管桩梁板式码头进行了整体布局优化设计;文献[2]采用Matlab软件和序列二次规划法,以基桩轴力标准差为目标函数,对某高桩墩式码头在最不利系缆工况下的桩基布置进行了优化;文献[3]基于有限单元理论、运用均匀化方法,对大跨度深水高桩码头在自重和堆货荷载作用下的纵梁结构形式进行了拓扑优化;文献[4]以靠船梁单位长度的造价为优化目标,对高桩码头靠船梁的截面尺寸、主筋及箍筋参数进行了局部优化;文献[5]以结构总体积为目标,对某内河底梁式全直桩码头进行了基于静力分析的构建尺寸优化。

目前针对高桩码头优化设计的研究大部分基于结构静力分析,而对动荷载作用下的结构优化设计研究则相对较少。全直桩码头作为一种特殊的高桩码头结构型式,其竖向荷载和水平荷载完全由直桩承受,受力情况比较复杂。而在码头承受的水平荷载中,地震作用是不可忽视的动荷载,一旦出现则量值很大、破坏性较强。因此,本文将振型分解反应谱法这一重要的抗震分析方法与码头结构设计紧密结合,在满足结构抗震设计要求的情况下,以降低造价为目标,通过调整排架间距、桩间距、桩基与上部结构尺寸,对全直桩码头进行整体布局优化。

1 数值模拟

1.1 工程背景

本文选取某全直钢管桩码头4榀排架×4排纵梁的结构段为研究对象进行地震反应谱分析和优化设计。码头面顶高程+5.0 m,码头前沿设计底高程-10.0 m,桩基底部标高为-31.0 m,结构重要性等级为Ⅱ级。该全直桩码头结构主要由面板、横梁、纵梁和桩基组成。其中:面板厚度为0.45 m;横梁高2.0 m,宽1.5 m;纵梁高1.6 m,宽1.2 m;纵梁间距5.5 m;横向排架间距6.5 m;每个横向排架布置4根基桩,基桩选用钢管桩,直径为1 200 mm,壁厚为17 mm。

1.2 材料参数

考虑到振型分解反应谱法中只有线性行为是有效的,码头中钢筋混凝土结构和钢管桩均采用线弹性本构模型,各类材料属性见表1所列。

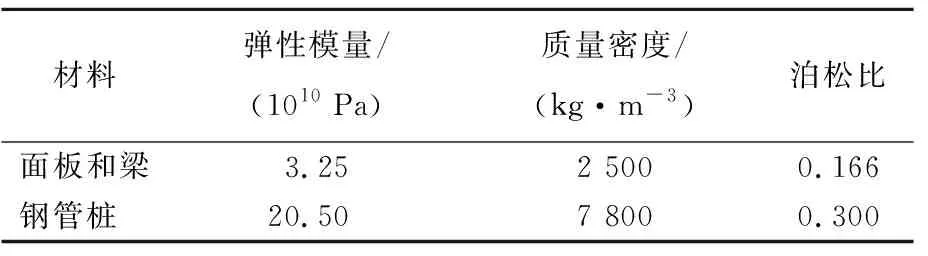
表1 结构材料参数

1.3 有限元模型建立

采用ANSYS参数化设计语言APDL建立的全直桩码头结构段空间有限元模型如图1所示。模型整体坐标为笛卡尔坐标系,x轴平行于码头前沿线,y轴垂直于码头面向上为正,z轴垂直于码头前沿线由陆侧指向水侧。模型中采用壳单元SHELL43模拟码头面板,采用梁单元BEAM188模拟纵横梁和钢管桩,通过定义截面偏移模拟梁板间的实际相对位置;采用质量单元MASS21模拟码头面上的堆载附加质量;采用桩轴向的弹簧单元COMBIN14模拟土对桩的垂直约束作用。码头结构各构件之间通过共节点实现整体的刚性连接;桩端采用弹性嵌固点法考虑,受弯嵌固点深度采用m法计算,取为6.0 m。

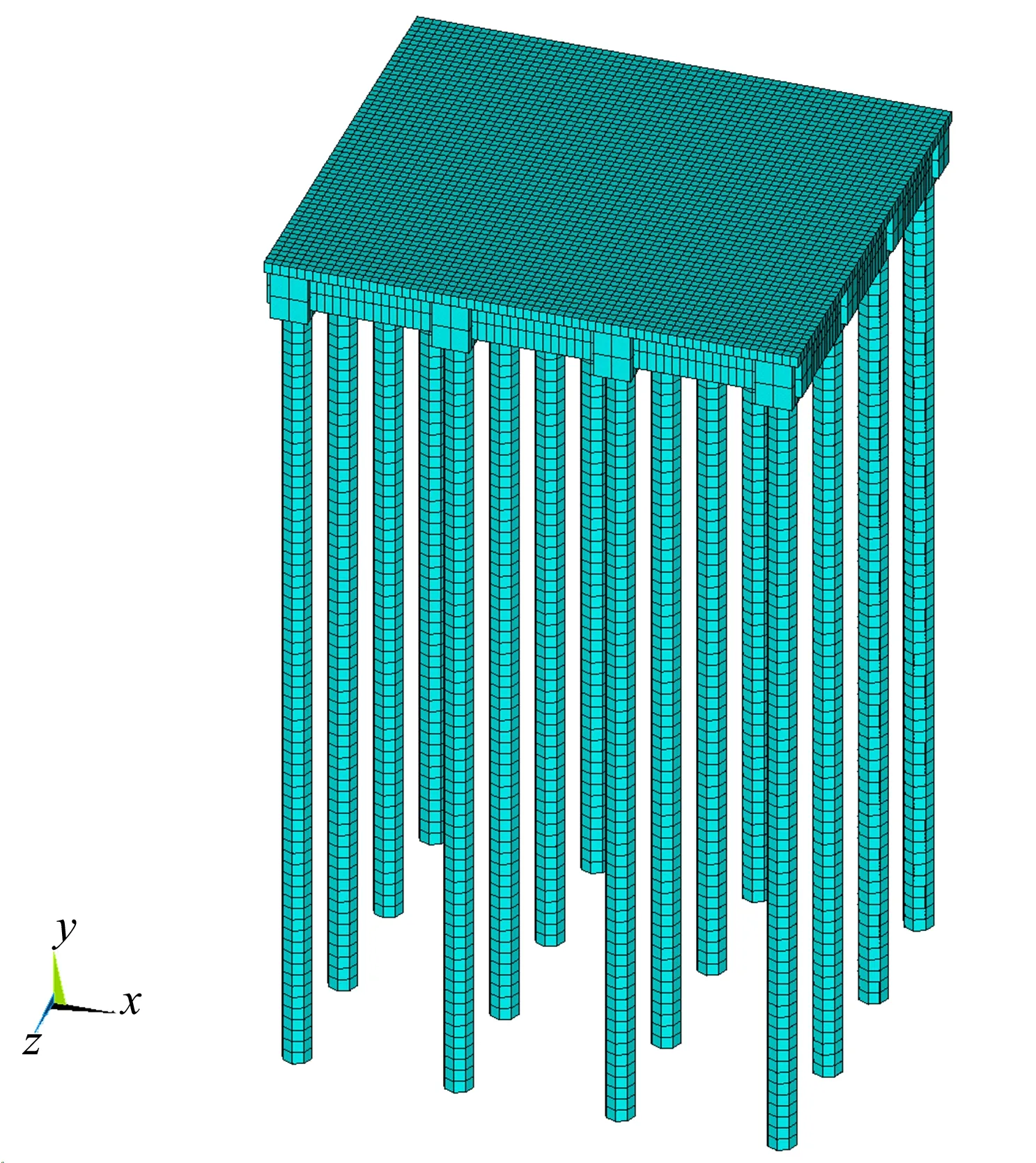
图1 全直桩码头有限元模型

1.4 地震反应谱的选取

本工程所在区域地震设防烈度为7度,场地复杂程度等级为Ⅱ级。结构阻尼比为0.05,水平向地震系数为0.1,采用JTS 146—2012《水运工程抗震设计规范》[6]中的β谱曲线进行水平地震响应分析,反应谱特征周期为0.35 s。

2 结构地震响应分析

2.1 自振频率和周期

采用分块Lanczos法对模型进行模态分析,提取前5阶模态的固有频率、周期及累计质量参与系数,见表2所列。

采用振型分解反应谱法进行结构抗震设计时,参与组合的振型有效质量之和需大于等于结构总质量的90%。

由表2可知,本模型进行反应谱分析时提取前3阶振型即可满足上述要求。

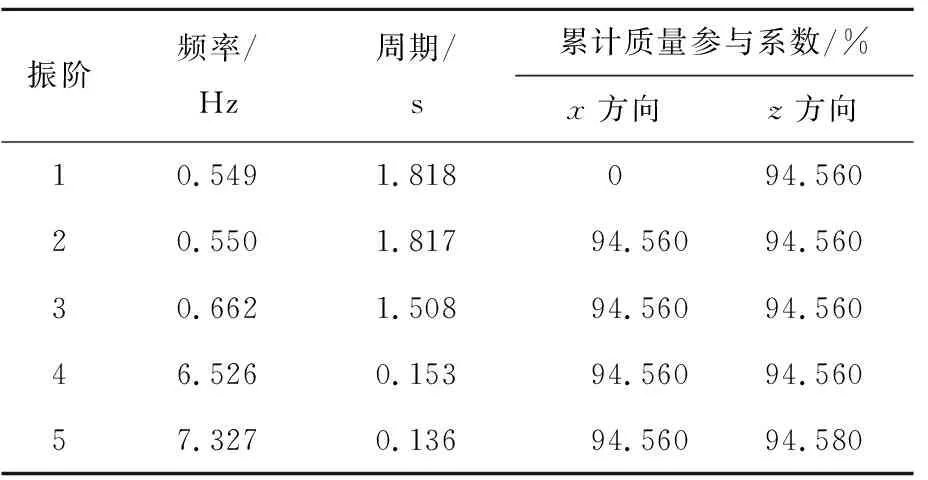
表2 结构自振频率及累计质量参与系数

2.2 结构内力和变形

本文利用大型通用有限元软件ANSYS计算水平地震作用下的结构响应。采用单点加速度反应谱,结合振型特征,分别从码头纵、横2个方向对全直桩码头结构段进行水平地震动激励,并按SRSS法进行效应组合,得到结构整体位移、应力及桩内力响应的最大值，见表3所列。

由表3可知,当前结构在其抗震设防烈度下各构件内力值相对较小,整体位移值也偏于保守,材料性能尚未得到充分的发挥。因此,在现有模型的基础上对结构进行优化设计,使其在满足抗震设计要求的基础上合理降低工程造价,是非常有必要的。

表3 初始结构地震响应最大值

3 抗震优化设计数学模型

3.1 目标函数

本文对全直桩码头进行结构优化的目的是在结构响应满足抗震设计要求的情况下,尽可能减少材料消耗、降低工程造价。

考虑到码头设计一般是先依据地形条件和使用要求确定平面尺寸,再对结构进行具体的设计,因此,取单位面积码头所需的材料体积为目标函数进行优化。

具体表达式如下:

(1)

其中,W为单位面积码头所需材料的体积,单位为m3;i为优化对象所包含的结构构件数量;Vi为各构件的体积,单位为m3;A数值取该工程段码头面积,单位为1。

3.2 设计变量

本文的研究目标是对全直桩梁板式码头进行整体布局优化,包括梁格和桩基布置方式及各构件尺寸优化。

因此初步选择面板厚度、横向排架间距、纵梁间距、横纵梁宽度、横纵梁高度、钢管桩半径、钢管桩厚度9个变量作为优化设计变量。

全直桩码头结构优化的设计变量及其取值范围见表4所列。

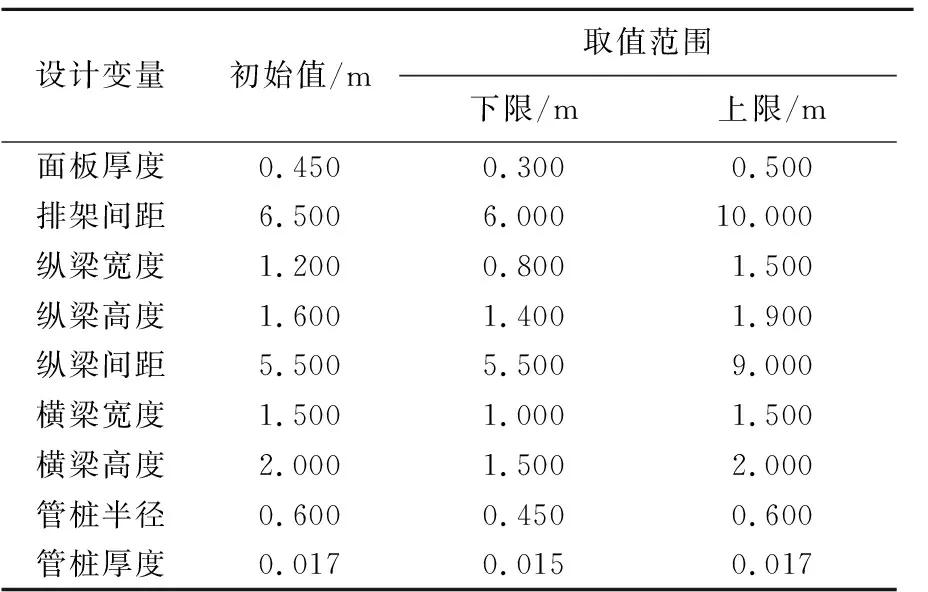
表4 结构优化设计变量及其取值范围

3.3 约束条件

考虑到结构各构件材料均已确定,因此主要考虑性能约束条件,即对结构在设计地震荷载下的变形和应力加以约束。

(1) 变形约束。表达式为：

|Umax|<[U]

(2)

其中:|Umax|为结构实际最大变形的绝对值;[U]为结构许用变形。

变形约束即结构在纵向、横向水平地震作用下的最大变形均要小于许用变形。由于本文主要是研究全直桩码头在水平地震作用下的结构优化问题,结构变形主要考虑水平方向最大位移值。现行相关规范并未对地震作用下的码头结构变形限值作出明确规定。因此,本文根据计算中出现的问题反复调整模型,最终确定结构变形上限值为35 mm。

(2) 应力约束。表达式为：

σmax<[σ]

(3)

其中:σmax为结构实际最大应力的绝对值;[σ]为结构许用应力。

应力约束即结构在在纵向、横向水平地震作用下的的最大应力值均要小于许用应力。建立模型时上部结构未考虑配筋,其许用应力难以确定。为简化计算,上部结构的许用应力值取C40混凝土的设计受压强度值19.1 MPa;桩基许用应力值取为70 MPa。

4 灵敏度分析

采用ANSYS优化模块求解抗震优化设计数学模型时,设计变量的数目越多,结构反应谱分析的次数也就越多,计算工作量随之增长,进而影响优化效率和优化收敛效果[7]。

因此,本文采用ANSYS的概率设计模块对目标函数(单位面积码头所需材料体积)进行灵敏度分析。首先假定抗震优化设计数学模型中各设计变量在其取值范围内服从均匀分布;然后采用拉丁超立方抽样法选取2 000个样本点;进而统计分析出设计变量的不确定性对于目标函数的影响行为及特性。

目标函数对各设计变量的灵敏度排序结果及灵敏度具体数值见表5所列。

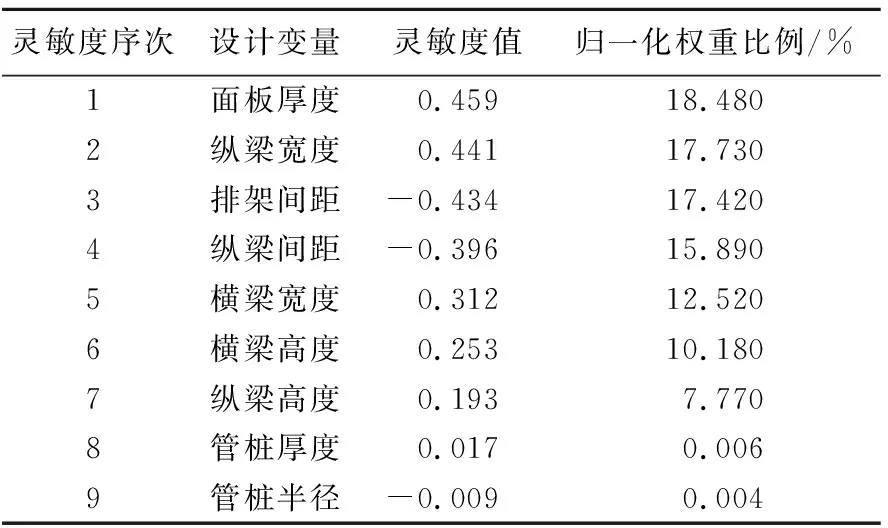
表5 目标函数对设计变量的灵敏度分析结果

表5中:灵敏度数值为正，表示该设计变量与目标函数正相关,为负则表示两者负相关,灵敏度绝对值越大代表该设计变量的取值变化对目标函数的影响程度越大[8];归一化权重比例表示的是该设计变量在所有设计变量中对目标函数的影响权重。

由表5可知,增大排架和纵梁的间距可有效减小目标函数的值,上部结构(面板和纵横梁)的尺寸参数对目标函数的影响较大,而桩基尺寸参数对目标函数的影响则相对小得多,因此,后续优化中不再对桩基半径和厚度进行优化。

5 优化数学模型计算结果

采用ANSYS优化模块中的零阶算法对精简设计变量后的抗震优化设计数学模型进行求解,经过14次迭代计算得到优化后结构与原结构的对比数据,见表6所列。

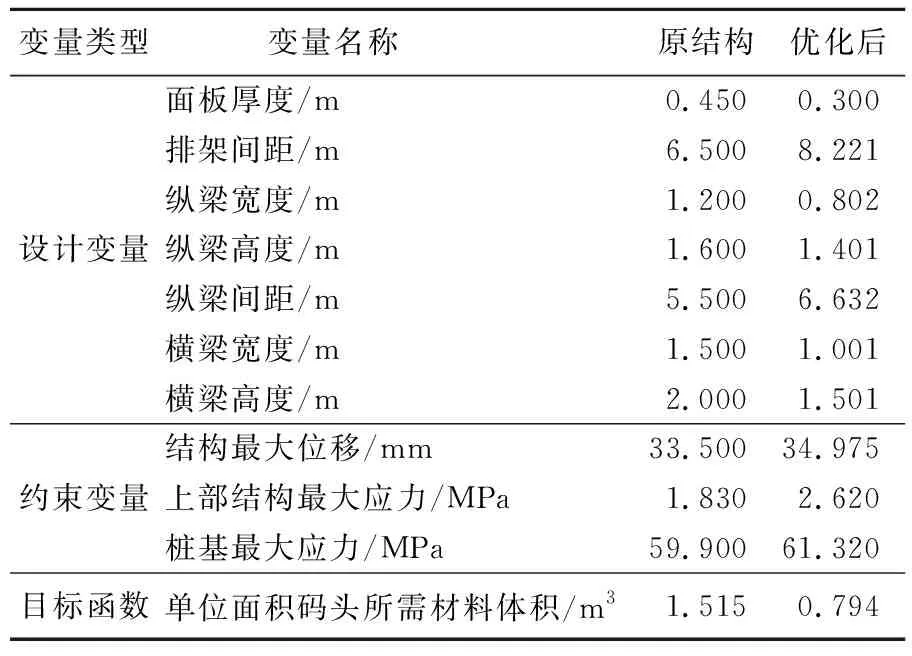
表6 优化后结构与原结构的对比

根据表6中数据可知,优化后结构面板厚度取为0.3 m,横向排架间距取为8.2 m,纵梁间距取为6.6 m,纵梁宽度、高度分别取为0.8、1.4 m,横梁宽度、高度分别取为1.0、1.5 m。与原结构相比,优化后的结构排架间距、纵梁间距和管桩半径有所增大,其他变量则均有所减小。优化后的结构在地震响应满足约束条件的情况下,单位面积码头所需材料体积由1.514 8 m3减少至0.793 6 m3,优化率达到了47.6%。

优化后的全直桩码头结构在纵、横2个方向水平地震动激励作用下的整体位移、应力及桩基内力最大值见表7所列。

表7 优化后结构地震响应最大值

对比表3和表7中数据可知:与初始结构相比,优化后结构在单位面积用料显著减少的情况下位移和应力响应的最大值仅有微小幅度的上涨,但仍处于约束条件的范围之内;优化后结构在纵向、横向地震作用下的响应最大值基本相近,可见纵向刚度与横向刚度大致相等,整体抗震性能良好。

6 基于优化模型的结构型式优化

6.1 底梁式结构模型建立

在抗震优化设计数学模型计算所得结构的基础上,从结构型式的角度对全直桩码头进行进一步优化:保持单位面积码头所需材料体积基本不变,将原有顶层横、纵梁的截面尺寸适当缩小,同时在顶梁下方8 m处增设底层横、纵梁。

梁截面尺寸见表8所列,增设底梁后的结构模型如图2所示。

表8 2种结构型式的构件尺寸

图2 底梁式全直桩码头有限元模型

对无底梁结构与底梁式结构模型分别施加横向水平地震设计反应谱,经过计算得到2种结构的最大侧向位移分别为35.0、23.2 mm,最大应力分别为60.7、48.8 MPa。这一结果表明:在材料用量基本不变的情况下设置底梁可以有效限制结构在水平地震作用下的侧向变形,减小结构应力,但其具体作用还需进一步分析。

6.2 底梁作用影响分析

为进一步探讨设置底梁对结构抗震性能的影响,保持构件尺寸参数不变,通过改变底梁与顶梁之间的间距变化底梁位置,建立5组底梁式结构模型和1组无底梁结构模型,分别进行横向地震作用下的反应谱分析,从结构最大位移、桩基内力及横梁内力3个方面对结构的地震响应进行对比分析。

6.2.1 底梁对码头结构最大位移的影响

1组无底梁结构和5组底梁式结构的最大位移响应见表9所列。在相同烈度的横向地震荷载作用下,底梁式结构最大位移响应均小于无底梁结构,减小幅度达到20%～36%;且随着底梁与顶梁间距的增大,位移减小幅度逐步增大,并在间距为10 m时幅度达到最大;此后梁系间距继续增大而位移减小幅度却有所降低。

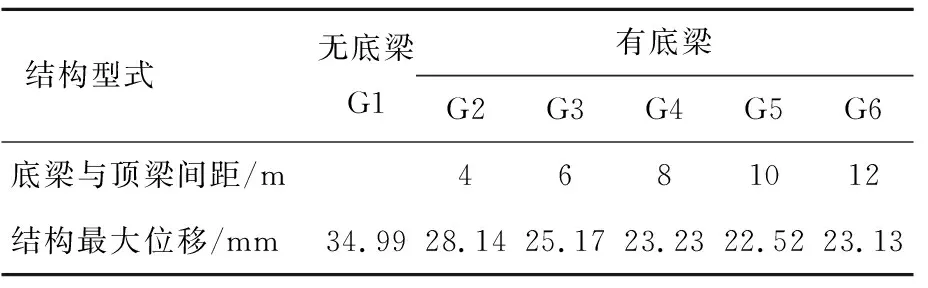
表9 结构的最大位移响应

6.2.2 底梁对码头桩基内力的影响

选取最左侧排架近海侧第1根桩基为研究对象,对其进行受力分析,得到各组结构模型中该桩的剪力及弯矩的对比结果，如图3、图4所示。

由图3可知：随着底梁与顶梁间距的增大,桩顶部剪力值逐渐增大,泥面下桩剪力值则逐渐减小且均小于无底梁结构;当梁系间距小于8 m时桩顶剪力小于无底梁结构,当梁系间距大于8 m时桩顶剪力大于无底梁结构。

图3 桩基剪力的对比

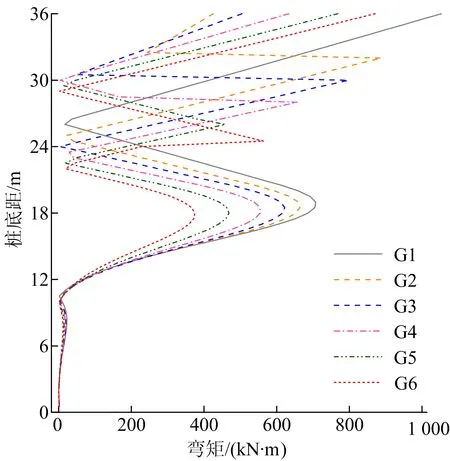
图4 桩基弯矩的对比

此外,5组底梁式模型(G2～G6)的桩身剪力均在桩基与横梁连接处发生局部突变,相比于桩顶部剪力有所增长,该涨幅随着底梁与顶梁间距的增大而逐渐减小。

由图4可知:在设置了底梁的5组模型(G2～G6)中,桩身弯矩峰值均出现在各自的桩顶处、底梁与桩基连接处及泥面附近;随着底梁与顶梁间距的增大,桩顶处弯矩峰值逐渐增大,底梁与桩基连接处及泥面附近的弯矩峰值则逐渐减小。

分析表明:① 设置底梁后,水平荷载由底梁和顶梁共同传递,使得较大的水平集中力转变成了较小的分散力作用在基桩上,使基桩受力更为均匀,桩顶弯矩减小;② 底梁位置越高,其分担水平力的贡献越大,但容易造成桩基与底梁连接处的剪切变形破坏。

6.2.3 底梁对码头横梁内力的影响

由桩基内力对比结果可以初步判断底横梁主要起到传递轴力的作用,因此,选取最左侧横向排架的顶横梁和底横梁为研究对象,对其进行受力分析,分别得到各组模型中顶、底横梁的轴力对比结果如图5和图6所示。

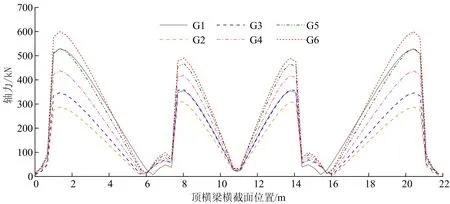
图5 顶横梁轴力的对比

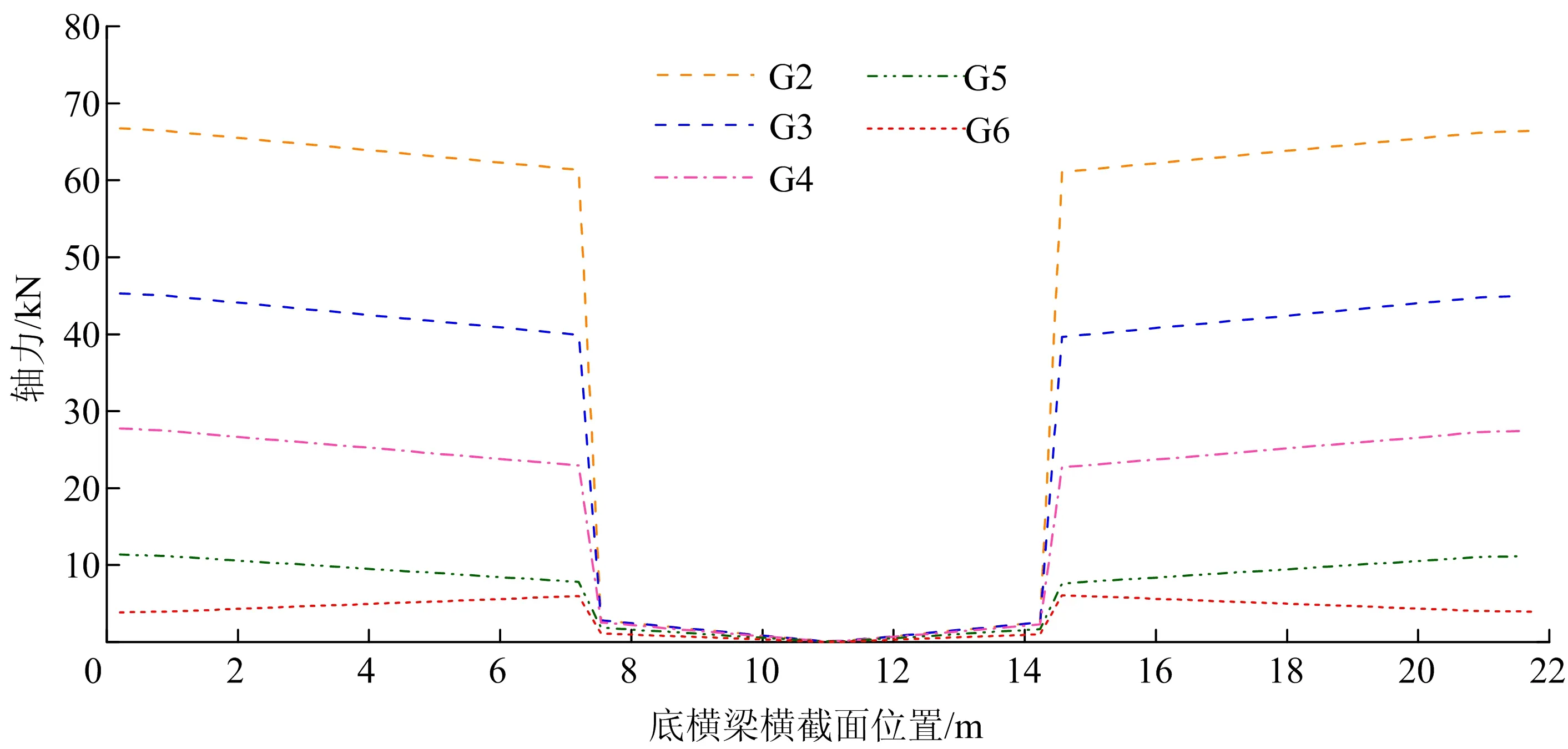
图6 底横梁轴力的对比

由顶、底横梁轴力对比结果可知：随着底梁与顶梁间距的增大,顶横梁各处轴力值逐渐增大,底横梁两侧的轴力值逐渐减小，中部轴力基本不变且数值较小;当梁系间距小于8 m时,底横梁两侧轴力值远高于中部轴力值;当梁系间距大于10 m时,底横梁整体轴力值偏小且顶横梁轴力值已超过无底梁结构。

分析表明:① 底梁设置在顶梁下方10 m时,结构位移响应峰值达到最小,且结构整体受力较为均匀且合理;② 底梁位置较高时,其轴力传递作用更显著,且两侧分担水平力的贡献相对更大,但可能会造成底梁受力不均匀;而底梁位置过低时,底梁对水平力的分散传递作用则不太显著。

7 结 论

(1) 本文所采用的全直桩码头结构优化设计方法将反应谱法这一常用的码头抗震设计方法与结构优化数学模型相结合,利用ANSYS完成参数化有限元分析模型的建立及优化数学模型的求解,并辅之以灵敏度分析技术。经过该方法优化后的结构地震响应均在设计要求的约束范围之内,且整体优化效果较好,说明该优化方法可靠且有效。

(2) 在合理范围内缩减顶梁尺寸、增设底梁的全直桩码头结构不仅可以满足经济性要求,而且整体刚度增大，抗震性能表现更优。

(3) 对于底梁式全直桩码头结构,在一定范围内降低底梁的位置可以有效地减小结构在水平地震作用下产生的侧向变形;但底梁位置过低时,其对于结构抗震性能的提升作用则非常有限,且可能会造成构件内力值的增大。