贪婪初始种群的遗传算法求解柔性作业车间调度

屈新怀, 王 娇, 丁必荣, 孟冠军

(合肥工业大学 机械工程学院,安徽 合肥 230009)

柔性作业车间调度问题突破了设备资源唯一性的限制,每道工序可由不同的机器加工,并且在不同机器所需的加工时间不同,其主要考虑机器选择和工序排序这2个问题,是作业车间调度的扩展,更加符合生产实际[1]。柔性作业车间调度问题是制造业信息化的重要内容,也一直是国内外学者研究的热点,是典型的NP难问题。

目前,研究柔性作业车间调度问题常用的算法是智能优化算法,其中,遗传算法因其全局搜索能力强、鲁棒性好被广泛地应用于柔性作业车间调度问题上,但是遗传算法也存在收敛速度慢、易早熟等不足以及种群多样性不足的缺陷[2]。为了提高算法性能,国内外学者在求解柔性作业车间调度问题时,从各个方面对遗传算法进行改进。文献[3]针对柔性作业车间调度问题特点提出主动调度的插入式解码机制;文献[4]针对柔性作业车间调度问题采用层次多空间竞争遗传算法进行有效的层次优化;文献[5]提出自适应交叉和变异概率;文献[6]将遗传算法与其他智能算法相结合求解柔性作业车间调度问题。还有许多学者对初始化方法进行了改进。文献[7]基于短用时策略的指派方法生成初始种群;文献[8]提出一种全局搜索、局部搜索和随机产生相结合的初始化方法;文献[9]采用同时考虑处理时间和工作量的启发式方法与随机产生相结合的策略生成初始种群;文献[10]提出基于全程检索规则编码的初始种群生成策略。以上初始化方法分别为每个工件选择机器,却没有考虑不同工件工序之间的相互影响。

本文结合柔性作业车间调度问题的特点,提出贪婪初始化方法,随机为工序排序,然后采用贪婪算法按工序的排序为每个工序选择当前加工时间最短的机器,从而生成较优的初始种群,为了保证解的多样性设计了贪婪初始化与随机生成相结合的初始化方法;在进行选择操作时先筛选出机器染色体相同的种群,并通过初始化方法生成新的种群进行替换,使得算法在求解过程中能有效地跳出局部最优。

1 问题描述

柔性作业车间调度问题可以描述为n×m问题:n表示车间内有n个待加工工件;m表示车间内有m台可选择加工机器;n×m表示n个工件在m台机器上加工的柔性作业车间调度问题;J={J1,J2,…,Jn}表示工件集;M={M1,M2,…,mn}表示机器集;Oi={Oi1,Oi2,…,Oij}表示工件Ji的工序集;Mij⊆{M1,M2,…,Mm}为每道工序Oij的可选择加工机器集,每道工序在不同机器上都有相应的加工时间。柔性作业车间调度为工序安排最佳的加工顺序和选择最佳的加工机器,以达到优化给定性能指标的目标,其中3×3问题见表1所列。

表1 3×3问题

本文柔性作业车间调度问题以最大完工时间最小为优化目标,目标函数可表示为:

minCmax=min(maxCi), 1≤i≤n

(1)

其中:Cmax为工件最大完工时间;Ci为工件Ji的完工时间。

对于柔性作业车间调度问题,需满足的约束条件[11]如下:

(1) 在零时刻,所有设备都是空闲的,所有工件都可以被加工。

(2) 不同工件之间具有相同的优先级,同工件的工序严格按照加工顺序加工,每道工序必须在其前一道工序完成后才能进行。

(3) 每道工序只能从可加工机器集中选择一台进行加工。

(4) 每道工序一旦开始,加工过程不中断。

(5) 同一时刻的各台机器最多只能加工一道工序。

2 算法设计

2.1 编码与解码

柔性作业车间调度问题要同时考虑工序排序和机器选择2个方面,因此采用分段编码方式:前段为工序排序染色体编码,用来确定工序加工顺序,数值i表示工件号,而数值出现的次数j表示该工件的第j道工序,对应的工序为Oij;后段为机器选择染色体编码,机器编码按顺序为工件J1,J2,…,Jn的工序选择的加工机器,用数值s表示选择该工序可加工机器集合中的第s台机器,如图1所示。

图1 染色体编码

2.2 贪婪初始化

初始种群的质量对遗传算法的求解质量和收敛速度有非常大的影响,求解柔性作业车间调度问题是为工序排序及每道工序选择最佳机器,各工序排序影响着机器的选择。

根据柔性作业车间调度问题的特点,本文提出了贪婪初始化的初始化方法,生成局部最优的初始种群,贪婪初始化工序排序部分采用随机生成的方式,机器选择部分按照工序排序顺序为每道工序选择当前完工时间最短的机器。具体执行步骤如下:

(1) 设置整数组tMP、tJP及参数k,tMP为机器{M1,M2,…,Mm}对应的紧前工序完工时间,tJP为工件{J1,J2,…,Jn}对应的紧前工序完工时间,初始化数组tMP、tJP中每个元素值为0,参数k=1。

(2) 随机生成一条工序排序部分染色体OS。

(3) 为OS[k]即工序Oij选择机器。将工序可选择加工机器集Mij对应的机器紧前工序完工时间tMP分别与该工件紧前工序完工时间tJP[i]进行比较,较大的为工序在对应机器上开始时间,开始时间加上机器的加工时间为工序在机器上的完工时间;选择完工时间最短的机器m作为当前工序的加工机器;若最小完工时间不唯一,则在完工时间最小的机器中任选,然后按照编码方式,记录在染色体相应位置。

(4) 将工序Oij完工时间作为被选择机器m的紧前工序完工时间更新到tMP[m]上,作为对应工件i的紧前完工时间更新到tJP[m]上。

(5) 循环执行步骤(3)～步骤(4),直到按工序排序顺序为所有工序选择加工机器。

贪婪初始化的流程如图2所示。

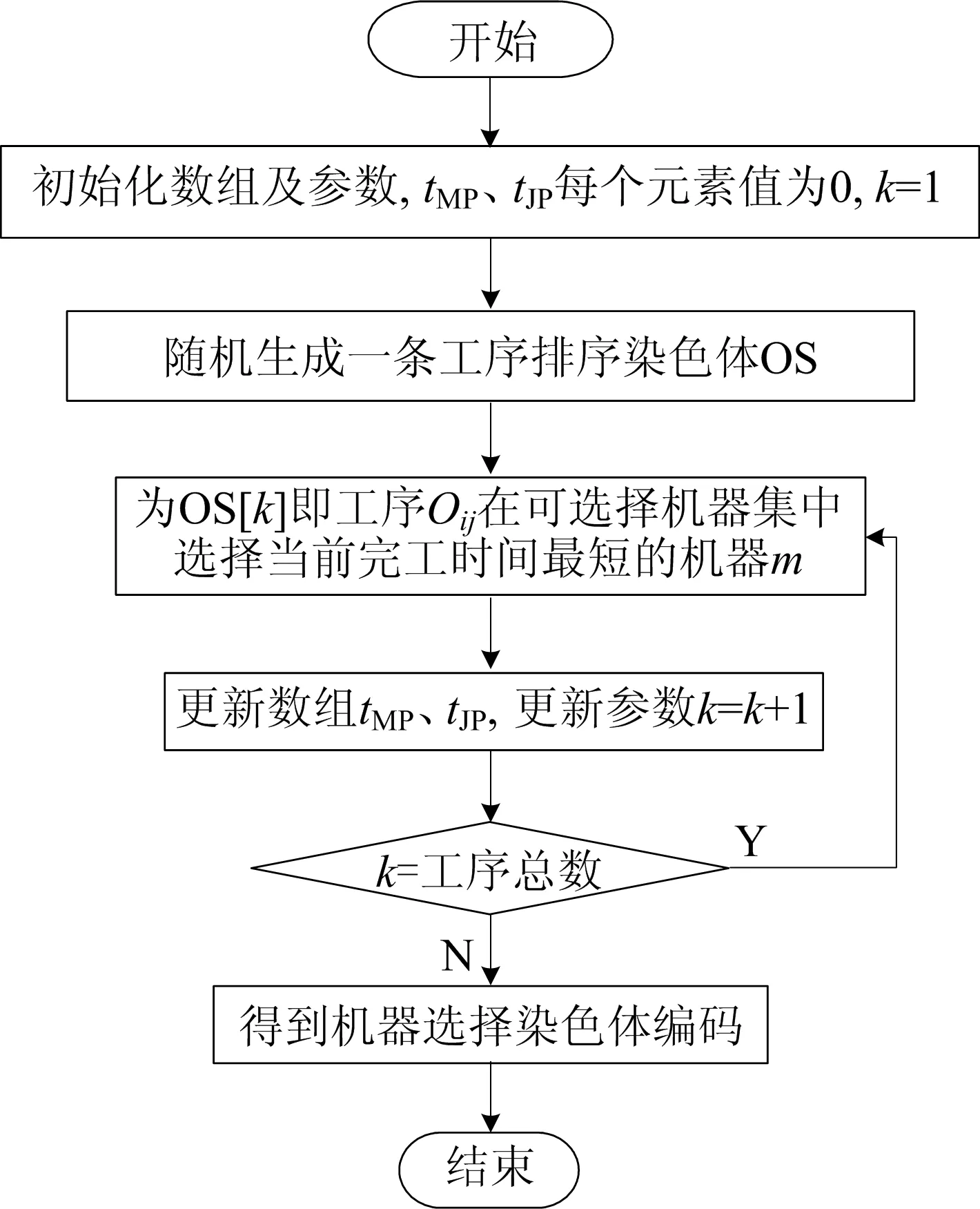
图2 贪婪初始化流程

2.3 遗传算子

2.3.1 选择算子

本文采用轮盘赌选择策略比较个体的适应度值,选择适应度值较小的个体作为交叉的对象,淘汰适应度值低的个体。为了保留高质量的解,提高收敛速度,在选择操作中引入精英保留策略。考虑到保留的解的多样性,在进行选择操作前,进行种群多样性筛选及初始化种群替换,将种群按照适应度值从低到高进行排序,按顺序选择第1个个体,将该个体机器选择部分染色体每个基因位上的值与其他个体进行比较,筛选出种群中机器部分染色体与其相同的个体,重复以上步骤按顺序遍历种群中所有个体,最后,采用初始化方法生成新的解对筛选出的个体进行替换。

2.3.2 交叉算子

交叉操作是通过重组基因段产生新个体的。本文染色体编码由2个部分组成,根据柔性作业车间调度问题的特点对2段编码采用不同的交叉方式。

工序排序染色体采用基于工序顺序的交叉(precedence operation crossover,POX)能够生成有效解,并继承父代的优良基因。在该操作中,将工件分为工件集1和工件集2,选取父代P1、P2并将P1、P2中工件集1的基因分别复制到C1、C2中的相同位置,然后将P1、P2中工件集2的基因分别按P1、P2中的顺序依次填充到C1、C2中空余的基因位上,得到2个子代染色体C1、C2。

机器选择染色体采用多点交叉,该操作为随机生成一条与机器染色体长度相同的基因为0、1的染色体C,选取父代P1、P2保留父代染色体与染色体C基因为1的位置相同的基因,交换父代与染色体C基因为0的位置相同的基因,得到2个子代染色体C1、C2。

2.3.3 变异算子

变异操作能维持种群多样性,对2段编码采用不同的变异方式。

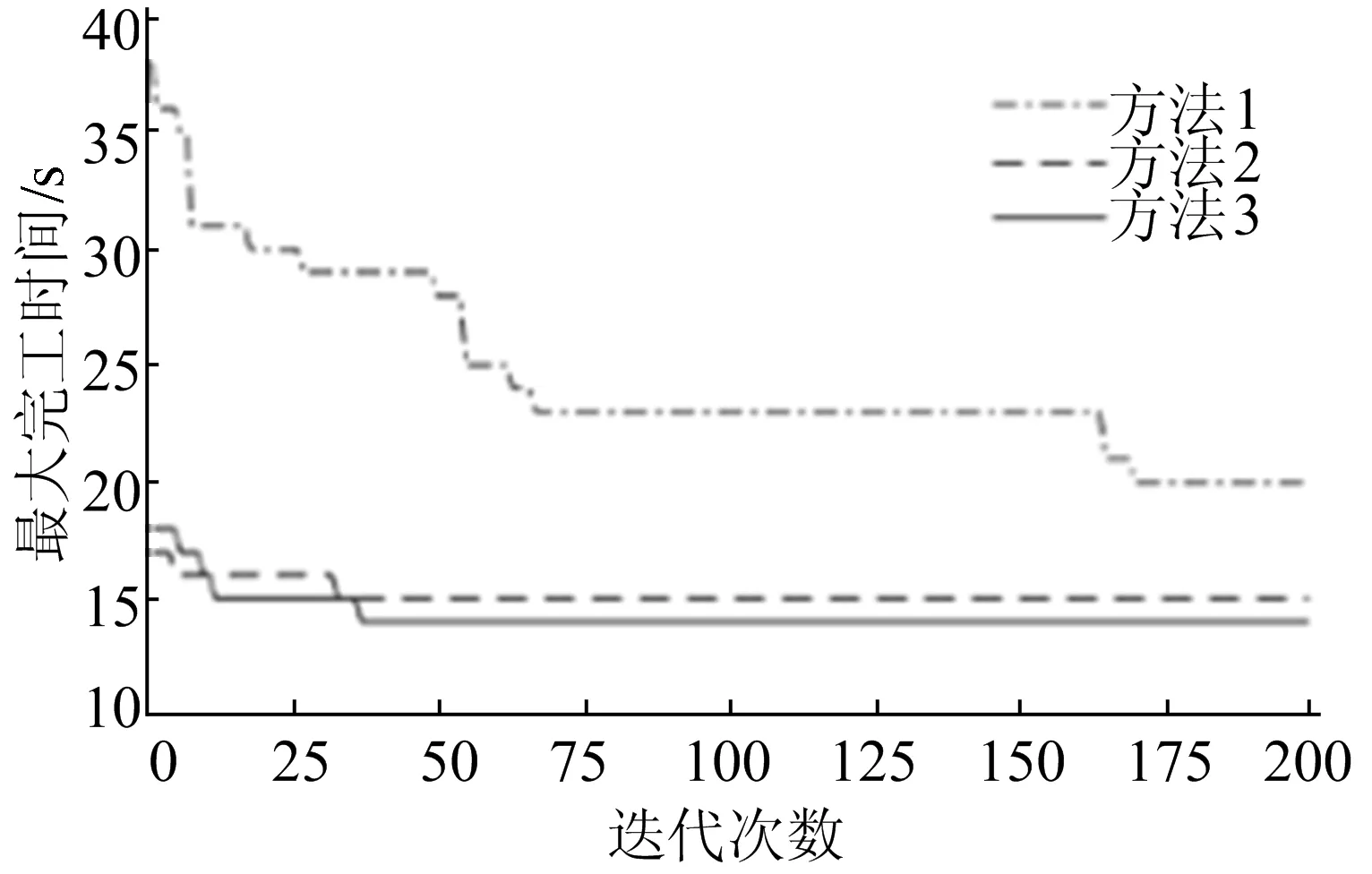
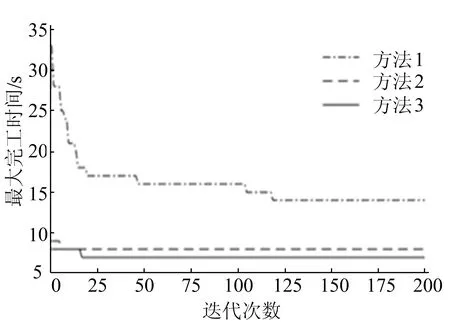
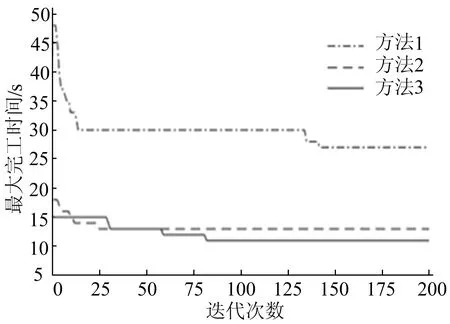
工序排序染色体采用位置变异,选取父代P,随机生成一条与工序染色体长度l相同的的染色体a,其基因为(0,1)之间的实数。若a(i)

机器选择染色体采用单点变异,选取父代P,随机生成一条与工序染色体长度l相同的的染色体a,其基因为(0,1)之间的实数。若a(i)

3 实验结果与分析

为了验证算法的可行性和有效性,本文选取文献[7]提出的柔性作业车间调度3个基准实例(8×8、10×10和15×10)进行求解,利用Matlab R2016b实现上述算法,并与文献[12]提出的改进人工蜂群算法(artificial bee colony,ABC)、文献[13]提出的改进遗传退火算法(enhanced genetic and simulated annealing,EGSA)、文献[14]提出的混合蜂群算法和文献[15]提出的结合DBR理论与改进遗传算法的DBRGA算法等对相同算例计算的结果进行比较。比较结果见表2所列。其中：Cmax为文献中求得的最大完工时间的最优结果;Aver为运行10次结果的平均值。

表2 文献[7]算例优化结果的对比

由表2可知：对于Cmax,本文提出的改进遗传算法与其他4个文献算法求解8×8、10×10、15×10问题都取得了的最优结果;对于Aver,本文算法求解3个问题的Aver比文献[12]和文献[13]算法求解的结果更优,本文算法求解的稳定性较好;对于CPU时间,本文算法3个问题运行的CPU时间比文献[13]、文献[14]和文献[15]算法给出了CPU运行时间短,本文改进算法在计算速度上更快。

测试本文中提出的改进遗传算法规避局部最优的有效性。将本文算法与采用随机产生和文献[8]初始化方法的传统遗传算法进行对比,8×8、10×10和15×10问题迭代200次的收敛对比图如图3所示。其中：方法1为随机初始化的遗传算法;方法2为采用文献[8]初始化方法的遗传算法;方法3为本文提出的采用贪婪初始化的改进遗传算法。

(a) 8×8问题

(b) 10×10问题

(c) 15×10问题图3 8×8、10×10和15×10问题的收敛对比结果

采用方法1与方法2求解3个问题，经过200次迭代运算后未求得全局最优解,算法陷入局部最优,而方法3能很快地跳出局部最优求得全局最优解。结果表明,本文提出的改进遗传算法可以有效地规避局部最优。

4 结 论

作业调度是生产计划实施过程中的重要环节,本文以最小化最大完工时间为目标,提出一种贪婪初始种群的遗传算法对柔性作业车间调度问题进行求解。采用了贪婪算法初始化,提高种群初始解的质量;设计了一种结合种群多样性筛选及初始化种群替换的选择操作,有效地规避算法陷入局部最优;最后使用Matlab工具实现本文算法对文献[7]基准实例的求解,并将所得的结果与其他文献的优化结果进行比较。结果表明,本文算法在求解柔性作业车间调度问题上稳定性高、收敛速度快,算法是可行的和有效的。