基于元动作的铣齿机机械结构可靠性评估

刘 赛, 姚 凯, 王 华, 洪荣晶

(南京工业大学 机械与动力工程学院,江苏 南京 210009)

数控铣齿机床是用于加工高精度齿轮的大型机械设备,广泛应用于工程设备、冶金装置、风电设施等工业领域。数控铣齿机床的机械结构作为功能实现的主要载体,其可靠性至关重要。在进行此类大型设备机械结构分析中,往往会面临以下问题: ① 大型设备机械结构复杂、零部件数量繁多、存在多种耦合作用影响导致分析困难; ② 传统的可靠性研究方法主要研究电子设备故障,在应用到机械结构中有所不足,同时传统可靠性分析往往忽视故障溯源问题,对故障产生根本原因的分析存在不足。

针对问题①,本文引入元动作理论,用以细化故障分析的粒度,将复杂繁多的零件结构简化成元动作进行运动分析,便于更快确定目标对象。元动作理论对机械系统结构分析的适用性使其在机械产品的可靠性分析中得到广泛的应用。文献[1]将元动作理论用于装配单元及误差传递模型分析,简化装配单元分析粒度提升了传递误差分析精度;文献[2]基于元动作理论研究出一种适用于数字孪生的运动研究模型;文献[3]将元动作运用于动态特性研究分析,用以消除分析中耦合作用因素的影响;文献[4]将元动作用于柔性制造系统的动态分析,优化了整体模型分析结构。

针对问题②,众多学者对传统的可靠性研究方法加以改进优化。文献[5]将多标准决策方法与灰色理论应用于故障模式与影响分析(failure mode and effects analysis,FMEA),改善了FMEA实际应用中的诸多缺陷;文献[6]将模糊MOORA与FMEA结合,用以优化多目标分析以及风险决策的不足;文献[7]将直觉模糊MULTIMOORA引入FMEA中,优化了风险评估中评估信息不确定、风险值计算模型不合理的问题;文献[8]引入基于模糊证据推理用以评价信息的模糊化,并用改良的灰色关联度优化FMEA排序模型。

本文引入元动作概念,提出一种基于元动作的铣齿机机构的可靠性评估方法。基于元动作理论,建立数控铣齿机床功能-运动-动作(function-movement-action,FMA)模型,运用模糊TOPSIS(technique for order preference by similarity to an ideal solution)方法对传统FMEA分析中评估信息的不确定性和传统RPN计算模型中相同风险值难以排序的问题进行优化,运用故障树贝叶斯网络方法，改善传统故障树在处理不确定性问题上的不足,提升了铣齿机机械结构的可靠性评估水平。

1 元动作理论

1.1 元动作相关概念

元动作是机械产品中传递运动与动能的最基本的运动形式,而实现元动作的结构单元通常定义为元动作单元[9]。一个基本的元动作单元往往由输入部分、中间件以及输出部分3个部分组成。输入部分代指动力输入,往往有电机输入或者上一级输出所得;中间件为元动作单元中起到紧固、定位、支撑功能的零件;输出部分指的是动力输出,主要将运动、动力传递到下一元动作单元。

FMA结构化分解是一种以“功能-运动-动作”为分解路线,由此将整机分解至不可再分的元动作的动作集合的结构分析方法。在进行对大型机械设备故障分析时,通常需要对其进行分解来简化分析难度,将整机系统拆分为多个子系统,然后再进一步细化,直接分解到不可分部分。

本文采用FMA分解方法对铣齿机进行分析时,将元动作层作为系统分解额最小分层量,与传统的零部件作为分析底层有着很大区别。

1.2 元动作单元故障定义

元动作单元为实现元动作的结构单元,参考元动作定义,将元动作故障定义为产品运行过程中运动单元无法完成预期功能的现象。结合实际生产中故障现象,将元动作单元的故障分为运动类与连接类2类。运动类指的是元动作单元在生产过程中自身运动的问题,包括精度、稳定性、协调性此类问题;连接类指的是元动作结构中的连接单元的问题,例如堵塞、断裂等。

总结归纳数控铣齿机床的元动作单元故障现象,结果见表1所列。

表1 元动作单元故障模式类型

2 元动作单元故障模式排序技术

在进行系统可靠性分析时,需要寻找关键部位确定关键原因。在进行元动作故障模式及影响分析后,需对其进行风险评估排序以确定故障模式优先级。

本节将模糊理论与TOPSIS排序方法相结合应用,传统FMEA分析中专家评估信息往往都是整数形式,这并不符合实际分析情况,采用模糊化有利于扩大评估范围,提高评估结果的精确性,使用三角模糊数方法对评估因素进行模糊化处理,结果见表2、表3、表4所列。

表2 严酷度等级S

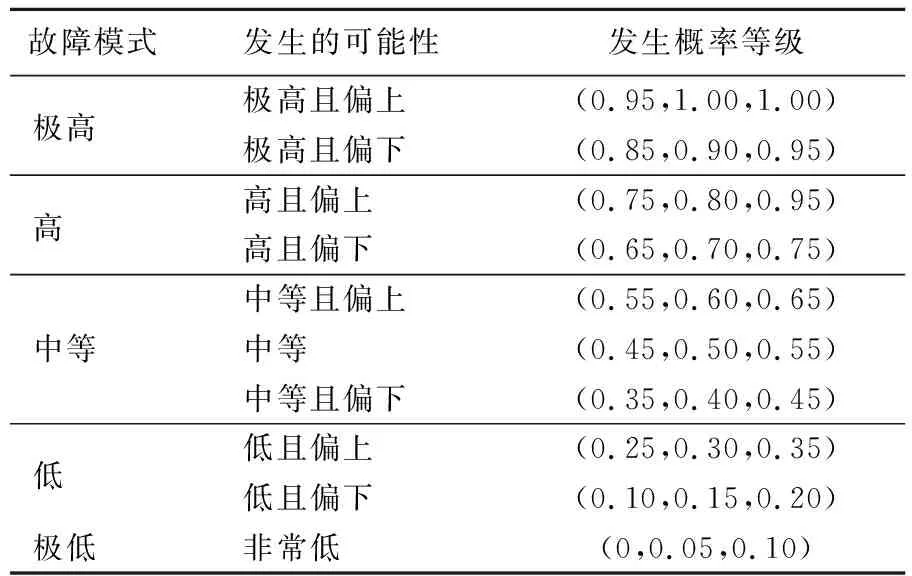
表3 发生概率O

表4 检测难度等级D

TOPSIS方法是一种应用于多目标决策分析的算法,通过构建整体分析对象的正、负理想解,计算评估方案到正、负理想解的距离来确定方案优先级[10]。TOPSIS方法具体流程如下所述。

(1) 建立决策矩阵。第1步涉及到的是建立多属性决策矩阵A=(aij)m×n,通常需要进行一个数据预处理以获得一个规范化的决策矩阵B=(bij)m×n。数据必须预处理的原因包括：① SOD 3个属性具有不同的类型,因此无法直接从属性值判断各方案的优先级; ② 每个属性值测量单位不同;③ 不同属性值的差值较大。通常采用文献[11]中规范化决策矩阵方法进行数据预处理,即

(1)

其中:i=1,2,…,m;j=1,2,3。

(2) 建立加权规范化决策矩阵。在评估分析中,评估属性的权重往往并不相同,考虑评估属性的权重ωj,可以得到加权规范化决策矩阵C=(Cij)m×n,即

Cij=ωjbij

(2)

其中:i=1,2,…,m;j=1,2,3。

(3) 确定正、负理想解C+、C-。则有:

其中:J为效益型属性,数值越大效益越高,数值越小效益越差;J*为成本性属性,数值越大成本约高,数值越小成本越小。

(4) 计算方案到正、负理想解的距离,即

(3)

(4)

(5) 确定方案的优先级。综合指标评估按照以下公式进行:

(5)

最后按照指标计算值完成相关的排序以确定优先级。

3 故障树贝叶斯网络模型

贝叶斯网络是一种基于贝叶斯条件概率和图形理论的概率推理网络,由节点与定向边构成[12]。其中节点代指随机变量,圆弧代指变量间的因果关系。使用根节点的先验概率以及非根节点的条件概率表示随机变量间的相关性大小。一般条件概率往往是由Bayes定义公式推理得出。假设给定变量B,那么A的条件概率为:

P(A|B)=[P(A)P(B|A)]/P(B)

(6)

在贝叶斯网络中,假定G=(I,E)为一有向无环图,I为节点的集合,E为有向边的集合,且令X=(Xi)i∈I表示其以节点i所代表的随机变量,则X的联合概率密度分布可表示为:

(7)

在贝叶斯网络的结构学习中,故障树-贝叶斯网络转化法已经是一个较为流行、较为成熟的方法体系。通过比较贝叶斯网路结构与故障树分析 (fault tree analysis,FTA)法结构,可以发现两者之间的组成结构是相类似对应的。FTA法主要由各层事件与逻辑门组成,贝叶斯主要由各层节点及有向弧与条件概率表组成,两者方法结构的相似性意味着两者可以相互转化。具体的转化关系如图1所示。

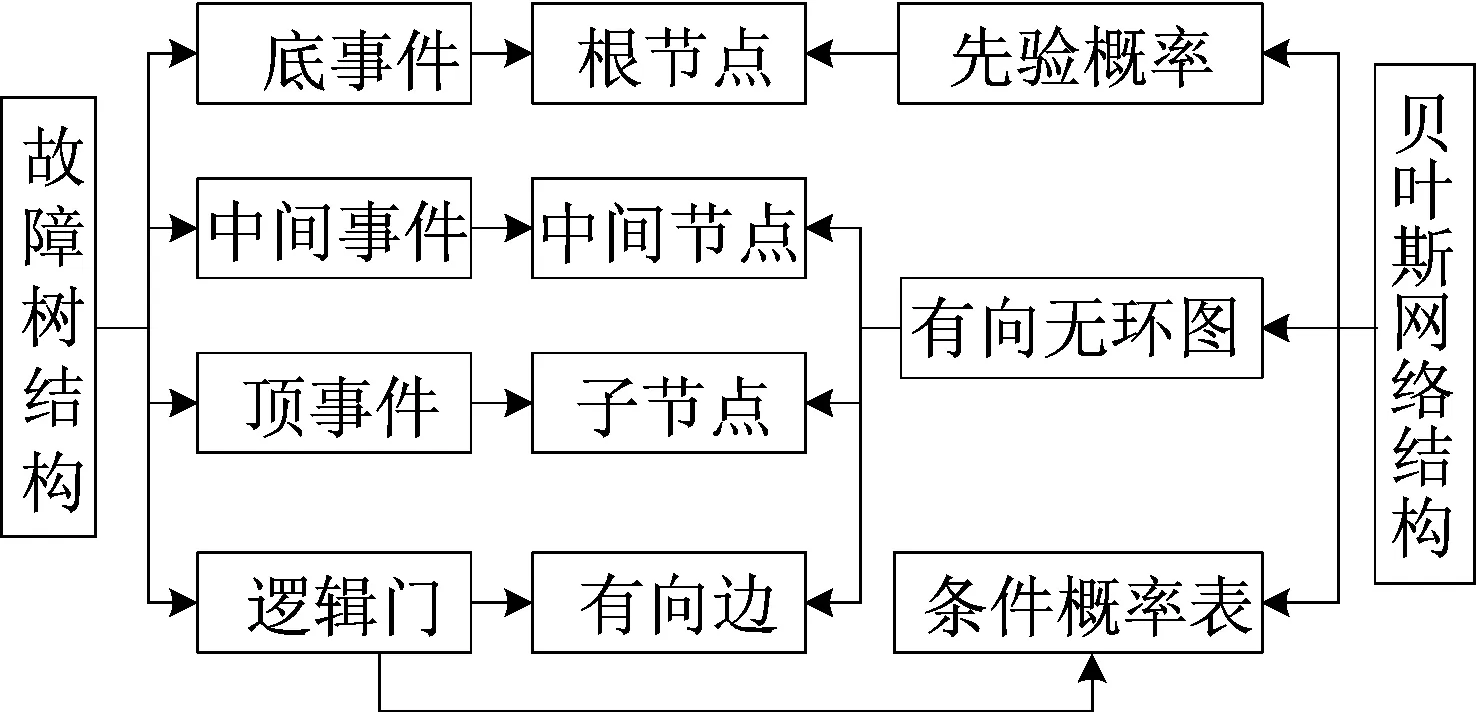
图1 故障树贝叶斯网络转换对应关系

4 实例分析

本节将采用优化方法对数控铣齿机床进行案例研究分析。该数控铣齿机床的故障数据由某数控有限公司提供,该故障数据包括研制阶段同类铣齿机产品的故障数据以及产品用户公司的数据。

首先对数控铣齿机床进行FMA结构化分解,结果如图2所示。通过对机械系统的分解,一共分解出28个元动作。

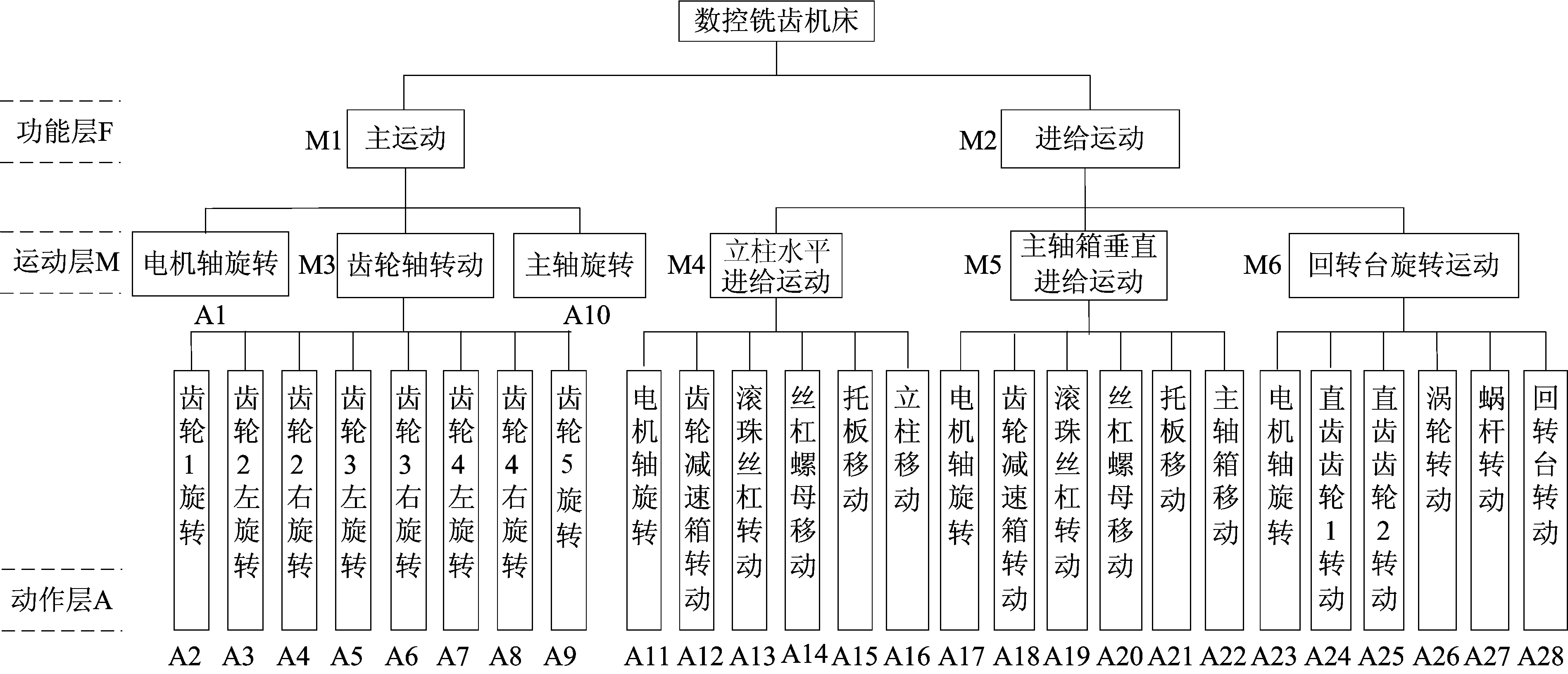
图2 数控铣齿机床FMA结构化分解模型

结合数控铣齿机机床特点与设计专家的工程经验、知识,确定本例中评价指标的权重为ω=[ω1ω2ω3]T=[0.5 0.3 0.2]T。

考虑到元动作单元的数量过多,选取X轴立柱进给运动进行详细分析,通过FMEA分析得到了X轴立柱进给元动作单元的故障模式以及加权规范决策评估矩阵,其具体结果见表5、表6所列。

表5 元动作单元故障模式

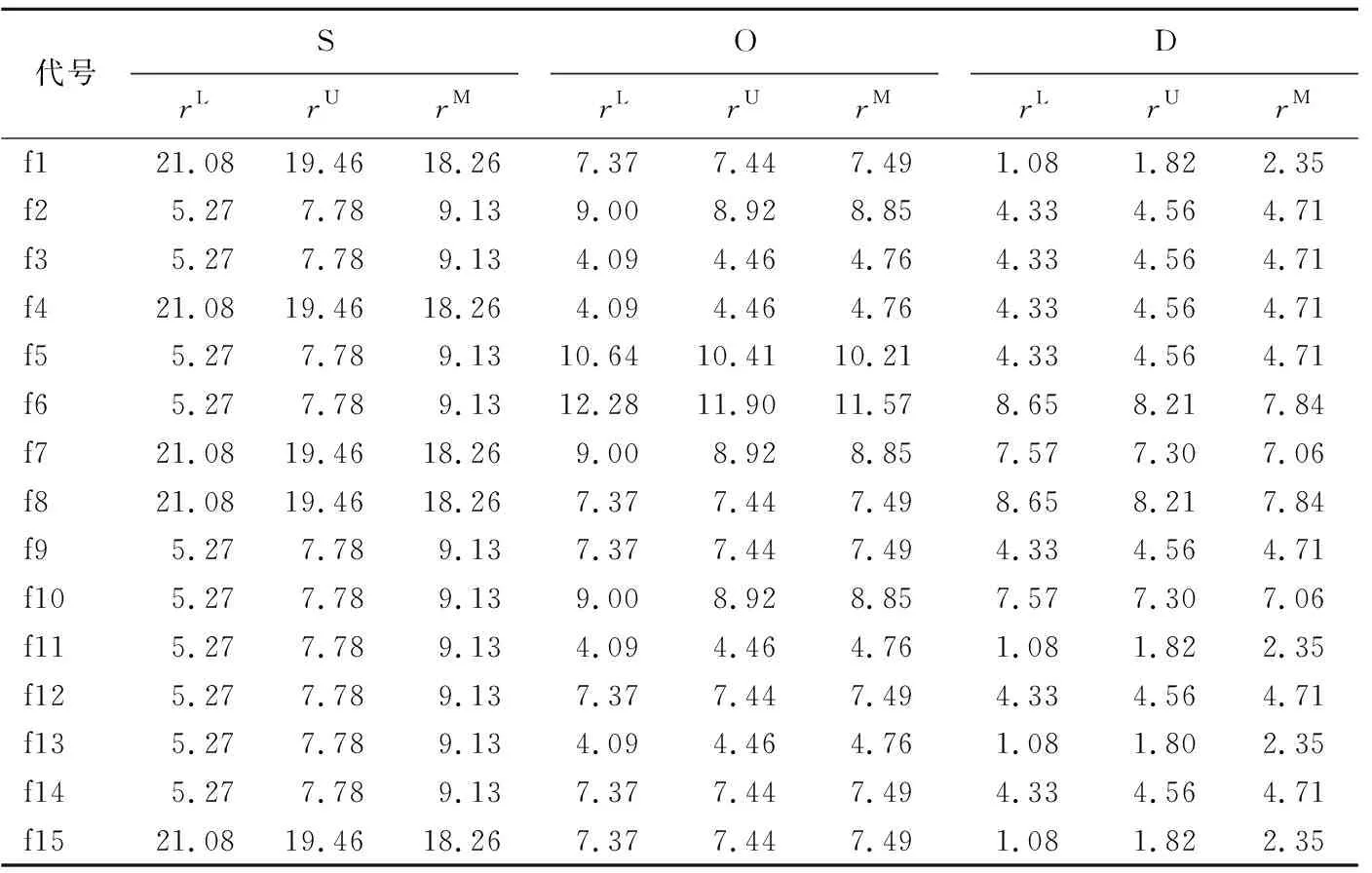
表6 加权规范决策矩阵 单位:10-2

计算正、负理想解为:

C+={(21.08,19.46,18.26),(12.28,11.90,

11.57),(8.65,8.21,7.84)};

C-={(5.27,7.78,9.13),(4.09,4.46,4.76),

(1.08,1.82,7.84)}。

计算每个故障模式正、负理想解的距离为:

14.51, 22.76, 21.67, 5.44, 7.79, 23.92,

22.34, 27.69, 23.92, 27.69, 23.92, 13.74);

22.21, 11.47, 17.24, 25.00, 25.00, 7.12,

12.45, 0.01, 7.12, 0.01, 7.12, 22.29);

(S1,S2,…,S15)=(0.618 6,0.283 6,0.157 0,

0.604 9,0.335 1,0.443 0,0.821 2,0.762 4,

0.229 3, 0.357 9, 0.000 3, 0.229 3, 0.003,

0.229 3, 0.618 6)。

根据上述相对贴近度的计算结果,可以得到数控铣齿机元动作单元故障模式的排序结果为:

Sf7>Sf8>Sf15≥Sf1>Sf4>

Sf6>Sf10>Sf5>Sf2>Sf9≥

Sf14≥Sf12>Sf3>Sf13≥Sf11。

综合模糊TOPSIS方法的排序结果以及研发设计人员的设计考虑,选取排名前三的故障模式作为关键元动作单元故障模式,发现这些故障模式均属于滚珠丝杠转动单元、立柱单元故障模式,且比其他元动作单元的故障占比更大,因此在后续进行可靠性优化分析时应重点考虑。确定关键故障模式后,将利用故障树贝叶斯分析方法对其作进一步分析,找出关键故障原因。

下面以滚珠丝杠转动元动作失效为例进行分析。

滚珠丝杠在铣齿机机械结构中作为X轴、Z轴进给运动中的主要结构单元,其性能稳定性直接决定了铣齿机最终工作效果。现以丝杠转动元动作单元失效作为顶事件进行故障树分析,具体如图3所示。

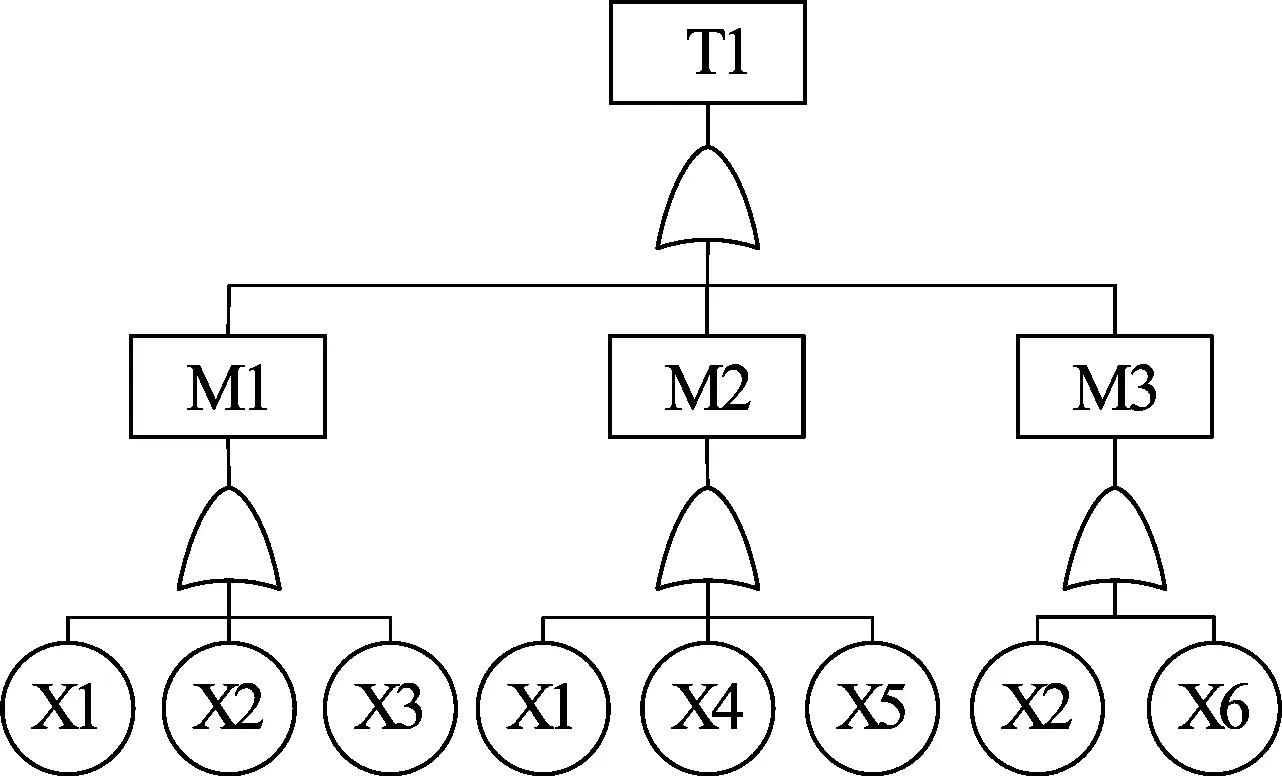
图3 丝杆转动元动作失效故障树

滚珠丝杠转动元动作单元失效故障树事件定义见表7所列。

表7 元动作单元故障树事件定义

根据研发阶段数据以及后续产品调研所得结果,可以得到底事件故障率,见表8所列。将底事件故障率作为先验故障率输入,可以得到故障率fPT3=0.72%。

表8 底事件故障率

依照贝叶斯网络进行构建,结果如图4所示。依据贝叶斯网络的双向推理能力,将滚珠丝杠转动失效事件fPT1=1作为事件输入,得到的结果图5所示,可以判定滚珠丝杠转动元动作失效的关键原因是丝杠磨损以及润滑问题,在后续的分析中应优先考虑。

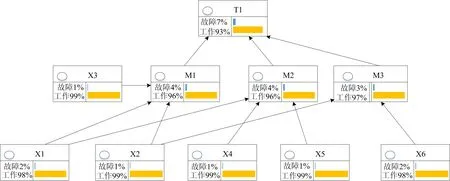
图4 滚珠丝杠转动失效贝叶斯网络

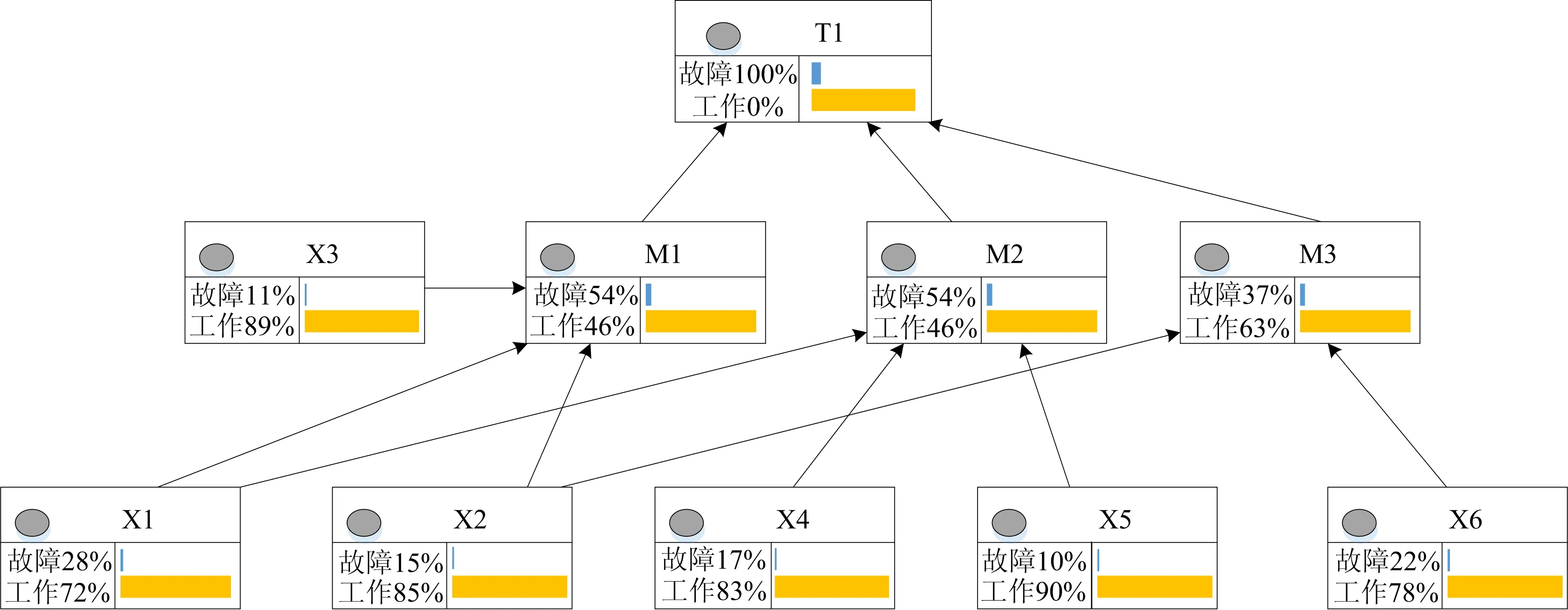
图5 滚珠丝杠转动失效反向推理图

故障树贝叶斯网络的运用,使得对于机械结构可靠性分析有了进一步的提升,能更快找到故障关键原因,优化了故障分析能力,提升了可靠性评估水平。

5 结 论

大型设备机械结构的可靠性正愈发得到重视,传统的故障分析方法又有所局限,针对这一情况,本文提出了一种基于元动作的铣齿机机械结构故障分析方法。引入元动作构建FMA结构化分析模型,结合模糊理论与贝叶斯理论,对传统可靠性分析方法加以改进,使其能够对铣齿机机械结构进行有效合理的分析。该方法具有以下优势:

(1) 层次结构清晰。在进行机械系统分析时,按照方法能轻松一步一步执行,逐层分析,确定最终原因。

(2) 机械结构的适用性。引入元动作理论这一更适合机械系统的分析方法,简化了分析粒度,降低了分析难度。

(3) 对传统的可靠性分析方法进行改进。运用模糊TOPSIS方法对FMEA风险排序加以改进,利用故障树贝叶斯解决了FTA在处理不确定问题上的不足。

最终经过实例应用证明了本文铣齿机机械结构可靠性评估方法的可行性。