正交设计和响应面设计在路用混凝土配合比优化中的应用与比较
2021-09-30张丽娟孟昕娜
张丽娟, 孟昕娜
(石家庄铁道大学 四方学院基础部,河北 石家庄 051132)
0 引言
试验设计(DOE)是现代应用数学中的一部分,也是试验优化的重要方法。Fisher[1]第一次使用试验设计方法在农业生产中进行试验优化后,其应用范围逐渐扩大。DOE以数理统计的相关理论知识为基础,根据研究需要,力求用较少的试验次数来获得比较可靠的试验数据,然后通过数据分析得出具体的结论。如果试验过程中设计合理,就能事半功倍;相反,耗时耗力,还可能导致试验失败。因此,能否合理进行试验设计,已经成为科研工作的关键。目前正交设计的应用较为广泛,但其他设计方法工程技术人员也一直在探索。
龙菊等[2]采用正交试验和响应面试验研究微波纤维素酶法提取山药多糖的影响因子和水平,来进一步优化制备工艺,表明与正交试验相比,响应面设计不但可以直观展现各因子的交互作用,而且在结果准确性方面也更加合理。蔡厚道[3]同时采用正交设计和响应面设计对影响装配尺寸的因子进行优化,表明响应面设计的最优工艺精度更高。刘炬灼等[4]通过正交设计和响应面设计优化五味子的炮制工艺,表明响应面设计比正交试验设计得到的总木脂素含量要高,而且能得到更多更精确的信息。刘强等[5]采用Box-Behnken中心组合设计对影响砂浆粘结强度的因子及其性能预测,表明建立的二元回归模型在拟合区间内拟合程度很好,为砂浆性能的优化提供了一种新的研究方法。牛江川等[6]采用正交设计对影响盾构刀具磨损的参数进行分析并建立相应的模型。王喜盈等[7]基于正交设计对影响钢-混凝土双面组合连续箱梁剪力滞效应的影响因素进行设计分析,并建立相应的无量纲计算公式。张军等[8]基于响应面设计进行船撞桥的可靠度分析,通过对比蒙特卡洛法证明了响应面法的有效性和高效性。
由上述应用可以看出,不同领域研究人员基于所学知识应用的试验设计的方法差异性大,在结构混凝土设计中,影响其性能因素众多,如混凝土配合比、养护制度、搅拌方式等,更为重要的是性能评价是以养护28 d或更长龄期为基准,这样多影响因素高龄期的试验设计在其他工程领域很少遇到,故合适的试验设计尤为重要。但目前常用的是单因素设计或正交设计,而效率和精度更高的响应曲面法因数理统计相关知识要求更高所以应用较少,故从正交和响应面关键设计要点介绍入手,以基于目标性能的路用混凝土配合比优化设计为例,对比2种方法的相关数理统计知识、差异和精度,以期提高科研和工程技术人员试验设计的科学性和效率。
1 设计方法
1.1 正交设计的原理和设计方法
正交设计方法[9]是借助正交表进行试验设计并对试验数据进行直观分析,最终达到以较少的试验次数获得可靠数据的目的。近年来广泛应用于化工、农业、医学、环境和工程学等领域[10-12]。在试验设计中,如果每个因素的水平组合都考虑到就是全面试验,全面试验耗时耗力,例如三因素三水平的全部试验点为33个,四因素三水平的全部试验点为34个。此时若从中选择几个代表性的试验点进行试验设计就可以显著缩减试验次数。三因素三水平正交试验就是从全面试验点中挑选出图1所示的9个代表性点,即正方体每个平面上选择3个试验点,这样就能够比较全面地反映整个区域内的基本情况。

图1 正交设计三因素三水平的代表性试验点图
正交试验的一般过程为:(1)确定因素水平和衡量指标。(2)绘制因素水平表。(3)选择正交表,其中正交表列数应大于因素数,比如图1的三因素三水表应选择L9(34)的正交表。(4)严格按照正交表设计的水平组合进行试验并记录相应的指标值。(5)数据分析。(6)验证,即如果根据数据分析出的较优条件在正交表中没有出现,则需按照该条件做一次试验来验证。
1.2 响应面设计的原理和设计方法
Box et al[13]提出一种可以同时进行试验优化和模型预测的试验设计方法——响应面法,它是对整个曲面内因素与指标之间的关系进行回归分析,根据模型进行优化和性能预测[14]。Weierstress的多项式最佳逼近定理表明,大部分函数关系都可以用多项式模型进行拟合,所以无论一个变量与响应值之间是怎样的函数关系,实际应用中都可以应用多项式模型拟合[15]。一般地,响应值Y与设计变量x之间满足
(1)
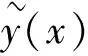
采用Weierstress的多项式模型近似逼近,则有
(2)
式中,φi(x)为基函数;βi为基函数的线性效应。
当部分因素水平值偏离曲面的最优位置时,常用一阶多项式模型近似逼近,即
(3)
当因素水平值接近或位于最优区域内时,常用二阶多项式模型近似逼近,得到最优因素水平组合,即
(4)
式中,βi、βii分别为xi的一阶、二阶效应;βij为xi与xj的交互作用效应。
绝大多数的RSM问题都可在一个较小范围内将复杂的函数关系表达为简单的一阶或二阶模型,借助最小二乘法近似计算多项式的参数。
响应面设计方法近年来已发展成为一种试验优化方法,众多学者对其进行了大量的应用研究[16-18]。响应面法的一般过程为:(1)析因分析,即筛选显著性因素。(2)试验设计,确定因素水平及响应值,借助软件进行试验设计,例BBD在试验设计中基础数据是12个,即以“0”为中心点,“+1”“-1”分别是立方点相对应的高值和低值,特别注意中心点处需要进行中心重复试验(不少于3组)来考察中心区域拟合情况,如图2所示。(3)严格按照设计方案进行试验,获得相应的响应值。(4)数据分析。
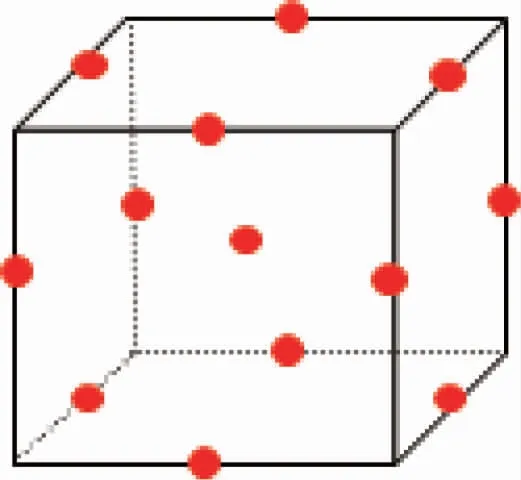
图2 响应面设计三因素三水平代表性试验点图
2 应用示例
路用混凝土除耐久性要求外,衡量其性能关键指标是其抗折强度。下面以路用混凝土抗折强度性能指标要求,对比分析正交设计和响应面设计在其配合比试验设计和性能优化方面的差异。在这里需要强调的是马士宾[19]认为砂率、粉煤灰和减水剂是影响混凝土路用性能的主要因素,故基于路用水泥混凝土配合比设计的有关经验[20-21]固定水灰比为0.38,分析这3个因素对抗折强度的影响。正交设计配合比见表1,响应面设计配合比见表2。

表1 正交设计配合比 kg/m3
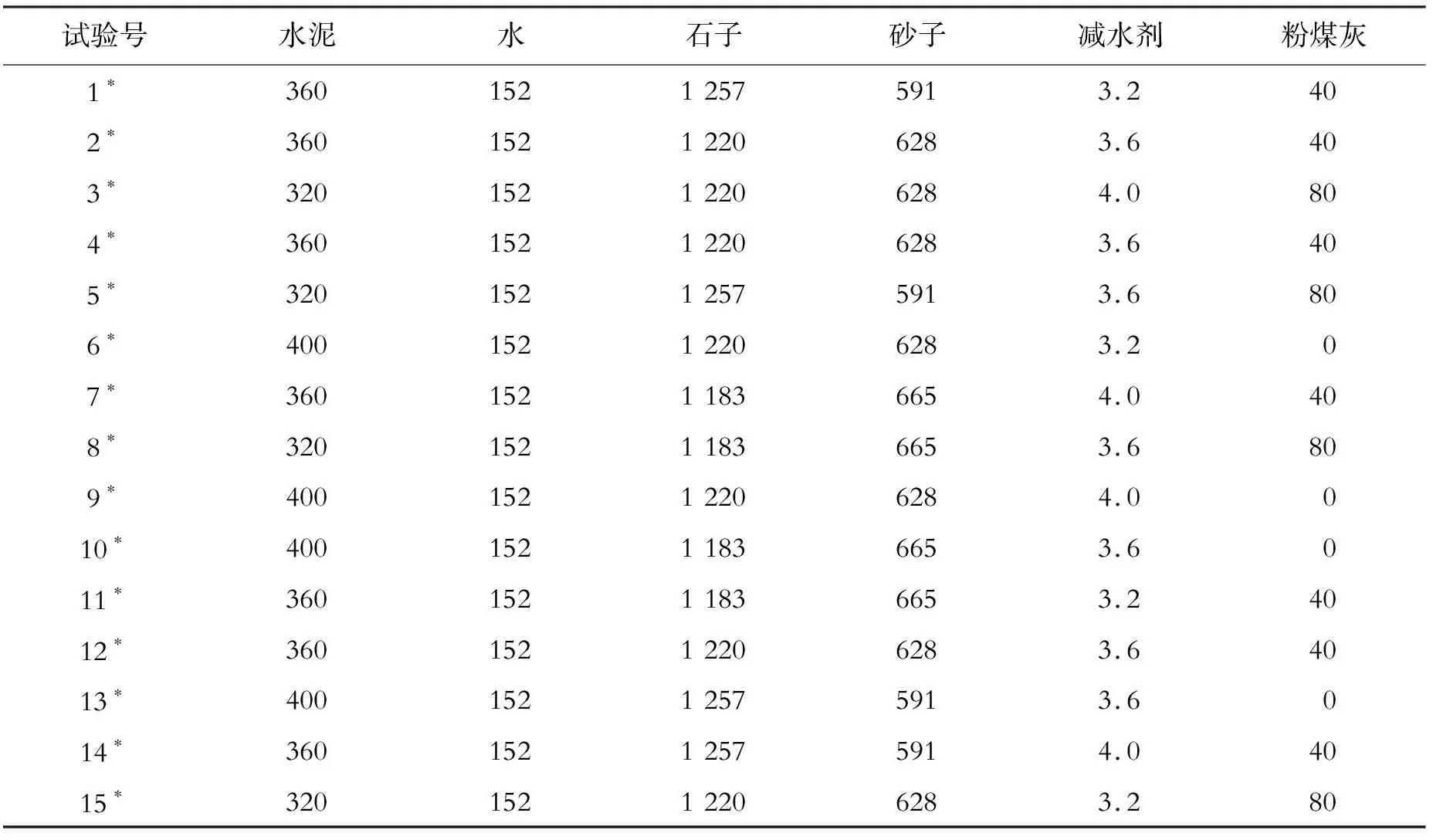
表2 响应面设计配合比 kg/m3
2.1 试验设计
以粉煤灰掺量、砂率和聚羧酸高效减水剂掺量为设计变量,以路用混凝土28 d抗折强度为衡量指标,正交设计和响应面设计的因素水平表分别见表3和表4。

表3 正交设计因素水平表

表4 响应面设计因素水平表
2.2 数据处理
正交设计的结果分析见表5和表6。结果表明:各主效应显著性排序为C>B>A;聚羧酸高效减水剂掺量对抗折强度的影响较为显著(F>F0.05),而粉煤灰掺量和砂率对抗折强度的影响较小。最佳的试验条件是A2B2C3,即最优工艺参数为粉煤灰掺量10%、砂率34%、聚羧酸高效减水剂掺量1.0%,此时的抗折强度达到6.0 MPa。
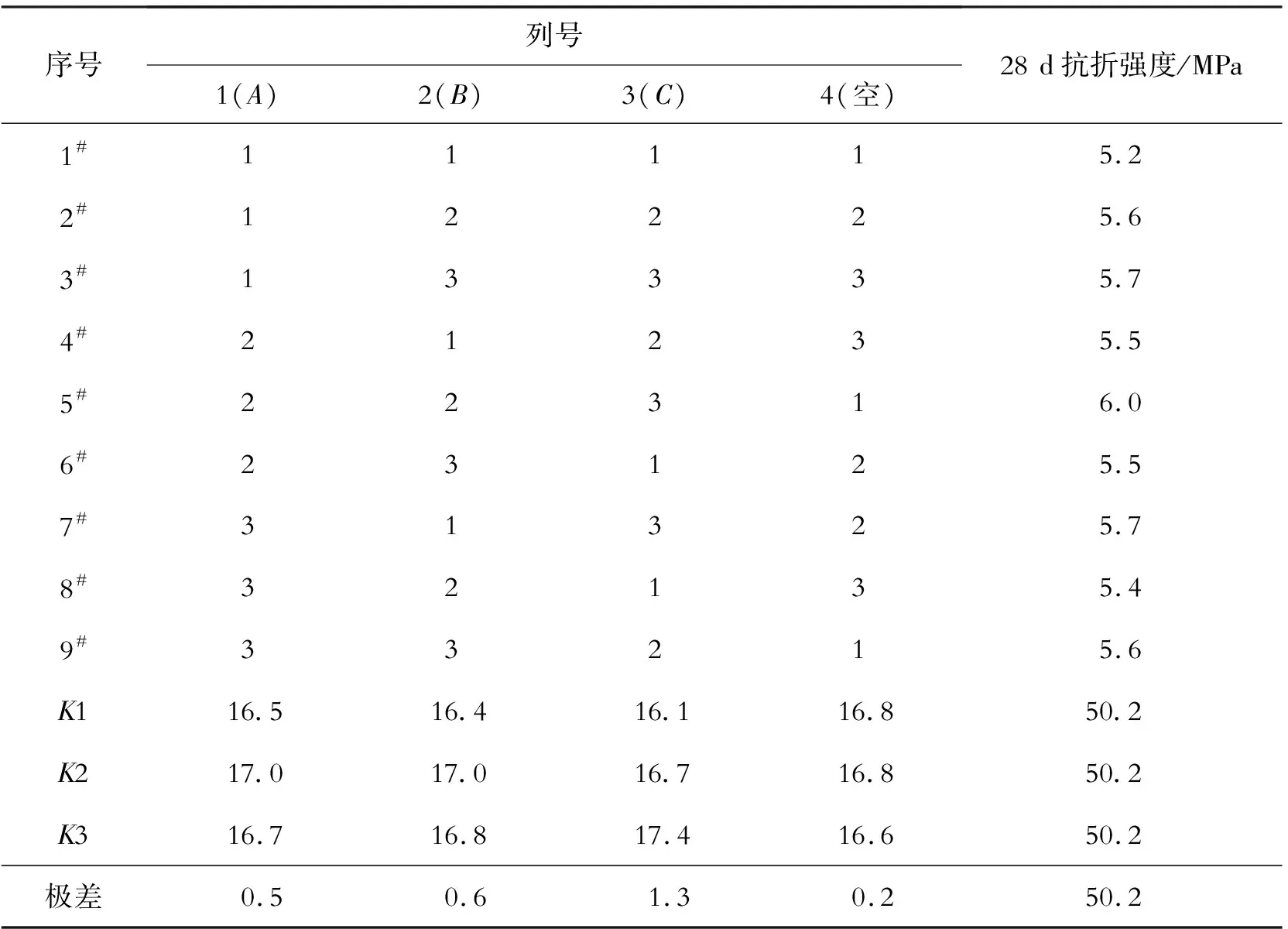
表5 正交设计结果分析表
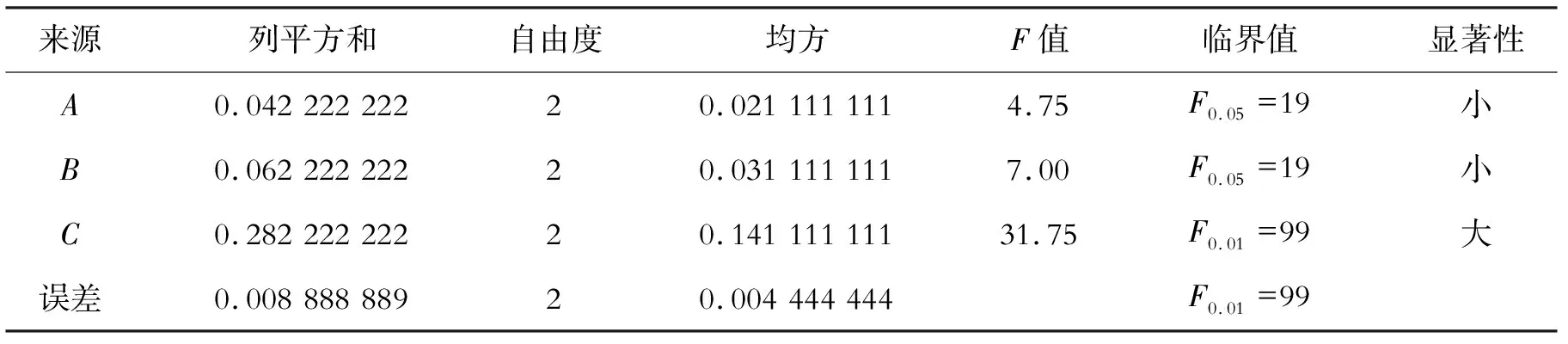
表6 正交设计方差分析表
通过以上数据处理的过程可以看出,正交试验分析的对象为离散型数据,即图1所示立方体上9个均匀分布的孤立点,试验次数少但布点均匀分散、整齐可比,从而避免了部分试验误差的干扰。在直观的极差和方差分析中体现了各因素(主效应)的最优水平值和显著性大小,但是获得的最优工艺参数只能是所选水平的某种组合,这也使试验结果的准确性降低。此外因素之间的交互作用在结果中并没有体现,这归因于正交表的选择,即在试验设计时就基于因素间不存在交互作用而选择的无交互作用列的正交表。正交表的选择决定了在试验设计前需要积累大量的专业知识和实践经验才能保证试验的准确性,因为一旦正交表选择错误,不但会对各效应的显著性产生影响,还可能会出现交互作用的混杂。
以粉煤灰掺量、砂率和聚羧酸高效减水剂掺量为设计变量,进行响应面设计的试验结果见表7,对结果进行分析并建立式(5)所示的二元回归数学模型。
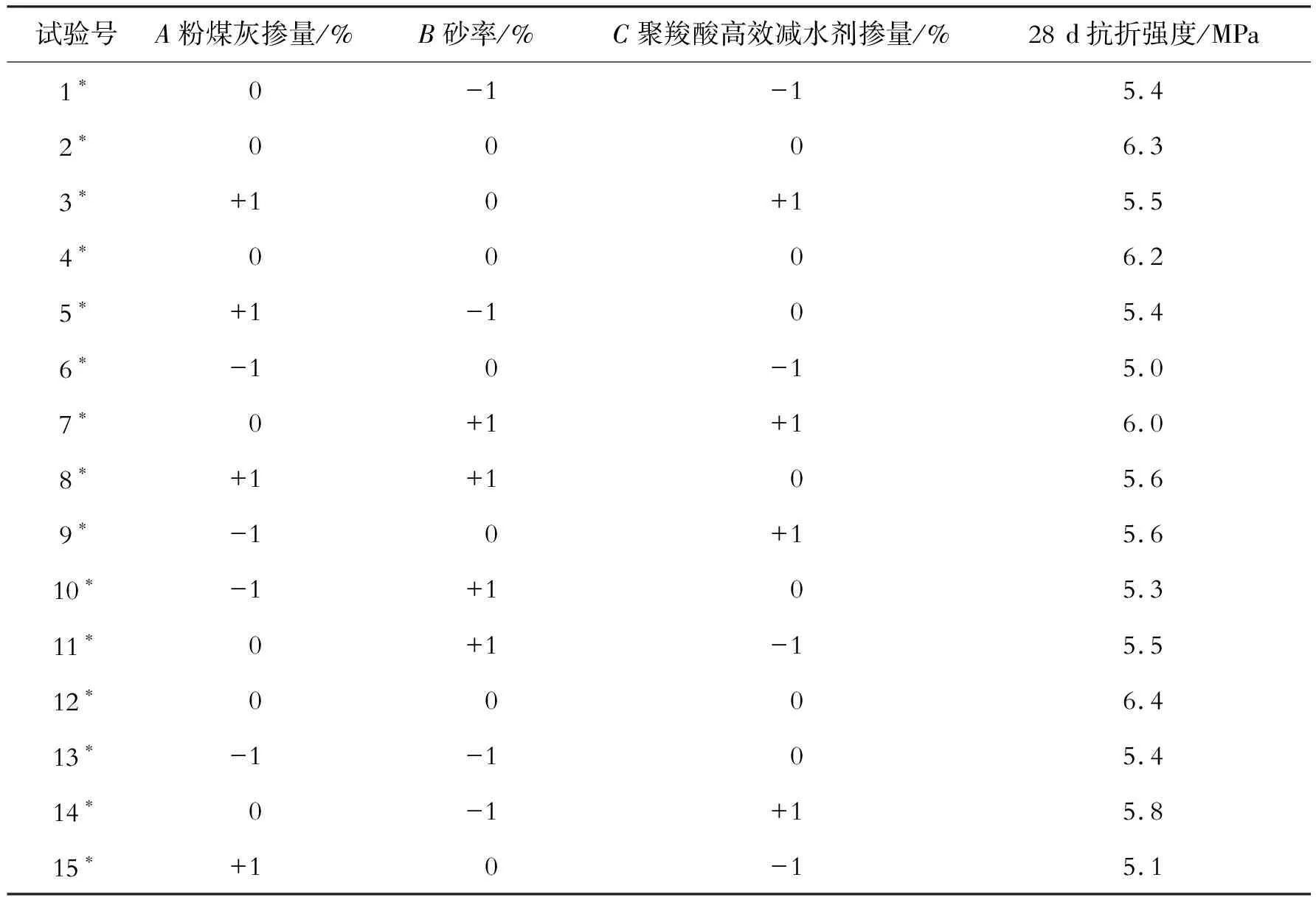
表7 响应面设计试验结果分析表
Y=-95.325+0.011 563A+4.125B+66.125C+9.375×10-4AB-0.012 5AC+0.125BC-3.906 25×10-4A2-0.062 5B2-37.5C2
(5)
该模型的方差分析结果见表8。从表8中可以看出模型的P<0.001,即建立的二元回归数学模型是极显著的;失拟项的P>0.05,即失拟项不显著;这2个值均说明建立的回归方程可以很好地预测抗折强度。根据P值可知,主效应中的减水剂掺量、曲面作用中减水剂掺量、粉煤灰掺量和砂率的平方项对抗折强度的影响比较显著,一次项显著性排序为C>B>A。
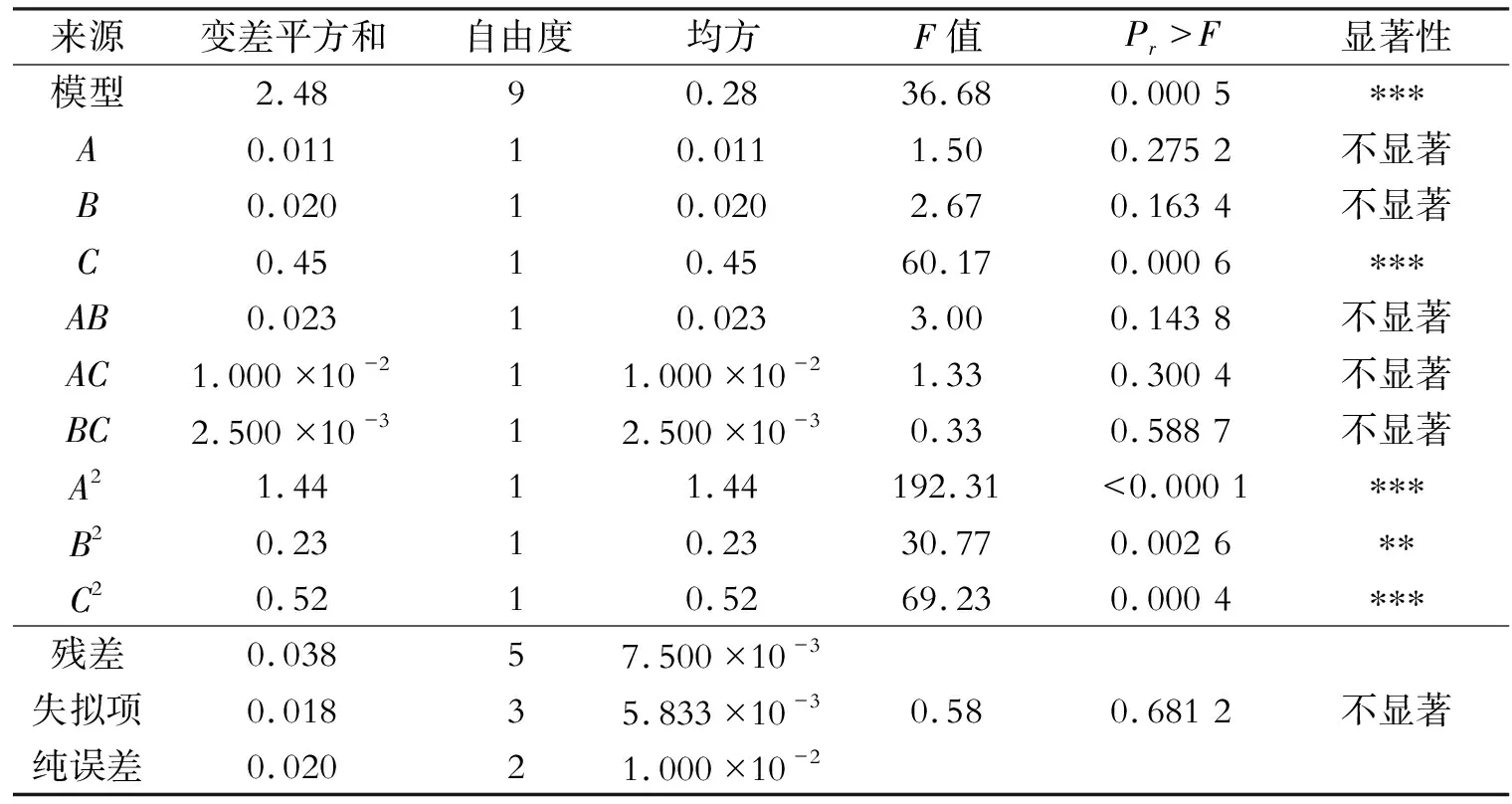
表8 响应面设计方差分析表
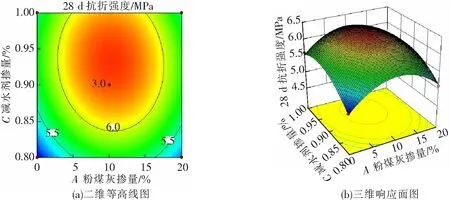
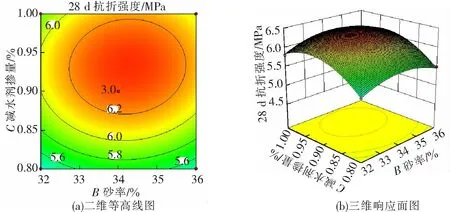
在某一因素固定为“0”水平的条件下,分析其他2个因素的交互作用对抗折强度的影响结果如图3~图5所示。二维等高线的形状越接近椭圆则表示因素间的交互作用越显著[22]。从图3~图5可以看出,随着砂率和粉煤灰掺量的增加,28 d抗折强度均出现先增大再减小的趋势且幅度较大,明显的椭圆状等高线也说明砂率和粉煤灰的交互作用较为显著。而粉煤灰和减水剂的交互作用以及砂率和减水剂的交互作用相比于砂率和粉煤灰的交互作用并不是很明显,这与方差分析中P值结果PAB=0.143 8 图3 粉煤灰与砂率的交互作用 图4 粉煤灰与减水剂的交互作用 图5 砂率与减水剂的交互作用 对响应面模型进行全局优化,得到最优工艺条件及相应的预测值并进行试验验证,结果见表9。这样基于预测结果,在试验验证时各因素水平取表中的实际条件。 表9 响应面模型预测及试验验证结果 通过以上数据处理的过程可以看出,响应面设计的试验次数比正交设计稍多,选择的代表性点也更加全面,如图2所示。其可以建立一个二元回归方程的数学模型,所以分析的数据为整个拟合曲面上的点,得到的最优因素水平也不再局限于给定水平的组合,所以准确度也相对较高。在方差分析结果中同时包含了一次项、二次项和平方项的显著性,即在试验设计前不需要考虑是否存在交互作用,借助二维等高线和三维响应曲面等直观的图像就可清晰地反映因素间交互作用的显著性,使得试验设计更加科学,结果的稳定性和准确性也更高;同时,响应面设计还可以通过多项式求解对抗折强度进行预测,即在最优条件下28 d抗折强度可以达到6.4 MPa。 (1)以路用混凝土基于目标性能的配合比优化为例,介绍了正交设计和响应面设计2种试验设计方法,两者得到的最优工艺参数接近,但正交设计是通过对9个代表性试验点进行试验设计得到给定水平范围内的最优组合参数,而响应面设计通过对12个基础点和1个中心点进行试验设计,得到的最优因素水平不再局限于给定水平的组合,准确度也有所提高,而且还能对性能进行预测。 (2)正交试验需要先确定是否存在交互作用,再合理选择正交表,其分析的是离散型数据,方差分析结果只能得到各因素的显著性;而响应面试验是对拟合曲面上的数据进行一个整体分析,在方差分析结果中同时包含了一次项、二次项和平方项的显著性,同时还能借助直观的响应面图像清晰反映因子之间的交互作用,不需要在设计前考虑交互作用是否存在,使得试验设计更加科学,结果的稳定性和准确性也更高。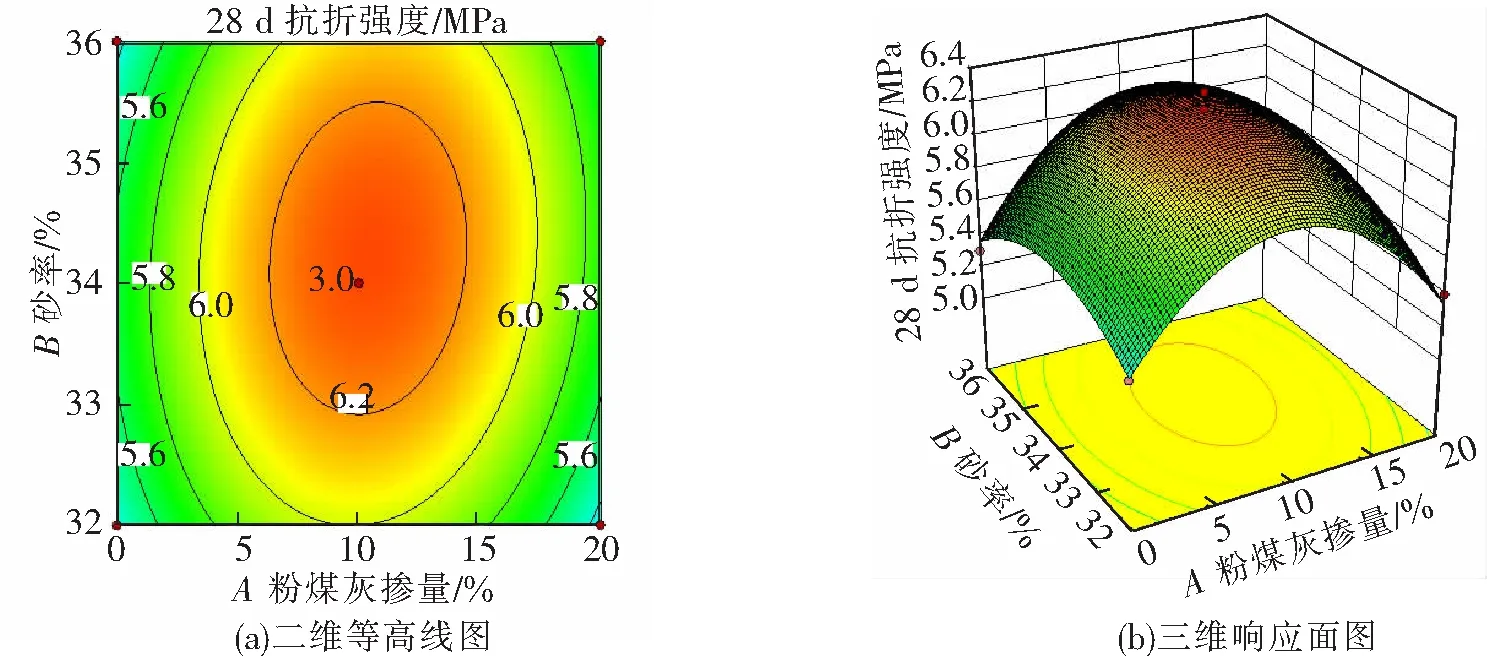

3 结论
