基于车辆模型紧耦合的封闭园区车辆定位方法*

秦晓辉，王哲文，庞 涛，史维清，孙 宁，胡满江

（汽车车身先进设计制造国家重点实验室，湖南大学机械与运载工程学院，长沙410082）

前言

近年来随着自动驾驶技术研究的不断深入，多种应用场景下的自动驾驶解决方案应运而生。诸如港口、工厂园区等相对封闭区域因车辆行驶路线固定、交互环境简单等特点，成为了自动驾驶技术商业化落地的首选场景。自动驾驶技术包含环境感知、自主定位、决策规划和运动控制等多项技术，其中自主定位技术是自动驾驶车辆实现复杂环境下自主运动的重要基础。

自主定位技术的实现主要依靠自动驾驶车辆上安装的外部传感器。惯性导航系统（inertial navigation system，INS）包括全球导航卫星系统（global navigation satellite system，GNSS）和惯性测量单元（inertial measurement unit，IMU），在开阔环境中定位精度较高，可为自动驾驶车辆提供全天候定位服务。然而GNSS定位依赖远距离在轨卫星的授时信号，一旦车辆处于无线电信号强度不稳定或信号丢失的环境中，例如道路两侧堆放大量集装箱的港口、植被或建筑物密度较高的园区等，定位精度将无法保证甚至无法进行定位。且自动驾驶车辆常用的低成本IMU只能在极短时间内保证载体定位精度，局限性较大。

对于GNSS信号存在遮挡场景中的自动驾驶车辆自主定位，国内外学者进行了大量研究。在此工况下，通常有4种位姿估计方法：基于模型的方法、基于直接传感器的方法、基于间接传感器的方法和上述3种方法的融合［1］。基于模型的方法使用车辆模型在静态和动态响应中获得定位结果，Ren等基于阿克曼原理分析车辆的运动学特征，建立考虑误差的车辆运动学模型推算车辆的转向角、航向角和转弯半径等运动状态［2］。Xiong等结合基于模型和间接传感器的方法，通过基于车辆动力学模型和间接传感器之一的IMU来完成位姿和滑移角估计［3］，但该方法中的IMU累积误差无法被很好地消除。Xia等提出一种基于IMU的运动学模型，结合用于补偿误差累积的动态模型并采用开环积分的方法来估计车辆的位姿和横向速度［4］。

随着技术的不断发展创新，摄像头和激光雷达（light detection and ranging，LiDAR）等直接传感器被广泛应用于自动驾驶车辆的定位系统中，以摄像头为传感器进行定位时通常对场景光照要求较高，在具有玻璃、白墙等特征较少的场景鲁棒性较低［5］，而且算法构建的地图点较为稀疏，在动态物体较多的场景中容易失效［6］。而LiDAR定位方法在三维纹理特征丰富的环境中具有光照不变性和较高的定位鲁棒性，适用于光照受植被或密集建筑物影响较大的封闭园区环境。直接传感器的广泛应用为自动驾驶定位问题提供了新的解决方案，融合不同类型传感器的位姿估计方法逐渐成为研究热点。融合方案大致分为两类：松耦合和紧耦合。松耦合方法融合不同传感器的数据处理结果以得到最终定位结果［7-8］。Zhang等提出的激光里程计使用IMU测量作为先验并消除点云畸变但并不对IMU数据进行优化处理，多应用于室外自动驾驶试验场景，累积误差较为明显［9］。Yang等提出了一种考虑系统初始化偏差的因子图，基于松耦合原理和扩展卡尔曼滤波器消除定位累积漂移，并重建全局一致的三维地图［10］。孙宁等提出一种基于GPS∕radar集成的多车系统定位方法，先通过GPS和radar对车辆位姿进行粗估计，再将粗估计结果通过车车通信进行融合以得到更精确的位姿估计结果［11］。曹立波等提出一种基于GPS∕视觉融合的自动驾驶定位方法，在车道判别的基础上利用超宽带通信技术进行单锚点V2I定位［12］。然而该方法仅对静态定位误差进行分析，鲁棒性较低。紧耦合方法将不同传感器测量集成后共同构建运动方程和观测方程，并进行联合优化，有助于提高定位精度［13］。一个迭代误差状态滤波器被Qin等设计用于融合LiDAR和IMU测量，算法鲁棒性较高［14］。Ye等提出了一种紧耦合3D LiDAR-IMU位姿估计算法，使用IMU进行帧间预测辅助LiDAR配准，联合优化各传感器代价函数以获得实时一致的位姿估计［15］。然而，上述两种方法均有局限性，例如在崎岖道路或植被较多的场景下，位姿的估计结果尤其是竖直方向上的平移位姿估计存在误差累积的情况。

受上述工作启发，本文中提出了一种基于车辆模型紧耦合的封闭园区车辆定位方法，该定位方法可良好适应GNSS信号受遮挡的封闭园区场景，且不受园区中因货物运输等因素造成的环境变化影响，具有实时性和鲁棒性。在充分利用LiDAR和IMU测量的基础上辅以车辆运动学模型约束车辆位姿优化方向，采用模块化设计思路对系统分3个模块进行建模，并使用紧耦合方法进行联合优化以获得高一致性的自动驾驶车辆位姿估计。本文主要贡献如下：

（1）提出一种基于车辆模型紧耦合的LiDARIMU融合定位方法，实现了自动驾驶车辆在弱GNSS信号环境下高精度的鲁棒定位；

（2）利用IMU测量和系统状态量为LiDAR帧间配准提供先验信息，并采用基于局部地图的方法以提高配准精度；

（3）利用系统状态信息构建车辆运动学模型以充分利用车辆运动信息约束位姿优化方向，并预测自动驾驶车辆的6自由度位姿；

（4）通过不同弱GNSS信号场景的实车试验对该方法进行验证，其性能优于室外定位导航应用较为广泛的A-LOAM定位方法和仅使用LiDAR-IMU紧耦合的定位方法。

1 系统架构

本文中提出的基于车辆模型紧耦合的封闭园区车辆定位方法系统架构如图1所示。主要包括4个部分：LiDAR里程计、IMU里程计、车辆运动学模型预测方程和联合优化。

图1 考虑车辆运动学模型约束的紧耦合车辆定位方法系统架构

LiDAR测量值，即点云，通常会由于自动驾驶车辆的运动而产生畸变，常用状态估计的方法进行纠偏。状态估计指充分利用IMU测量值、优化后的系统状态量和IMU坐标系与LiDAR坐标系之间的外部参数来估计自动驾驶车辆的实时状态。对纠偏后的点云进行滤波以剔除异常值，并从点云中提取特征点，包括边缘点和平面点，用于配准。随后可构造基于LiDAR测量的重投影残差。

IMU测量可为LiDAR里程计提供较准确的初始值且可为点云纠偏提供状态估计量，包括来自加速度计的加速度和陀螺仪的角速度，会受到零偏和噪声的影响，在IMU里程计残差构建和初始化过程中，需要考虑这些因素对自动驾驶车辆位姿估计造成的偏差。

车辆运动学模型的输入来自先前LiDAR测量时刻的联合优化结果，包括平移、速度和旋转。本文在自行车模型的基础上，设计了一种改进的运动学模型，利用3自由度输入对自动驾驶车辆的6自由度位姿进行预测，并对LiDAR测量时刻的位姿进行预测。最后利用预测量约束车辆位姿，得到基于车辆运动学模型预测的残差。

以上3部分残差以紧耦合方式被综合起来形成代价函数，以车辆当前位姿为待优化变量，使用Ceres求解，得到车辆当前位姿的最优解。

2 紧耦合定位方法

本节介绍LiDAR、IMU里程计的残差构建，改进的车辆运动学模型构建方式和预测分析，以及紧耦合定位方法代价函数的推导过程。

2.1 系统状态量构建

系统采用图2所示帧间匹配方式，以LiDAR测量时刻为时间基准，以IMU坐标系为测量基准融合LiDAR帧间传感器测量值和车辆模型预测值构建局部地图。对于车辆运动学模型更新模块，其输入量来自当前LiDAR帧时刻和前两个LiDAR帧时刻的系统状态量，通过阿克曼转向原理和车辆运动方程构建车辆运动学模型并预测下一时刻自动驾驶车辆运动状态。对于IMU测量更新模块，高频IMU测量通过线性插值和预积分得到相邻LiDAR测量时刻的IMU预积分量以构建约束。对于LiDAR测量更新模块，定义局部地图LiDAR关键帧，目的是通过将关键帧后的普通LiDAR帧投影到关键帧并利用特征点配准方法构建稳定性较强的约束。相邻LiDAR测量时刻间的状态量定义如下：

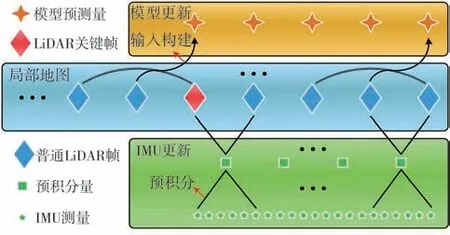
图2 系统中不同数据的帧间匹配方式

式中：w表示世界坐标系，重力的方向与世界坐标系的竖直方向对齐；b表示IMU坐标系；i表示LiDAR测量时刻；X为系统状态量，且均以IMU坐标系为参考；Xbk为k（k∈[0，i]）时刻IMU状态量，包括相对于世界坐标系的平移、速度和旋转，分别以p、v和四元数q表示；ba和bg分别为加速度计和陀螺仪的零偏。

2.2 LiDAR测量残差

经IMU测量值和优化后的系统状态量纠偏后的点云L被用来构造LiDAR测量残差。首先用体素网格滤波器对点云进行降采样以提高点云质量。然后提取点云特征点，并构造特征线和特征面，同时根据曲率大小将特征点分为边缘点和平面点。之后根据点云中边缘点和平面点到特征线和特征面的距离构造LiDAR测量残差。

对于点云帧中的边缘点，在前一帧点云中提取其对应点，并利用KD树搜索与该点距离最近的两点以构建特征线，同时计算该点与特征线间的距离以构建LiDAR测量的一部分残差。对于点云帧中的平面点，与上述方式类似，在前一帧点云中提取其对应点并利用KD树搜索与该点距离最近的3点以构建特征面，同时计算该点与特征面间的距离以构建LiDAR测量的另一部分残差。综上，LiDAR测量残差可表示为

式中：l表示LiDAR坐标系；e和s分别表示边缘点和平面点；和分别表示由边缘点和平面点构造的LiDAR残差；R为旋转矩阵，虽然四元数主要在状态量的表示中被使用，但旋转矩阵也用于简化旋转和偏导数等的计算；m为特征线的方向向量和为Li+1到Li的转换；n为特征面法向量；D为特征面一般方程中的常数项。

2.3 IMU预积分和残差构建

本文在Shen等的工作基础上［16］，参考Forster等的方法［17］，考虑了IMU零偏和噪声对自动驾驶车辆位姿估计造成的偏差。

对于原始IMU测量，采用线性插值使其时间戳与LiDAR时间戳对齐。随后对测量值进行积分，对上一IMU测量时刻的IMU测量值进行积分可得到当前IMU测量时刻的平移、速度和旋转，结合IMU坐标系与世界坐标系间的旋转变换可将相对于世界坐标系的积分量转换为相对于IMU测量时刻的积分量，即为预积分量。预积分量只与IMU测量值相关，表示一段时间内的IMU测量，它的引入使得IMU坐标系相对于世界坐标系的旋转优化更新后不需要对IMU测量重新进行积分，大大减少了运算量，提高了系统运行效率。预积分量被用作测量值对状态量进行约束并构建IMU测量残差：

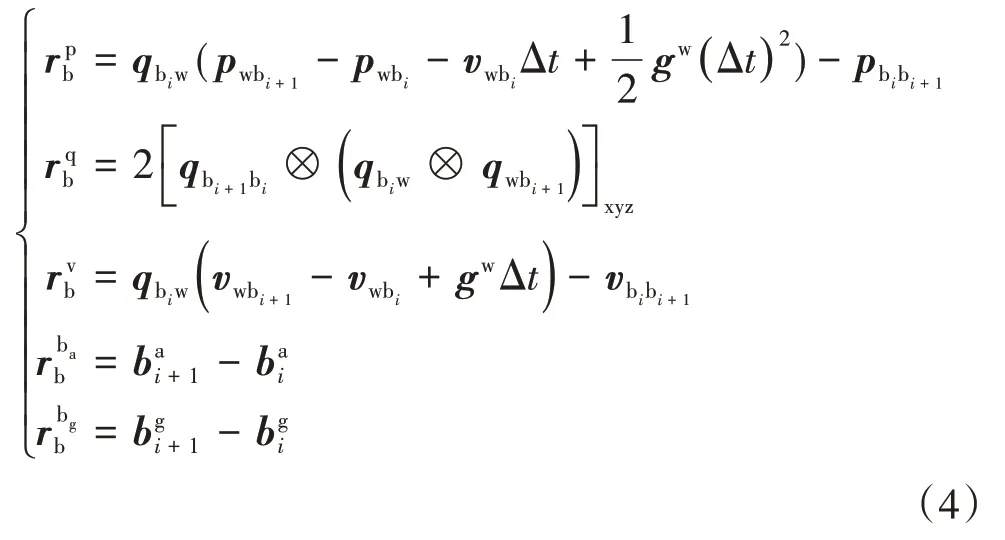
式中：pbibi+1、qbi+1bi、vbibi+1分别为平移、旋转和速度在相邻LiDAR帧间的预积分量；gw为世界坐标系下的重力加速度；[·]xyz为取四元数虚部的运算；⊗表示四元数的乘法运算。

2.4 车辆运动学模型测量残差

基于车辆运动学模型的位姿预测方法充分利用之前LiDAR测量时刻的状态量（包括平移、速度和旋转）来估计自动驾驶车辆的6自由度位姿，不添加额外传感器以避免由于新增传感器而导致的额外误差。同时提出平面假设，即相邻两LiDAR测量时刻间车辆在同一平面上运动。根据阿克曼转向原理和运动学方程等预测相邻LiDAR测量时刻间自动驾驶车辆的位姿变化。

改进的车辆运动学模型可利用二维车辆状态信息对车辆相对于世界坐标系的三维位姿进行预测，具体建模方法如图3所示，图中车辆坐标系以车辆后轴为中心，该图基于自行车模型原理对3个相邻LiDAR测量时刻的车辆参数进行描述。图中XwOwYw为世界坐标系，XkvOkY kv为k时刻（k=i-1、i、i+1）以自动驾驶车辆后轴中心为原点的车辆坐标系。OkMk表示k时刻自动驾驶车辆所在位置，此时刻前轮转角为δk，相对于前一时刻车辆的横摆角变化量为ψk。自动驾驶车辆轴距为L，速度vk方向始终与车头朝向平行，即沿Xkv方向。根据阿克曼转向原理，假设自动驾驶车辆在两相邻LiDAR测量时刻间以相同半径R作圆周运动，点C为轨迹的圆心。R可通过相邻LiDAR测量时刻自动驾驶车辆在世界坐标系中的位置坐标和空间中圆的一般方程来计算。基于图中的几何关系，可得i和i+1时刻的前轮转角：

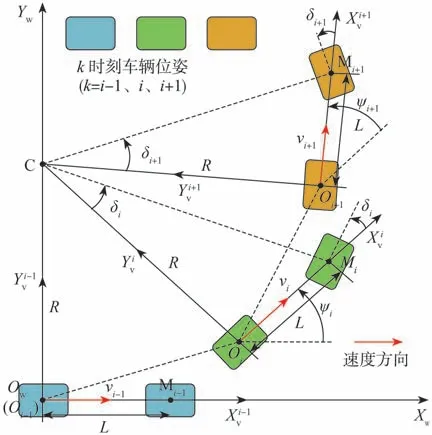
图3 改进的车辆运动学模型原理图

式中：L为车辆轴距；R为转向半径。

对于i时刻速度状态量vwbi，将其转换到车辆坐标系并提取沿X轴的速度分量：

式中：qvb为IMU坐标系到车辆坐标系的旋转外参；R11为提取沿X轴方向速度的变换矩阵。

综上所述，构造自动驾驶车辆相对于上一LiDAR测量时刻的位姿增量预测方程：

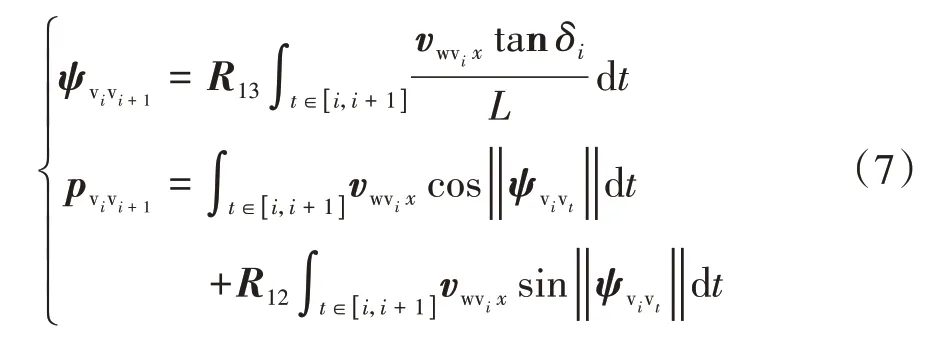
式中：ψvivt和pvivt为t时刻自动驾驶车辆相对于i时刻车辆坐标系的横摆角和平移增量；R12为提取沿Y轴方向速度的变换矩阵；R13为提取绕竖直方向旋转的变换矩阵。

对于横摆角增量ψvivt，采用罗德里格斯公式并结合自动驾驶车辆运动平面的法向量nv计算相邻LiDAR测量时刻间的旋转矩阵：

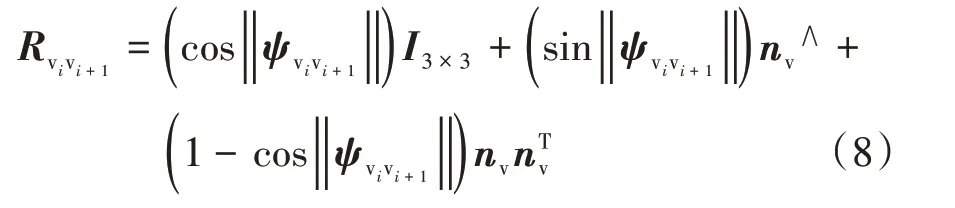
式中：I3×3为3阶单位矩阵；⋀为反对称符号。

从而可得与旋转矩阵Rvivi+1相对应的四元数qvivi+1，结合i和i+1时刻的旋转状态量qwbi和qwbi+1及IMU坐标系与车辆坐标系的旋转外参qbv可得车辆运动学模型旋转预测残差：

式中*为四元数的共轭运算。

对于平移增量pvivi+1，转换到世界坐标系：

式中：Rwbi为旋转状态量qwbi对应的旋转向量；pwbi为平移状态量；Rbv和pbv为IMU坐标系和车辆坐标系的旋转和平移外参。

从而可得车辆运动学模型平移预测残差为

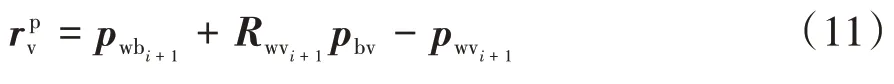
式中Rwvi+1为i+1时刻世界坐标系下的旋转。

综上可得车辆运动学模型残差为

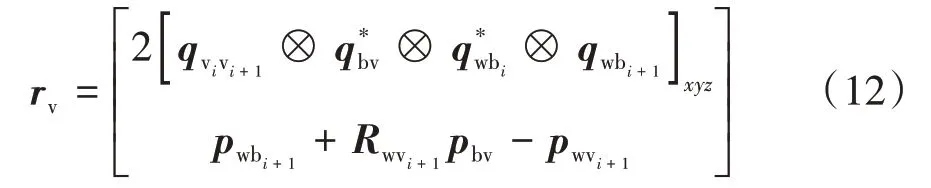
2.5 系统优化求解

对于由LiDAR、IMU和车辆运动学模型得到的位姿估计残差，采用紧耦合方法进行联合优化。通过最小化所有残差的先验和马氏范数之和获得最大后验估计：

3 试验与分析

为评估本文中提出的基于车辆模型紧耦合的封闭园区车辆定位方法，在不同封闭园区场景进行了试验，并与室外定位导航应用较为广泛的A-LOAM定位方法进行对比。A-LOAM定位方法结合高频定位和低频建图两个线程实现三维位姿估计，其以低漂移、低计算量和较高精度等特点成为激光SLAM中的主流方法之一［18］。由林肯MKZ轿车改装的自动驾驶平台进行相关试验，该平台配备了VelodyneVLP-32C LiDAR和北斗星通npos220惯性导航系统（包括GNSS和IMU），如图4所示。所有试验定位方法均在配备Intel i5 CPU、2.3GHz四核、16GB RAM和Linux系统的计算机上运行。在自动驾驶车辆行驶时实时采集LiDAR、IMU和GNSS数据，其中GNSS数据作为真实值以评估定位方法精度。

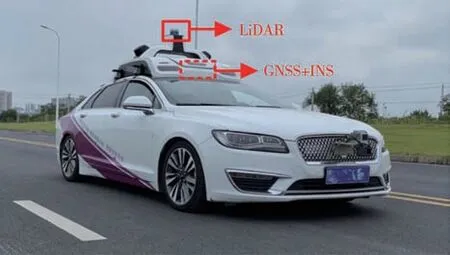
图4 自动驾驶试验平台车

图5所示为封闭园区试验场景的点云地图和试验车行驶轨迹，其中场景a的轨迹长度为965.065 m，场景b的轨迹长度为903.528 m。轨迹起点和终点以及试验车行驶方向均在图中标示。在以上两个场景对A-LOAM、本文提出的基于多传感器紧耦合的LiDAR-IMU定位方法和基于车辆模型紧耦合的LiDAR-IMU-VM（Vehicle Model）定位方法分别进行试验，并对试验结果的相对误差、绝对误差和竖直方向误差进行对比。

图5 两个不同封闭园区试验场景的点云地图和自动驾驶车辆行驶轨迹

表1为3种定位方法的相对定位误差对比。其中：A-LOAM在两个试验场景中的平移与旋转精度均较差，本文中提出的LiDAR-IMU定位方法相对于A-LOAM在两个试验场景中的平移与旋转误差均有较大幅度下降，加上车辆运动学模型的LiDARIMU-VM定位方法的平移与旋转精度表现最好，在试验场景b中的平移与旋转误差分别降至0.514 8%和0.004 0（°）∕m，在试验场景a中效果更好，只有0.372 0%和0.002 1（°）∕m。

表1 不同定位方法在不同场景的相对定位误差

图6所示为3种定位方法在两个不同场景的绝对定位误差对比。图中所示在两个不同试验场景中LiDAR-IMU-VM定位方法的绝对误差均值均为最小，分别为1.412 6和1.223 9 m，对于A-LOAM的绝对误差均 值2.760 9和2.437 9 m及LiDAR-IMU定位方法的绝对误差均值2.072 4和1.866 8 m，定位精度有较大幅度提升。特别的，在场景a下，ALOAM算法在试验终断的误差累积虽然有所收敛，但其绝对误差仍较大，超过了4 m，LiDAR-IMU定位方法的误差累积有所减小，LiDAR-IMU-VM定位方法的误差累积最小，且终段收敛明显。在场景b下，A-LOAM的误差持续累积并逐渐发散，LiDAR-IMU定位方法误差在试验终段存在收敛趋势，而LiDARIMU-VM定位方法在试验前中段相对另外两种方法表现较好，且误差累积较小，试验终段误差虽有增加趋势，但仍可收敛到较低水平。

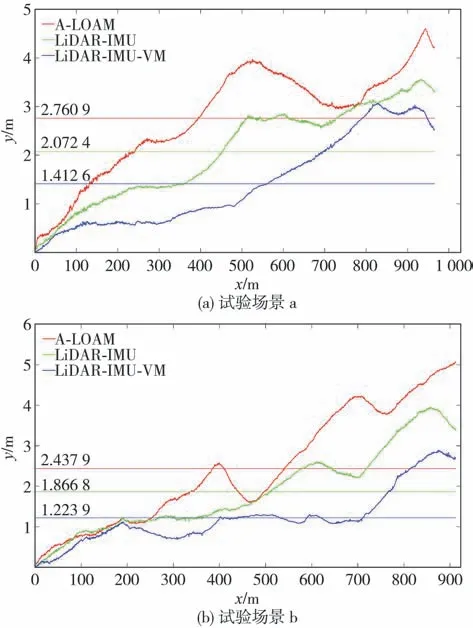
图6 3种定位方法在试验场景a、b下的绝对定位误差

图7所示为竖直方向上3种定位方法的平移位姿估计与Ground Truth平移位姿间差值的绝对值对比。在试验场景a下，A-LOAM的竖直方向误差绝对值最大达到5.075 9 m，误差均值为2.222 5 m。LiDAR-IMU定位方法的最大绝对误差值降至2.382 4 m，误差均值降至1.245 1 m，相较于ALOAM有较大提升，而LiDAR-IMU-VM定位方法的最大竖直方向误差则降至1.493 1 m且误差均值仅为0.443 1 m。在试验场景b下，3种定位方法的误差绝对值均值分别为3.076 6、2.237 2和0.400 6 m。且LiDAR-IMU-VM定位方法将最大竖直方向误差控制在1.524 1 m以内，相较于A-LOAM和LiDARIMU定位方法的最大竖直方向误差5.871 5和8.255 0 m，优势明显。

图7 试验场景a、b下竖直方向3种定位方法位姿估计结果与真实位姿间差值的绝对值对比

表2为本文LiDAR-IMU-VM定位方法的分模块耗时对比，其中场景a和场景b下的激光里程计耗时分别为68.402 3和56.823 1 ms。IMU模型位姿估计模块和车辆运动学模型位姿预测模块由于在优化基础上进行构建，其耗时相对较少，仅为0.044 2和0.040 1 ms。而建图模块的耗时最多，在场景a和场景b下分别为278.332 4和256.250 4 ms。由于场景a的试验里程较场景b长60余米，故场景a下的算法总耗时346.778 9 ms略高于场景b下的算法总耗时313.113 6 ms。综上，本文提出的LiDAR-IMUVM定位方法在两封闭园区场景下的算法耗时均可满足自动驾驶车辆定位的实时性要求。

表2 不同定位方法在不同场景的定位耗时对比

从上述试验中可以看出，本文中提出的基于车辆模型紧耦合的封闭园区自动驾驶定位方法在相对定位误差、绝对定位误差和竖直方向误差这3个定位精度评价标准下，相较于A-LOAM和单纯的LiDAR-IMU定位方法均表现更好，且具有较好的实时性、稳定性和鲁棒性。为GNSS信号差或无GNSS信号的封闭园区自动驾驶定位解决方案提供了可靠的新思路。

4 结论

本文中提出了基于车辆模型紧耦合的封闭园区车辆定位方法，其借助改进的车辆运动学模型，可在封闭园区环境中为自动驾驶车辆提供一致性较高的定位结果。该定位方法引入了车辆运动学预测模块以提高定位精度，但未使用除LiDAR和IMU以外的传感器。试验结果表明，在建筑物密度较高的封闭园区环境中，所提出的定位方法的定位精度和鲁棒性较高。

未来将改进点云的特征提取方式，并增加回环检测模块，以在该自动驾驶车辆定位方法的基础上提高其在园区复杂场景例如树木较多的道路、特征较少的弯道和连续上下坡道路等定位可靠性的同时改善定位误差累积现象。