基于表面温度和增量容量的锂电池健康状态估计*
2021-09-30林名强吴登高郑耿峰
林名强,吴登高,郑耿峰,武 骥
(1.福州大学电气工程与自动化学院,福州350108;2.中国科学院海西研究院泉州装备制造研究所,晋江362216;3.福建省特种设备检验研究院,福州350008;4.合肥工业大学汽车与交通工程学院,合肥230009;5.安徽省智能汽车工程实验室,合肥230009)
前言
近年来,新能源汽车迎来高速发展时期,其安全问题成为行业内外关注的焦点[1]。随着锂离子电池技术的蓬勃发展,使其在电池储能系统和新能源汽车领域得到广泛的使用,发挥着重要的作用。然而,使用次数的增加将会不可避免地缩短电池寿命,过充过放和不当的使用则会加速电池老化,引发潜在的系统故障和安全问题,因此,对电池健康状态的精确监测成为确保汽车安全可靠运行的重要因素[2]。容量和内阻是直观描述和评价电池老化程度的两个最常用的指标[3],其中容量指标更直观地反映了电池当前的老化状态,健康状态通常表示为当前容量与初始容量的比值。IEEE标准1188—1996中指出,当电池当前容量降低到初始容量80%,或者当前欧姆内阻大于初始值2倍时,应该更换电池[4]。
SOH无法直接测量,通常间接利用电池内部参数如电压、内阻等与之建立映射关系从而进行估算,目前国内外对锂离子电池SOH的研究可以分为基于模型和基于数据驱动的方法。基于模型的方法主要根据电池的电化学反应,建立经验模型,通过最小二乘法、卡尔曼滤波(KF)等方法辨识参数已实现容量的估计。例如,Yu等[5]利用递归最小二乘法(RLS)对Thevenin等效电路模型进行参数辨识估计电池容量。Zheng等[6]提出了基于电化学模型的三元比例积分(PI)观测器估算容量,结合移动窗口安培计数法和迭代逼近法,提高了估计精度。刘轶鑫等[7]通过分析SOC-OCV曲线衍变规律,从中提取特征参数并采用多项式拟合方法估计SOH;基于模型的SOH估计方法虽然精度较高,但非常依赖于模型的选择和精度,而且动态准确度较差限制了其进一步发展。
近年来随着计算机技术的发展,基于数据驱动的SOH估计方法得到广泛的研究。基于数据驱动方法利用机器学习算法来建立从特征到SOH的映射。例如,Wu等[8]采用基于微分几何的方法(DGA)从恒流充电下的终端电压曲线的数千个采样点中提取特征参数,然后应用数据处理分组法(GMDH)多项式神经网络建立电压曲线与SOH的关系估计,并验证了该方法的通用性。Yang等[9]从电池充电曲线中提取了4个健康特征,应用灰色关联法对特征与SOH的关联度进行了分析,建立高斯过程回归(GPR)模型,在NASA数据集上验证了模型的有效性,达到了较高的估计精度。Weng等[10]通过支持向量机(SVM)结合增量容量分析(ICA)估计电池SOH,通过仿真和试验验证了该框架的适用性。
然而,现有的SOH估计方法主要针对电压特性,很少考虑电池退化过程中的温度变化。本文中对此提出了一种基于电池表面温度和增量容量的SOH估计新方法,贡献如下:
(1)基于温度和IC曲线的SOH估计,提出了一种新颖的基于温度的SOH估计方法,分析温度变化曲线,从中提取出3个几何特征作为健康因子,显示出与电池老化的高度相关性,同时,提取IC曲线的峰值作为健康因子,更全面地分析电池的老化行为,提高模型的鲁棒性;
(2)采用皮尔逊相关分析法评估所提取的健康因子与SOH的关联强度,将健康因子输入BP神经网络模型估计SOH;
(3)采用牛津数据集进行验证,该方法在牛津数据集8个电池上进行了验证,研究了电池差异对SOH估计的影响,结果表明,8个电池的平均误差均在2%以内。
1 电池老化数据分析与特征提取
1.1 牛津数据集
牛津数据集[11]可作为SOH估计方法开发、分析和验证的主要数据集,记录了8个标称容量为740 mA·h的Kokam袋式电池的老化数据,分别记为Cell 1-Cell 8。电池阴极材料由锂钴氧化物和锂镍钴氧化物组成,阳极材料为石墨。在老化试验中,8个电池在2C电流下重复充电,并使用动态工况放电,以模拟汽车实际行驶状况。每100次老化循环,进行1C电流充放电以测量电池容量。电流、电压和表面温度等由Bio-logic MPG-205电池测试仪记录,间隔1 s。8个电池的容量变化如图1所示。

图1 牛津数据集8个电池容量衰退曲线
1.2 温度变化曲线获取
由于温度传感器精度有限,如果直接计算容易受到外界噪声的影响,产生较大偏差,所以为了避免这类问题,参照文献[12],本文中采用有限差分方法近似求取温度变化率,计算公式为

式中:T为温度;L为采样间隔。若L取较大值则反映较大区间的整体温度变化,所以会降低噪声的影响,但另一方面则会导致无法捕捉细微的温度变化。相反的,若L取较小值则会受到噪声影响,产生误差。本文中根据温度记录点数量取采样间隔L=40,并进一步对曲线采用高斯过程平滑以降低噪声的影响。
图2为Cell 1的部分DT曲线。可以看出:电池温度变化率首先经历先减小后增大的过程;之后温度变化最为剧烈,且随着锂电池SOH的降低表现出不同的行为。例如,随着锂电池SOH的降低,温度变化率在左侧的峰值P1逐渐降低,而在中间的谷值P2则整体逐渐增大,并且二者之间的电压差ΔP呈现逐渐缩小的趋势。随后温度变化率在经历逐渐上升到峰值后总体呈现降低的趋势,但不同SOH间的曲线变化不明显。综上所述,中间部分随着SOH的减小,DT曲线呈现出明显的单调变化趋势,有助于老化机理的研究和SOH的估计。因此,本文选取曲线左侧的峰值P1、中间的谷值P2以及二者间的电压差ΔP作为反映锂电池SOH变化的3个健康因子。
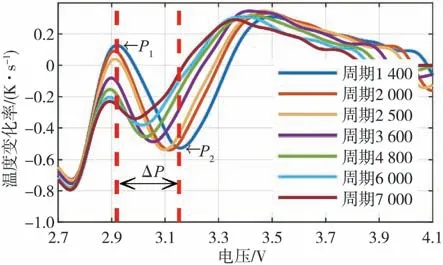
图2 Cell 1部分DT曲线
1.3 IC曲线获取
IC分析最初来源于汤普森[13]在1979年对材料科学领域方面的研究。后来在20世纪90年代,Dahn使用它来研究锂电池中的碳材料[14]。近几年,许多学者也开始应用此方法研究锂电池的容量退化机制。数学上,IC表示为在一个连续的电压增量上所增加的电池电量,在恒流充电模式下,IC计算公式为

式中:Q为容量;U为电压;t为采样时间。与标准电池老化测量(例如内阻和容量衰减评估)方法不同,IC分析从电极水平方面研究电池的老化机制,其显著优点之一是能将电池电压平台分别转化为IC曲线上清晰可识别的峰值,描述了锂离子活性材料插层和脱层过程中电池的相变特性。另一个关键点是IC分析能够在线实现,由于这些优点,IC分析被认为是研究电池老化机制的关键技术之一,具有巨大潜力。以牛津数据集中的Cell 1为例,图3说明了电池寿命演变过程中IC曲线的变化。随着循环次数的增加,IC曲线变得平缓,曲线峰值即PICC逐渐降低,且趋势明显。IC曲线中的峰具有独特的形状、高度和位置,它反映了锂电池充放电过程中的电化学反应[15]。根据文献[16–17],充电数据中显示的PICC降低可能与锂电池中活性材料的损失有关。随着循环次数的增加,活性物质无法再嵌入锂当中,这些内部变化对PICC有重大影响。

图3 不同周期下Cell 1的IC曲线
因此,PICC是一个描述电池容量退化的有效特征。图4显示了牛津电池数据集中8个电池在循环周期变化下的PICC曲线,随着电池循环周期的增加,PICC逐渐降低,反映出与SOH一定程度的相关性。

图4 PICC曲线
至此,4个反映锂电池SOH变化的健康特征已被初步提取,为了确定电池SOH与健康特征之间可能的相关性,采用皮尔逊相关分析法评估两个变量之间的相关程度[18],公式定义如下:

式中:n为样本数量;xi、yi分别为所选取特征与锂电池SOH;为样本均值。相关分析的结果如表1所示。一般来说,当|r|>0.8时表示两者之间具有强相关性,当|r|<0.5时则具有弱相关性。从表中可以看出所选特征与SOH具有较强相关性。

表1 不同特征与电池SOH的相关性分析
2 BP神经网络原理
BP神经网络是一种误差逆向传播训练的多层前馈网络,作为目前应用最广泛、最成功的神经网络模型之一,信号前向传播而误差反向传播是其主要特点。BP神经网络能学习和储存大量的输入-输出映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input layer)、隐藏层(hidden layer)和输出层(output layer)[20],如图5所示。

图5 3层BP神经网络结构
图中,xi为输入值,wi为权值,bi为阈值,f、g为激活函数,ai为中间值,yi为输出值。一般来说,层数越多,神经网络的误差也就越小,但是会使整个网络复杂化,增加网络的训练时间,也有可能出现“过拟合”的情况。所以1~2层隐藏层就能解决大多数问题。而隐藏层节点数目可由如下经验公式来确定:

式中:h为隐藏层节点数目;m为输入层节点数目;n为输出层节点数目;a为1~10之间的常数。数据前向传播过程中输入层到隐藏层第i个数值计算公式为

隐藏层到输出层第i个数值计算公式为

反向传播时误差通过输出层,按误差梯度下降的方式修正各层权值,向隐藏层、输入层逐层传播。信息正向传播和误差反向传播周而复始地进行,而各层权值也随之不断调整,即神经网络不断学习训练,当网络输出的误差减少到可以接受的程度,或者预先设定的学习次数时训练结束。
3 网络训练与结果分析
3.1 网络训练
本文中通过建立BP神经网络,以温度变化曲线中的几何特征和PICC为输入数据,以电池SOH为输出数据。采用交叉验证法对所建立的神经网络进行训练,每个电池的数据依次作为测试集,其余7个电池的数据作为训练集来验证方法的有效性。搭建的网络有一层隐藏层,节点数量为9,激活函数为logsig函数,其公式为

式中x为输入值。logsig函数的作用是将任意输入值转化为区间(0,1)上的输出。输出层的激活函数为purelin函数,它是一种线性传递函数,用于表达网络输入输出的线性关系。网络的训练函数为trainlm函数,采用Levenberg-Marquardt算法,由于其避免了直接计算赫赛矩阵,从而减少了训练中的计算量,对于中等规模的BP神经网络有最快的收敛速度。评估网络精度所采用的损失函数使用均方误差(mean squared error,MSE),计算公式为

式中:N为样本数量;yi为实际输出为估计输出。
3.2 SOH估计结果分析
根据提出的神经网络模型,利用8个电池数据集验证了该方法的准确性和有效性,通过与传统的基于IC特征和基于本文中提出的温度特征的神经网络进行对比进一步验证了该方法的优越性。其中,基于IC特征的神经网络模型以PICC及该点两侧0.03 V处的数据点为输入,如图3所示。神经网络模型SOH估计结果如图6所示。从图中可以看出,基于联合特征估计的电池SOH曲线与真实SOH轨迹具有高度的一致性和平滑性,而基于IC特征或温度特征的估计曲线则呈现不同程度的波动,且鲁棒性较差,如图7中Cell 2的估计误差曲线所示,第6 800周期的电池SOH出现了不明原因的骤降,此时基于IC特征或温度特征的估计模型误差分别为11.35%和9.38%,而基于联合特征的模型误差为5.95%,体现较好的鲁棒性。值得注意的是,尽管Cell 4、Cell 5和Cell 6的充放电周期数据较少,但是基于联合特征的方法依然能够在整个电池寿命期间估计SOH,最大误差小于2.5%。结合图7的估计误差曲线和表2可以进一步体现出模型的有效性。表2显示了神经网络SOH估计误差的平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)。其中,MAE用于测量SOH估计中误差的平均大小,而不考虑它们的方向;MAPE以百分比表示,是用于评估估计准确性的统计度量;描述SOH估计误差离散度和收敛性能的RMSE用于反映真实SOH和估计SOH之间的接近度。这3个评价标准可以对神经网络的SOH估算误差进行综合评价。当基于温度特征与基于IC特征的方法显示出较大差异时,联合特征估计结果能快速收敛到较小的误差并且具有较高的精度。这一现象表明,结合本文中提出的DT方法,有希望提高广泛应用的基于IC方法的SOH估计精度。除了提高估计精度外,该方法还可以提高估计的鲁棒性。由于两种方法依赖于不同的信号,如果基于IC的SOH估计器遇到传感器故障等意外干扰,基于DT的估计器仍然可以提供辅助SOH估计,反之亦然。通过这种组合,可以减少组合结果中一种方法的误差影响。这可以保证电池管理系统的基本性能,SOH估计结果之间的巨大差异可以作为故障诊断的标准。值得注意的是,Cell 2在充放电循环过程中经历了两次容量骤降的情况,此时网络的估计精度则损失较大,分别为2.55%和5.95%。可能的原因是电池在充放电循环过程中由于操作条件,例如,环境温度、充电和放电电压、机械应力等的变化或内部电池故障。

表2 神经网络估计误差
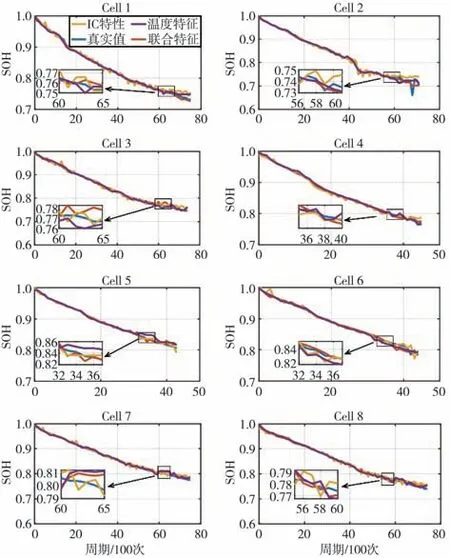
图6 神经网络估计结果
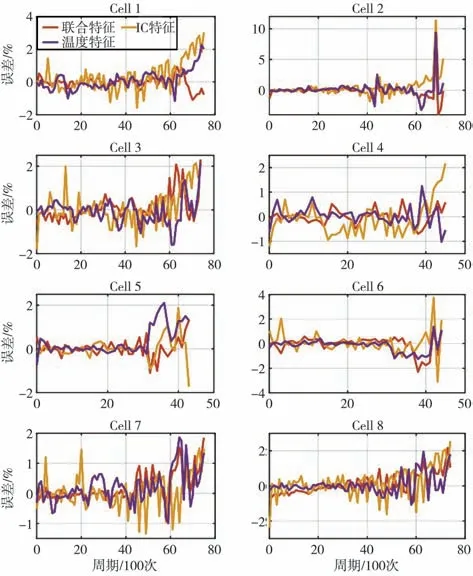
图7 神经网络估计误差
4 结论
本文中提出了一种基于电池表面温度和增量容量(IC)的SOH估计方法,分析了恒流充电过程中的温度变化曲线,从温度变化曲线中提取了3个几何特征作为健康因子,发现与电池SOH变化有很强的相关性,通过与增量容量曲线的峰值(PICC)结合作为BP神经网络的输入来建立模型估算SOH。以牛津数据集8个电池数据为依托,验证了方法的有效性,对于不同容量的电池显示出了较强的鲁棒性和稳定性,大部分电池SOH平均估计误差仅为2%以内,表现良好的甚至仅为1%左右。
从温度变化曲线及IC曲线可以看出,在Cell 2中SOH骤降的两个周期所对应的健康因子并没有表现出明显异常,所以由于故障和异常引起的动态变化的周期中可能存在其他类型的健康因子反映了此时的电池状况,值得研究人员进一步研究。
