地磁数据缺失重构方法的研究

李章 李本有 严吉 程文坤 尹天杰 谭笑

DOI：10.16661/j.cnki.1672-3791.2107-5042-2523

摘  要：地磁学是以观测为基础的科学。在日常观测中，地磁观测数据会不同程度受到仪器故障、环境干扰、人为干扰等因素的影响，造成原始数据丢失。该文依据地磁相对记录数据在邻近台站间具有较高的相关性，以缺失数据台站的邻近台站作为参考台站，通过关系拟合及加权对缺失数据进行了重构取得了较好效果。最大程度地降低补齐缺数对后续的数学分析造成的影响具有重大意义。

关键词：地磁   缺数   重构   空间相关性

中图分类号：P315                            文献标识码：A          文章编号：1672-3791（2021）06（b）-0039-03

Research on Missing Reconstruction Method of Geomagnetic Data

LI Zhang1   LI Benyou1   YAN Ji2   CHENG Wenkun2   YIN Tianjie3   TAN Xiao1

（1.Huangshan Seismic Station of Anhui Province， Huangshan， Anhui Province， 245011 China; 2.Jingxian Seismic Station of Anhui Province， Jingxian， Anhui Province， 235000 China; 3.Jiashan Seismic Station of Anhui Province， Mingguang，Anhui Province， 239461  China）

Abstract： Geomagnetism is a science based on observation. In daily observation， geomagnetic observation data will be affected by instrument failure， environmental interference， human interference and other factors to varying degrees， which will result in the loss of original data. According to the geomagnetic relative recorded data， there is a high correlation between adjacent stations. The adjacent stations of missing data stations are taken as reference stations， and the missing data are reconstructed by relation fitting and weighting， and a good effect is achieved. It is of great significance to reduce the influence of complement number on subsequent mathematical analysis to the greatest extent.

Key Words： Geomagnetic; Date missing; Reconstruction; Spatial correlation

地磁基礎观测数据有着广泛的科学应用，不仅可以用来监测地球内外部电磁场环境变化，也是研究地震、地球内部地质构造的基础。但是在日常观测中，地磁观测数据会不同程度的受到仪器故障、环境干扰、人为干扰等因素的影响，造成原始数据丢失。对数据的完整性产生了严重影响，因此基于原始数据的研究分析也会产生严重偏差。所以，如何对预处理数据中缺失的数据进行重构具有重大意义。

1  背景介绍

随着科技的不断发展和改进，地磁观测数据、观测技术更加完善。然而，社会经济快速发展，不可避免的对地磁观测数据造成干扰，影响地磁观测数据质量。以该省泾县台为例，台站附近有葛洲坝-上海、昌吉-古泉等6条高压直流输电线经过，对地磁观测影响较大。对于干扰变化处理，工作量和难度都较大，处理过程中不可避免地出现数据缺失。

2  理论方法

众所周知，地磁场是重要的地球物理场之一，而且在地表局部较小区域内，地磁场变化主要受同源影响，因此观测数据具有高度相似性。对缺失数据的补偿，国内外的一些学者做了一系列的研究，如姚法章^[1]、朱兆才^[2]、顾春雷等。因此，该文基于各台站记录到的变化磁场在时间上具有较好的同步性，且相关性较强，以缺失数据台站的邻近多个台站作为参考台站，通过关系拟合及加权在对缺失数据进行重构^[3]。

3  数据处理

3.1 参考台的选择

以观测质量较好的蒙城台为中心，选取与其距离在3 700 km内的多个台站为参考，计算其地磁相对数据的相关性，通过分析可以得出，台站间的距离Δ和地磁相对数据的相关性表现为反比关系，在两台相距1 000 km以内时，相关系数C保持在0.9以上。

3.2 参考台赋权

因为各参考台站与目标台站距离，经纬度差别很大，数据相关性表现不尽相同，因此需要对各参考台站赋权，从以下几个方面进行考虑：（1）考虑参考台站与目标台站的空间相关性与其间距成反比，间距越小，相关系数越大，其变化关系可用简单线性拟合。（2）考虑各参考臺站的权重因子和其与目标台站的空间相关性成正比，相关性越高，权重越大;和其与目标台站的距离Δ成反比，距离越大，权重越小。（3）假设参考台站与目标台站的观测数据具有线性相关，即目标台站的观测数据可以利用参考台站数据进行线性拟合^[4-5]。

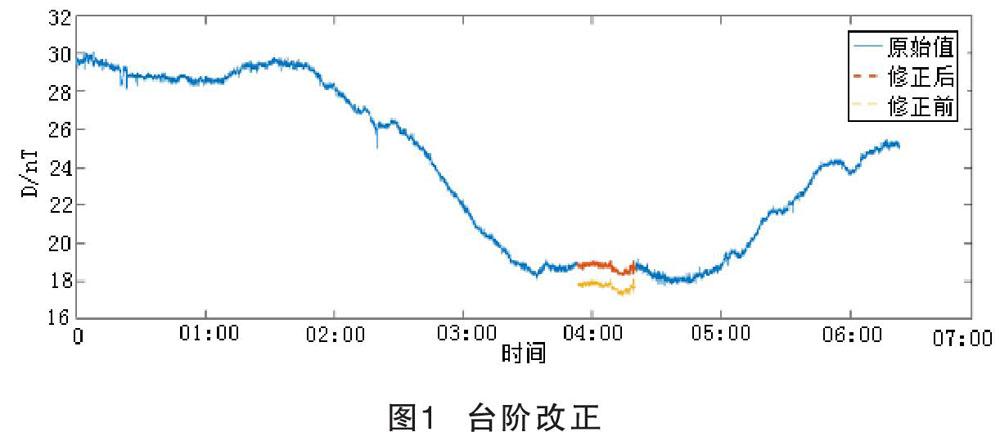
3.3 台阶改正

由上文可知参考台站与目标台站之间的经度差异，会导致观测数据的相位延时，表现在数据形态上即为重构前后有台阶差，因此为确保重构前后数据形态上连续性，对台阶差进行补偿改正，具体见图1。

4  结果检验

4.1 仿真检验

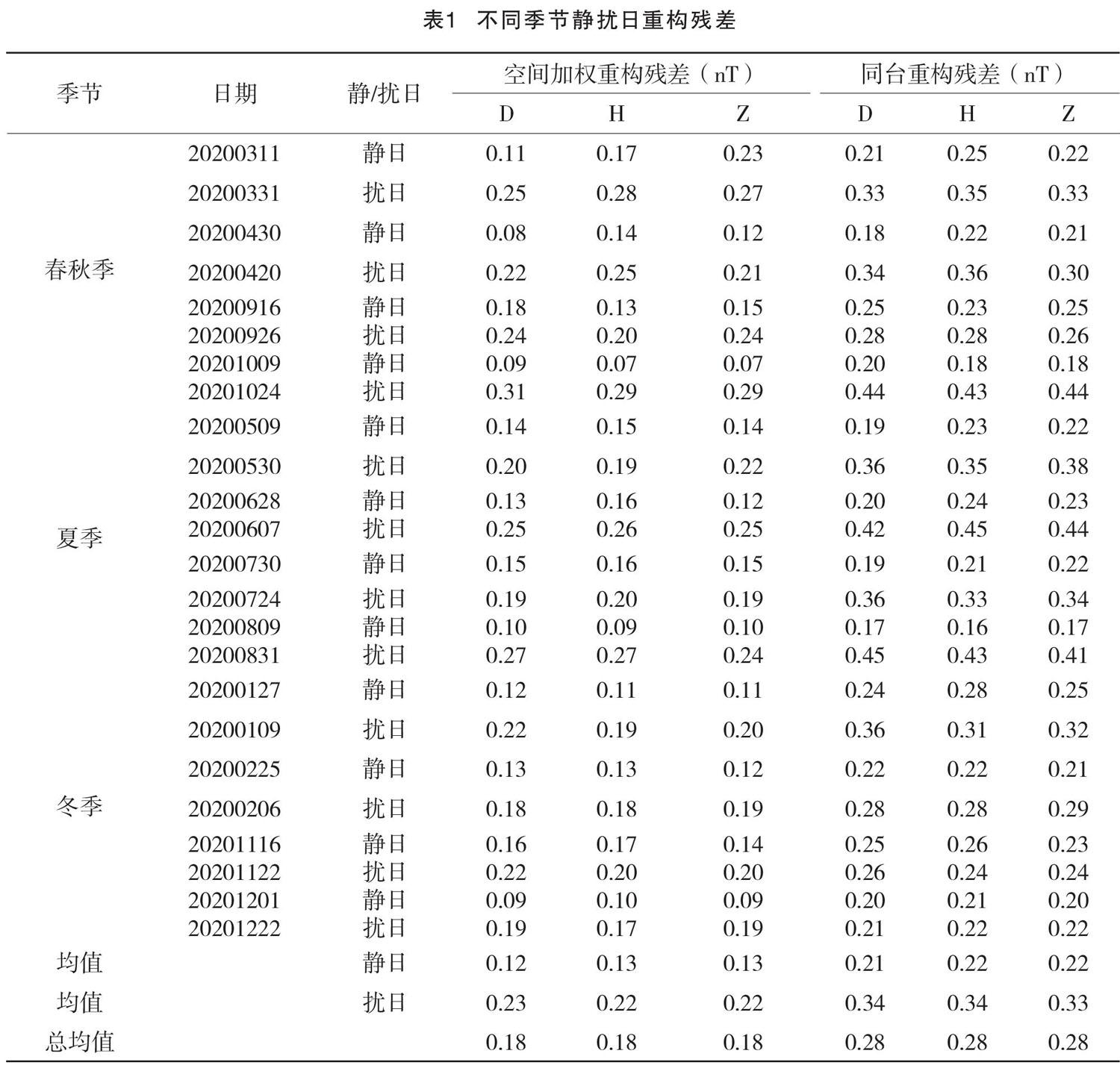
为了计算空间加权法的重构精度并检验该方法的适用性，该文进行了数据仿真。以蒙城台为目标台站，选取榆林、红山、泰安、泾县和乾陵这5个台站作为参考台站进行加权数据重构，重构结果见表1和图2。

通过表1结果可以看出，对比不同季节的磁静扰日重构残差结果可以发现，磁静日的重构残差值均要小于磁扰日重构残差值，两者平均相差约为0.11 nT。空间加权法重构残差约为0.18 nT，同台重构残差约为0.28 nT。

图2为2019年1月19日磁静日原始数据与重构数据的对比图，从图中可以发现，两条曲线几近完全重合，通过计算两者的相关系数发现，相关系数近似1，呈高度相关。重构效果很好，因此，利用空间加权法进行静日地磁数据重构是可行的^[6-7]。

4.2 功率谱

通过上面计算重构数据和原始数据的重构残差值可以看出，空间加权法重构在磁静日具有很好的效果，但为更准确验证重构效果，保证重构数据具有高精度性，通过计算分析重构数据和原始数据的Welch功率谱。通过计算后可知，重构数据和原始数据在f<0.25 Hz的低频范围内极为一致，而在f>0.25 Hz的高频噪声部分有细微差别。且低频能量高于高频能量，因此在对数据高频部分不做很高要求的前提下，重构方法是可行的^[8-9]。

5  结论

该文基于地磁相对记录在1000 km范围内有较高的相关性，利用空间加权法，以缺失数据台站的邻近台站作为参考台站，通过关系拟合及加权对缺失数据进行了重构和验证，取得了较好效果，并得出以下结论：（1）一年中不同季节，重构效果差异较大，有随季节变化而变化的特点，冬季构残差最小，春秋季次之，夏季重最大，因此重构精度易受季节影响;（2）不同地磁活动程度下的重构残差差异较大，磁静日重构残差小，磁扰日重构残差大，因此重构精度根地磁活动有很大关系;（3）空间加权法重构残差低于同台站重构残差，但该方法对相邻台站的数据质量要求较高;（4）重构数据与原始数据功率谱密度相关性较好，但是信号高频部分的重构效果较差。

参考文献

[1] 姚法章.订正法在地磁绝对观测中的应用[J].地震地磁观测与研究，1988（6）：35-38，43.

[2] 朱兆才.空间相关性分析在地磁观测研究中的应用[J].地震地磁观测与研究，1989（5）：44-49.

[3] 徐文耀.地磁学[M].北京：地震出版社，2003：45-63.

[4] 张向宇，关永贤，崔秀云.利用回归分析法补偿海底日变数据[J].物探化探计算技术，2017，39（3）：327-332.

[5] 杨学慧，杨正纲，姚休义，等.地磁观测数据中典型干扰识别与处理[J].高原地震，2020，32（3）：30-36，68.

[6] 倪晓寅.强震前短周期地磁谐波振幅比变化特征[J].地震研究，2017，40（3）：431-436，511.

[7] 袁桂平，李鸿宇，张贵霞，等.地磁垂直分量Z日变幅逐日比及其与磁暴和地震的关系[J].地震，2018，38（1）：139-146.

[8] 畅国平，王秀敏，王志敏，等.红山地震台数字地磁观测质量控制与分析[J].高原地震，2018，30（2）：46-52.

[9] 赵旭东，何宇飞，陈俊，等.基于地磁台站数据对磁暴期间环电流和场向电流的分布特征研究[J].地球物理学报，2019，62（9）：3209-3222.

作者简介：李章（1991—），男，本科，助理工程师，主要从事地震观测和前兆数据处理方面的工作。