包含密度因子的杉木可变指数削度方程研制

张森森，段爱国,2★，张建国,2，孙建军

（1.中国林业科学研究院林业研究所·国家林业和草原局林木培育重点实验室，北京100091；2.南京林业大学·南方现代林业协同创新中心，江苏 南京210037；3.中国林业科学研究院·亚热带林业实验中心，江西 分宜336600）

树干削度方程可以较好地描述树干直径随着树干高度变化的变异规律，精准估算树干商品材材积、总材积与林分蓄积，对经营管理森林，评估森林质量等具有重要实践意义和指导作用。可变指数削度方程[1-4]是通过连续函数中自变量指数的变化来更好地估计树木干形，理论上可描述任何形状的树干。可变指数削度方程已证明比简单削度方程和分段式削度方程具有更优的拟合效果及应用前景[1,4-6]。Kozak于2004年建立了一个结构简单且能高精度预估树干商品材的可变指数削度方程，并被普遍应用[7]。

除树种特性外，树干削度受年龄、立地、间伐，密度等林分经营因子以及冠长、树冠高度、枝下高等树干特征变量的明显影响，其中林分密度对树干削度的影响非常大[4,8-9]，在削度方程中加入林分密度变量可解释密度对树干干形形成的作用，而相对于其他林分变量因子，林分密度因子更容易获取。将林分密度变量构建入可变指数削度方程后，发现可提高黑云杉（Picea mariana）树干干形模拟精度，且拟合结果能解释高密度林分中林木干形削度小、低密度林分中林木干形削度大的现象[4,10]。在研究落叶松（Larix gmelinii）的削度方程时，将冠长率和密度因子构建到Max和Burkhart分段削度方程中[11]，结果表明包含冠长率和密度因子的削度方程可以提高模型的预测精度，而且密度越大，单木冠长率越小，树干的削度就越小[12]。

杉木（Cunninghamia lanceolata）是我国南方最重要的乡土针叶用材树种[13-14]，其削度方程的构建一直是研究热点问题，但仍缺乏可变指数削度方程，尤其是引入密度因子的可变指数削度方程的研制[15-16]。鉴此，以成熟龄杉木密度试验林内的树干解析资料为基础，构建了杉木可变密度可变指数削度方程，以精准预估初植密度变化条件下杉木商品材材积，为杉木林高效培育提供科学定性及定量依据。

1 材料与方法

1.1 数据来源

试验林布设于江西省分宜县大岗山年珠林场，地处罗霄山脉北端的武功山支脉，位于27°34′N，114°33′E，低山，海拔250 m，母岩为砂页岩，黄棕壤，年平均气温16.8℃，降水量1 656 mm，年蒸发量1 503 mm。采用1年生实生苗于1981年春造林，设置5种造林密度处理，每种造林密度重复3次，完全随机区组设计，同一区组坡向和坡位基本一致，林分保持自然生长状态，不进行间伐。2008年冰冻雪压造成其中4种相对高的造林密度林分中发生大量倒木（表1），对不同造林密度中的183株倒木进行了树干解析，并测量树干在0.2 m、1 m、1.3 m、2 m和2 m以上每间隔1 m处的直径，将183株倒木按密度划分，每个密度中按径阶随机分为建模数据和检验数据。不同造林密度林分的建模数据和检验数据的树高及胸径数据统计量如表1所示。

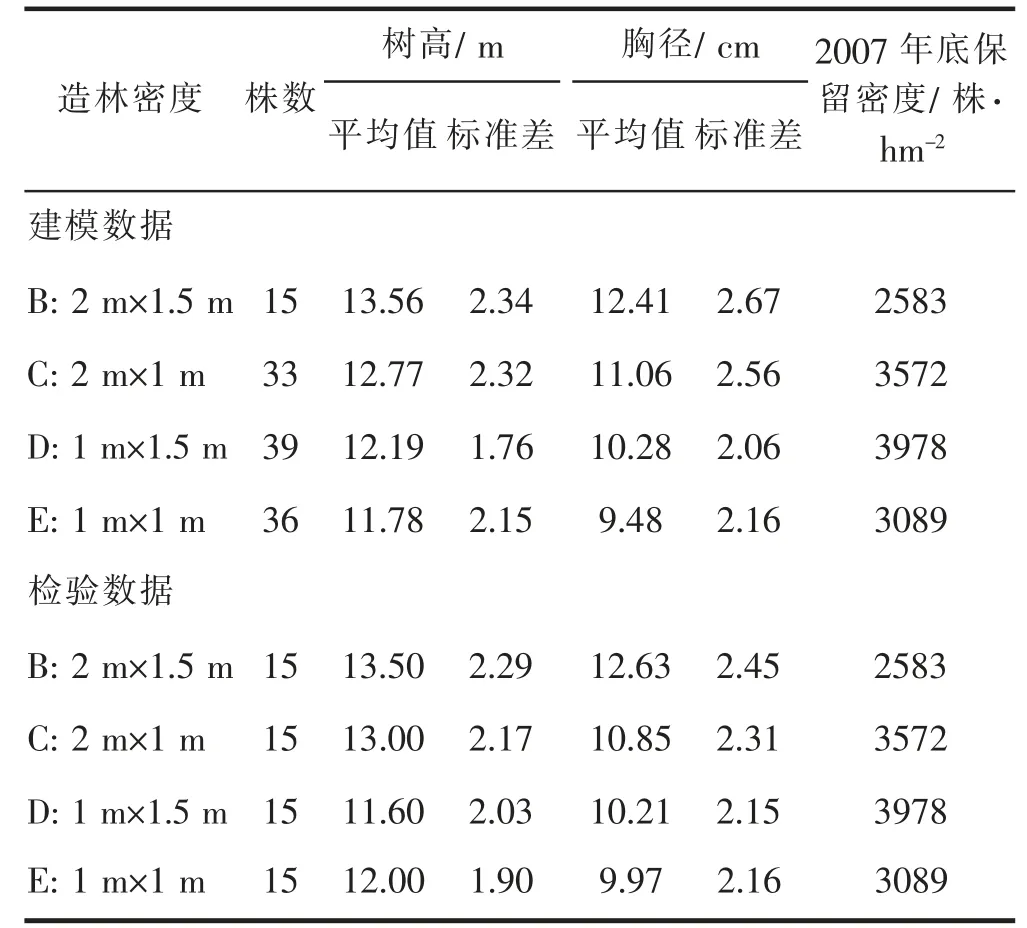
表1杉木密度试验林建模数据和检验数据概况Tab.1 Summary statistics for fit data and validation data of density test stand of Chinese fir

1.2 基础模型

选择Kozak可变指数削度方程为基础模型，模型表达式为：

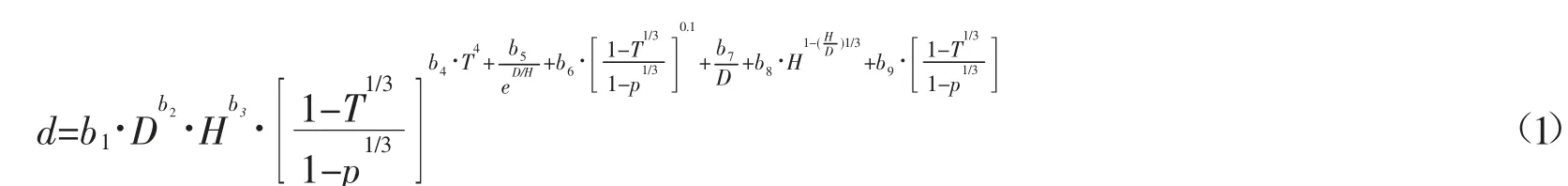
1.3 密度因子构建

在Kozak削度方程中，描述树干直径随着树高的变化而变化的部分是削度方程中的指数部分，因此密度因子可以添加在削度方程的指数部分，来反映密度因子对树干干形的影响[4]。为了检验密度因子对树干削度的影响，设置了8种密度因子形式并引入削度方程进行拟合，结果发现其中5种收敛，3种不收敛，5种 收 敛 的 表 达 形 式 为

1.4 混合效应模型建立

考虑样木效应建立混合效应模型时，由于过多的随机参数，可能会导致过度参数化或收敛的问题[17]，对选取的基础模型（1）中1～2个随机参数组合的可能性都进行拟合，通过比较统计量AIC(Akaike information criteria)、BIC(Bayesian information criteria)和-2LL的最低值来决定最优的固定参数和随机参数的组合。

1.5 评价标准

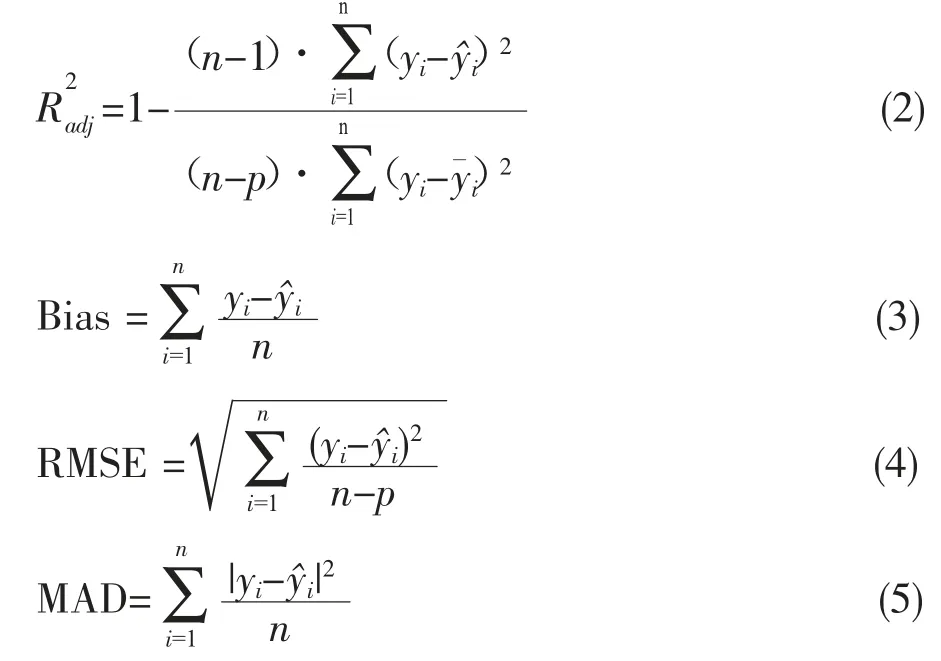
式中：yi为观测值，y^i为预测值，yˉi为观测值的平均值，n为观察值数量，p为模型参数个数。

2 结果与分析

2.1 包含密度因子的削度方程构建

表2列出了5种密度因子表达形式的参数估计和拟合统计量。发现方程1中参数b10在b10/sd和b10/sd2形式中的标准差过大，分别为25.8784和63296.2。参数的标准差过大说明参数不稳定，故而排除这两种形式。在剩下的其他3种形式中(b10/ √s d ，b10/ √3s d，b10/log(sd))，参数b10的标准差均较小，分别为0.7066、0.2510和0.3430，说明参数的数据整齐稳定，且由参数的标准误差可知，各个参数在0.05水平上显著；这3种形式的拟合统计量基本一致，R2adj、Bias、RMSE分别为0.9838、0.0040～0.0044、0.4450～0.4453，而由于b10/ √s d 相对于其他两种形式更为简洁，容易求算，故选择b10/√s d 为最优的包含密度的指数形式。引入密度因子后的Kozak可变指数削度方程表达式如下：

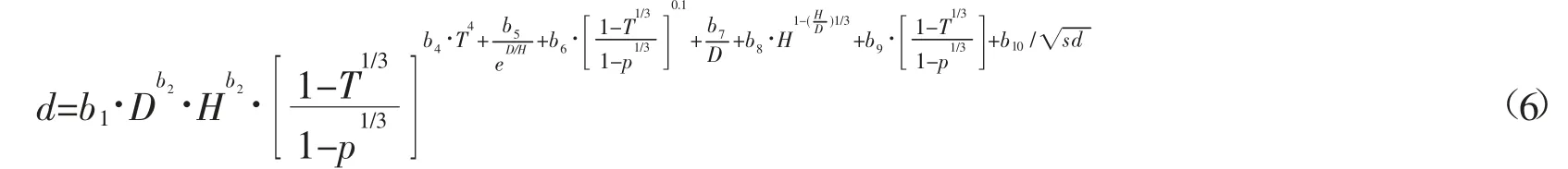
式中各参数同式1，sd为林分的初植密度(株·hm-2)，b10为估计参数。

2.2 包含密度因子的混合效应模型建立

以含有初植密度变量的削度方程为基础模型建立基于样木效应的混合效应模型，首先确定随机参数。在式6中的10个参数中选择1～2个不同随机参数的所有组合，利用S-Plus软件的nlme模块进行拟合，结果见表3。表3显示了随机参数的所有收敛组合(共44对组合)的AIC、BIC和-2LL的值，其中b6、b8随机参数组合的值最小，因此选择b6、b8为基于样木效应的混合效应模型的随机参数。

利用S-Plus软件分别对不包含密度变量和包含密度变量的Kozak削度方程用非线性回归和混合效应模型两种方法分别进行拟合，共4种不同形式，分别为不包含密度削度方程的非线性回归拟合(NLS)，包含密度削度方程的非线性回归拟合(NLSSD)，不包含密度变量削度方程的非线性混合效应拟合(NLME)，包含密度变量削度方程的非线性混合效应拟合(NLMESD)。表4显示了4种不同形式的基于样木效应的Kozak削度方程的参数估计值和拟合统计量（括号内为标准差）。其中，NLSSD模型的调整决定系数相对于NLS模型的调整决定系数提高了0.0001，NLSSD模型的平均偏差（Bias=0.0037）相对于NLS模型的平均偏差（Bias=0.0041）降低了0.0004，NLSSD模型的均方根误差（RMSE=0.4450）相对于NLS模型的均方根误差（RMSE=0.4470）降低了0.0020，NLSSD模型的平均绝对偏差（MAD=0.3359）相对于NLS模型的平均绝对偏差（MAD=0.3379）降低了0.0020。而NLMESD模型相对于NLME模型的调整决定系数（），平均偏差（Bias）和均方根误差（RMSE）都无显著变化，均分别为0.9945，0.0006，0.2603，但NLMESD模型的平均绝对偏差（MAD=0.3359）相对于NLME模型的平均绝对偏差（MAD=0.3379）降低了0.0020。可以发现，引入密度因子后，无论是非线性回归还是混合效应模型，削度方程的拟合精度均略有提高，比较而言，采用混合效应模型建立的削度方程较非线性回归模型具有更高的调整决定系数及更低的平均偏差、均方根误差和平均绝对偏差。

图1为建模数据中的不同密度林分平均木，其中包括密度为3 333株·hm-2（D=13 cm，H=13.8 m）、5 000株·hm-2（D=11 cm，H=12.7 m）、6 667株·hm-2（D=10.4 cm，H=12.2 m）和10 000株·hm-2（D=9.7cm，H=11.7 m），用包含密度因子的基于样木效应的Kozak混合效应模型拟合的模型轮廓图。发现不同密度林分平均木不同高度处直径的模拟值与实测值十分接近，且当林分密度为3 333株·hm-2时，树干削度最大，而当林分密度为10 000株·hm-2时，树干削度最小，总体上，树干削度随着密度的增大而逐渐降低，降低的程度也随密度的增大而减小。

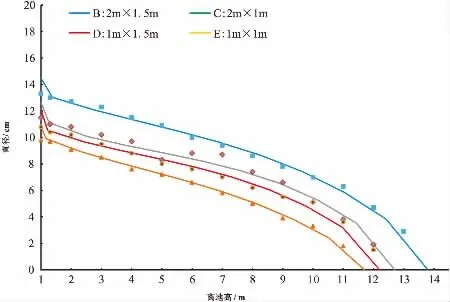
图1不同密度林分平均木模拟树干轮廓图Fig.1 Taper profiles for mean sample tree of different density with tree effects NLME model using fit data

2.3 包含密度因子的模型验证

表5列出了60株检验样本拟合不同形式下Kozak可变指数削度方程的统计量。在非线性回归拟合中，包含密度因子的削度方程的调整决定系数（=0.9804）高于不包含密度因子的削度方程的调整决定系数（=0.9801），且包含密度因子的削度方程的平均偏差（Bias=-0.0374）、均方根误差（RMSE=0.5063）、平均绝对偏差（MAD=0.3527）分别比不包含密度因子的削度方程的平均偏差（Bias=-0.0473）、均方根误差（0.5104）、平均绝对偏差（0.3537）有所减小。在混合效应模型中，包含密度因子的削度方程的调整决定系数（=0.9888）高于不包含密度因子的削度方程的调整决定系数（=0.9887），而且包含密度因子的削度方程的平均偏差（Bias=0.0184）、均方根误差（RMSE=0.3828）、平均绝对偏差（MAD=0.2534）分别比不包含密度因子削度方程的平均偏差（Bias=-0.0271）、均方根误差（0.4401）、平均绝对偏差（0.2568）有所减小。因此，在可变指数削度方程中构建密度因子，是可以提高模型的预估精度，降低模型预估偏差，并且利用非线性混合效应拟合的包含密度因子的Kozak可变指数削度方程的预估精度最高，调整决定系数达到0.9888。最终选择的模型方程式如下式：

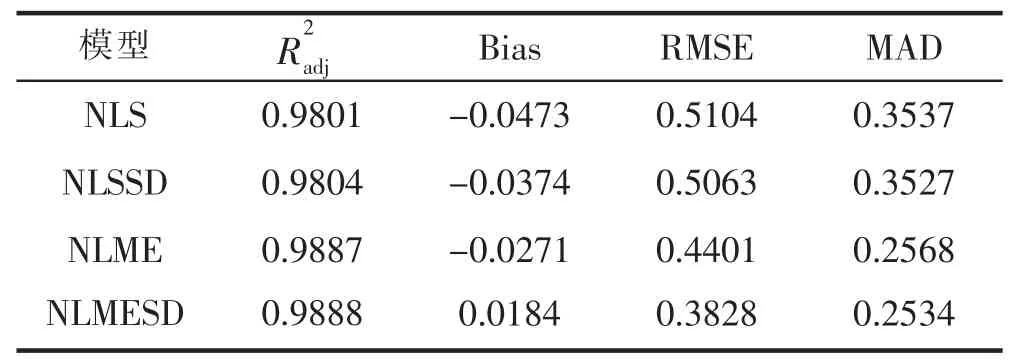
表5 4种不同形式的Kozak(2004)模型的检验统计量Tab.5 Goodness-of-fit statistics of Kozak(2004)for the four different forms using validation data

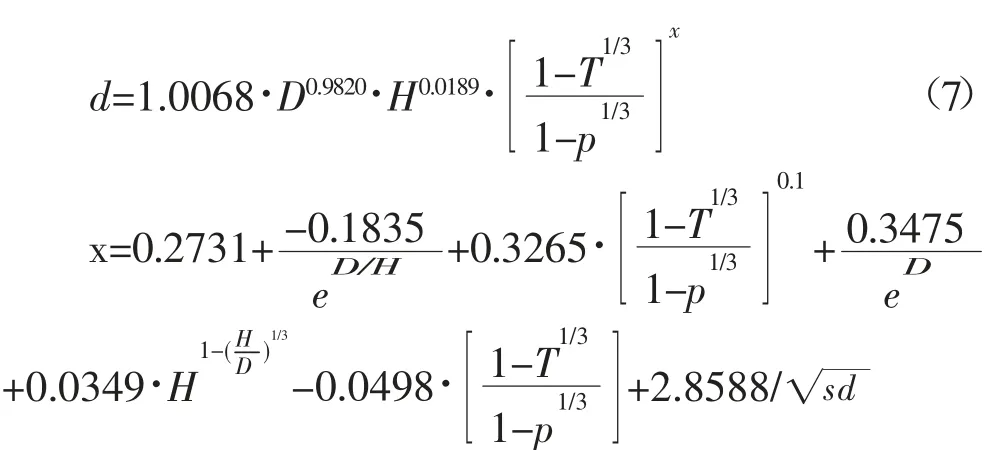
式中变量与式（6）相同。

为评价包含密度因子的Kozak模型对分段树干直径的预测能力，将检验数据中每株树的相对高度分为10部分。对于每部分直径的预测平均偏差和标准差进行分段统计（表6）。从表6可以看出，包含密度因子的Kozak基于样木效应的混合效应模型在0.1＜h/H≤0.5，0.7＜h/H≤1处的平均偏差为负值，说明模型预测值偏高，在树干中部（0.0＜h/H≤0.1）和顶端（0.5＜h/H≤0.7）处的平均偏差为正值，说明预测值偏低，而且在树干的0.9＜h/H≤1.0处为最高值，在0.7＜h/H≤0.8处为最低值。平均绝对偏差在树干的基部处的值为0.4833，是整个分段最高值，其次是树干的顶端处的值为0.2921，而在树干中部的平均绝对偏差较低，说明包含密度因子的Kozak模型在树干基部和树干顶端的预测值偏离真实值程度最差，在树干中部的预测值偏离真实值的程度较低。检验值的标准差在树干基部和顶端处存在最高值0.7540和0.6234，而其他部分的标准差值相接近，说明包含密度因子的Kozak模型在树干基部和顶端处预测值的离散程度较高，而其他部分预测值的离散程度较低。总体来说，包含密度因子的Kozak模型对整个树干的预测能力较高，但是对树干基部和顶端的预测精度稍低于树干中部。

为了评价包含密度因子的Kozak模型对不同密度林分内平均木的预估效果，选取检验数据中每个密度林分中的平均木，其中包括B密度（D=12.6 cm，H=13.5 m）、C密度（D=10.8 cm，H=13.0 m）、D密度（D=10.2 cm，H=11.6 m）和E密度（D=10.0 cm，H=12.0 m）。用包含密度因子的Kozak基于样木效应的混合效应模型对4个密度的平均木进行树干轮廓预估（图2）。由图2可知，不同初植密度林分中平均木的树干表现出不同的削度。初植密度为3 333株·hm-2的林分平均木的尖削度最大，并且随着密度的增大，林分平均木的削度在组间减小，减小的程度也随着密度的增大而逐渐减小，当初植密度为10 000株·hm-2时的林分平均木的尖削度最小。

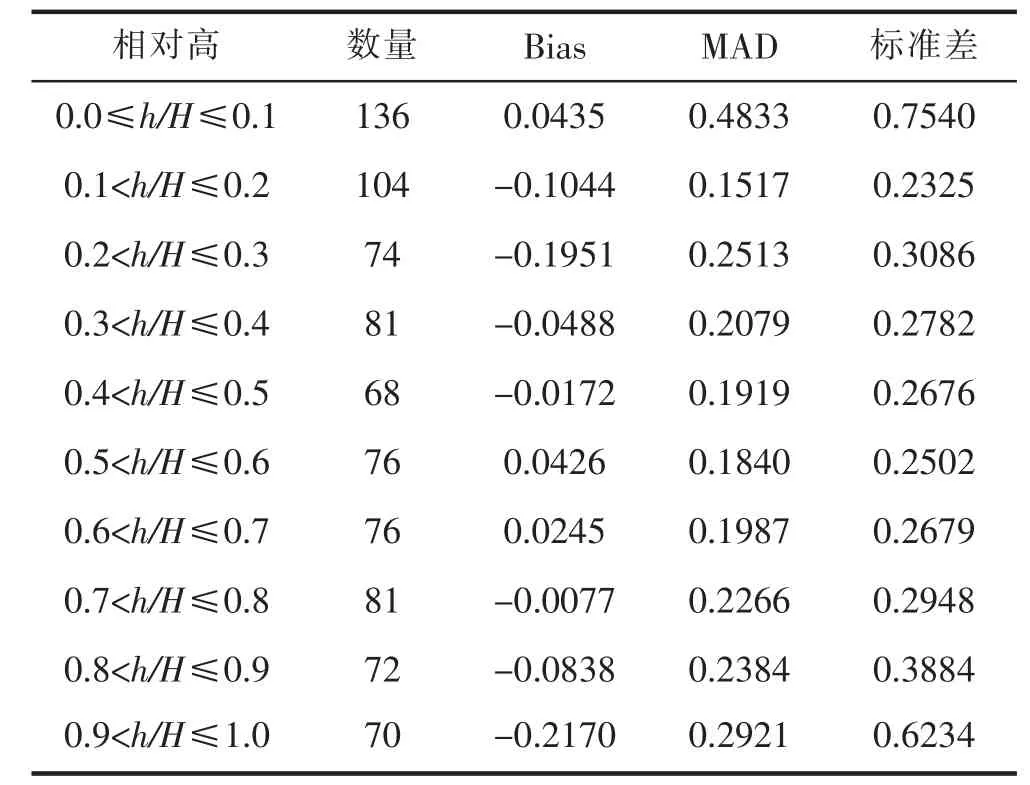
表6考虑样木效应包含密度因子的Kozak混合模型的分段检验统计量Tab.6 Examined statistics for Kozak with density of mixed model with tree effects in the different relative height classes

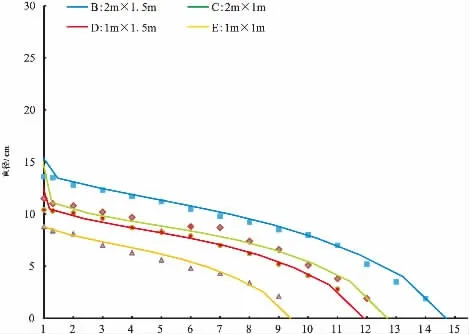
图2不同密度下平均木的Kozak模型检验树干轮廓Fig.2 Taper profiles for mean sample tree of different density in Kozak with tree effects NLME model using validation data

3 讨论与结论

大多数的削度方程以胸径（D）、全树高（H）、任意树干高度（h）和相对树高（h/H）为自变量，然而一些学者在削度方程中加入其他自变量，如冠长率、冠幅等[2]，研究结果表明加入其他自变量之后，并没有对削度方程的拟合精度产生显著影响，并且模型模拟的精度取决于树干直径测量的准确度。但亦有研究表明，在削度方程中加入林分经营因子或其他自变量之后，削度方程的精度有显著提高[16,18-20]，本研究结果亦表明林分密度因子引入后拟合精度有所提高。此外，林分密度因子引入后，通过削度方程预估的不同密度林分内林木干形随密度的增大，削度逐渐减小，且减小的程度也随着密度的增大而逐渐降低，这与Sharma and Zhang的研究结果相同[4]，表明在初植密度较大的林分中，由于林木激烈竞争而使树冠更多地朝向顶端收缩导致树干的干形更为通直饱满，而在初植密度较小的林分中，竞争相对较小，树冠占全树高比重更大，树干尖削度则相对较大。

本研究以Kozak削度方程为原型，探讨了杉木包含密度因子的可变指数削度方程的构建过程及效果，比较得到了最优的包含密度的指数表达形式，发现引入密度因子后，无论是非线性回归还是混合效应模型，削度方程的拟合精度均有所提高，而应用混合效应模型对包含密度因子的削度方程进行预估时较非线性回归模型更优。构建的杉木可变密度可变指数削度方程在树干中部预估值的平均绝对偏差较低，而在树干基部和顶端的预测效果较差，且树干削度随初植密度的增大而降低，降低的程度随着密度的增大而减少。所建立的杉木可变密度可变指数削度方程拓展了杉木干形预估的灵活性与准确性，可满足杉木单株商品材及林分材积的高精度预测需求，亦能为杉木材积表研制提供可靠途径。