基于点云数据的固体随形填隙垫片快速成型方法

葛恩德，张博添，刘学术，李汝鹏

(1. 上海飞机制造有限公司，上海 200120；2. 大连理工大学汽车工程学院，辽宁 大连 116024)

0 引言

碳纤维复合材料在航空领域的应用愈加广泛，其应用范围已由非承力、次承力构件发展到主承力构件，如飞机的翼盒、机身等结构。然而由于复合材料的各向异性特点，复合材料制件在成型后极易产生翘曲变形，导致在本应完全贴合的装配界面处形成装配间隙[1]。装配间隙的存在会影响结构的承载性能及服役寿命，因此，对于民用飞机等飞行器，为满足适航要求必须对装配间隙进行充填补偿，所以对装配间隙进行准确测量是实现装配间隙精准补偿的前提和基础。

传统的装配间隙测量方法是利用塞尺等测量工具对贴合面处的装配间隙进行手工测量，不仅效率低，而且精度差。特别是对于飞机上的盒段类结构，在其预装配后会自然形成封闭、半封闭区域，致使手工测量装配间隙不可达，是民用航空结构件连接装配中面临的现实挑战。而数字化检测技术近年来随着计算机技术的发展在各行业得到了越来越广泛的应用。在飞机装配方面，文献[2]通过数字化测量技术与柔性工装相互配合来保证柔性工装的定位精度，并缩短飞机装配周期。文献[3]设计了一套专用夹具用来测量低刚度构件，该装置在模拟装配件配合面的同时获取构件关键点几何坐标用于评估构件成型精度。文献[4]提出了基于机器视觉测量原理的非接触式数字化测量方法，相比于两点式数显内径千分尺和三坐标测量机两种传统测量方法，该方法的测量效率和重复性精度均明显提高。文献[5]提出了一种可用于柔性构件受载变形的预测方法，通过该方法可以对预装配后结构件的装间隙进行评估。文献[6]提出了一种基于零件测量的数值计算方法，该方法能够检测单个构件装配前后之间的形状差异，主要侧重于将测量数据集成到仿真过程中。文献[7]提出了一种新的柔性配准方法，从而将制造缺陷与构件几何变形加以区别。文献[8]针对制造缺陷附件的扫描点可能引起检测误差的问题，基于曲率和Mises应力提出了一种过滤方法以实现对成型缺陷的判断，继而提高成型精度评估的准确性。文献[9]提出了一种装配间隙数字化测量方法，并通过对比装配间隙模型验证了该方法的有效性。文献[10]提出利用探头与测力传感器并结合有限元仿真的方法预测柔性构件几何形状。

目前，数字化测量方法已被广泛应用于几何尺寸测量及成型精度检测等方面，重点关注的仍是构件制造几何精度，对于实现构件连接装配中间隙数字化测量的研究还相对较少，已报道的研究成果仍缺少足够的精度验证说明。因此，本文针对碳纤维复合材料构件装配连接时需要对装配间隙进行测量并补偿的实际需求，提出一种基于点云数据的数字化测量方法及固体填隙垫片快速成型方法，特别是对于点云数据虚拟装配精度差的难题，提出通过对定位螺栓关键特征提取实现精准装配的操作方法，实现了装配间隙的数字化测量及填隙垫片的快速成型，并通过试验验证了所提方法的可行性。

1 点云数据获取及预处理

1.1 点云数据获取

选取的复材构件如图1所示。该构件由复合材料制件组成，包含两个肋(肋A和肋B)及上下两块复材板，其中上板一分为二，标记为A和B。两个肋及上板A和下板提前利用螺栓连接，形成组件Ⅰ。上板B作为独立组件最后装配，称为组件Ⅱ。由于肋在成型过程中存在一定的几何变形，致使其与上板B之间存在一定的装配间隙(如图中放大图所示)，通过对比同一位置处手工测量与数字化测量结果可以评价数字化测量方法的准确性。

图1 实验用复合材料构件

上板B与复材肋之间采用螺栓连接，螺栓孔直径为4 mm，理论间距为35 mm。对于此实验件，如何准确定位装配组件点云数据是面临的实际困难之一。这主要是因为点云数据通常来自被测制件的表面，对于上板B而言，其为平板，局部无其他明显特征，如何准确定位其与肋的相对位置关系则是必须解决的关键问题。虽然理论上通过螺栓孔可以实现二者的准确定位，但由于在对其扫描测量时很难在螺栓孔孔壁上采集到数据点，因此对于仅有平面点云数据的螺栓孔而言，考虑到测量时噪音点的影响，根本无法准确给出螺栓孔的中心点位置，也就无法直接用于后续的虚拟装配操作。为解决这一问题，提出利用定位螺栓辅助定位的基本思想，即在对构件进行扫描测量时，在用于定位的螺栓孔位置增加定位螺栓，通过对螺栓的扫描获取定位信息，用于后续的虚拟装配操作。实验中装配组件定位孔及定位螺栓编号如图2所示。由于原复材制件表面呈深色且反光严重，严重影响数据采集效果，因此在其表面喷涂白色涂料，同时粘贴标志点(图中白色圆点)，用于提升数据采集精度。

(a) 组件Ⅰ(b) 组件Ⅱ图2 定位孔选择及定位螺栓编号

利用Einscan Pro 2X照相式三维扫描仪对装配组件进行扫描测量，扫描模式为手持精细扫描，其分辨率最高可达0.2 mm，拼接方式为标志点拼接，所获取的原始点云数据模型P如图3所示，包含的数据点个数分别为PⅠ=1 956 293和PⅡ=1 531 932。测量中不可避免的存在噪音点，同时测量数据中也包含了装配组件周围环境；此外，装配间隙仅存在于上板B与肋上缘的配合区域。鉴于测量数据中包含大量无关数据，因此需要对点云数据进行适当精简，以提升后期数据处理速度。

(a)组件Ⅰ点云(b)组件Ⅱ点云图3 装配组件原始点云数据

1.2 点云精简

对点云数据的预处理包含多种方法，如滤波、杂乱点去除等。但无论何种处理方法都会在去除噪音点的同时对真实数据点产生一定的影响。为验证所提方法的鲁棒性，本次实验中对于点云数据的精简仅限删除与装配间隙评估无关的点云数据，而不做任何点云数据平滑处理。

依据上述思想，对原始点云数据精简后得到的点云数据模型如图4所示。精简后的数据点个数分别为PⅠ=368 572和PⅡ=516 432。由于上板B为平板，其特征不明显，为保证测量效果，存在针对某区域重复测量的过程，造成数据点密度大于组件Ⅰ。

(a) 组件Ⅰ精简点云(b) 组件Ⅱ精简点云图4 精简后的点云数据模型

精简后的点云数据细节图如图5所示。首先对于定位螺栓仅保留螺帽部位的数据点。其次，数据点中包含很多孔洞，这些孔洞一方面是由于螺栓孔的存在而产生的，另一方面是由于粘贴的标志点造成的。如前所述，对点云数据的精简完整的保留了扫描数据的原始特征，因此，这些孔洞得以保留。

图5 精简后点云数据细节图

2 点云数据虚拟装配

合理确定装配组件点云数据相对位置关系是装配间隙评估准确与否的关键所在。由图5可知对于连接孔或圆形标志点，由于测量时误差的存在以及噪音点的影响，点云数据都无法准确呈现圆形特征，因此很难准确利用点云数据提取圆孔位置信息。而对于定位用的螺栓帽，其本身是圆柱形，且尺寸较大，测量时能获得足够多的数据点，因此可以利用这些数据点所能提供的信息实现装配组件相对位置的确定。

利用圆柱特征实现装配组件定位的基本思路为：①利用测量数据点进行圆柱拟合，获取圆柱轴线信息，即定位孔轴线信息；②利用获取的圆柱轴线信息实现装配组件点云数据空间位置的确定，即虚拟装配。

2.1 定位信息获取

定位信息获取的工作流程为：

(1)在装配组件点云数据P中的螺帽部位任选一点p0(x0,y0,z0)∈P；

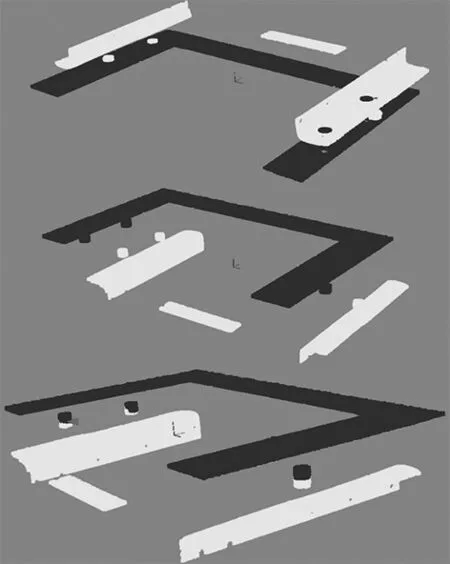
(2)以p0为中心，r为半径确定p0的一个邻域N，N(p0)={q∈P|dis(q,p0)

(3)采用Ransac算法对点集N(p0)进行圆柱拟合，获得圆柱轴线向量A，在A上选取一点C(xc,yc,z0)；

(4)计算p0与C之间的距离λ，λ=dis(p0,C)；

(5)如果λ<λuser，λuser为设定的阈值，计算终止，即C为定位螺帽轴线上一点，轴线法向量为A；否则，令p0=C，返回第(2)步。

利用上述方法获取的定位螺帽轴线示例如图6所示。左图中红色的点为初选点p0；中间图中红色的点为p0的领域N(p0)，即用于圆柱拟合的数据点；右图为计算后的俯视图，图中红色的中心点为轴线上一点C。由图中可知，点云数据中存在一定的噪音点，但并不妨碍定位信息的获取。

(a) 初选p0 (b) N(p0) (c) 轴线C点图6 定位孔轴线获取示例

利用上述方法可获得装配组件定位信息，标记为AⅠ1、CⅠ1、AⅠ2、CⅠ2、AⅡ1、CⅡ1、AⅡ2、CⅡ2，其中A表示轴线，C表示定位轴线上一点，下标Ⅰ和Ⅱ分别表示装配组件，上标1和2分别表示定位螺帽的编号。

2.2 基于定位螺帽的虚拟装配

对于装配组件点云数据空间位置关系的确定，可以根据如下操作完成：

(1)手动调整PⅠ和PⅡ，使其位置关系与配合后位置大体相符，且组件的主轴线方向尽可能与坐标轴相同，如沿z轴方向；

(2)利用上节所述方法获取定位螺帽信息；

(3)根据CⅡ1与CⅠ1对应关系，对点云数据PⅡ进行坐标变换，使CⅡ1与CⅠ1重合；

(4)调整PⅡ姿态，使AⅡ1与AⅠ1重合；

(5)令CⅡ2与CⅠ2的主轴方向坐标相同，如z相同，对PⅡ进行坐标变换使调整坐标后的CⅡ2与CⅠ2重合。

利用上述方法对装配组件进行虚拟装配过程如图7所示。图7中的上图为导入点云数据后的初始状态；中图为手动调整装配组件位置关系后的效果图，图中组件的空间位置关系与装配后的状态相同，即组件Ⅰ在下方，组件Ⅱ在上方，z轴为两组件的主方向；下图为虚拟装配后的效果图，此时由于噪音点的存在，仅有部分定位螺栓数据点显示为重合，但并不会对装配间隙评估结果产生影响；同时两个装配组件由于定位螺栓的影响，并未真正的实现配合面基本重合，而是在二者之间存在一段平移距离，在计算装配间隙时需要予以考虑。

图7 虚拟装配示例

3 装配间隙评估

3.1 装配间隙尺寸计算

对于虚拟装配后的点云数据而言，装配间隙即为配合面点云数据间的距离，其计算方法如下：

(1)对于PⅠ中的每一点p0∈PⅠ，根据2.1节中介绍的方法确定该点一邻域N(p0)；PⅠ中的所有点都处理后，则退出；

(2)采用最小二乘法对N(p0)进行平面拟合，获得该平面的法向量n(p0)；

(4)以n(p0)为向量，p0为线上一点定义直线L，选择点集Q={q∈PⅡ|dis(q,L)

(5)计算Q的形心Cq，则构件在p0点处的间隙尺寸g(p0)为g(p0)=dis(p0,Cq);

(6)返回第(1)步。

装配间隙为配合面间的最小距离，因此需要根据评估点的法方向进行计算。所以，步骤(1)和步骤(2)是用于获取法方向；步骤(3)是用于判断点p0是否处于配合面处，主要是依据处于配合面处的点的法向量与组件主方向基本一致的事实进行判定；步骤(4)和步骤(5)则是用于计算间隙尺寸。

由于上节所述虚拟装配方法中装配组件间存在着一段未知的平移距离g0，因此需要对计算的装配间隙尺寸进行调整。对于g0的计算可根据公式g0=argming(pi∈PI)进行，对于所有的装配间隙尺寸的计算结果再减去g0后可得到真实的间隙尺寸。

3.2 装配间隙模型重构

经过装配间隙尺寸计算后，可利用间隙尺寸不为零的点云重建装配间隙三维几何模型。本文采取对点云数据进行三三组合形成三角面片的方法来重构间隙模型，图8为实验样件的装配间隙几何模型，左图为曲面模型，右图为网格模型。由图中可见对于实验样件，其装配间隙极不均匀，同时也证明本文所提装配间隙评估方法的实用价值。

图8 装配间隙三维模型

3.3 填隙垫片加工轨迹生成

在得到装配间隙三维几何模型后，可利用该模型直接生成G代码，用于驱动机床完成填隙垫片的快速加工成型。

4 实验验证

4.1 间隙评估方法精度验证

首先，采用定位螺栓信息进行验证。如图2所示，对于定位螺栓(孔)1和2，其孔间的理论距离为70 mm。由于加工过程中可能存在的误差，通过游标卡尺对其测量可获得其实际距离。测量结果如表1所示，由两个人分别对定位孔间距离测量3次，取平均值作为测量结果，将两个人的测量结果取平均值作为最终的定位孔间距。据此可知，两个定位孔之间的距离为72.34 mm。

表1 定位孔间距测量数据表(单位：mm)

利用本文2.1节中所提的定位信息获取方法获得的定位点坐标信息如表2所示。需要说明的是：①表中的定位孔坐标具体数值与装配组件初始位置相关，因此其数值本身并无太多实际意义，但可用于计算组件上某些几何信息，如孔间距。②由于实验中所选取的装配组件主方向为z轴方向，且定位孔z坐标的计算与初选点相关，因此其本身数值也无参考意义，故表中未给出具体数值。依据表中数据可知孔间距为71.25 mm，与实测数值 72.34 mm的相对误差约为1.5%，证明所提方法的有效性。

表2 定位孔孔心评估数据表 (单位：mm)

4.2 填隙垫片快速成型

由于机床在加工填隙垫片时，对垫片的厚度有较高的要求。当垫片厚度过小时(如小于2 mm)，机床在加工过程中极易因加工热导致垫片变形，继而影响加工质量甚至无法完成加工操作。为完成所提方法的验证，特选择一个间隙尺寸较大的样件来完成填隙垫片的加工验证。

选用的实验样件如图9所示，上面为一块复合材料板，有着严重的翘曲变形，同时该板人为设计了两个凸槽；下面为一块金属平板。该构件的间隙具有典型的不规则特征。

图9 实验样件图

利用前文所述方法，可快速生成装配间隙几何模型和加工轨迹，如图10所示。图中深红色图形为装配间隙几何模型，浅蓝色曲线为加工轨迹。这里需要说明的是给出的间隙模型为调整间隙厚度前的模型。

图10 装配间隙模型及加工轨迹图

在人为增加垫片厚度后，利用生成的G代码，可驱动机床完成填隙垫片的加工，结果如图11所示。由图中可见，生成的填隙垫片与原始模型吻合很好，证明了方法的可行性。

图11 快速成型的填隙垫片

5 结论

本文提出了一种基于点云数据模型的填隙垫片快速加工方法，介绍了一种利用定位螺栓实现点云数据装配组件的操作流程，给出了装配间隙计算过程及填隙垫片快速成型方法，最后利用实验样件典型特征数据对本文所提方法进行了验证，根据实验结果可见：①本文所提的装配组件定位信息获取方法是有效的，其相对误差约为1.5%；②利用本文所提的装配间隙评估方法获取的数据可快速形成随形垫片加工G代码，实现随形垫片的快速成型。