基于二元正态分布匹配和非线性优化的激光SLAM研究

陈智君，郝 奇，伍永健，郑 亮

(1.哈尔滨工业大学芜湖机器人产业技术研究院，安徽 芜湖 241000； 2.芜湖哈特机器人产业技术研究院有限公司，安徽 芜湖 241000)

0 引言

目前市场上的AGV大多数是红外引导、磁条导航和二维码导航，这些有着非自主移动、路径固定、安装费时和成本高的缺点。激光SLAM和传统定位方法不同，激光雷达采集到的环境信息是一帧帧离散的、具有角度和距离信息的点，被称为激光帧。激光SLAM系统需要对相邻时刻的激光帧进行帧间匹配或与地图进行匹配，计算AGV的实时位姿，并使用实时位姿和激光帧对概率地图进行更新得到导航地图，来实现后续的路径规划和自主导航[1-2]。

现有最强大的激光SLAM算法主要是基于非线性优化的Hector和基于图优化的Cartographer。Hector是基于多分辨率地图的非线性优化，其算法在多分辨率地图中容易陷入局部极值，而且多图层的更新也耗大量时间[3-4]。Cartographer前端匹配暴力搜索候选项，耗费大量时间，而且最优位姿仅基于概率地图的优化使得鲁棒性不足[5]。对于现有方法中存在的问题，本研究提出了基于二元正态分布匹配和非线性优化的激光SLAM算法，实现了一个实时激光SLAM算法，并在AGV平台上进行了测试。

1 AGV激光SLAM算法框架

该算法主要运行有三个线程，分别是雷达数据预处理，激光帧匹配和地图更新和显示线程，具体框架和流程如图1所示。

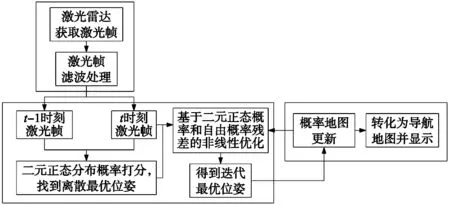
图1 激光SLAM算法流程图

第一个是雷达数据预处理线程，用于从激光雷达获取激光帧，并对激光帧进行滤波处理，包括去除离群点和降采样。

第二个线程是激光帧匹配线程。首先，第一帧雷达激光帧需要初始化自由概率地图；其次，将t-1时刻激光帧以一定栅格尺度进行二元正态分布化，对落入激光点超过一定数量的栅格计算其二元正态分布参数。然后，由t时刻激光帧在t-1时刻激光帧位姿态的相关性区间进行投影和概率打分，通过离散寻优，找到离散点集最优解；之后，由二元正态分布概率密度函数和自由概率残差构建非线性最小二乘目标函数，使用高斯牛顿法迭代求解最优位姿。

第三个线程是地图更新与显示线程。用于将匹配线程得到的最优位姿投影到概率地图，进行地图更新，最终转化为导航地图并进行显示。

2 激光雷达数据预处理

如图2a所示，激光扫描到物体的边缘会发生拖尾，这些无效点影响匹配的稳定性，因此在匹配前使用半径滤波器去除这些离群点。半径滤波器遍历每个点，计算该点到临近点的距离，如果距离大于预设值，认定为离群点，然后进行剔除，剔除后如图2b所示。

图2b是滤波后的图，但是仍然有很多点，SLAM地图栅格尺寸为5 cm，同一个栅格内点数非常多，极大影响匹配和更新效率。因此还需要进行体素滤波，在同一个栅格内只保留一个点，在保证点云微观特征的基础上降低点云的密度，提高匹配效率，滤波后如图2c所示。

(a) 原始激光帧 (b) 剔除离群点 (c) 体素降采样图2 激光点云滤波图

3 二元正态分布化及离散寻优

该方法的目的是初步计算AGV在t-1时刻到t时刻的位姿增量，就是计算两帧激光帧点云的旋转平移变换。该方法是离散位姿集通过二元正态分布概率函数打分找到一个最优位姿，给最后的非线性优化提供一个良好的位姿初值。

3.1 二元正态分布化激光点云

将t-1时刻滤波后的激光帧点云栅格化，计算每个栅格内激光点集的位置均值:

(1)

可得该栅格的协方差矩阵：

(2)

令pi(x)=Pi-mean，∑=covMatrix。那么可得二元正态分布匹配的归一化概率F(x):

(3)

其函数分布如图3所示，然后将t时刻激光点云s以一定位姿投影到t-1时刻的二元正态分布化点云地图上，那么函数计算的点云归一化概率得分越高，两点云重合度越高，认为匹配成功。

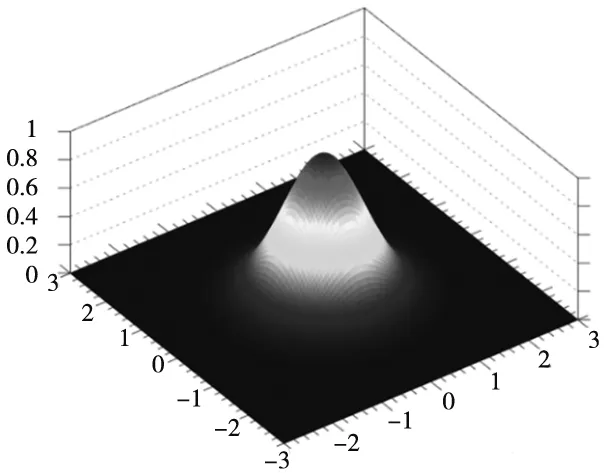
图3 二元正态分布归一化概率图

3.2 离散寻优

已知室内AGV的工作最大线速度linear_v和最大角速度ang_v，再已知雷达频率为10 Hz，那么在t-1时刻到t时刻，AGV单向移动距离不超过0.1*linear_v，旋转角度不超过0.1*ang_v，那么离散寻优的窗口范围应该是以t-1时刻机器人的位姿POSEt-1为中心，以0.2*linear_v宽度的方形窗口搜素位置，以0.2*ang_v角度范围搜索姿态角，搜索范围如图4所示。

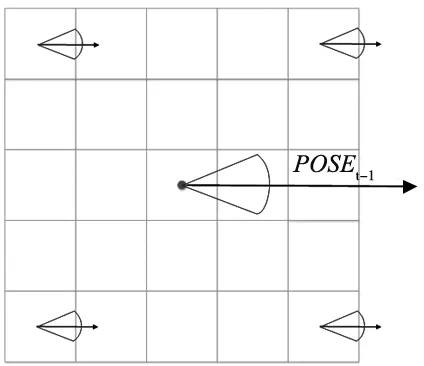
图4 搜索窗口范围和角度

已知栅格分辨率下，雷达旋转角度步进的最高分辨率是激光扫描的最远点旋转一个地图栅格尺寸的角度，那么由余弦定理可得：

(4)

其中，res是所建栅格地图的分辨率，max是激光雷达扫描的最远点距离。

如果暴力搜索所有位姿，那么可得匹配位姿候选项数目:

(5)

假设AGV雷达一帧最远点距离为30 m，所建地图分辨率为0.05 m，机器人最大速度1 m/s，旋转最大速度180 °/s。如上公式可得角度候选项数目达400，位置候选项25，总候选的离散位姿数目达到10 000，匹配会耗费大量时间。

由于匹配方法使用二元正态分布打分，在最佳匹配角度上得分最高，离真实角度越远，二元正态分布打分就越低。因此在找最优角度时，使用如图5方法，在每一个栅格内先使用较大的搜索角度步进值ang_step，插值寻找最优角度angle_n，然后缩小搜索范围，同时缩小角度步进值。最后一层使用公式(4)得到的最小分辨率角度遍历，得到最优角度。

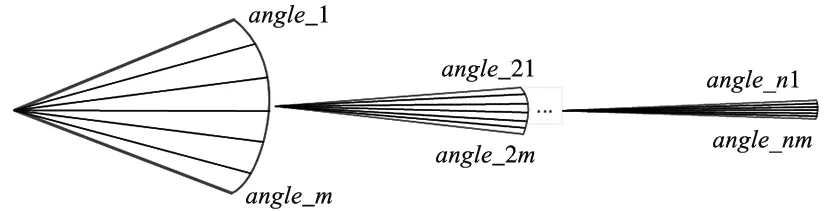
图5 多分辨率搜索

概率地图使用双三次插值计算概率，再考虑到激光点的跳动偏差，角度步进的最低分辨率可跨过多个地图栅格，在此设为grid_a。那么由公式(4)可得:

(6)

设定每层缩小搜索范围为shrr倍，角度步进值缩小shra倍,那么总角度候选项为：

(7)

此方法在保证精度和稳定性的前提下，匹配次数大大减少，提高了匹配速度。

4 自由概率地图

4.1 自由概率地图表示与更新

概率地图的栅格有三种状态：未知，占据和自由。常用概率栅格地图未知概率为0.5，大于0.5表示栅格为占据状态，小于0.5表示为自由状态[8-9]。

本方法使用uint8的整形值(0～255)作为栅格的自由值，使用整形数据避免了效率低下的浮点型运算，提高了地图更新的效率。那么未知概率0.5对应的是27=128,大于该值的栅格认为自由，小于该值的栅格认为占据。在建图前，只需计算一次0～1的浮点概率对应的0～255整形值，后续不用计算只需查表即可。

自由概率地图数据包含了整个地图的自由概率值free_value、用栅格数表示的地图宽width和高height、世界坐标原点在地图坐标系中的坐标origin、地图栅格的分辨率resolution。

地图的更新方法如下，首先计算地图栅格优势概率：

(8)

设定栅格测量占据概率为pocc，对应优势概率为oddsocc。

设定栅格测量自由概率为pfree，对应优势概率为oddsfree。

那么任意一次地图更新，栅格优势概率计算公式如下，其中测量占据更新：

(9)

测量自由更新：

(10)

更新后的自由概率：

(11)

本方法通过如上公式预计算256个整形值更新后的自由值，在进行激光帧匹配和更新时只需要查表即可。

4.2 基于双三次插值的自由概率分布

占用栅格地图是离散的，不能求导，直接取栅格概率还会限制精度。因此对于任一激光点打在概率地图中的概率要进行双三次插值[10-12]。如图6所示，将单个栅格概率看作是周围16个栅格连续概率分布的一个样本，此时在激光点位置取的概率更精准，也能对位姿求导，方便后期的位姿优化。

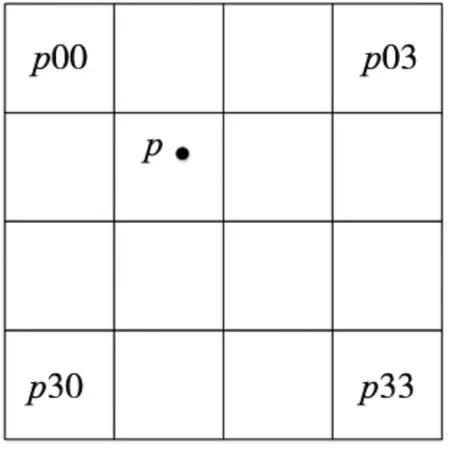
图6 激光点概率插值

双三次插值函数ω(p)如下所示：

(12)

其中设定p的浮点坐标为(r,c)，向下取整坐标为(row,col)，取小数部分坐标为(u,v)。

每行栅格的列坐标和行坐标分别为(1+v,v, 1-v,2-v)和(1+u,u,1-u,2-u)。

代入双三次插值函数ω(p)，分别得到4个列权重ki和4个行权重kj。

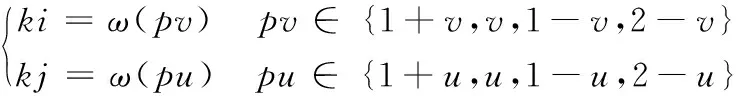
(13)

每个栅格概率的权重为kij=ki×kj，由公式(14)得到p点插值概率M：

(14)

计算地图概率相对于栅格坐标的导数∂M/∂p：

(15)

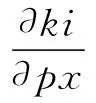
(16)

5 基于双概率残差的非线性优化

前面两节找到的是离散最优位姿，给如下的非线性优化方法提供初值，来迭代找到真实最优位姿。非线性优化方法很多，本方法选用较实用的高斯牛顿GN方法去优化，迭代速度较快，全局收敛较为精准稳定[13-14]。具体计算过程如下：

首先确定非线性最小二乘目标函数，如下所示，包含二元正态分布概率函数和概率地图残差项：

(17)

其中，pi(x)表示机器人在位姿x(px,py,pθ)处，激光雷达扫描点S(sx,sy)对应的栅格坐标。

(18)

目标函数在位姿x处进行一阶泰勒展开：其中，JF是二元正态分布函数F的雅各比矩阵；JM是双三次插值概率地图函数M的雅各比矩阵。

对Δx求导：

(19)

令H和fd为：

(20)

(21)

整理，化简可得Δx:

Δx=H-1×fd

(22)

其中，H和fd中的雅各比矩阵JF和JM如下：

(23)

(24)

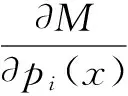
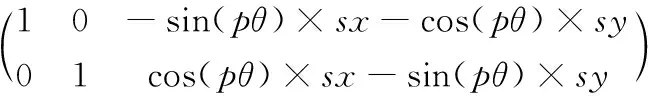
(25)

迭代求解Δx，当步进值小于设定阈值，迭代停止。

6 匹配和建图实验

6.1 实验设备和参数

本算法的实验运行环境是WIN10-VS2015，CPU为i5-4200M2.5GHZ。团队使用德国倍加福R2000激光雷达，其扫描范围360°，扫描半径50 m，在权衡AGV工作速度和精度的前提下，雷达选用频率10 Hz，采样率8400的参数进行。实验平台和环境如图7所示。

(a) 实验平台 (b) 实验室环境图7 实验平台和环境

6.2 基于离散寻优的多分辨率搜索实验

由于位姿候选项的位置分布是基于周围栅格的整形栅格坐标位置，AGV室内导航所需地图分辨率为5 cm，误差不会这么大，最佳匹配都是固定在一个栅格内部的不同角度，因此测试的是二元正态分布匹配的1000次角度标准差和时间均值，实验结果如表1所示。

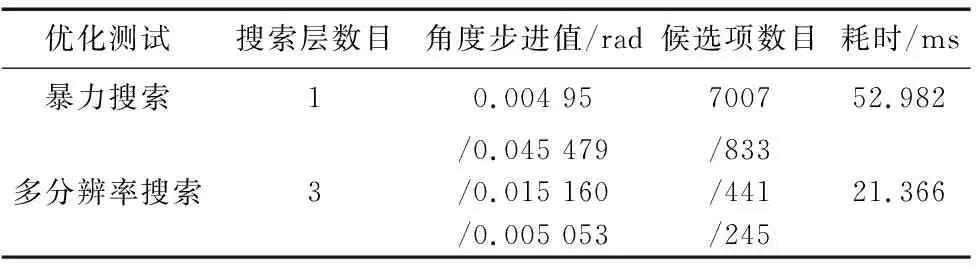
表1 二元正态分布匹配测试

由表1可知，暴力搜索的候选项数目为7007，多分辨率搜索3层的候选项总数为1519，约为暴力搜索的1/5。由于生成不同分辨率候选项要重新构建类对象，也要耗时间，因此最终匹配耗时约为暴力匹配的1/2，但也明显提高了匹配速度。

表2是暴力搜索和多分辨率搜索原地匹配1000次的精度测试输出结果，可以看出角度最大偏差和标准差基本一致，多分辨率搜索的时间明显减少。

表2 二元正态分布匹配精度测试

6.3 基于非线性优化的精度测试

如图8所示，SLAM算法是在WIN10-VS平台下实验效果图，左边是SLAM的同步定位和建图界面，右边的终端显示了包含离散优化和非线性优化的匹配过程。图9右侧终端其中一次显示离散优化用时20.051 m，输出位姿(7.083,3.056,0.003 165)。非线性优化使用离散位姿作为初值，优化后位姿为(7.078,3.060,0.003 069)，用时11.573 ms，结合其余数据处理时间，总用时45.455 ms。匹配时间在雷达10 Hz频率范围内，因此本算法可实时进行建图和定位，建图过程如图9所示，能看到地图概率更新由暗到亮的过程，越亮表示空间越自由。

图8 WIN10-VS平台下SLAM算法效果

(a) 位姿1 (b) 位姿2

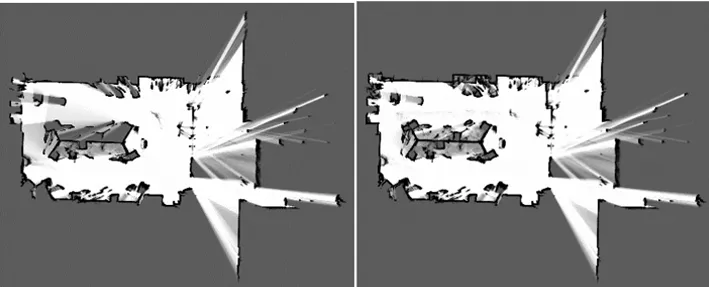
(c) 位姿3 (d) 位姿4图9 建图过程的地图更新

如表3所示，对本算法和另外两种算法进行匹配1000实验，程序均不使用序列化加速，算法测试平台保持一致。结果表明本算法精度相比Hector有明显提升，和Cartographer精度基本一致，但是本方法的平均耗时约47.9 ms，相比后两者有明显提升。

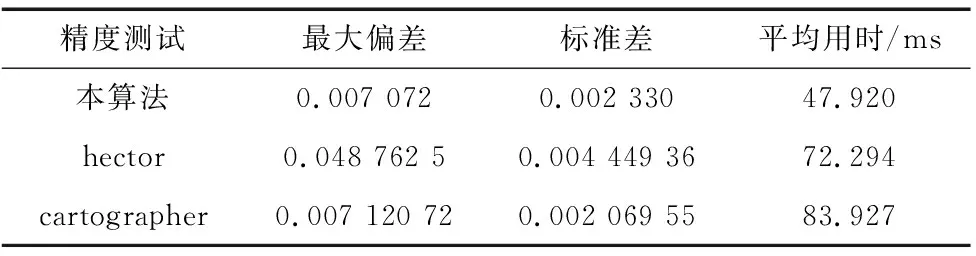
表3 算法的定位精度测量

本算法的位置最大偏差为7.072 11 mm，标准差σ为2.329 87 mm，精度高于主流的激光SLAM算法[3,4]。3σ的偏差为6.989 6 mm，都在1 cm内，满足AGV的工业精度要求。

7 结束语

本方法首先从激光雷达获取激光帧，对激光帧进行滤波处理，由第一帧激光帧初始化自由概率地图；其次将t-1时刻激光帧进行二元正态分布化，由t时刻激光帧在t-1时刻激光帧的相关区间进行投影和概率打分，找到离散最优解；之后由二元正态分布概率密度函数和双三次插值的自由概率残差构建目标代价函数，在离散最优解位置进行高斯牛顿迭代优化，得到最优位姿；最后将t时刻激光帧投影到地图中的最优解位姿，进行地图更新。实验测试结果表明，该算法匹配位姿精度高，建图效果好。在10 Hz激光雷达频率下，匹配更新只耗时约50 ms,3σ的偏差在7 mm左右，能满足AGV工业精度和实时性要求，该方法对AGV在实际工业环境的应用具有重要意义。