低压宽带电力线通信系统建模仿真分析
2021-09-28刘玉新李天昊孙梦娜
刘玉新,李天昊,孙梦娜
(辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105)
电网是国家能源产业链的重要环节,是各行各业正常运行的基础。世界每个国家对电力网络的发展都进行了思考,致力于提出具有能效高、绿色、安全、信息交互好的智能电网,提高电网运行水平。智能电网的建设需要通信技术的支撑,其中实现电网自动集抄的关键技术之一就是低压电力线通信技术[1-2],在低压配电网的基础上直接铺设,拥有分布广泛、布线简洁、成本价格低等优点。但是,电力线本身是为了传输电能,当作为信息传输媒介进行通信时,其效果并不理想[3]。因此,如何精确地建立符合实际的低压电力线通信系统模型,进而研究影响通信系统的因素,对于低压电力线通信的发展及使用有很大的理论研究意义。
国内及国外很多学者对低压电力线通信系统进行了大量研究。一些学者研究低压电力线信道:文献[4]介绍了低压电力线通信的两种信道模型——“黑盒”模型和二端口网络(Two Port Network,2PN)模型,指出了黑盒模型建模方法的复杂性,并验证了2PN模型代表电力线信道的准确性;文献[5]着重分析了室内低压电力线信道的回波模型,并对模型中多径数目、加权因子等参数的确认进行了拟合辨识。另一部分学者分析低压电力线通信系统中的噪声模型:文献[6]介绍了米特尔顿A类噪声模型(Middleton A)和循环平稳噪声模型,并比较了两种噪声模型对OFDM系统的影响;文献[7]利用有色背景噪声和窄带噪声的叠加模拟实际电力线信道上的噪声。大部分国内外学者主要聚焦于低压电力线通信系统的信道研究或者噪声研究,而有关信道特性对低压电力线通信系统性能的研究较少。
本文在2~28 MHz频带内,介绍了一种基于OFDM调制技术的低压宽带电力线通信系统模型。根据传输线(Transmission Line,TL)理论,建立电力信道的传输函数,以Middleton A类噪声模型模拟电力线信道噪声,重点分析噪声参数、电力线网络参数对信道特征和系统性能的影响。
1 低压电力线通信系统模型
OFDM调制技术拥有很多优点,如:频谱使用效率好、信道的均衡技术简洁、信号的调制跟解调容易实现、有效降低误码率等,很好地缓解了频带稀缺的问题;由于该技术可以缓解因多径衰落及多径反射等原因产生的频率选择性衰减问题,故在电力线通信[8-9]方面应用很广。因此本次通信系统采用OFDM调制方式,将信息比特映射到基带信号上进行传输,所建系统模型如图1所示。

图1 低压电力线通信系统模型
仿真模型如图1所示,信源(发送端)产生随机的信号数据流,通过OFDM技术调制进入含噪声影响的信道模型内;再通过OFDM技术对信道上的信号进行解调,在信宿端(接收端)获得相应的原始信号;最后,通过对比得到系统的误比特率。本文采用TL理论信道建模方法研究信道传输函数;又利用Middleton A类噪声模拟实际低压电力线信道上的噪声,使该系统模型更加真实。
2 低压电力线信道和噪声模型
2.1 基于传输线理论的信道传输函数模型
电力线通信系统中,载波数据流通过高频横电磁波在电力线上传输。普遍认为,每个单位长度的电力线都是均匀的,其上电压、电流根据频率的变化发生改变。单位的双导体传输线的等效电路如图2所示[10]。
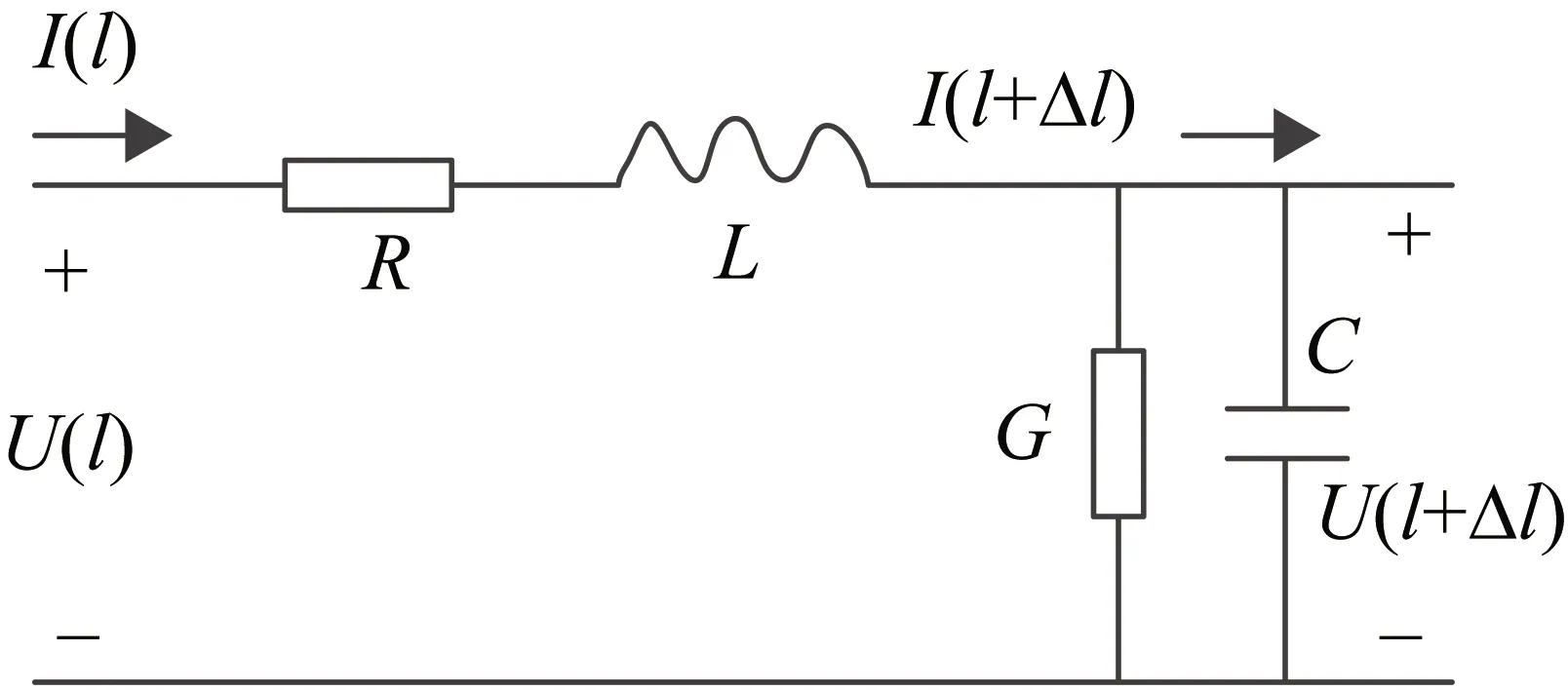
图2 单位均匀电力传输线等效电路
图2中R,L,C,G分别为单位长度下均匀电力传输线的电阻、电感、电容和电导。由基尔霍夫KCL,KVL定律:
(1)
化解微分方程得:
(2)
式中,A1,A2为待定系数,根据首端或末端条件得到;γ,Z0为复传输常数及特征阻抗,由单位电力传输线决定。
(3)
(4)
实际中电力线网络拓扑是复杂多变的多端口网络,2PN是其中一种最基础的结构。该结构中的电力线被认为是均匀的,能够采用TL理论求出其传输常数及特征阻抗。根据TL理论得到的电力线信道传输函数模型[11],是以网络的拓扑结构、不同电缆的长度与特征、负载阻抗等参数为依据计算得出传输函数。通过已知结构的电力网络,可明显地表征出网络传输参数对信道的影响,精准性高[12],与黑盒模型相比,不用对信道使用复杂的线性拟合辨识。
电力线网络拓扑可看作多二端口网络的级联。由TL理论得,每段均匀的TL都可以建模为2PN,传输矩阵为T,使用ABCD参量表示,与2PN中发送端和接收端的电压、电流有关。最简2PN结构如图3所示。

图3 最简2PN结构
图3中,V1,I1,V2,I2分别为2PN两端的电压和电流,其关系如下所示[5]。
(5)
式中,l,γ,Z0分别为均匀电力线的长度、传输常数和特征阻抗,如式(3)、式(4)所述。
由定义可知,电力线的传输函数为负载电压与电源电压的比值。
(6)
在给定载频下,电力传输线的电气特征能完全由单位长度下R,L,C,G表征。若主干网络的结构更为复杂时,可通过使用“并联分支线路等效并联负载”的方法,利用等效负载对子分支节点阻抗迭代更新,简化为主干网络并联负载结构,再将各子分支进行级乘得到整个网络的传输函数。
一种典型T网络结构如图4(a)所示。而基于传输线理论建模的一个重要特性是它可以让2PN的串联连接更容易,因此其等效网络拓扑如图4(b)所示。
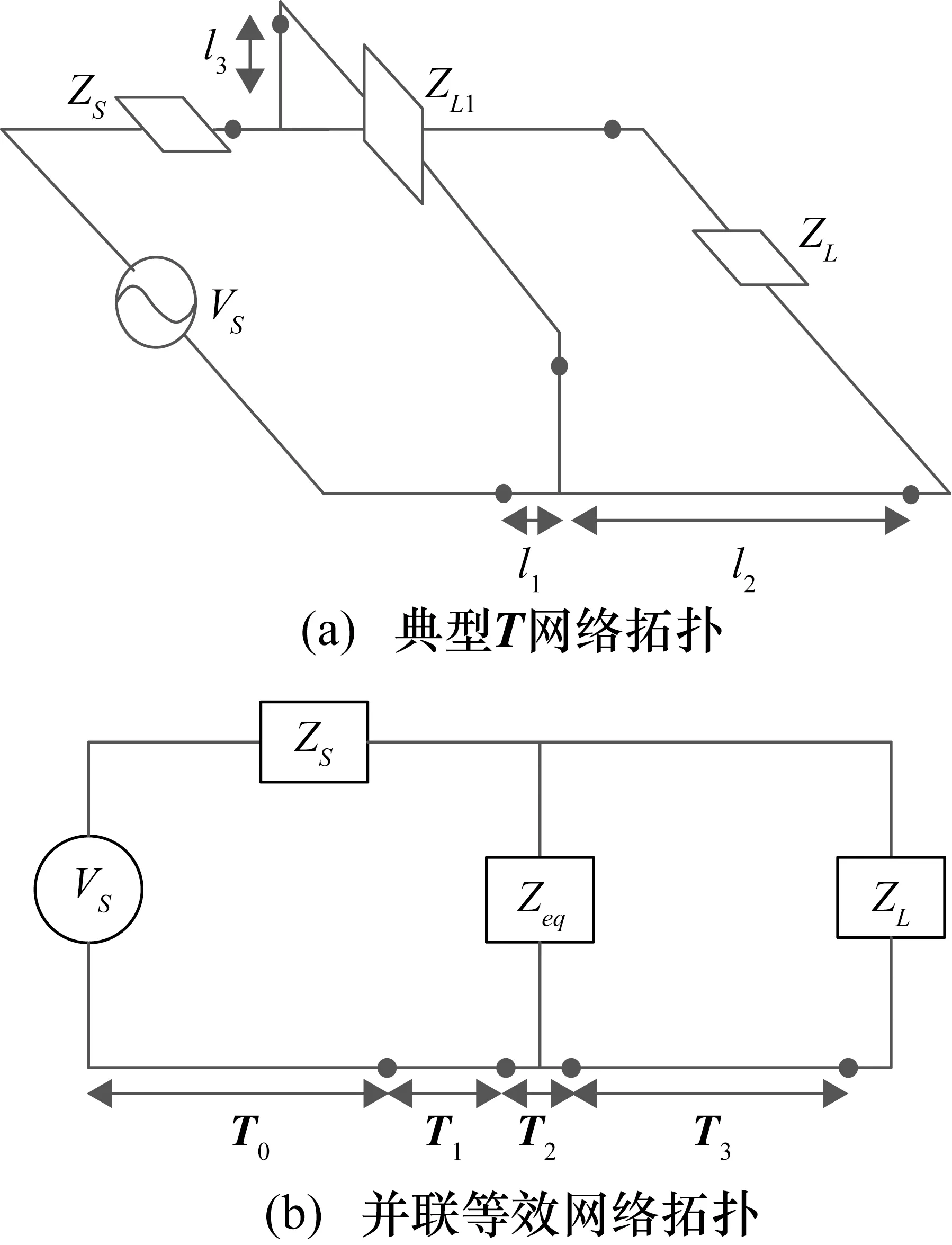
图4 并联传输线及其等效网络拓扑
图4(b)中等效阻抗Zeq可用下式计算。
(7)
式中,Z3,γ3为图4(a)并联部分的特征阻抗和传输常数。
图4(b)中的等效网络可以划分为4个子网络T0,T1,T2,T3串联结构,其中T1网络特征阻抗为Z1,T3网络特征阻抗为Z2。其计算步骤如下所示。
(8)
根据上述运算可得,通过各单结构的ABCD矩阵级乘可算出整个网络的ABCD矩阵。因此,典型T网络结构的总体传输矩阵可由以下关系给出:
(9)
在生活中,绝大多数居民楼内的电力线是由铜或铝构成,其中铜线使用最多,因此主要介绍铜质低压电力线的模型参数推导,如下所示。
① 电阻:
(10)
(11)
式中,σc为铜导体的电导率;μc为导体磁导率;a为导体半径;δ为集肤效应的集肤深度,是载频f的函数。式(10)中,当导体参数确定时,导体电阻随载频增加而增加。
② 电感:
(12)
电力线导体上的电感由内部自感及外部自感组成,统一称为互感。式(12)中,μ0为自由空间的磁导率;D为导体之间的距离。
③ 电容:
(13)
式中,ε是由介电材料决定的介电常数。
④ 电导:如果铜导体之间介电材料均匀,则
式中,σ为介电材料电导率。
由以上内容可知,在电力线材质、结构及数据信号频率确定的基础下,可以得到其传递函数。仿真中选取电力线横截面积为2.5 mm2,介电常数ε=1.52,特征阻抗Z0=234 Ω,电容C=17.5 pF/m,电感L=0.96 μH/m[13]。应用文献[14]中的参数于本文模型中,仿真比对如图5所示,其信道的幅频特性与文献[14]中的真实数据类似,故本文的信道建模方法可用于描述实际的信道模型。
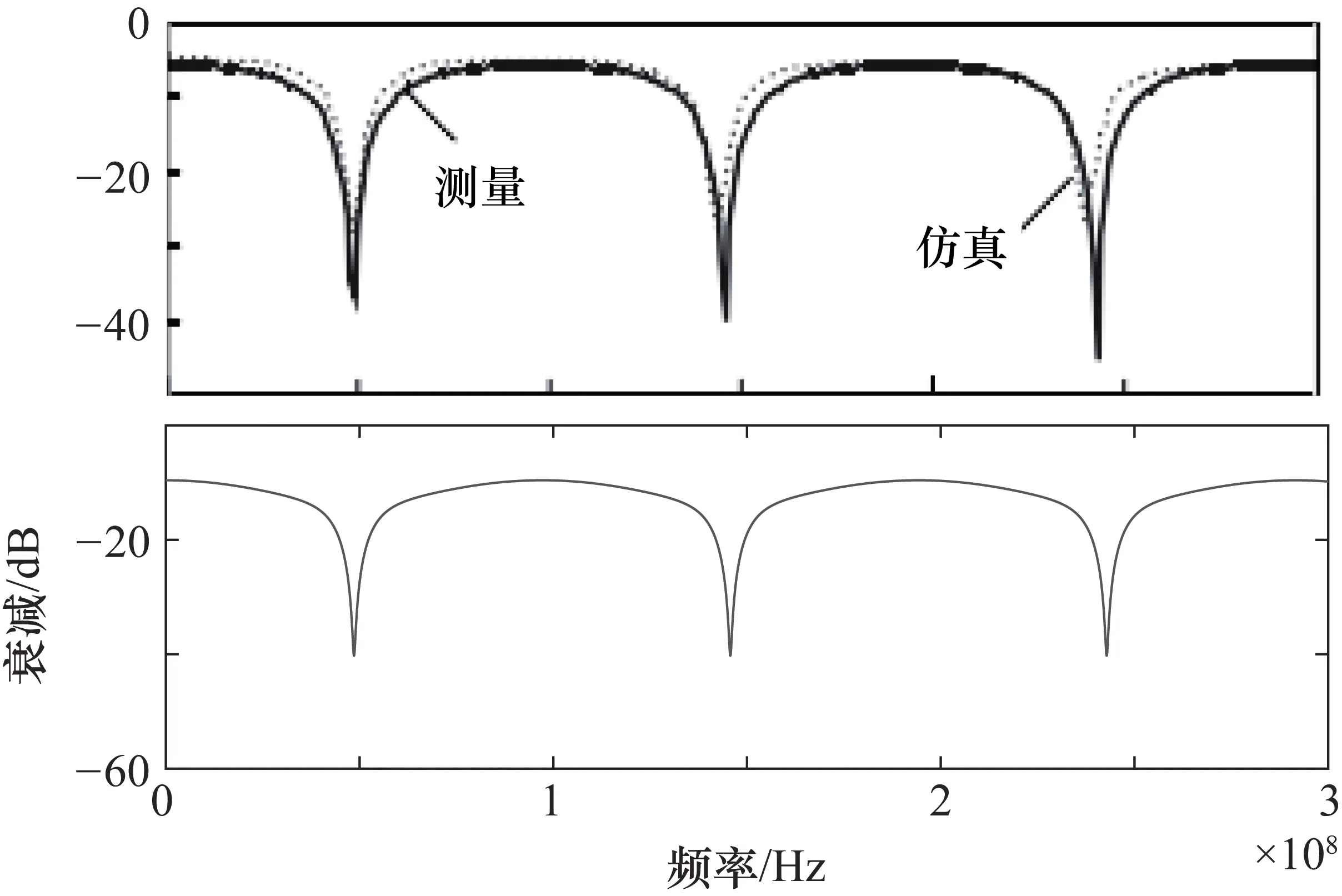
图5 信道模型仿真对比图
2.2 Middleton A类噪声模型
低压电力线信道有复杂的噪声干扰,无法通过高斯噪声来完全表示[15]。而米特尔顿A类噪声是由Middleton提出并以此命名的噪声模型[16-17],由于其概率密度函数(Probability Density Function,PDF)的简单性被广泛运用于电力线通信中,而且已经有大量的研究表明其对通信系统的影响。泊松分布用于描述单位时间内随机事件发生的次数,其PDF如下:
(14)
电力线通信中理想信道都是假设的,为了模拟电力线信道上的背景噪声和脉冲噪声,信道噪声的PDF可根据泊松过程表示为一个混合的零均值高斯项加权和的形式。米特尔顿A类噪声模型是由具有不同方差的高斯函数组合而成,其PDF表示为[8]
(15)
(16)
(17)
(18)
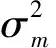
根据文献[8]所述:τ固定,A值增大时,米特尔顿A类噪声与高斯噪声类似;而A值减小时,该噪声就会类似于脉冲噪声。故选择合适的参数后,米特尔顿A类噪声可以有效地表示低压电力线上复杂的噪声情况。
3 系统仿真
在Matlab环境中仿真分析电力线网络参数及噪声参数对低压宽带电力线通信系统的影响,使用HomePlugAV标准参数,如表1所示。
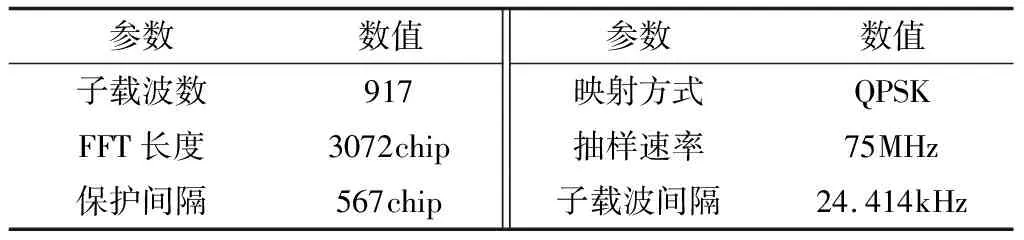
表1 OFDM调制仿真参数
3.1 噪声参数的影响
由第2节可得,Middleton A类噪声模型可根据高斯脉冲比τ和脉冲指数A两个变量特征表示。假设环境噪声总功率是固定得,电力网络得结构如图3所示,假定线路总长度是200 m,ZS=ZL=50 Ω,改变τ或A值研究其对系统信号误比特率的影响。
3.1.1 固定τ值
取τ=0.01,A值分别取0.1,0.5,1,10,软件仿真后,其结果如图6(a)所示。
图6(a)中,环境噪声功率、τ值固定,A值增加,表明信道中同一时间段内噪声源的数目增多,影响系统性能,使得信号的误比特率增加。然而,随着A值的增加,因为噪声功率的限制,使得其对系统性能影响逐渐变小。
3.1.2 固定A值
取A=0.01,τ值分别取0.01,0.1,1,软件仿真后,其结果如图6(b)所示。
由图6可知,当τ值不断增大,系统误比特率也逐渐增加。在噪声模型中τ值的增大,表明高斯噪声在整个噪声中所占比值增多,而高斯噪声对信号传输影响更大,故造成系统的误比特率增加。图6中,随着信噪比的逐渐增加,系统误比特率逐渐减小,这表明信号的频谱强度越强,噪声对信号传输的影响就越小。
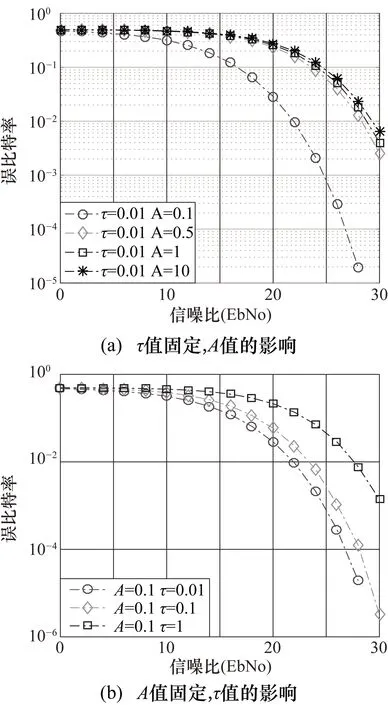
图6 噪声参数对系统影响
3.2 电力线网络参数影响
低压电力线通信时信号在传输过程中受到信道条件的严重影响,本节主要研究主信道长度、支路长度、支路负载等因素对信号传输的影响。系统仿真信道如图4所示,设ZS=ZL=50 Ω,噪声模型参数τ=0.01,A=0.1。
3.2.1 主干长度影响
本节设支路长度为20 m,支路负载为50 Ω,分支节点位于主信道中点。从发送端到接收端低压电力线主干长为100 m,200 m和300 m,得到其信道幅频特性与系统传输特性,如图7所示。
图7(a)是基于传输线理论信道建模方法所绘制的信道幅频特性。图中信道陷波频点的位置与主干长度无关,但随着主干长度的增加,陷波频点衰减增大。图7(b)显示了不同低压电力线主干长度对系统误比特率的影响,其中系统误比特率随着电力线长度的增加而增加。图中信噪比在12 dB以下时,主干信道的长度因素对信号传输影响较小;而信噪比在12 dB以上时,主干信道的长度对信号传输有较大地影响。
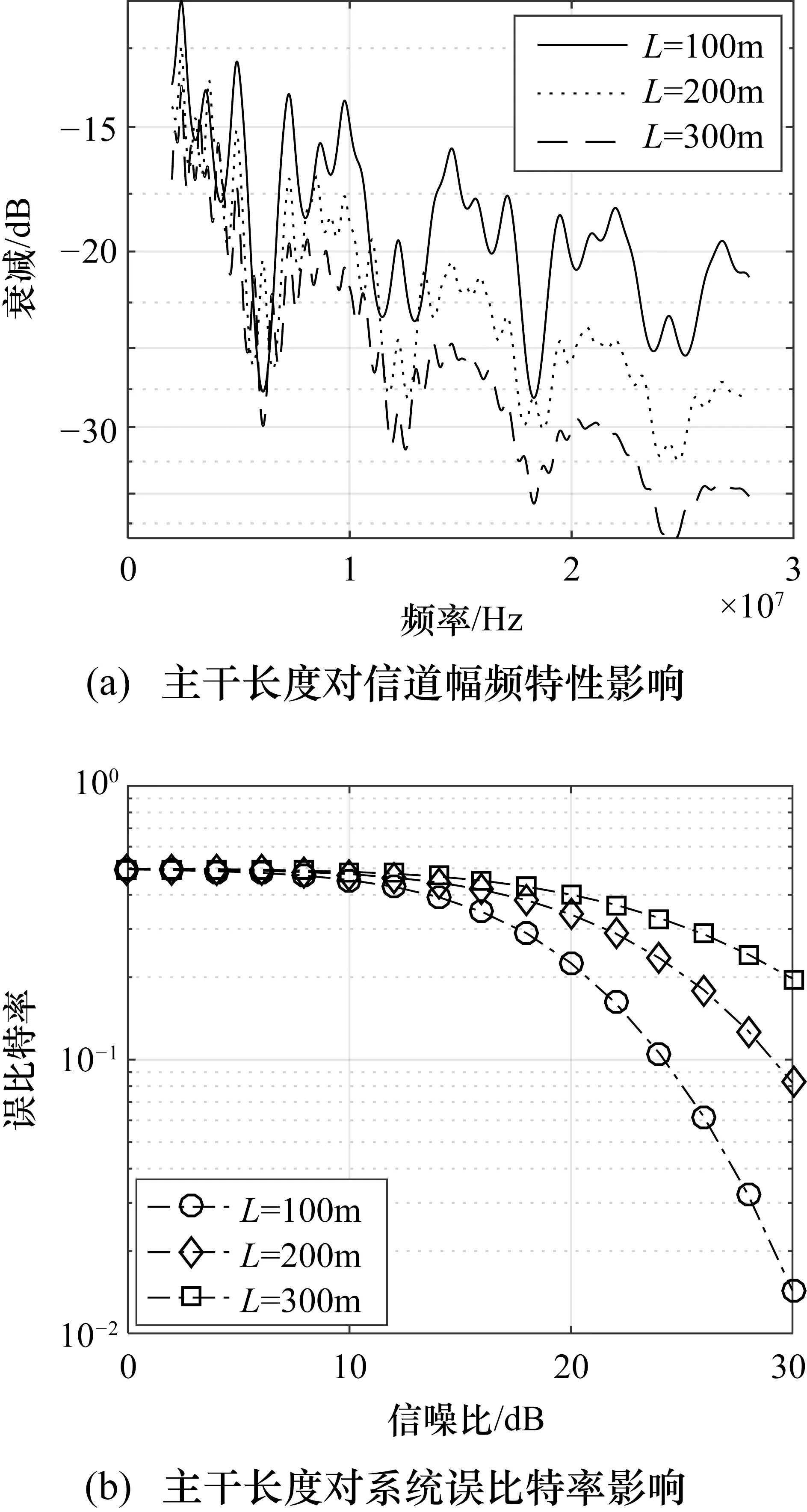
图7 主干长度对系统影响
3.2.2 支路长度影响
发送端到接收端电力线主干长度为200 m,支路负载为50 Ω,分支节点位于主干线路中心。分析支路长度分别为10 m,20 m,30 m时对系统的影响,如图8所示。
图8(a)为不同支路长度下信道幅频特性,当支路长度增加式,陷波频点的数目变多,但衰减趋势类似;图8(b)为支路长度对系统误比特率的影响,图中支路长度的变化对系统误比特率影响不明显。
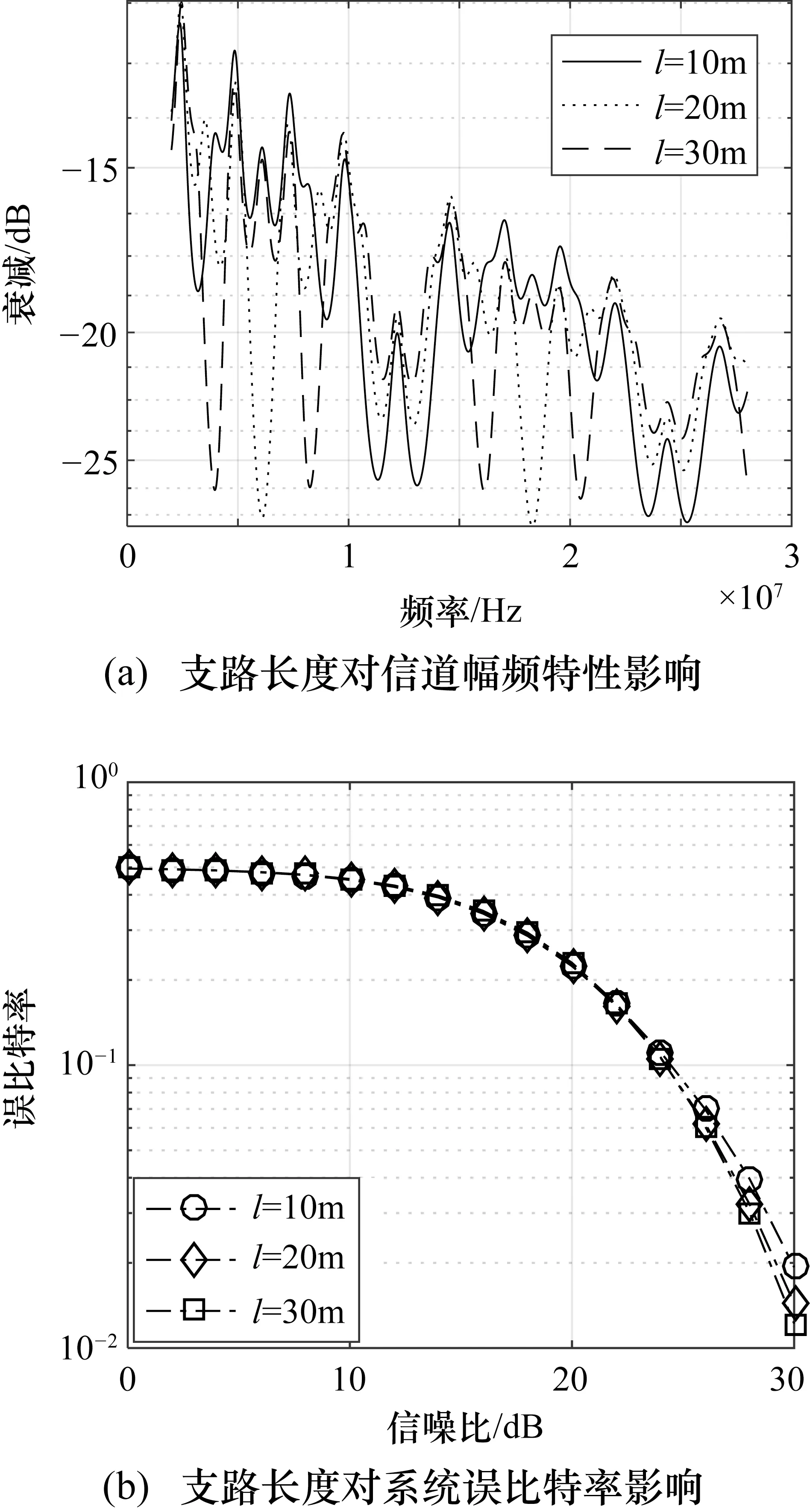
图8 支路长度对系统影响
3.2.3 支路负载影响
由于低压电力线插座上连接的电器多种多样,其负载类型与大小也不尽相同。本节讨论不同的负载特性对系统的影响,电力线主干长度为100 m,支路长度为20 m。
首先考虑纯阻性负载的影响,取支路负载分别为50 Ω,100 Ω,200 Ω,信道衰减如图9(a)所示。前文中采用电力线的特征阻抗为234 Ω,图中支路负载等于50 Ω时,陷波频点衰减值最大,当阻抗增加时,信道衰减幅值慢慢减小,支路的负载阻抗等于200 Ω时,陷波频点几乎不见。图9(b)中显示不同负载对系统误比特率的影响。随着支路负载阻值接近线路特征阻抗,系统性能变好,误比特率逐渐降低。电力线支路为感性负载时,在高频信号下相当于开路,其信道幅频特性及系统误比特率与纯阻抗下阻值较高时一致[18-19]。

图9 支路负载对系统影响
4 结束语
本文介绍了基于OFDM的低压宽带电力线通信系统模型,并利用TL理论和Middleton A类噪声建立信道传输函数和噪声模型。
通过仿真分析电力线网络参数和噪声参数对信号传输的影响可知:① 在信道噪声特性中,噪声总功率确定,当改变参数使米特尔顿A类噪声模型接近高斯噪声时,系统误比特率增加,性能变差。② 在信道网络结构中,随着电力线主干长度的增加,陷波频点位置不变而衰减逐渐变大,系统通信性能变差;支路长度改变会影响陷波频点的个数,但其衰减趋势不变;纯阻性支路负载,对系统的影响与信道特征阻抗的匹配度有关;支路负载为感性时,高频下支路等效于开路。研究了可变参数对信道衰减和通信系统的影响,为将来低压宽带PLC系统的搭建提供了一定的理论基础。
