基于谱峰斜率进行变步长搜索的DOA估计方法

樊文倩，李 舰

(西北大学 信息科技与技术学院，陕西 西安 710127)

波达方向(Direction of Arrival,DOA)估计[1-2]是对传感器阵列接收的数据进行分析处理，估计目标的方位或俯仰信息，是雷达、声纳、无线通信等领域的关键技术[3-4]。作为高分辨DOA估计的经典方法，Capon算法[5-6]通过固定步长的谱峰进行穷尽搜索，获得目标的角度信息[5-7]。该方法存在计算量和存储量庞大、运行时间长、实时性差的问题[8-9]。通常情况下，固定步长[10-11]难以协调计算量和收敛速度之间的内在矛盾。大步长可以简化计算复杂度，但难以获得高的估计精度，小步长增加了计算负担，却有利于提高分辨性能。变步长算法通常包含大步长的粗搜索和小步长的精搜索过程，可较好地平衡收敛速度和估计精度。

文献[12]深入研究了变步长理论，在低信噪比的微弱信号和大误差复杂场景下，提出一种改进的变步长最小均方算法，提出了步长因子和误差之间的函数关系，使步长因子对时变系统具备跟踪能力，该自适应算法对干扰滤除效果十分显著。文献[13]提出一种分级迭代变步长算法，很好地解决了收敛速度与稳态误差之间的矛盾，该算法对盲源分离具有更稳更快的分离速度和稳态性能。

本文提出了一种低复杂度、变步长的搜索算法，首次搜索使用大步长的Capon算法进行搜索，根据谱峰首次搜索结果确定DOA检测范围，并求出该范围内的斜率值，根据斜率值首次小于零确定谱峰在其左侧，记斜率小于零点为P，所以取该斜率对应范围的左值，同时向左取P-2点，并从P-2点处开始向右进行变步长搜索，根据上一步的步长x=1，选取步长函数进行变步长的迭代逼近搜索，并计算每个步长对应的谱峰函数的斜率值Ki，直到斜率值首次小于零，并取斜率值小于零的区间的左值，作为本次期望信号的估计角度DOA。

1 数据模型及Capon算法

空间中L个窄带信号，同时入射到M个半波长的均匀线性阵列，阵元间d=λ/2，P个远场窄带信号以λ为波长入射到阵列，设各通道独立且附加加性高斯白噪声(AWGN)，定义DOA为信号来向与阵列法线的夹角θ，以第一个阵元为参考点，在第t次快拍下阵元m(m=1,2,…,M)接收的P个信源的总响应表示为

(1)

式中,Sp为第P个信源的复包络；nm为第m个阵元上的噪声，则阵列一次快拍的接收数据也可表示为

x(t)=A(θ)S(t)+n(t)

(2)

式中，x(t)为M×I维的接收数据向量；S(t)为L×I维的信号向量；n(t)为M×I维的加性高斯白噪声向量；A(θ)为M×L维导向矢量矩阵，导向矢量a(θl)定义为

a(θl)=[ejx1wl,ejx2wl,ejx3wl,…,ejxMwl]T

(3)

式中，ωl=2πsinθl/λ为第l个阵元接收信号的角频率；λ为信号的中心波长；xi(i=1,2,…,M)为第i个阵元的坐标，阵列输出的协方差矩阵表示为

(4)

(5)

式中，a(φ)为期望信号的方向；R-1为R矩阵的逆矩阵。

2 本文提出的算法

假设空间有L个窄带信号，同时入射到M个半波长的均匀线性阵列，阵元间d=λ/2，P个远场窄带信号以θ=[θ1,θ2,…,θp]入射到阵列，入射波长为λ，设各通道独立且附加的噪声是加性高斯白噪声，定义DOA为信号来向与阵列法线的夹角θ。经典Capon超分辨DOA估计方法采用固定步长进行谱峰穷尽搜索，存在计算量和存储量庞大、运行时间长、精准度不高的问题。

所提算法的具体实现步骤如下。

① 利用经典的Capon算法，先使用大步长的均匀搜索方法，根据Capon算法的谱峰公式[9]

粗略地估计出谱峰值的范围，并截取该范围，利用斜率公式

求出截取范围内的谱峰斜率值Ki。式中，jdpf(i+1)为第i+1个点的角度谱峰值；jdpf(i)为第i个点的角度谱峰值。

② 根据上一步求得斜率值，找出截取范围内斜率首次小于零对应区间的左值P，由于谱峰值在P点左侧，所以向左取值P-2，并从P-2处开始向右进行变步长搜索。

3 仿真分析

3.1 仿真条件

本文的所有仿真实验均是在装有Inter®CoreTM2 Duo CPU E8400@3.00 GHz和6.00 GB的RAM，MatlabR2018ade PC机上实现的，本文提出的算法属于初期的理论阶段，因此所有的数据均采用理想的、假设的数据来进行验证。

在Matlab中进行大量的仿真实验，分别从RMSE、算法复杂度和分辨成功率这3个方面对所提算法进行性能评价。假设阵列天线为18阵元的均匀线性阵列，阵元间距为半波长，期望信号的来波方向是36.7°。均匀线阵所加载的误差均值为零，方差为正态分布的随机值，并且每个阵元的误差单独加载，针对每种变量进行试验，每次采用100次Monte Carlo独立实验的平均结果，将其均方根误差作为评估阵列数据处理误差对算法性能影响的依据。

3.2 改进算法的仿真实验

在仿真实验中，假设有18个均匀线性排列的阵元，阵元间距为λ/2，信号之间相互独立，信噪比为-6，期望信号的来波方向为36.7°。

第1步：用bc表示步长，取bc=5，采用经典的Capon算法在[1°,90°]间进行谱峰粗搜索，仿真结果如图1所示，得到粗略的谱峰范围为[30°,40°]，截取谱峰范围[30°,40°]，并求出该范围内每个点对应的斜率值，仿真结果如图2所示。

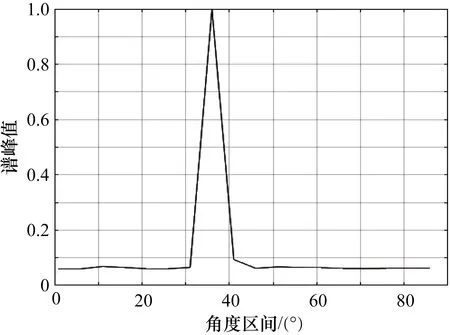
图1 步长为5 的谱峰粗搜索

图2 31°～41°间谱峰斜率值

第2步：根据斜率值首次小于零的左侧为谱峰的特点，找到斜率值首次小于零的区间的左值37，同时再向左取值35,并从点35处开始向右进行变步长的谱峰搜索。

图3 算法流程图

3.3 RMSE的仿真结果

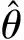
(6)

图4～图6是两种算法在改变信噪比、阵元数和快拍数的情况下的RMSE性能的实验仿真图。由仿真图4～图6可得，在信噪比、阵元数和快拍数改变的情况下，所提算法的RMSE更小，更接近期望信号角度。

图4 不同信噪比对RMSE的影响

图5 不同阵元数对RMSE的影响

图6 不同快拍数对RMSE的影响

3.4 算法的复杂度

通过算法复杂度分析本文所提算法性能，首先提出两个关于衡量算法复杂度的性能指标：① 时间复杂度，指执行算法所需要的运行时间[15]；② 运算复杂度，指程序里所包含的加减乘除、转置及求正弦等次数的和。本次实验通过比较所提算法和Capon算法的运行时间和RMSE来衡量两种算法的复杂度。实验结果如表1和表2所示。

从表1、表2中得知，在一定条件下，所提算法在运行时间上并没有节省，而精度平均值是取10次RMSE的平均值来衡量的，因此在精度的准确性上精确了近9倍，计算过程如下：

表1 两种算法运行10次的RMSE 单位：(°)

表2 两种算法RMSE的平均值和运行时间

本文所提算法的最大贡献就是准确度的提高，通过比较两个算法的RMSE来进行衡量，传统的Capon算法的平均RMSE为0.7588°，而本文提出通过引入步长函数，进行变步长的谱峰值搜索的方法求得的RMSE为0.0870°，所以相对原有的算法，本文所提算法在精度的准确性上精准了近9倍。而精度是通过比较两个算法多次运行的RMSE来进行比较的。传统的Capon算法的一次运行时间为130.5 s，而本文提出的方法进行谱峰搜索时一次运行时间为247.2 s，所以相对原有的算法本文所提算法在运行时间上并没有节省，这也是所提算法的一个不足之处。

3.5 分辨成功率的仿真结果

分辨成功率(Probability of Resolution,PR)即在一定条件下，取一个误差阈值，统计小于这个阈值的次数与总共实验的次数的比例。设所允许的角度估计误差门限值为▽θ，由于本次的实验的期望角度为36.7°，精确到了小数点后一位，所以取▽θ=0.5，仿真结果如图7所示，在Q次独立实验中N个DOA角度的估计值均满足式(7)的实验次数为Q1次，则PR=(Q1/Q)，仿真结果如图7所示。

图7 误差门限为0.5时的PR

(7)

当估计的角度为两个且两角度相距很近，分别为θ1和θ2且谱峰函数f(·)取值满足式(8)，即认为θ1

和θ2分辨成功。同理存在多个信号时，且角度间相距很近时，记为θi(i=1,2,…,n)。

(8)

(9)

通过仿真图7可得，估计一个角度时，所提算法的PR明显优于传统的Capon算法，当存在多个信号时，可以采用上述式(9)的方法。

4 结束语

本文所提算法采取简单的方法快速估计出期望信号的角度，在准确度上相比传统的Capon算法精准了近9倍，改善了定位的准确性，避免了穷尽的谱峰搜索。仿真实验表明：在相同信噪比下，所提算法的分辨成功率更高；同时所提算法的RMSE在信噪比、快拍数和阵元数变化的情况下，均明显优于经典的Capon算法，估计精度优于传统的Capon算法，更接近于期望信号。

虽然本文所提算法检测单次算法运行时间上高于传统的Capon算法，但是降低了算法的估计误差，减少了无效的谱峰搜索。因此本文所提算法通过引入步长函数，进行变步长迭代逼近搜索求斜率值的方法，求解出期望信号的DOA，避免了穷尽的谱峰搜索，更高效准确地估计出期望信号的DOA。