小波包变换在火箭发动机脉动压力分析中的应用

杨 懿, 郭亚男, 王永鹏, 陈文丽, 贾志杰, 吕守国

(北京航天试验技术研究所，北京 100074)

在火箭发动机试验中，脉动压力一般用于测量推力室内高频、高压、高温压力，具有测量精度高、系统频响快、测量范围大等多种特点。不仅能弥补稳态压力无法满足高、低温和水击压力等特殊环境下测量能力的不足，还能为考核发动机性能、评估燃烧状态等提供重要的参考依据。

目前，对于脉动压力数据的分析尚停留于简单观测其在时域中的幅值大小。较稳态压力参数而言，脉动压力参数的数据采样率更高、测量手段更先进、测量精度更高、系统响应频率更快。因此，对于脉动压力数据的分析不仅要在时域内精确分析压力概值，还需要深度挖掘数据在频域内的其他信息，并通过与其他测量参数数据相结合的手段，为设计部门准确评估发动机燃烧状态和动态性能提供准确可靠的依据。

在数据时频分析领域，常用的方法有快速傅里叶变换(FFT)、小波分析、小波包变换等方法，这些方法各有特点。傅里叶变换建立了时间域和频率域相互转换的关系。通过选择不同的窗函数，可以清晰地分析数据在全频域的特征。但该方法以正弦波及其高次谐波为标准基，不能分析局部频率[1]，无法分析数据在某个时域内的特征。与傅里叶变换相比，小波分析能够实现时间频率的局部化分析，通过伸缩平移运算对信号逐步进行多尺度细化分析，最终达到在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率[2]。小波包分析是小波分析理论的改进型算法。在小波包数据分析和故障定位的研究领域，诸多研究人员都取得了相应的成果。商霖等[3]通过研究固体火箭燃烧室内脉动压力能量分布的频率特性与随机振动的关系，研究发动机的工作原理。郭伟超等[4]利用小波包多分辨、分析信号能力强的优点，采用小波包能量谱与主成分分析相结合的方法提取振动信号中的故障特征信息，精确定位轴承的故障类型。王二化等[5]以多传感振动信号为研究对象，将小波包各个频段的能量比系数作为齿轮裂纹的故障特征，通过神经网络模型特征分类法能有效辨识不同工况下的齿轮故障。

本文采用小波包变换分析方法对火箭发动机燃烧室脉动压力数据进行去噪和树状分解分频段分析，结合对应振动测点的数据，分析燃烧室脉动压力与振动能量在频域内的共性关系。结果证明该方法取得了较好的效果，并对后续其他相关产品试验中脉动数据分析具有重要的应用价值。

1 脉动压力测量系统的组成及数据特征

火箭发动机试验中，脉动压力测量系统一般由脉动压力传感器、传感器循环冷却系统、供电电源、信号转换装置和数据采集系统组成。测量系统组成图如图1所示。

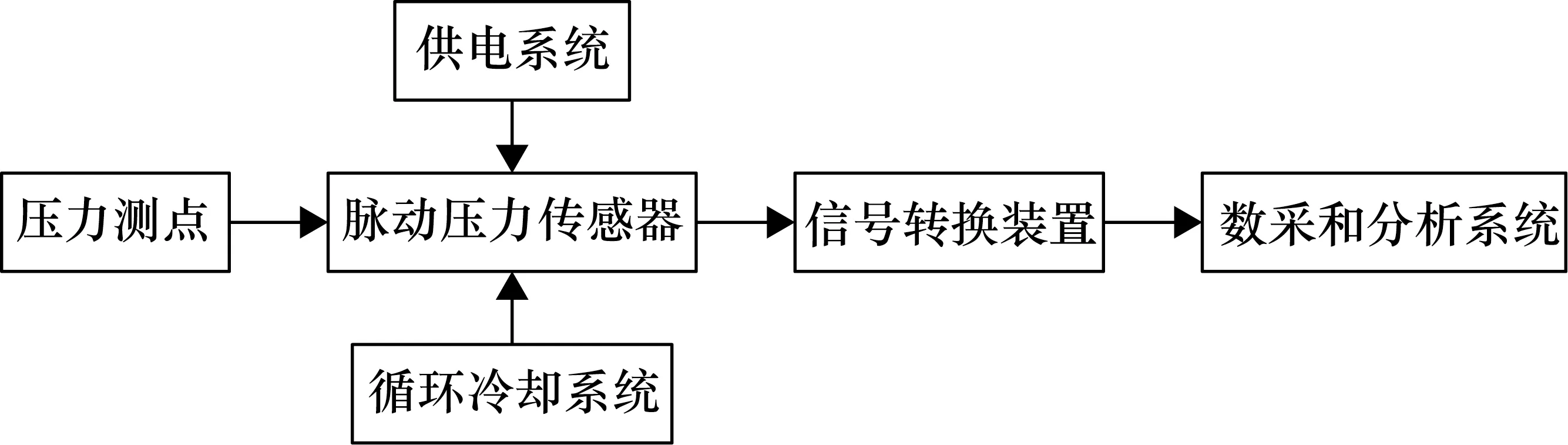
图1 脉动压力测量系统组成图

脉动压力参数的测量需要精确体现燃烧室高温、高压、剧烈振动环境下的压力变化信息。对硬件的要求主要体现在以下3个方面。

① 测量系统的频率响应快，通常在10 kHz以上。

② 传感器耐高温、高压和剧烈振动，频率特性至少应有10～20 kHz的平坦段。

③ 采集系统的采样频率高，为捕捉瞬时压力变化信息，采样系统一般具备10 kHz/s以上的高采样速率。

因此，对硬件系统的高要求决定了脉动压力参数数据具有高频、采样点多和数据容量大等显著特征。

2 小波包变换的基本原理

小波包分析方法具备小波分析多分辨分析的优点，能够在全频域内将信号频带划分为多个层次，根据被分析信号的特征自适应地选择相应的分析频带，使其对信号的频谱分析更加合理。因此，与小波分析相比，小波包分析方法对时频分析的能力更强，对信号的描述更加细致。在消除信号和图像噪声、提取特征信号、信号压缩等领域应用更加广泛。

2.1 小波包理论的基本原理

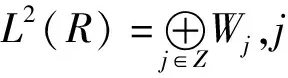
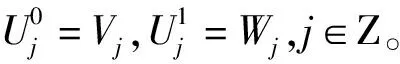
(1)

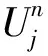
(2)

(3)

式中，g(k)=(-1)kh(1-k)，两系数具有正交关系。尺度函数φ(t)与小波函数ψ(t)满足式(4)、式(5)的双尺度方程[6]：

(4)

(5)

由式(1)和式(2)构造序列{un(t)}n∈Z，n为非负整数，则称该序列{un(t)}n∈Z为由基函数u0(t)=φ(t)确定的正交小波包。

令{un(t)}n∈Z是关于hk的小波包族，令n=0，1，2，…，j=0，1，2，…，并对式(1)进行迭代分解，则有：

(6)

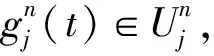
(7)

小波包分解算法如下[6]：

(8)

(9)

小波包重构算法如下[6]：

(10)

(11)

通过以上分析可以看出，相对于小波变换在高频分析能力上的不足，小波包变换能够在全频域中对信号进行分解，描述信号特征的能力更强。

在信号多层分解过程中，通常采用小波包Wicherhauser树状分解法对信号进行分解，然后再对处理后的分解信号进行重构。以3层小波包树状分解为例，其分解过程如图2所示。

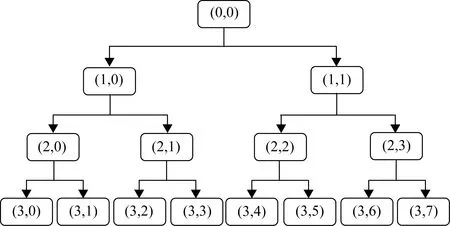
图2 Wicherhauser树状分解流程图

由上述分析可以看出，小波包分解的实质是对信号分解中的各级均进行高通和低通滤波。通过高、低通滤波器组将信号分解到不同的频段内。

2.2 小波包最佳基波的选取

为方便对信号进行时频分析，需要选择合适的基波函数，将基波函数中的信号提取出来。对应图2中的多层分解。自j=0向下分解的过程中，每一层均包含了多个基波。需要从中选择最佳的基波。基波的选择关系到信号分解以及时频分析质量的好坏。

工程应用中常用信息代价函数来描述类似的选取程序过程。通常有3种信息代价函数：Shannon信息熵法、阈值法和P范数法[7～10]。其中，Shannon信息熵法比较适用于非平稳信号的分析，也是本文研究所选用的方法。

信息代价函数通过表征信号的有序程度和数值计算实现对信号有序性的测试。基本定义如下。

(12)

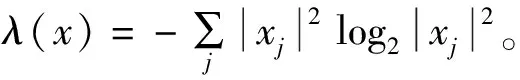
Shannon信息熵用λ(x)可表示为[6]

H(x)=λ(x)/‖x‖2+log2‖x‖2

(13)

2.3 小波基函数的选取

在工程应用中，常用的小波基函数有：Haar函数、DBN函数和SymN函数等。各基函数都有自身的特点。在信号处理中使用的基函数不同，得到的处理结果也不一样。在实际的运用过程中需要根据数据和小波基函数自身的特点，选择合适的小波基函数[5]。

小波基函数的选取主要遵循以下3点原则[11]。

① 支撑长度。支撑长度是指尺度函数、小波函数及其傅里叶变换的收敛速度。

② 对称性。对称性能够有效避免信号处理中的移相问题。

③ 正则性和消失矩。正则性和消失矩呈正相关关系，决定小波系数重构的稳定性。

各种小波基函数的特点如表1所示。

表1 各小波基函数特点

Haar函数从Shannon正交尺度函数演化而来，以矩形函数作为标准正交基得出时域标准正交尺度函数，按照多分辨逼近原则推导Haar正交小波函数。根据其理论基础[8]，Haar函数在时域中的支撑长度很短，时域分析能力强，但是衰减速度慢，在频域中的局部分析能力较差。仅仅有一阶消失矩，光滑程度低，表现力差。不适合分析波动强、采用频率高的脉动压力数据。

DBN函数是一类紧支集正交小波，N为有界正整数。该函数以周期函数为基础，同时具备高、低通滤波器的特征。随着N增大，衰减性降低，光滑性增加，消失矩亦随之增高[8]。但总的来说，该函数光滑性不好。

SymN函数是DBN函数的改进型，除了具备DBN函数的优点之外，其对称性比DBN函数要好，能够有效降低在对信号进行分解、重构时的相位失真问题[12]。

在工程应用中，为获得较好的去噪效果，通常需要根据数据和小波基函数的特点，选择小波系中对称性和正则性好的小波基函数往往能够取得较好的去噪效果[13]。以本文试验中的脉动压力数据为例，试验第10.910～第10.920 s如图3所示。

图3 试验中第10.910～10.920 s脉动压力数据

根据图3中的脉动压力波动特征可以看出，由于采样率高，数据在一定范围内波动剧烈，但对称性好，具有相对稳定的周期，曲线光滑。基于前文3种小波基函数和脉动压力数据的特征分析，本文选择SymN函数进行数据的去噪处理。

2.4 小波包去噪的基本步骤

在工程应用中，不同的信号中所包含噪声分量的比重有高有低，一般采用阈值法，通过设定不同的阈值对含噪信号进行去噪处理。小波包阈值去噪法一般分为以下4个步骤。

① 确定最优小波包基。

② 信号分解。

③ 设定小波包分解系数的阈值。对于每一个小波包分解系数，选择合适的阈值。

④ 信号小波包重构。根据小波包分解特征信息和系数进行小波包重构。

工程应用中通常将信噪比、相关系数、均方根误差作为去噪效果的评价指标。其中信噪比和相关系数是两个最重要的指标。信噪比是信号功率与噪声功率的比值，比值越大说明去噪的效果越好。相关系数是指去噪后的信号与原始信号特征信息的相似程度。本文选定信噪比作为小波包分解去噪效果的评判指标。

3 脉动压力数据分析实例

3.1 数据分析的基本步骤

根据第2节的论述和多位技术人员的研究内容[14-16]，采用小波包变换对液体火箭发动机试验脉动压力数据进行分析主要分为以下步骤。

① 采用小波包分解对原始数据进行去噪处理。选定合适小波基、分解层数、阈值等。

② 选定合适的小波包基波。根据Shannon信息熵标准选定合适的基波。

③ 选定小波基函数类型和分解层数。

④ 信号的小波包分解、重构。

⑤ 分析各高、低频系数的特征。

⑥ 数据验证。根据分析结果，结合其他测量参数和分析方法对小波包变换的结果进行验证，提取特征信息。

上述分析均通过Matlab软件编程实现。

3.2 数据分析

某次火箭发动机试验脉动压力数据采集系统采样率为10 kHz/s，燃烧室脉动压力测点名称：Pcios1。数据全程和局部数据分别如图4、图5所示。选取第10.80～11.00 s共计2000个样本点作为分析数据。

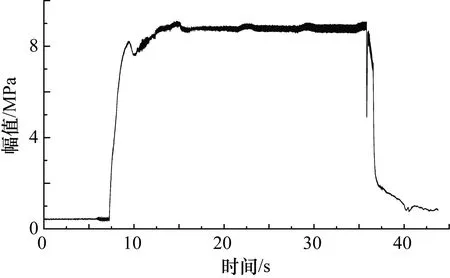
图4 全程脉动压力数据图

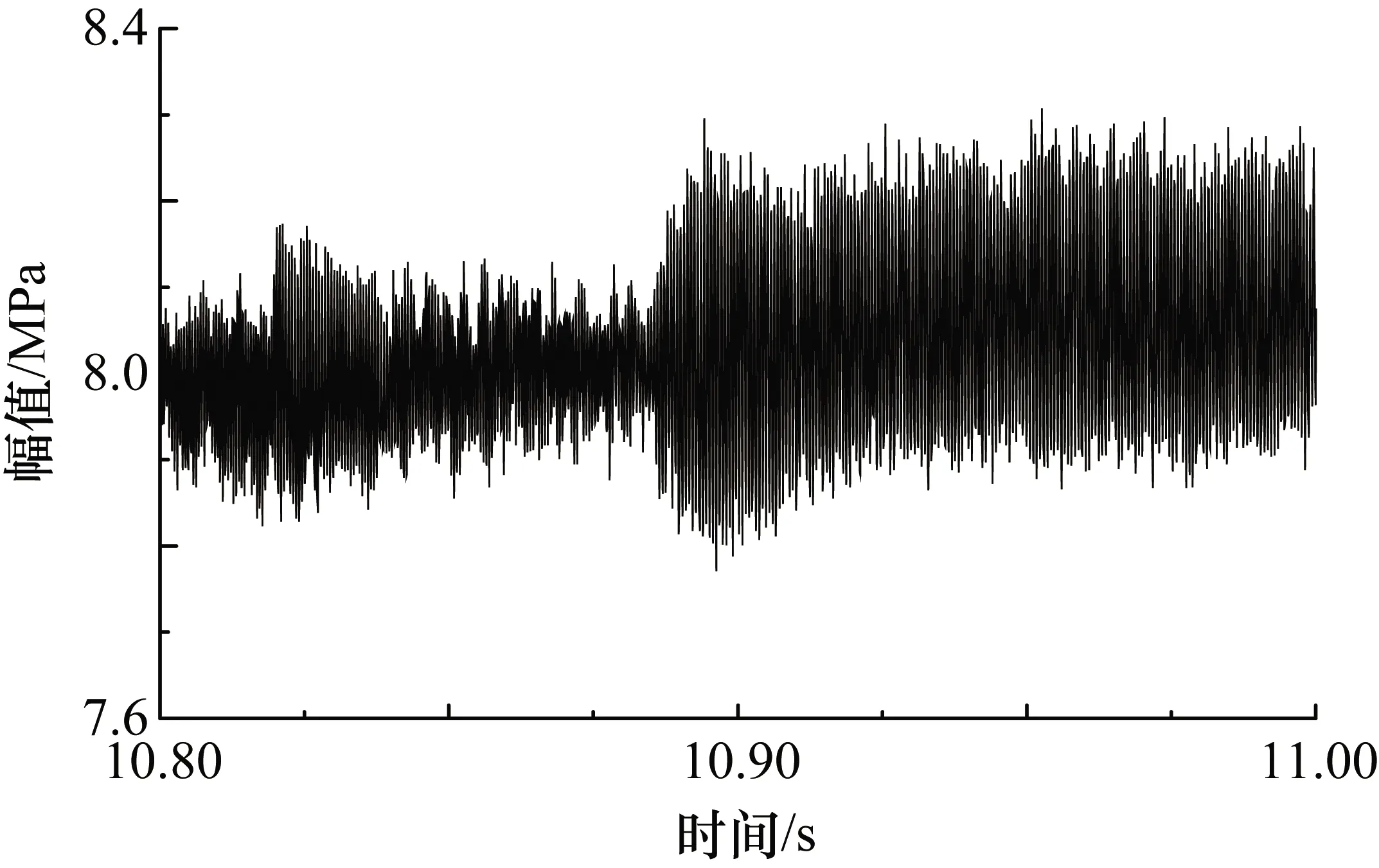
图5 局部脉动压力数据图

3.2.1 传统的数据分析方法

传统的数据分析方法中，对于脉动压力数据的分析主要考察其在时域内的特征信息。在发动机试验过程中，根据发动机的工况，一般分为启动段、稳定段和关机段。分别考核上述3个工况的压力概值。详细数据如表2所示。

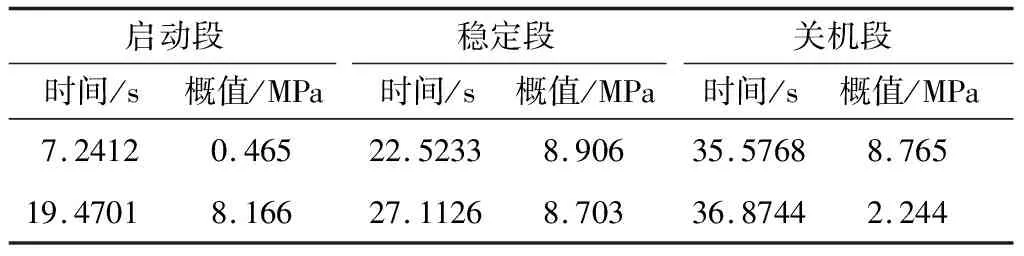
表2 发动机不同试验工况下脉动压力数据

从表2中的数据可以看到，传统的数据分析非常清晰地定位燃烧室在试验各工况下的压力概值，也为准确评估燃烧室的燃烧状态提供了可靠的数据依据。但是不能获取发动机不同工况下脉动压力在频域下的特征信息，无法为研究发动机动态性能提供可供参考的依据。

3.2.2 小波包变换分析方法

根据表1中各种小波基函数的特点，选定Sym3小波，自选阈值法(阈值thr=9.4712)，分解层数分别为2～4层，原始数据进行去噪处理结果如图6所示。3种去噪方法的信噪比如表3所示。

图6 Sym3小波、自选阈值、2～4层分解去噪效果图

表3 Sym3小波、自选阈值、2～4层分解去噪结果信噪比数据

结合图6和表3的数据可以看出，Sym3小波在保持信号原有趋势信息的前提下，能够较好地消除脉动压力信号中的噪声信息。随着分解层数的增加，信噪比呈下降的趋势，去噪后的曲线也越光滑，表明在消除噪声的同时也过多地消除了原始信号中的有用信息。综合上述信息，为尽量保存原信号中的有用信息，在消除噪声的分析环节选择2层分解去噪。

为验证小波去噪结果是否正确，以发动机燃烧室脉动压力测点Pcios1附近两个稳态压力测点Pcio1和Pcio2的平均压力值作为参考标准，以200个样本为间隔，计算样本点中200～2000点的数据在去噪前、后与稳态压力平均值之间的相对误差。以200，400和600点的数据为例，计算结果如表4所示。

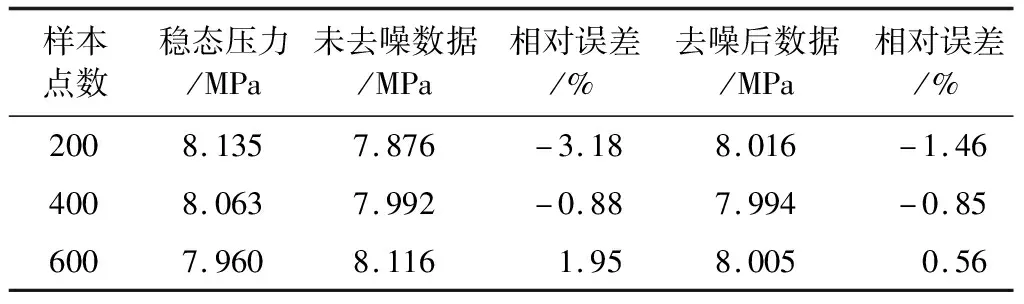
表4 Wicherhauser树状分解频带信息

从表4中相对误差的计算结果可以看出，采用小波去噪后，数据的相对误差较未去噪数据均得到了有效的降低。对于800～2000样本点的相对误差分析也能得到相同的结果。

采用Shannon信息熵标准、3层分解、DB5小波基波对信号进行分解。根据Wicherhauser树状分解重构算法，在第3层分解中将脉动压力数据采样频率(10 kHz)分成8个频率段，分解层对应频率段如表5所示。DB5小波基波3层分解Wicherhauser树状图和(2，1)节点的系数图如图7所示。(3，0)～(3，7)节点的高、低频系数图如图8所示。

图7 Wicherhauser树状图和(2，1)节点的系数图

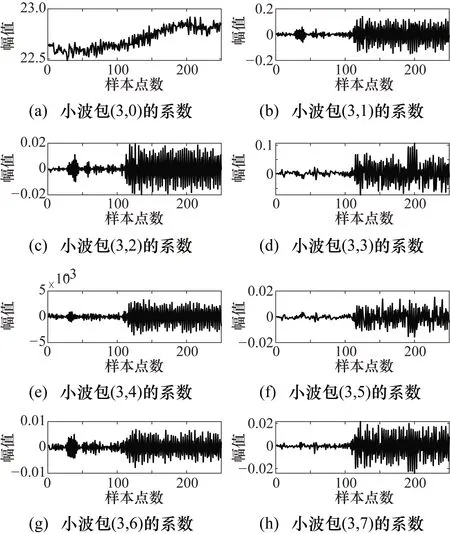
图8 (3，0)～(3，7)节点的高、低频系数图

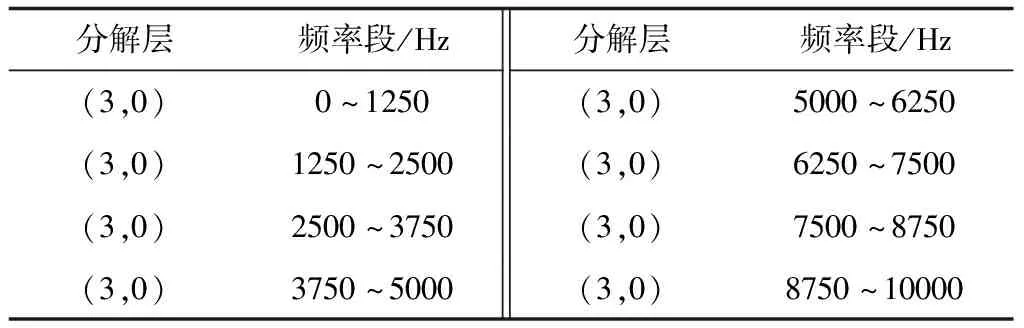
表5 Wicherhauser树状分解频带信息

从图8中可以分析得出，与节点(3，1)～(3，7)相比，节点(3，0)系数对应的幅值较大。节点(3，0)对应的是0～1250 Hz的中低频段，说明在中低频率段，脉动压力所包含的能量较大。从图5中第10.80～11.00 s脉动压力数据趋势分析，燃烧室内脉动压力幅值大致在7.35～8.35 MPa范围内波动且呈现周期性的压强振荡特征，且压力的振幅呈递增趋势。说明在该试车时间段内随着推进剂燃烧对压强振荡响应，燃烧产生的能量持续注入燃烧室工作系统，引起脉动压力剧烈振荡。其影响在燃烧室振动测点数据中应该能够得到体现。为验证小波包分解的有效性和准确性，分别对脉动压力测点(Pcios1)、燃烧室轴向(a1)、径向(a2)和切向(a3)振动测点进行FFT频谱分析，分析结果分别如图9～图12所示。

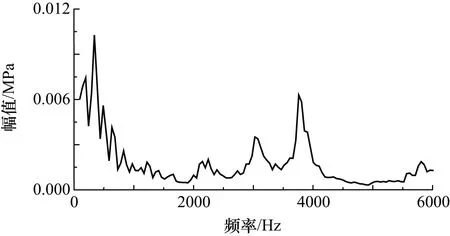
图9 脉动压力测点(Pcios1)频谱分析图

图10 振动测点(a1)频谱分析图

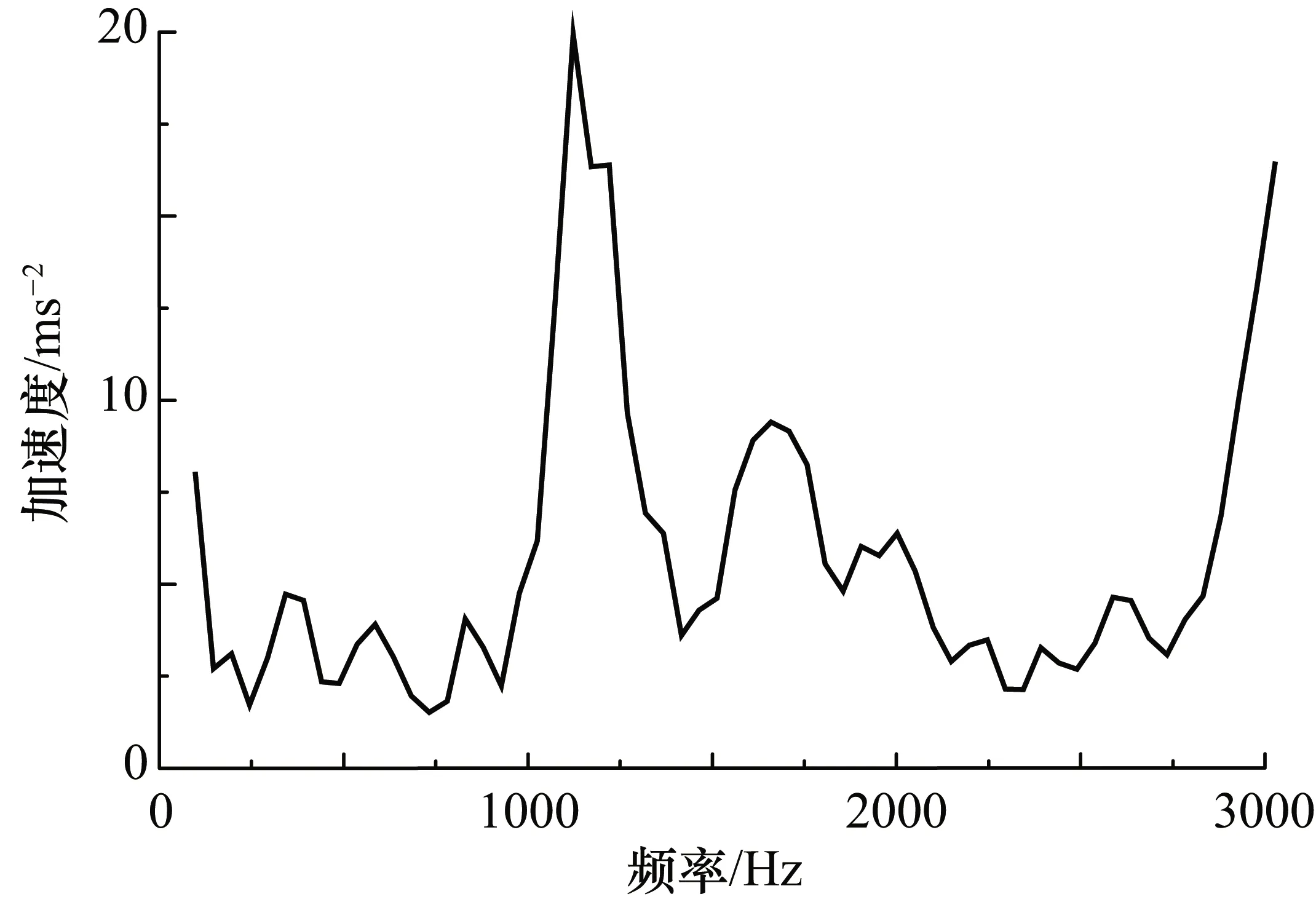
图11 振动测点(a2)频谱分析图

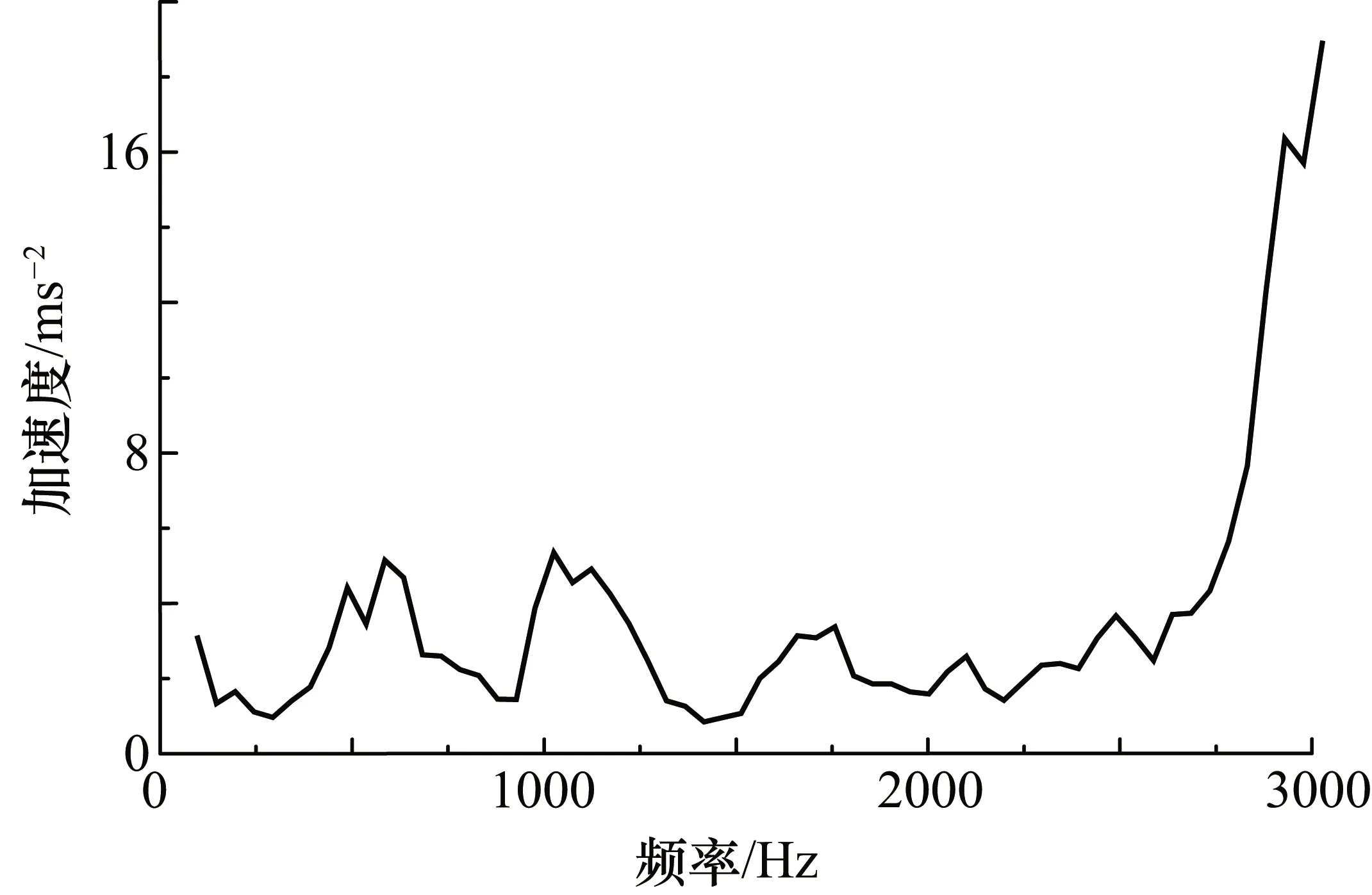
图12 振动测点(a3)频谱分析图

从图9中可以看到，0～1250 Hz的中低频段存在多个振荡波动的幅值尖峰，表明在该频率段，燃烧室内存在剧烈的压力振荡。从图10～图12中可以看出，径向(a2)和切向(a3)振动测点同样在0～1250 Hz的中低频段存在多个加速度幅值尖峰，表明在该频率段燃烧室存在径向和切向的振动剧烈。而轴向(a1)振动测点在该频率段内曲线较平缓，无加速度幅值尖峰，表明在该方向的振动较小。

由上述验证分析结果可见，小波包对脉动压力数据分析与振动测点频谱分析结果相吻合。

4 结束语

通过对脉动压力数据特征分析，利用小波包变换多分辨分析、全频域自适应分解信号的优势，采用小波包自选阈值去噪、小波包Wicherhauser树状重构算法、Shannon信息熵基波选择标准等方法对脉动压力数据进行细致、准确的频域分段分析与特征提取。通过与稳态参数对比分析论证了选择合适的小波基函数对数据进行去噪后的误差。通过与传统的脉动压力数据分析方法的对比，论证了小波包分解在验证数据变化规律、分析特征频率段内能量分布有着传统分析方法不具备的优势。数据分析的结果展现了脉动压力数据在频段内的系数特征和能量分布情况，并通过对脉动压力数据和相应振动测点数据的频谱分析，验证了小波包分解结果的符合发动机实际运行工况。该方法在其他型号发动机和组合件试验脉动压力数据分析中有重要的应用和推广价值。