基于测试成本元素的众包测试缺陷数量估计模型

姚 奕，刘语婵，杨 帆

(陆军工程大学 指挥控制工程学院，江苏 南京 210007)

随着互联网群智技术的深入研究，测试中人员多样性和互补性带来的缺陷发现效率的提高，使得众包测试得到了飞速发展[1]。现有众包测试平台发布测试任务后，项目经理通常只根据他们的个人经验来计划众包测试任务的结束。例如，他们通常采用基于时间或基于参与者的条件来结束众测试任务。然而做出合理的决定是很有挑战性的，众包测试通常被视为一个黑箱过程，管理者的决策仍然对其实际进展不敏感，这些基于经验的决定可能会导致无效的众测过程。这表明了改进当前众包测试实践的实际需要和潜在机会。因此，众包测试平台希望寻找能够实时预测或估计软件缺陷数量和可靠性的软件可靠性建模技术。通过比较预测和检测的缺陷数量以及评估软件测试后的可靠性，以评估测试任务的进度，能够合理判定任务结束，避免浪费大量的测试时间和资源。

关于众包测试缺陷数量预测的研究很少，Wang等[2]从软件的可靠性出发对测试任务完成度进行评估。Wang首先根据测试报告中缺陷的重叠性利用捕获-重捕模型预测软件中的缺陷规模，然后通过分析已检测缺陷数量所占缺陷规模的百分比来衡量软件的可靠性。然而，众包测试区别于传统的测试手段，以其参与者的随机多样性与测试报告数量的庞大性使得软件产品被更加合理充分地测试。参与测试任务的人员越多越活跃，那么平台接收到的测试报告也越多，则缺陷被发现的概率则更大。但是缺陷数量是恒定的，大量的人力和报告成本的投入可能会导致测试的低效益性。因此通过研究测试成本与缺陷发现数量的关系来预测缺陷数量。软件可靠性增长模型(Software Reliability Growth Model,SRGM)[3-4]在度量、预测、保证可靠性上被广泛应用，同时也为最优发布时间抉择等软件开发活动提供重要决策支持。SRGM从软件失效的角度进行可靠性建模，采用以微分方程(组)为主的数学手段建立软件测试过程中的若干个随机参量间的定量函数模型，例如测试时间、累积检测的缺陷数量、测试工作量等参量。基于求解出的累积检测缺陷数量函数表达式，可以获得测试阶段的可靠性[5]。SRGM除了包括完美排错模型[6-8]、不完全排错模型等类型[9-10]，还考虑了测试资源和测试环境，基于测试工作量(Testing-Effort,TE)和变动点(Change-Point,CP)的SRGM相继被提出[11-15]。各种类型的TE开始广泛地出现在SRGM中，使得融入测试资源的花销在建模中成为常态。

基于众包测试人力成本和测试报告成本数量庞大的特点，本文对传统的基于单个TE的SRGM进行了改进，将测试人力和提交的测试报告数量同时纳入测试工作量考虑范围，提出了一种针对众包测试的软件缺陷数量估计模型(Crowdsourced Test Defect Number Estimation Model,CTDNEM)。其中利用相关函数对测试人力和测试报告数量两个测试成本元素进行相关性分析，并基于相关性程度和测试工作量函数(Testing-Effort Function,TEF)建立了一个通用的分段式可靠性建模框架，可以根据不同元素之间的相关性程度来选择合适的微分方程；同时在成本估计中，引入3种TEFs估计测试成本数据，以此选择最优参数代入微分方程求解出测试中累积的检测缺陷数量以及潜在缺陷数量，能够有效提高缺陷数量估计的准确性。

1 传统模型

非齐次泊松过程(Non-Homogeneous Poisson Process,NHPP)类模型由于具有易理解与易使用等优良特性，已成为目前研究最为广泛的一类SRGMs[15]。缺陷的检测与修复是在TE的消耗下进行的，TE可有效地描述软件开发过程中的工作剖面，因而SRGM中应考虑到其存在,本文模型就是在此类模型框架基础上进行改进的。

Zhang等[9]首次针对TE提出了一个相对统一的SRGM框架(Software Reliability Growth Model Based on Testing-Effort,TE-SRGM)，该模型框架的建立基于下面的假设条件。

① 缺陷检测过程随时间服从NHPP过程。

② 在(t,t+Δt)时间内检测到缺陷的平均数量与当前测试工作量消耗率下的软件中剩余的平均缺陷数量成正比。这个比值即为当前的缺陷检测率，它可以是一个常数b，也可以是时间相关的函数b(t)。

③ 每次缺陷被检测出来时，都会立即被完美地修复，而修复只需要很少的时间，且不会引入新的缺陷，因此软件中的缺陷总数是一个常值a。

④ 所有的缺陷都是独立的，并且同样可以检测到。

根据上述假设，即可得到如式(1)所示的考虑TE的NHPP软件可靠性建模框架。

(1)

式中，m(t)为时间间隔[0,t]内的检测缺陷数的期望均值函数；w(t)为测试工作量消耗速率函数，它是测试工作量函数(记为W(t))对测试时间t的导数；b(t)为当时的缺陷检测率；a为软件中的缺陷总数。

在边界条件为m(0)=0，W(0)=0时，将不同形式的测试工作量函数W(t)代入上述微分方程并求解，即可得到各种不同的累积检测缺陷数量函数表达式(记为m(t))。

2 改进模型CTDNEM

针对众包测试人员多样性和测试报告互补性的特点，将测试人力数量和提交测试报告数量作为测试成本元素，并基于TE-SRGM建立了众包测试缺陷数量估计模型CTDNEM，模型的流程如图1所示。

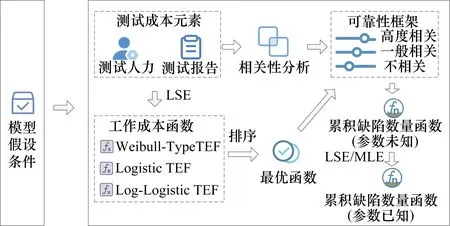
图1 众包测试缺陷数量估计流程

在模型假设的前提下，CTDNEM首先利用相关函数对测试人力和测试报告两个测试成本元素进行相关性分析，其次根据不同元素之间的相关性程度建立了一个通用的分段式可靠性建模框架来对检测过程建模，然后利用实际测试成本数据分别估计3种TEF的参数并进行比较，以此选择出最优的TEF代入微分方程。最终可以估计软件潜在缺陷数量以及各时刻累积检测缺陷数量。

2.1 模型假设

首先，由于众包测试过程只涉及缺陷检测行为，不包含修复工作，该模型需要设置一个虚拟修复过程。本文中此过程属于完美修复，无需结合实际讨论。其次，众包测试软件的规模通常较小，不适用于系统级的分析，因此需要对时间进行细化处理。第三，考虑到测试报告具有高重复率和高互补率的特点，平台需要对报告进行融合，去重等处理。因此CTDNEM对TE-SRGM的假设进行了修改，使其满足众包测试行为的特点。模型需要满足以下假设条件。

① 测试过程中，缺陷检测过程随时间服从NHPP过程。

② 所有的缺陷都是独立的，并且同样可以检测到。

③ 所有测试时间细化，将日历时间转化为时间戳形式，并保证测试起始时间为0。

④ 每次测试报告被提交后，都会进行虚拟修复，即发现的缺陷会立即被完美地修复，且不会引入新的缺陷，因此软件中的缺陷总数是一个常数a。

⑤ 测试报告中重复的缺陷只累积首次发现。缺陷被虚拟修复后，若测试报告中还上报该缺陷，此缺陷将被忽略。

⑥ 在(t,t+Δt)时间内检测到缺陷的平均数量与当前缺陷检测率b(t)及两个测试成本工作量w1(t)和w2(t)的共同作用消耗率下软件中剩余的平均缺陷数量成正比。其中，两个测试成本元素的共同作用情况将在后面讨论。

2.2 测试成本元素

通常SRGM适用于系统级别的缺陷数量估计[5]，而众包测试中待测软件规模较小，TE-SRGM原有测试工作量难以保证模型的准确性。因此基于众包测试特点，可以考虑使用多个测试成本元素，模型将测试人力和提交的测试报告数量纳入考虑范围。

在现实的测试环境中，测试成本元素并不是完全相互独立的，也不是完全一致的，它们或多或少会有一定的联系。因此，模型使用相关系数来表示两个元素的相关性。相关系数最早是由统计学家卡尔·皮尔逊设计的统计指标相关性，其计算公式为

(2)

式中，P为参与的测试人力变量；R为提交的测试报告数量变量；Var代表求方差；E代表求期望值。皮尔逊认为相关系数ρ的绝对值若在0.7以上，就认为P和R有强的相关性；在0.4～0.7之间，可以认为两者有相关性；在0.4以下，则认为两者没有相关性[17]。

本文随机对现有数据集成本数据进行相关性分析，分析结果如图2所示，该数据集的人员成本和报告成本的相关性为0.65，这表明两个测试成本元素之间存在一定的正相关关系。因此，为了提高缺陷数量估计结果的准确性，需要最小化两个因素对彼此的影响。CTDNEM针对不同的相关性程度，建立了一个分段式的可靠性建模框架，可以最小化两个成本元素对彼此的影响。

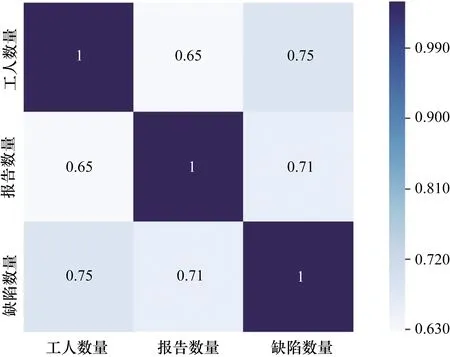
图2 测试人力与测试报告相关性

2.3 通用框架

第一节中TE-SRGM只考虑了单个测试成本元素的情况，无法将两个或多个测试成本元素直接代入式(1)。CTDNEM则提出一个能够包含两个测试成本元素的可靠性建模框架。在式(1)的基础上，模型引入两个测试成本元素来对最终检测到的缺陷平均数量进行计算，考虑到测试成本元素之间的相关性，模型建立如下的可靠性建模框架。

(3)

式中，w1(t)为t时刻测试人员占用率；w2(t)为t时刻测试报告消耗率；a为缺陷总数；λ和μ为相关性调和系数；b(t)为缺陷检测率。

整个测试过程中，总体的缺陷检测率最终都会随着缺陷数量的检测和排除而上升并趋于恒定。因此CTDNEM利用现有的b(t)公式[18]：

(4)

式中，r为弯曲因子,表示软件中不相关缺陷所占的比例。当r=1时，所得到的m(t)即为凹型模型，其余情况得到的是S型模型。

两个测试成本元素的3种相关性情况具体描述如下。

① 当ρ(P,R)≥0.7时，P和R相关性极强。此时两个元素的影响可用其中任一元素代替，微分方程与式(1)相同。

② 当0.4≤ρ(P,R)<0.7时，P和R相关性较弱。此时认定P和R在一定比例上影响缺陷检测数量，在(t,t+Δt)时间内检测到缺陷的平均数量与一定权重下的两个元素消耗率之和成正比。

③ 当ρ(P,R)<0.4时，P和R基本无关。此时认定P和R相互完全独立，共同影响缺陷检测数量，在(t,t+Δt)时间内检测到缺陷的平均数量与两个元素消耗率皆成正比。

3 TEF分析

文献[19]中明确指出，软件中缺陷总数a、缺陷检测率b(t)和测试工作量TE是影响SRGM的重要参数因素。前文已经对前两个因素进行了分析，这里不再赘述。本节将对第3个因素TE进行概要分析。

在软件测试阶段，会消耗大量的测试工作，例如测试报告的数量、测试人力和CPU时间等。消耗的测试工作指示了如何在软件中有效地检测缺陷，因此，资源消耗或人力资源分配可以通过不同的分布进行建模。TE通常用测试工作量函数TEF来表示，即W(t)，下面列出了3个常用的TEFs。

① Weibull-Type TEF：在整个测试阶段，单位时间的TE不为常数。事实上，瞬时TE在测试生命周期中最终会降低，因此累积TE接近一个有限的极限。这种分析是合理的，因为没有软件公司会在软件测试上花费无限的资源。因此，Yamada等提出了威布尔分布，其在(0,t]中消耗的累积TE公式如下[20]：

W(t)=W(1-e(-βtδ))θ,W>0,β>0,δ>0,θ>0

(5)

在测试时刻t消耗的瞬时TE为

(6)

式中，W为TE支出的总额；β为规模参数；δ和θ为形状参数。

Weibull-Type曲线有几种特殊情况：当θ=1，δ=1时，累积TE为指数曲线；当θ=1，δ=2时，累积TE为Rayleigh曲线；当θ=1时，累积TE为Weibull曲线。

② Logistic TEF：当δ>3时，Weibull-Type曲线有明显的峰值现象。这种现象不符合实际的软件开发/测试过程。为此，Huang等提出使用Logistic TE函数来描述测试工作模式。其在(0,t]中消耗的累积TE为[21]

(7)

在测试时刻t消耗的瞬时TE为

(8)

③ Log-Logistic TEF：在某些缺陷数据集中，随着测试的进行，单位TE损耗的速率也可能呈现递增或递减的行为，现有的模型不能捕捉到这种趋势。因此，Gokhale和Trivedi提出了Log-Logistic TE函数，来描述出这种趋势。其在(0,t]中消耗的累积TE为[22]

(9)

在测试时刻t消耗的瞬时TE为

(10)

4 实验验证

4.1 实验概述

① 数据集。从MoocTest众包测试平台上选择4组真实的且包含测试工作量数据信息的缺陷数据集DS1～DS4。这4组众包测试数据集覆盖了不同数量的缺陷与测试人员，并且参与测试人员的数量都大于200，报告数量都大于1000，其成本数据远远超过传统测试。这些项目经过众包测试后，根据其互补性特点进行了测试报告、测试人力以及缺陷信息的统计与融合，形成了缺陷数据集，具体内容如表1所示。

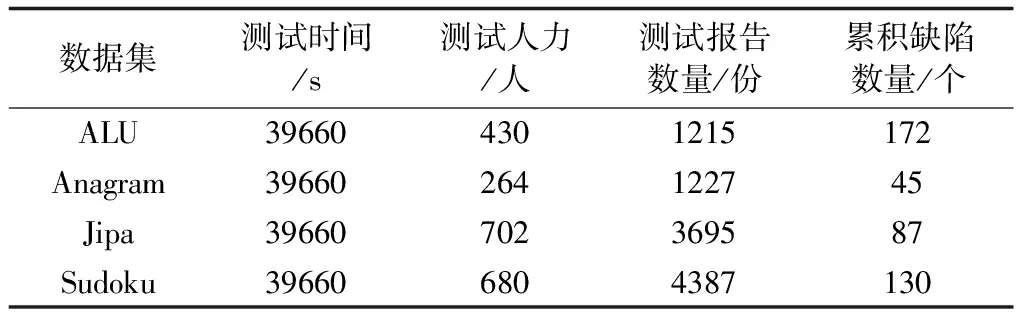
表1 众包测试缺陷数据集统计信息

② 对照组。选取现有的TE-SRGM作为基线方法，基线方法中测试成本工作量使用的TEF根据实验比较后选取最优分布函数。

③ 实验组。应用本文提出的CTDNEM分别建立适于真实数据集的缺陷数量估计模型，并与基线方法进行实例对比研究，其中测试成本工作量使用的TEF选择方法与对照组相同。

④ 参数估计方法。方法包括最大似然估计(Maximum Likelihood Estimation,MLE)和最小二乘估计(Least Squares Estimation,LSE)，其中TEF的参数估计仅使用LSE，累积检测缺陷数量函数表达式m(t)的参数估计使用MLE和LSE。

⑤ 任务结束判定规则。累积缺陷检测数量函数m(t)收敛，或者实际检测数量与软件潜在缺陷数量估计值a达到一定比例(如90%)，即可判定任务完成。

4.2 评价指标

为了检查TEF与CTDNEM的性能，更好地评估和比较模型拟合缺陷的力，实验使用以下3个评价指标。

(1)估算精度(Accuracy of Estimation,AE)。

AE通过软件中存在的初始估计的缺陷数和最终实际检测到的缺陷累积数进行计算，通过估计的软件潜在缺陷数量与检测结果的误差反映软件缺陷数量估计值的准确度。

(11)

式中，Ma为测试后实际检测到的缺陷累积数;a为估计的软件中的缺陷总数。估计值a最终可以用来与缺陷检测数量比较，衡量测试任务进度。

在党中央迁往当时北平的路上，毛泽东意味深长地说：这是“进京赶考”。“我们决不当李自成，我们都希望考个好成绩！”这考官自然是以工农为主体的人民大众。

(2)平方误差的均值(Mean Square Error,MSE)。

(12)

式中，mi为ti时刻的实际检测缺陷数；m(ti)为ti时刻模型估计的期望缺陷数。MSE越小，拟合误差越小，性能越好。

(3)预测效度(Predictive Validity,PV)。

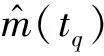
(13)

取不同的预计点te(te≤tq)，并重复上述过程，即可获得不同的RE(Relative Error)值。通常情况下，可以将不同的RE值制成RE图，以直观地检验模型的预计能力。RE图中接近于横轴(即RE值接近于0)的点越多，表明模型预计能力越好。

(4)缺陷覆盖率(Defect Coverage,DC)。

DC通过实时计算检测到的缺陷累积数和初始估计的软件缺陷数的比例，可以反映出缺陷被检测的覆盖程度。

(14)

式中，Ma为测试后实际检测到的缺陷累积数；a为估计的软件中的缺陷总数。理想状态下，当DC=100%时，缺陷全部被检测到。但是在实际测试中，DC总是小于理想值的，因此可以设定当DC达到某比例时，即可判定任务完成。

4.3 结果分析

为了验证所提出的模型CTDNEM，并与基线方法TE-SRGM进行性能比较，本文对4个实际的众包测试软件缺陷数据进行了实验，各个数据集的实验结果如下。

(1)DS1。

为了估计工作量，实验利用LSE方法对3种工作量函数进行参数估计。图3显示了通过使用上述3种TEFs来拟合估计的人力和测试报告的测试工作量，拟合曲线和实际软件数据分别用实线和虚线表示。

在图3(a)中，Logistic TE函数曲线与实际数据最为接近，其参数为W=391.70，A=7.870，α=0.107，k=3.5×10-3；在图3(b)中，Weibull-Type TE函数曲线与实际数据最为接近，其参数为W=1221.31，β=9.48×10-12，δ=2.564，θ=1.915。

通过相关系数计算公式得到测试人力和测试报告的相关性系数ρ=0.65，依据相关性系数实验选取可靠性模型框架中第2个微分方程求解。对已知的W(t)拟合曲线求导并代入方程，求解出m(t)公式。式中的其他参数可以通过MLE和LSE方法进行数值求解。然后将模型CTDNEM与基线方法进行对比，其参数估计和比较结果如表2所示。

表2 DS1的缺陷数量估计和性能比较结果

表2中，CTDNEM在MLE方法上估计结果的AE值为4.30%，MSE值为22.73，使用LSE方法估计结果的AE值为8.56%，MSE值为49.62。与基线方法相比，CTDNEM估计性能提升很大。根据上述结果，估计的累积缺陷数量如图4所示，最终预测缺陷数值开始收敛，且表2中的DC值已经超过了100%，说明该测试已经完成，符合实际情况。

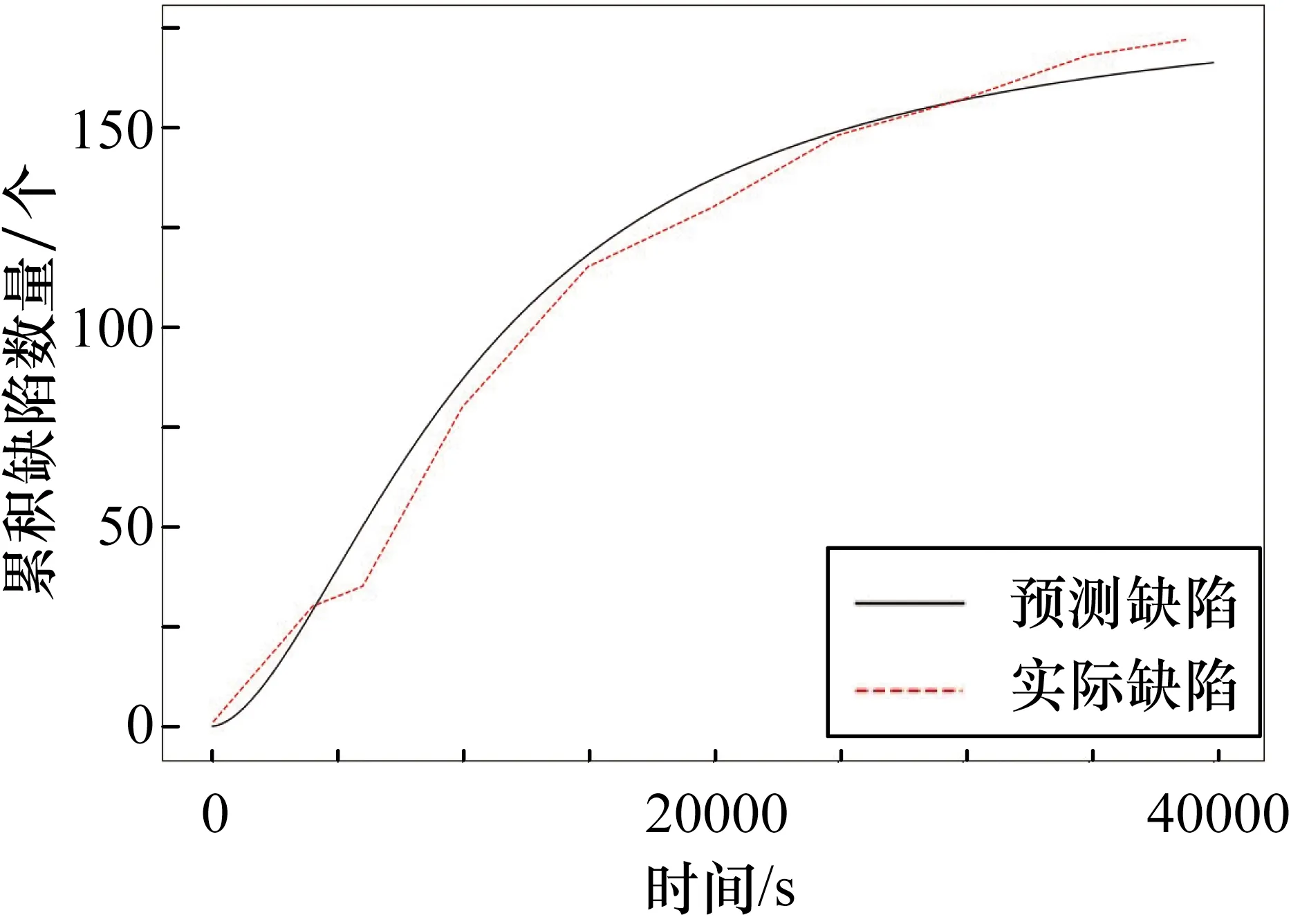
图4 DS1累积检测缺陷估计与实际数量

最后，计算该数据集预测效度，结果如图5所示。从结果观察到，相对误差随着时间增加逐渐接近于0，即最终预测值越来越准确。te/tq为50%时，准确性就已经在10%以内，te接近tq时，误差曲线通常也集中于10%以内，可以看出CTDNEM可以利用较少的实际数据预测出未来的缺陷检测数量，具有很高的估计准确性。

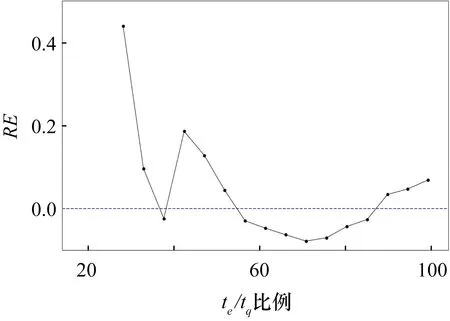
图5 DS1的RE曲线

(2)DS2。

DS2通过使用LSE来拟合估计的测试人力和测试报告的测试工作量如图6所示。

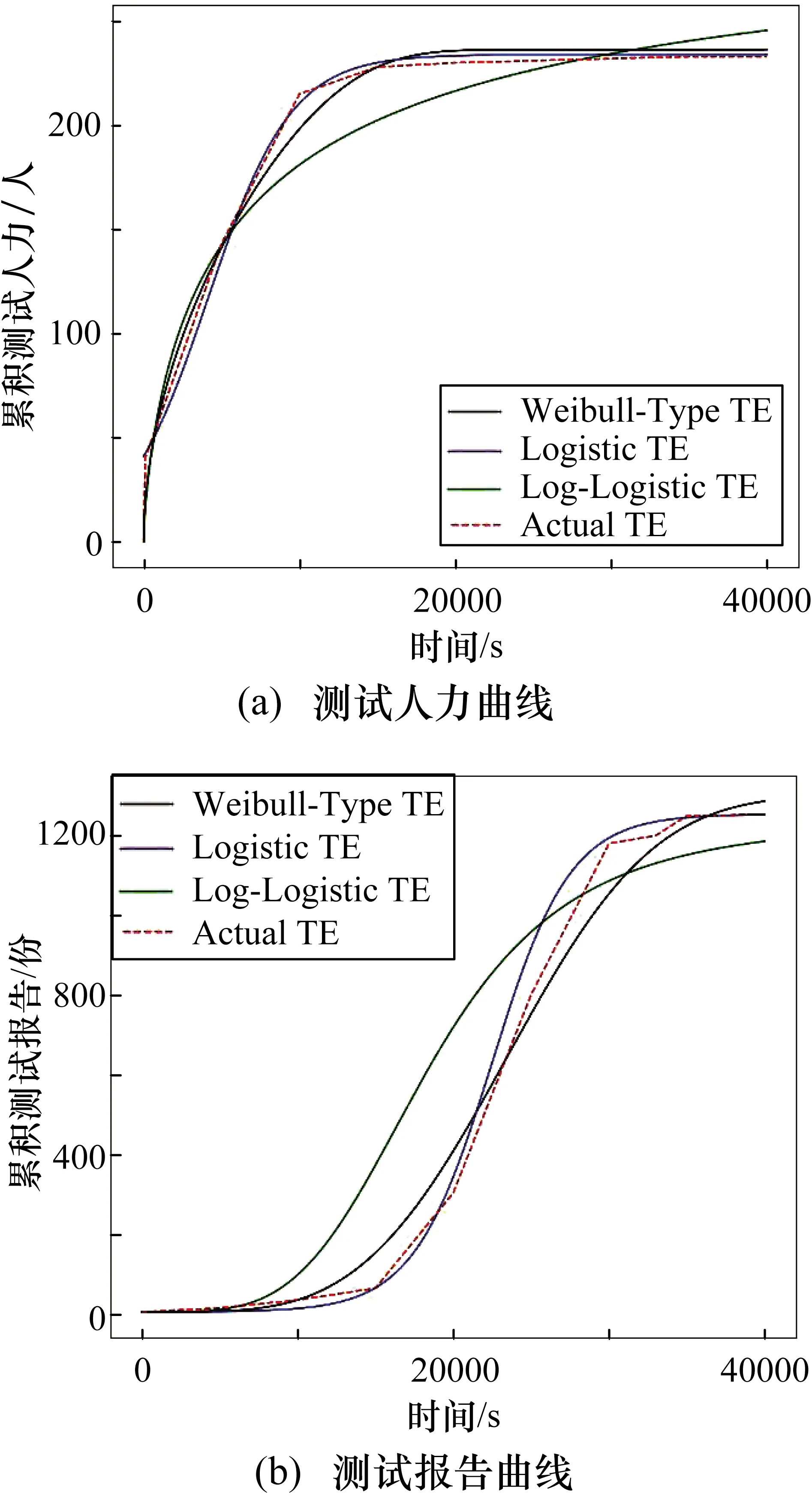
图6 DS2测试人力与测试报告的测试成本估计和实际数据

在图6(a)中，Logistic TE函数曲线与实际数据最为接近，其参数为W=233.99，A=4.719，α=1.38×10-2，k=2.72×10-2；在图6(b)中，Logistic TE函数曲线与实际数据最为接近，其参数为W=1253.88，A=7673.40，α=6.27×10-2，k=6.34×10-3。

依据计算得到测试人力和测试报告的相关性系数ρ=0.59，选取模型框架中第2个微分方程求解。模型CTDNEM与基线方法进行对比结果如表3所示。

表3 DS2的缺陷数量估计和性能比较结果

表3中，CTDNEM在MLE方法上估计结果的AE值为3.16%，MSE值为28.58，在相同方法下，基线方法估计结果的AE值仅为3.02%，MSE值为22.10。由此可见CTDNEM在该数据集中，没有很好地发挥出优势。根据参数结果，估计的累积缺陷数量如图7所示，与实际提交数据相符合。此时检测缺陷数量基本收敛，基线方法中DC值超过了90%，也可以判定测试任务完成，与实际情况相符。

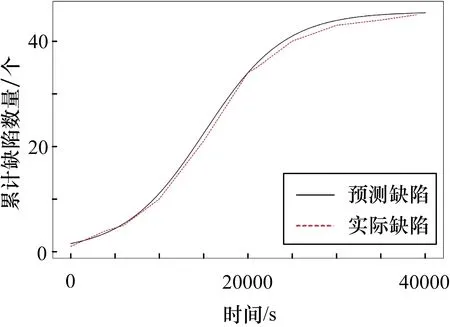
图7 DS2累积检测缺陷估计/实际数量

最后，预测效度的结果如图8所示，相对误差随着时间增加逐渐接近于0，在te/tq为60%时误差就已经在10%以内，可以看出CTDNEM具有很好的预测性，但是略逊于基线方法。

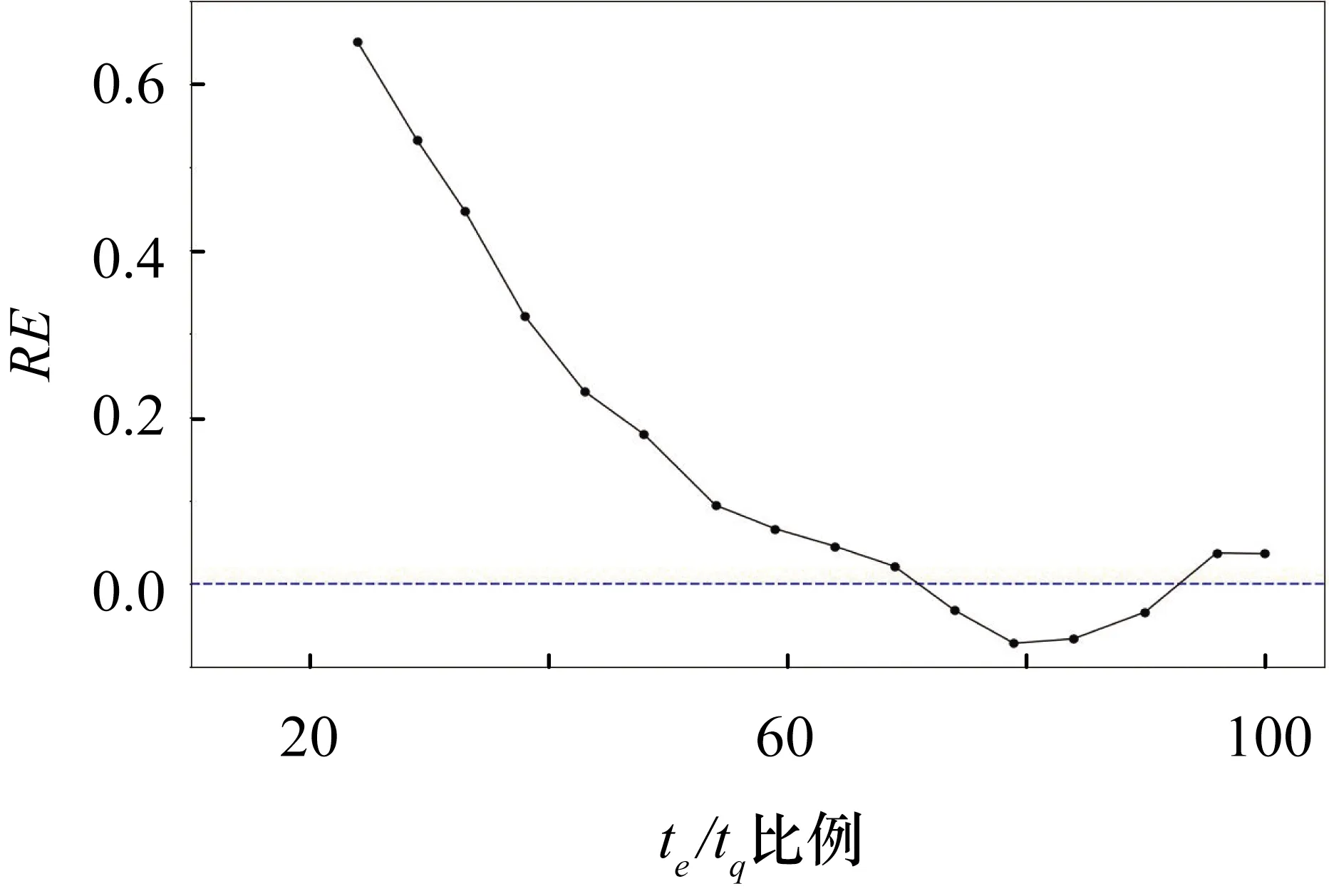
图8 DS2的RE曲线

(3)DS3。

DS3通过使用LSE来拟合估计的测试人力和测试报告的测试工作量如图9所示。

在图9(a)中，Logistic TE函数曲线与实际数据最为接近，其参数为W=636.74，A=2.060，α=3.05×10-2，k=1.05×10-3；在图9(b)中，Weibull-Type TE函数曲线与实际数据最为接近，其参数为W=4001.44，β=9.73×10-7，δ=1.397，θ=0.276。

图9 DS3测试人力与测试报告的测试成本估计和实际数据

依据计算得到测试人力和测试报告的相关性系数ρ=0.72，选取模型框架中第1个微分方程求解。CTDNEM得到的微分方程与基线方法一致，其结果如表4所示。

表4 DS3的缺陷数量估计和性能比较结果

表4中，CTDNEM使用MLE方法效果较好，估计结果的AE值为8.31%，MSE值为37.62，使用LSE方法的AE值为12.24%，MSE值为87.61。根据参数，估计的累积缺陷数量如图10所示，此时检测数量刚刚开始趋于平稳，而DC值在90%左右，由此判定测试关闭过早。

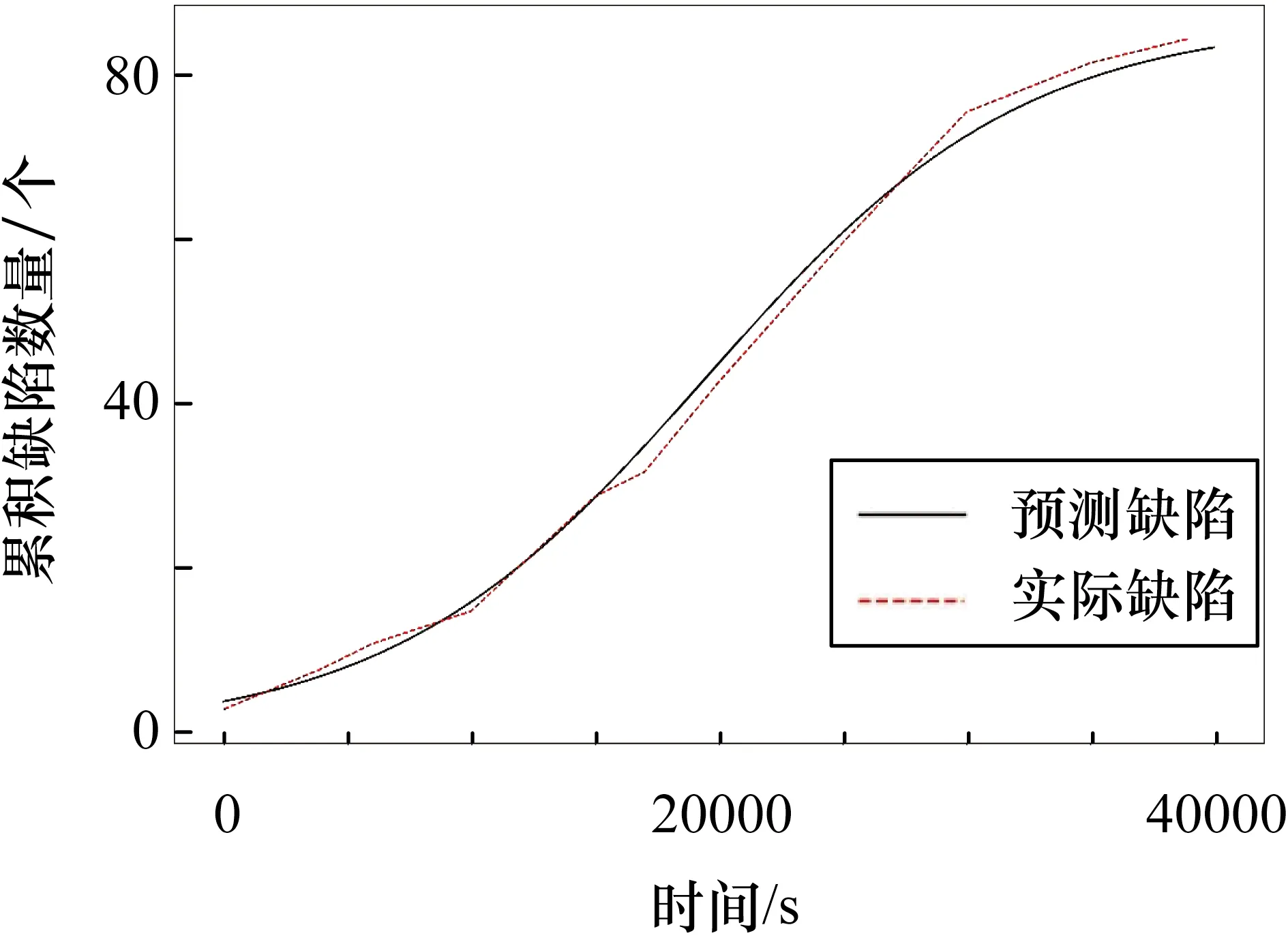
图10 DS3累积检测缺陷估计和实际数据

最后，预测效度的结果如图11所示，te/tq为50%时，准确性就已经在10%以内，可以看出CTDNEM能较好地对DS3缺陷数量进行估计。

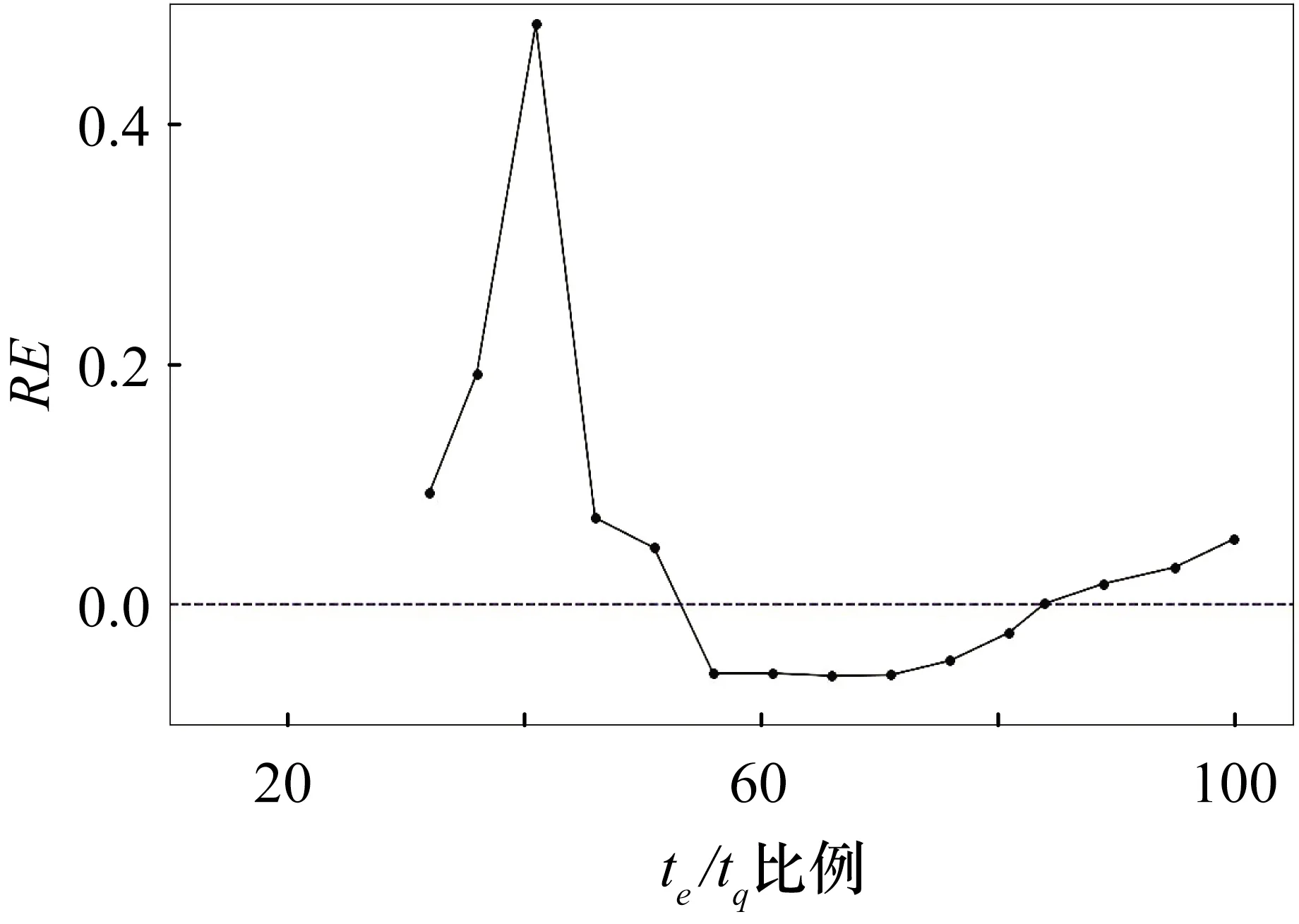
图11 DS3的RE曲线

(4)DS4。

DS4通过使用LSE来拟合估计的测试人力和测试报告的测试工作量，如图12所示。

在图12(a)中，Logistic TE函数曲线与实际数据最为接近，其参数为W=616.41，A=6.810，α=7.28×10-3，k=5.16×10-2；在图12(b)中，Weibull-Type TE函数曲线与实际数据最为接近，其参数为W=4395.53，β=2.815，δ=1.990，θ=0.357。

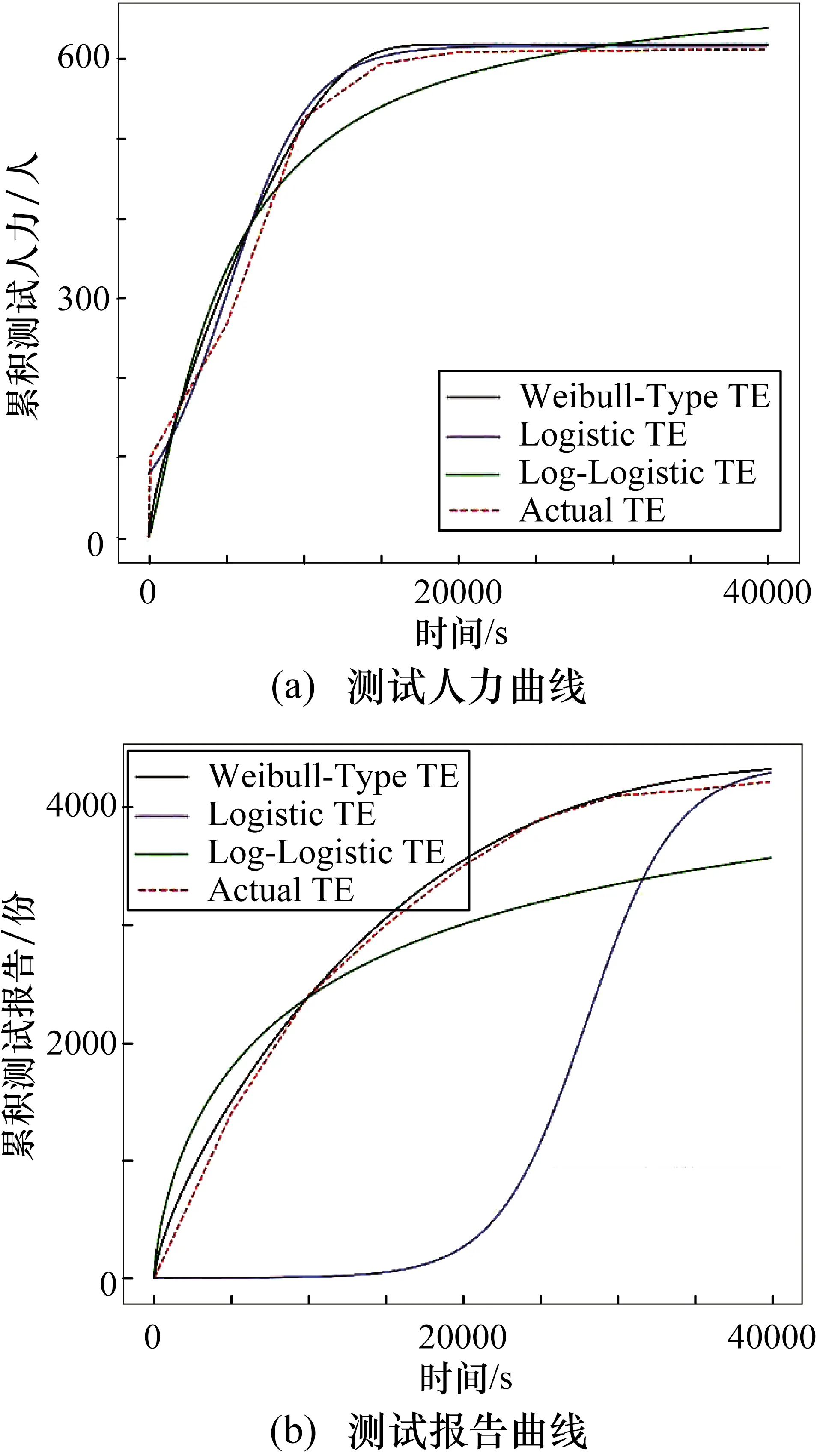
图12 DS4测试人力与测试报告的测试成本估计和实际数据

依据计算得到测试人力和测试报告的相关性系数ρ=0.66，选取模型框架中第2个微分方程求解。模型CTDNEM与基线方法进行对比结果如表5所示。

表5 DS4的缺陷数量估计和性能比较结果

表5中，CTDNEM使用MLE方法效果较好，估计结果的AE值为3.61%，MSE值为29.72;使用LSE方法的AE值为8.56%，MSE值为51.55。两种方法的结果皆优于基线方法性能。根据参数，估计的累积缺陷数量如图13所示，累积检测缺陷数量已经开始收敛，且DC值皆高于90%，测试完成程度较高。

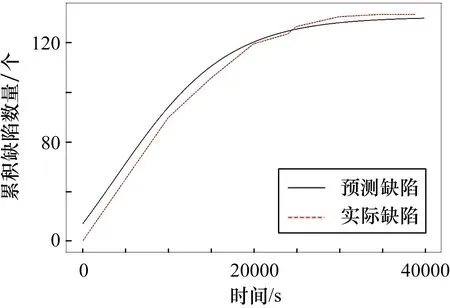
图13 DS4累积检测缺陷估计和实际数据

最后，预测效度的结果如图14所示，te/tq为50%时，准确性就已经在10%以内，当te接近tq时，误差曲线主要集中于5%以内，可以看出CTDNEM估计结果的准确性高。

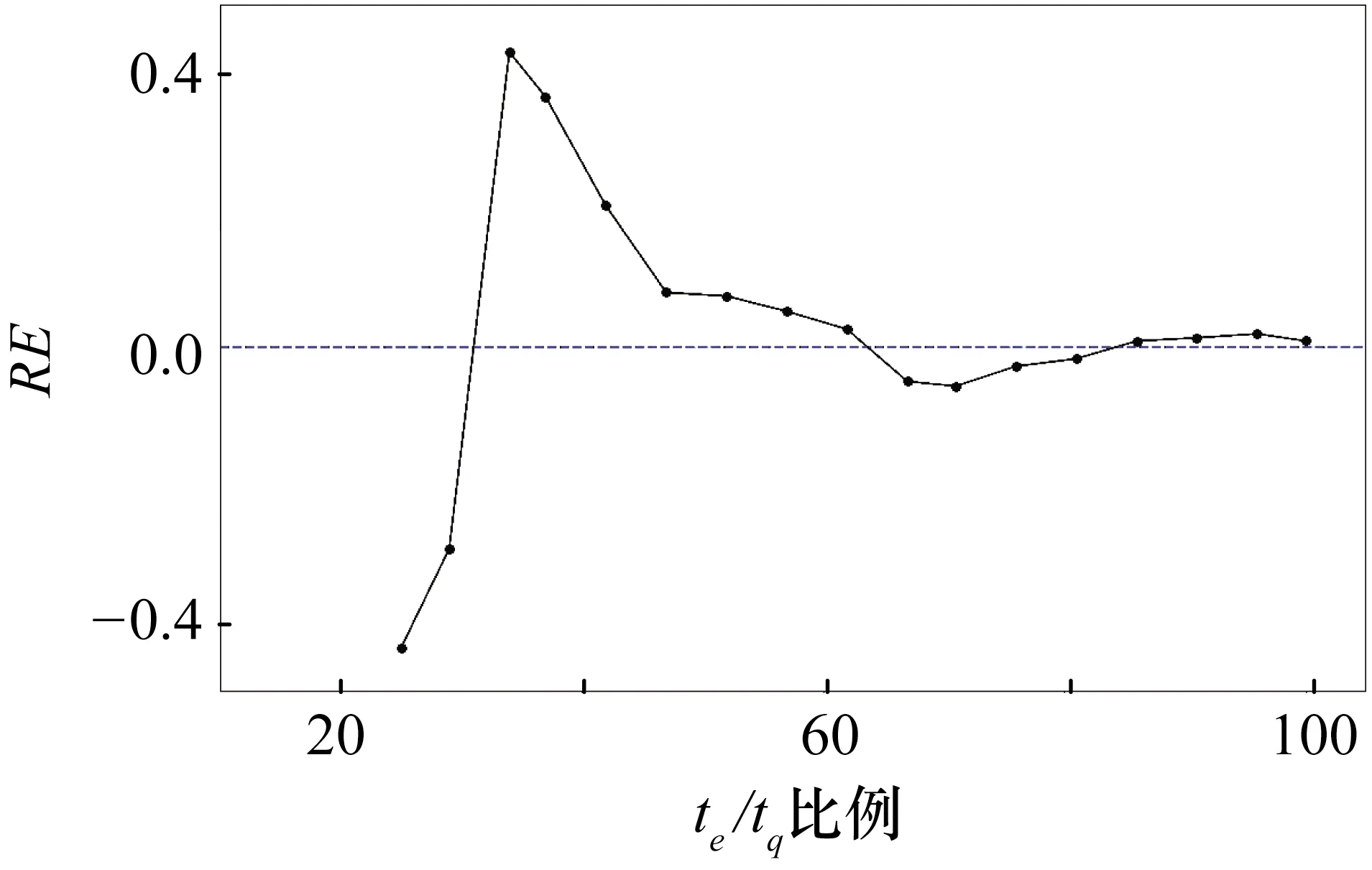
图14 DS4的RE曲线

综上所述，CTDNEM在4个众包测试数据集上进行了实验，所有测试人力数量满足Logistic TE函数曲线，大部分测试报告数量满足Weibull-Type TE函数曲线。累积检测缺陷数量在3个数据集上的估计效果皆表现出良好的性能，在DS2数据集上逊色于基线方法。4个实验的误差曲线在te/tq为50%时，误差都小于10%，表明模型能用较少的数据准确评估任务完成度，由此可见CTDNEM能够很好地对众包测试数据集的缺陷进行预估。

5 结束语

众包测试中，测试人力和测试报告提交数量是衡量测试成本的两个重要元素。为了能够通过完成缺陷数量的实时预估以监控众包测试任务的过程，本文提出了一个同时考虑两个测试成本元素的众包测试缺陷数量估计模型。在此基础上，结合已有的3种测试工作函数，对如何利用新的可靠性建模框架在众包测试数据集建模的过程进行了分析。在4组真实的众包测试数据集上，利用CTDNEM进行了缺陷数量估计实验，并将典型的TE-SRGM模型作为基线方法对估计性能进行了对比。由对比结果可知，CTDNEM的拟合与估计结果在3组数据集上均表现良好，对4组测试任务关闭时间评估符合实际情况。由此可知，CTDNEM有更好的缺陷预估能力，在实际的众包测试中对监控测试任务过程、决策任务结束时间具有重要的指导意义。