基于有限元的膨胀管膨胀过程力学分析
2021-09-28罗建伟邢洪宪李瑞丰王新涛鞠少栋刘传刚
刘 鹏,罗建伟,邢洪宪,李瑞丰,王新涛,鞠少栋,刘传刚
(中海油能源发展股份有限公司 工程技术分公司,天津 300452)
在进行膨胀管大通径注水工艺中,利用膨胀管的悬挂和密封原理设计了膨胀悬挂封隔装置,该装置的核心部件是膨胀管。通过膨胀锥对膨胀管的膨胀,实现完井管柱的悬挂和密封[1-2]。在膨胀过程中,膨胀管自身应力发生变化,膨胀后膨胀管内径和外径被膨胀锥膨胀,使膨胀管的厚度和长度在数值上发生变化。由于膨胀管膨胀后内部存在残余应力,会导致膨胀后的膨胀管出现变形和开裂等问题[5-7]。为研究膨胀过程的力值变化、膨胀管外形尺寸的变化,以及管内的残余应力,本文对膨胀管和膨胀锥进行三维建模,通过ANSYS软件对膨胀过程进行有限元分析,得到膨胀过程相关参数的变化,为现场施工提供理论基础[8-10]。
1 膨胀过程三维建模
1.1 几何模型建立
膨胀锥结构如图1所示。膨胀锥大径ø139.2 mm,膨胀率12.3%。膨胀管尺寸为140 mm×8 mm。图2是ANSYS中采用的2D轴对称模型。表1是模型尺寸主要参数。
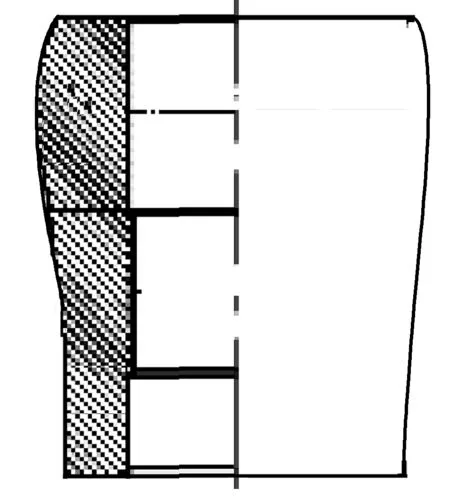
图1 膨胀锥结构
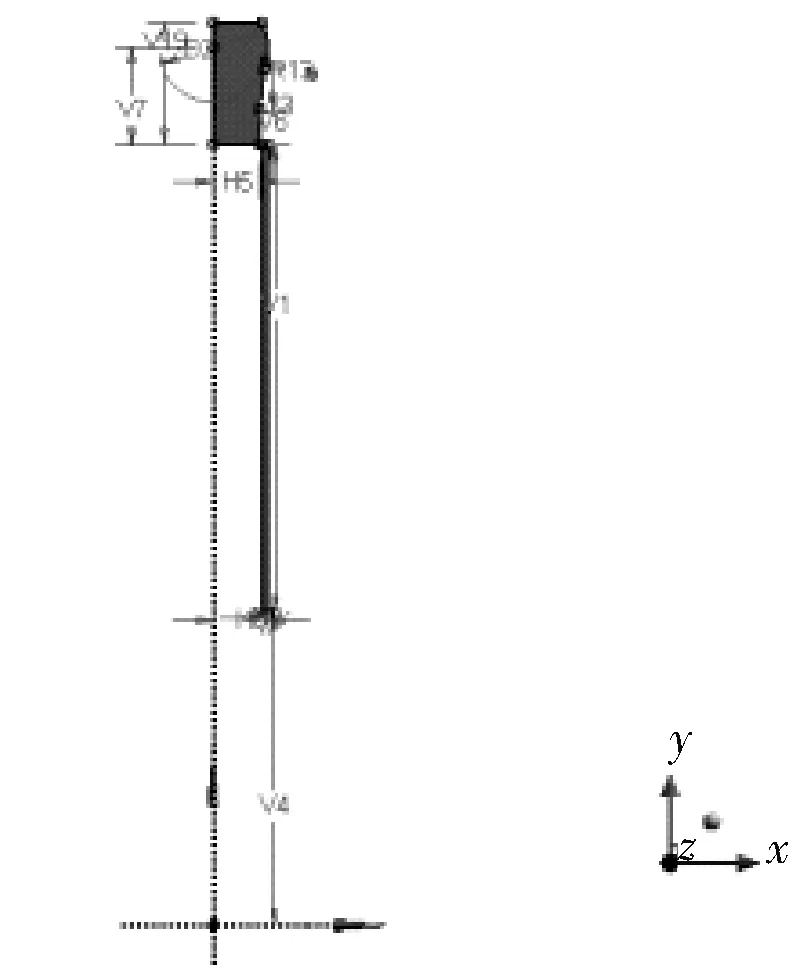
图2 ANSYS中采用的2D轴对称模型

表1 模型尺寸参数
1.2 材料属性输入
设定膨胀管材料弹性模量E=210 Gpa,泊松比0.3。对膨胀管样件进行单向拉伸试验,数据如表2。材料屈服强度为217 MPa,抗拉强度445 MPa。由于套管在膨胀过程中发生大的塑性变形,涉及材料非线性问题,为了真实反映膨胀管材料性能,采用膨胀管样件拉伸试验数据,以名义应变εnom和名义应力σnom表示。为了准确地描述膨胀套管大变形过程中截面面积的改变,需要使用真实应变εtrue和真实应力σtrue,及塑性应变εpl,相互之间的换算如式(1)~(3),延伸率相当于材料的名义应变值。

表2 试样拉伸性能试验结果
εtrue=ln(1+εnom)
(1)
σtrue=σnom(1+εnom)
(2)
(3)
转换后膨胀套管材料真应力-应变曲线如图3所示,并在真实应力-应变曲线中提取真实应力、应变点,建立有限元分析用膨胀管材料性能参数。膨胀锥材料按照刚性体进行计算。
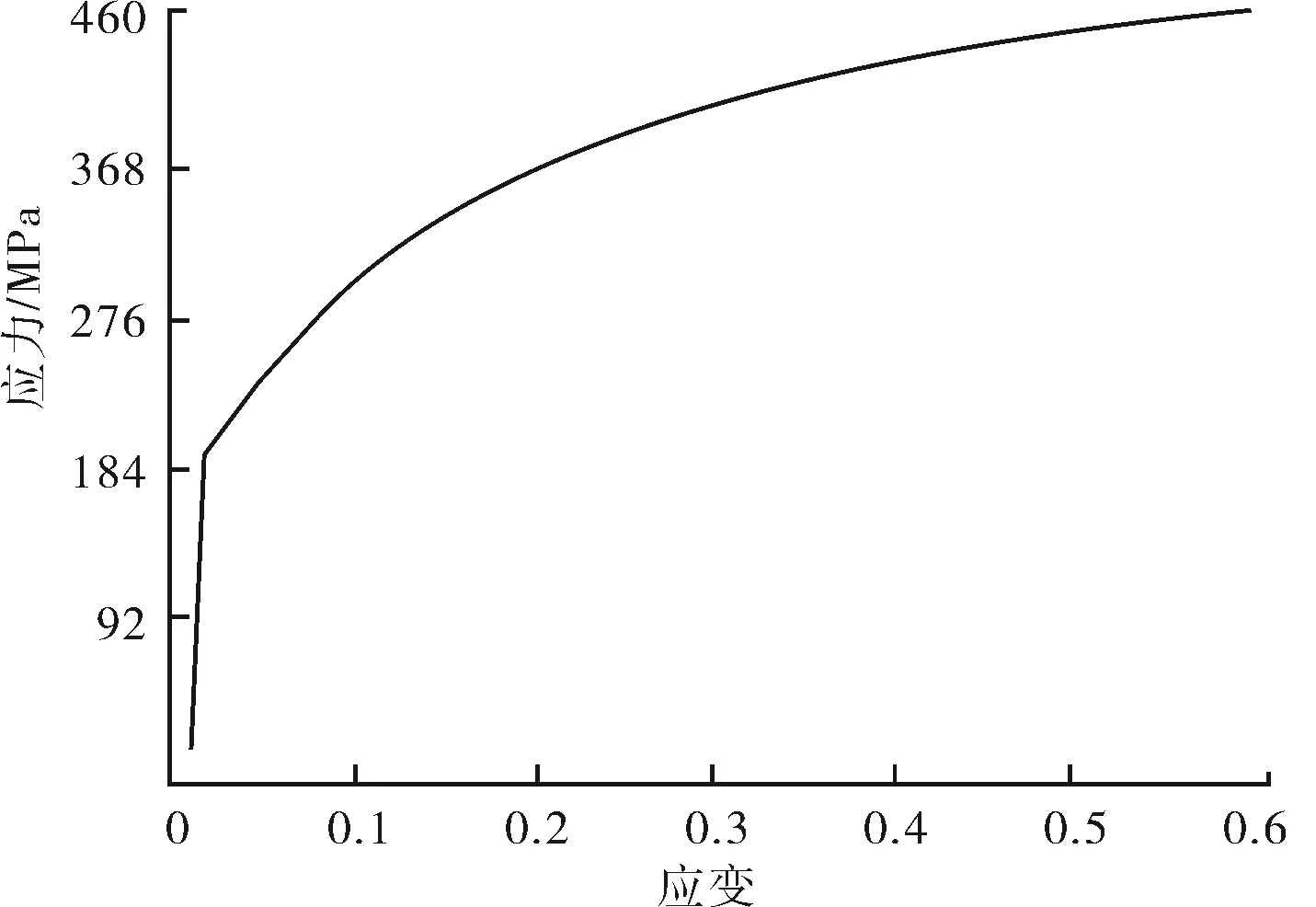
图3 计算用膨胀管材料拉伸性能曲线
1.3 网格划分和约束加载
分析过程中,主要关注膨胀管的受力和变形情况,特别是膨胀管在径向的变形情况,因此膨胀管在厚度方向网格加密。为了提高计算效率,在长度方向可适当增大网格密度。
图4是模型约束加载设置,对膨胀管顶端(C端面)和膨胀锥中心轴(B端面)设置无摩擦约束,膨胀锥端面(A端面)设置向下位移,开启大变形设置,设置载荷步。膨胀管和膨胀锥之间采用frictionnal接触设置,摩擦因数0.1,采用Augmented Lagranges算法。
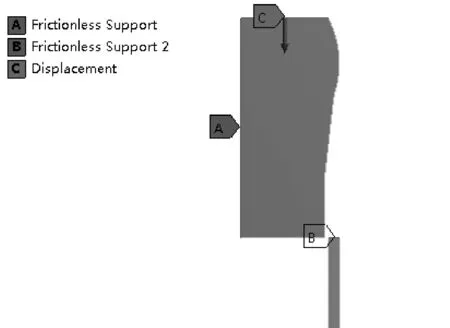
图4 施加约束
2 膨胀结果分析
2.1 膨胀管应力分布
图5是膨胀锥不同位置时膨胀管的应力分布情况,可以看出膨胀锥膨胀变形区域应力最大,当膨胀锥离开膨胀管后,膨胀管应力分布趋于均匀。

图5 膨胀管过程中膨胀管应力分布
图6是不同时刻膨胀管内表面各位置应力曲线,可以看出,在膨胀锥不同位移时刻,膨胀阶段与膨胀区接触区域的内表面应力值最大,当膨胀锥离开膨胀管后,膨胀管内表面应力值迅速下降。
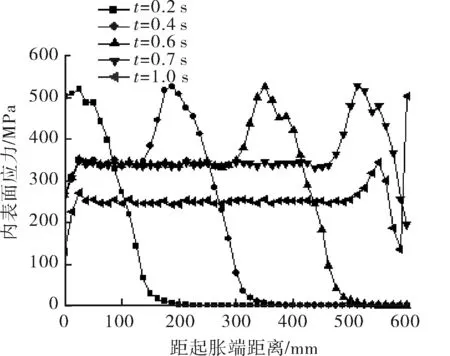
图6 不同时刻膨胀管内表面各位置应力分布
2.2 膨胀力求解
图7是利用膨胀管端面的约束反力等效求解膨胀锥所需驱动力,即膨胀力;图8是提取有限元计算结果中膨胀力与膨胀锥位移的变化曲线,起胀阶段,随着膨胀锥与膨胀管接触,膨胀力线性增大。膨胀锥完全进入后,膨胀力趋于稳定,膨胀力为340 kN。当膨胀锥完成膨胀过程,离开膨胀管,膨胀力下降为0,稳定阶段所需膨胀力数值为研究所需膨胀力。

图7 膨胀力求解
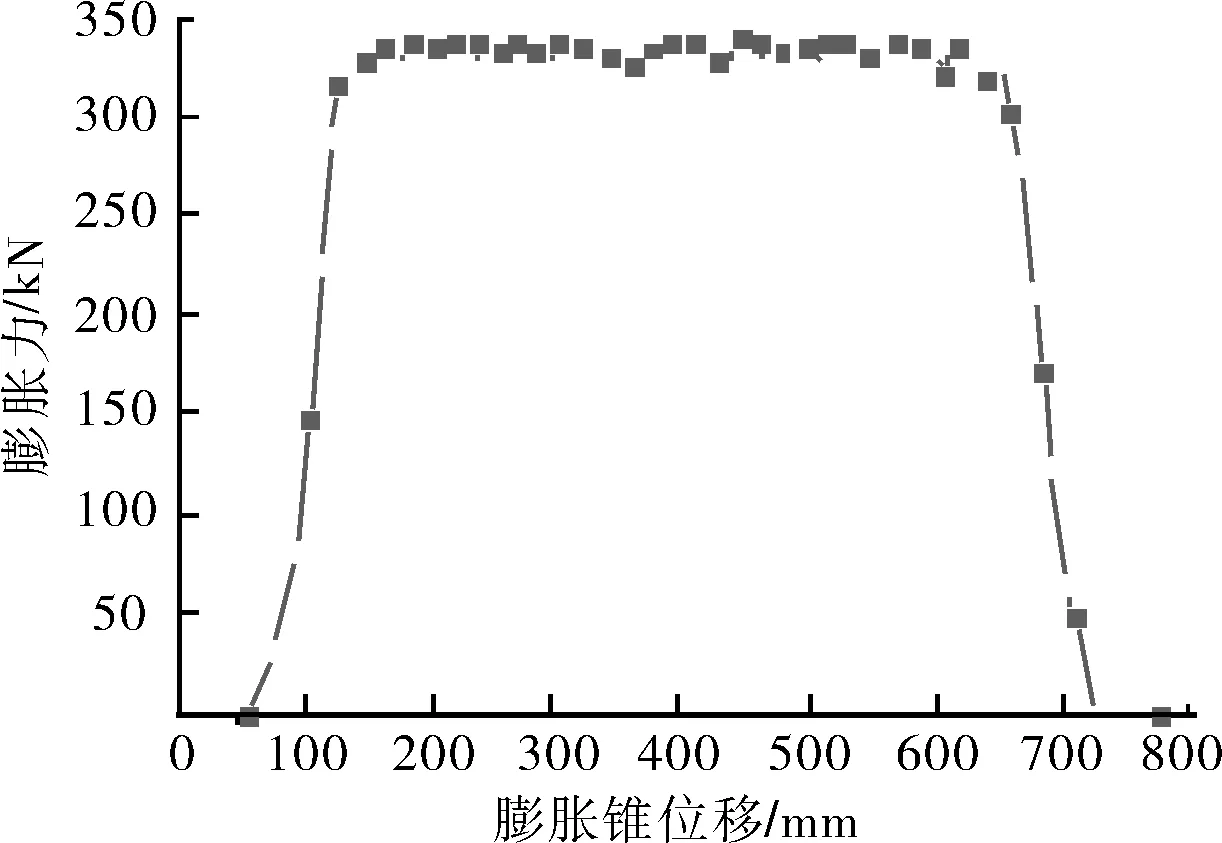
图8 膨胀力与膨胀锥位移曲线
2.3 轴向收缩量
膨胀管在膨胀过程中随着内外径增大,轴向会发生收缩。图9是利用膨胀管下端面的轴向变形计算轴向收缩量;图10是轴向收缩量随膨胀锥位移的变化曲线,膨胀过程中轴向收缩量随膨胀锥位移呈线性增长,在膨胀锥离开膨胀管时刻轴向收缩量最大,为20.62 mm。当完全离开膨胀管后,收缩量略有下降并稳定,最终的轴向收缩量为20.15 mm。

图9 轴向收缩量求解图
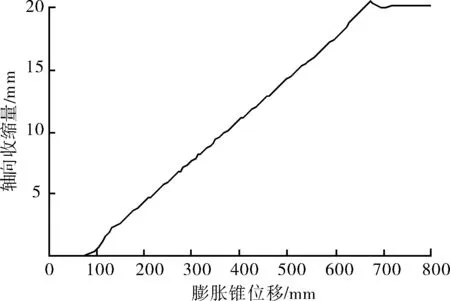
图10 轴向收缩量-膨胀锥位移曲线
2.4 壁厚变化
膨胀管在膨胀过程中随着内外径增大,壁厚会发生减薄。图11是膨胀后膨胀管内外壁位移随膨胀管位置的变化曲线,可以看出内壁的位移要大于外壁位移,所以发生壁厚减薄,二者的差值及壁厚减薄量,平均减薄量为0.59 mm;图12是膨胀后膨胀管壁厚随膨胀管位置的变化曲线,膨胀管端部壁厚出现极值,这是由于膨胀锥离开的端部发生了缩口导致的结果,计算得出膨胀后壁厚平均值为7.41 mm。
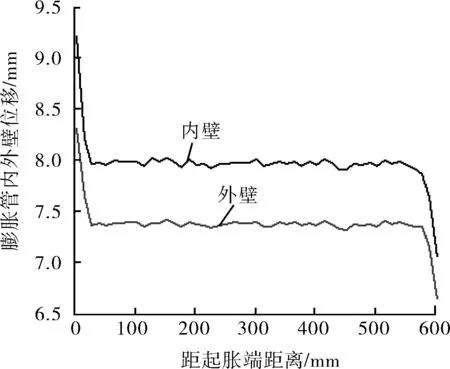
图11 膨胀后膨胀管不同位置内外壁位移量
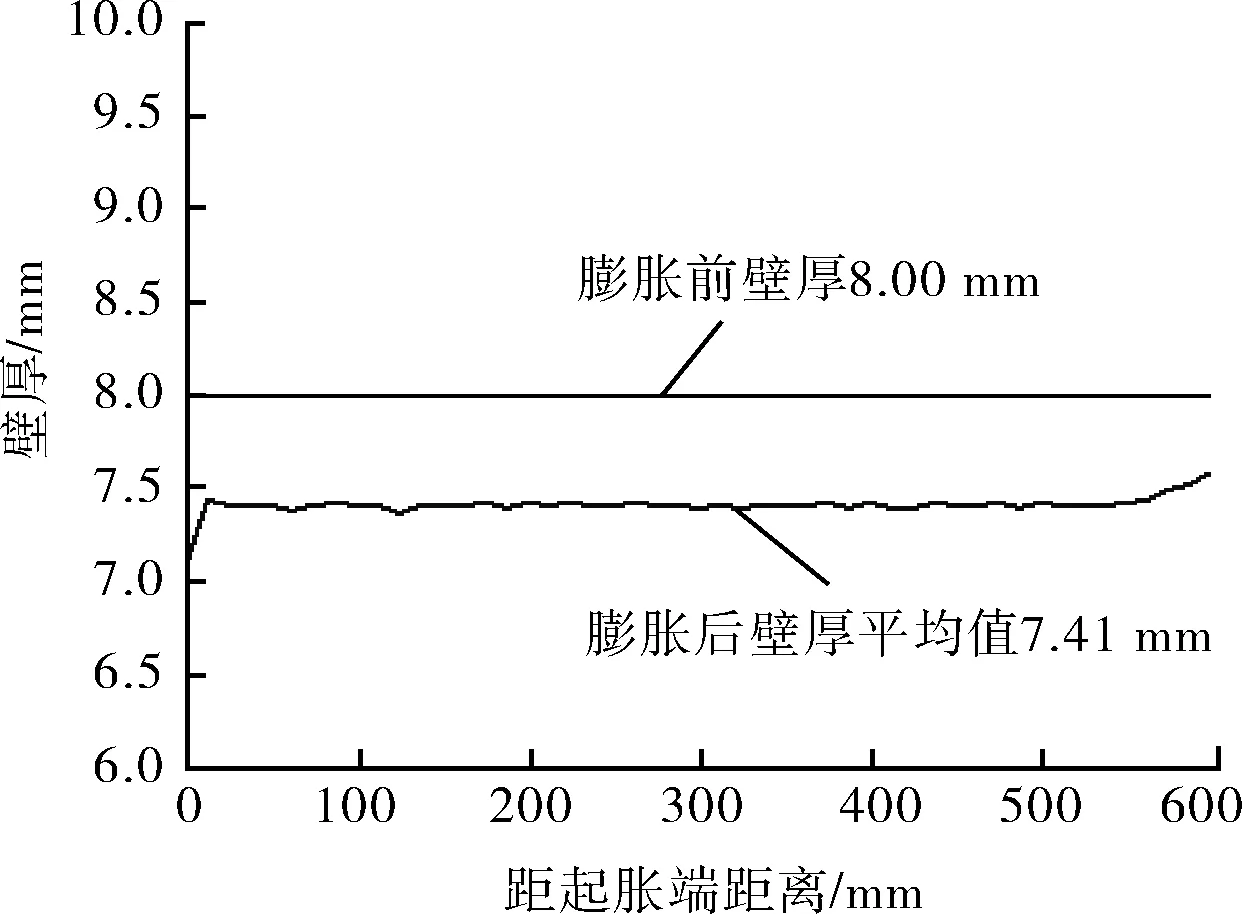
图12 膨胀后膨胀管壁厚-位置曲线
2.5 残余应力分析
残余应力是消除外力或不均匀的温度场等作用后仍留在物体内的自相平衡的内应力。机械加工和强化工艺都能引起残余应力。例如冷拉、弯曲、切削加工、滚压、喷丸、铸造、锻压、焊接和金属热处理等,因不均匀塑性变形或相变都可能引起残余应力。
对于膨胀管而言,膨胀管在膨胀过程中发生冷扩径塑性变形之后,D/t值将增加,由于金属Bauschinger效应,应力-应变曲线形状也会由于塑性变形的影响发生变化,同时由于塑性变形附加的残余应力不均匀地分布在套管的整个横截面上,而残余应力也是影响膨胀套管的抗外挤强度的主要因素。
图13~14是膨胀后膨胀管内外表面残余应力的分布情况。图15是膨胀后膨胀管内外壁残余应力随膨胀管位置的变化曲线,可以看出内外表面残余应力随膨胀管位置的变化趋势是一致的,外表面残余应力大于内表面,但在膨胀锥离开膨胀管的端部(缩口位置)时内表面的残余应力大于外表面,外表面残余应力极值都出现在膨胀锥离开膨胀管的位置,内表面残余应力极小值出现在起胀端,极大值位于膨胀锥离开膨胀管的位置,具体数值如表3。

图13 膨胀后内表面残余应力分布

图14 膨胀后外表面残余应力分布
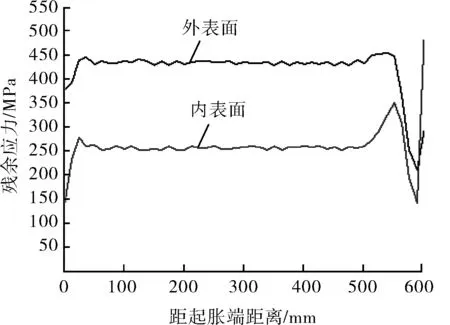
图15 膨胀后不同位置内外表面残余应力分布曲线
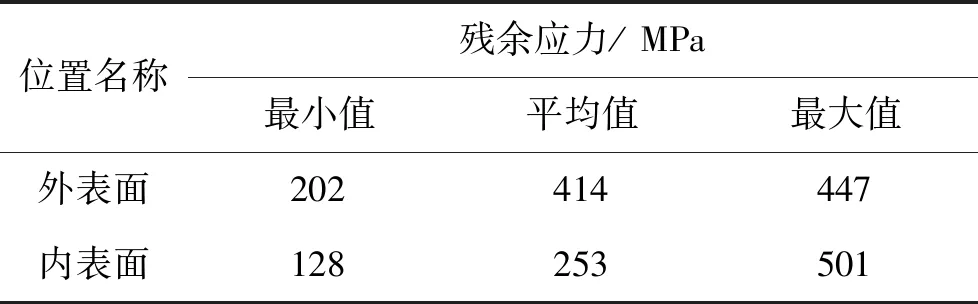
表3 膨胀后内外表面残余应力值
图16是残余应力与壁厚方向位置的变化曲线,可以看出在厚度方向残余应力的变化趋势,最小值出现在1/2壁厚附近,沿壁厚方向呈上升—下降—上升过程。
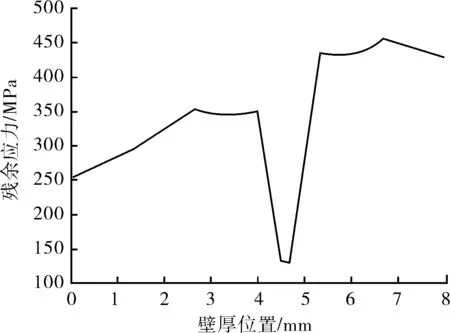
图16 膨胀后壁厚方向不同位置残余应力变化曲线
3 结论
1) 本文对膨胀管和膨胀锥进行三维建模,采用ANSYS软件模拟了膨胀过程,并得到膨胀管的应力分布、膨胀力值、残余应力、轴向收缩量以及壁厚变化。
2) 在胀过程中,膨胀管的轴向收缩量随膨胀锥位移呈线性增长。在膨胀锥离开膨胀管时刻,其轴向收缩量最大。当完全离开膨胀管后,该收缩量略有下降并稳定。
3) 膨胀管在膨胀过程中随着内外径增大,壁厚会减薄,内壁的增值大于外壁增值,膨胀管端部壁厚出现极值。
4) 内外表面残余应力变化趋势相同。在厚度方向,残余应力呈上升-下降-上升过程趋势,最小值出现在1/2壁厚附近。
