减小OVT片尺度的技术及应用

瞿长青,王东奎,王忠军,马建波,窦安迪

(中国石油化工股份有限公司中原油田分公司物探研究院,河南濮阳457001)

近年来,随着地震勘探目标愈趋复杂、地质要求不断提高,宽方位高密度地震勘探逐渐成为地震勘探的发展方向,作为面向宽方位地震资料的处理方法之一,OVT域地震资料处理越来越受到关注。

OVT(offset vector tile)通常被翻译成炮检距向量片,又称为共偏移距向量(common offset vector,COV)。OVT概念最早由VERMEER[1]在研究十字排列最小数据集时提出,因为OVT道集具有相近的偏移距和方位角,所以OVT道集也称为共偏移距共方位角道集,OVT是十字排列道集内的一个数据子集。在每一个十字排列上按照炮线距和检波线距来划分OVT片,每个OVT片都是沿炮线有限范围内的炮点和沿检波线有限范围内的检波点构成,OVT具有限定范围的偏移距和方位角[2]。将具有相同编号的OVT片组成OVT道集,这个OVT道集是均匀的,是覆盖全工区的一次覆盖。OVT道集的个数与满覆盖次数相等。

因为OVT道集由具有大致相同的炮检距和方位角的地震道组成,而且延伸到整个工区,是覆盖整个工区的单次覆盖数据体,因而可以独立叠前偏移成像,偏移结果可以保存方位角和偏移距信息,适用于方位角分析,总的来说,OVT域处理具有如下优势:①OVT道集是目前唯一能延伸到整个工区的单次覆盖数据集;②OVT道集一致性较好,可真实保留原始数据采集特征;③OVT偏移后近、中、远道能量一致,振幅特征好,有利于反演;④OVT道集具有炮检互换性;⑤OVT域偏移后能保留方位角信息。

虽然OVT域处理具有诸多优势,但其对原始采集资料的要求较高,理论上讲,每一个OVT片都具有相近偏移距和方位角,不过这是基于野外采集资料时的炮线距和接收线距较小的情况,但当前地震资料处理所面对的地震资料,特别是老资料重处理,原始地震资料炮线距和接收线距较大,即OVT片尺度较大,造成一个OVT片内的偏移距和方位角范围也较大,由此势必影响一个OVT片内偏移距和方位角的一致性,从而影响最终OVT域处理效果,这极大地限制了OVT域处理技术的推广应用。针对如何进一步提高OVT域处理效果,邵文潮等[3]通过研究OVT域处理技术在塔河地区的应用,提出在采集炮线距和检波线距设计时充分考虑OVT域偏移后最小偏移距(最小入射角)的大小。田忠斌等[4]研究了OVT域处理技术在沁水盆地深部煤层气勘探中的应用,通过优化OVT道集分选、OVT域五维插值等技术手段,提高OVT域处理效果。印兴耀等[5]系统论述了OVT域地震资料五维解释的理论基础。段文胜等[6]采用匹配追踪傅里叶插值技术,在五维数据空间实现了基于原始观测系统的数据重构,解决了大范围数据的不规则采样问题。孙苗苗等[7]研究了基于曲波域稀疏约束的OVT域地震数据去噪方法,提高了OVT域处理剖面的信噪比。李博[8]通过分选OVT域数据的排列特征,提出了一种基于非规则傅里叶变换的最小平方反演数据重建技术及实施流程。王伟等[9]通过实际工区应用,研究了五维规则化技术及应用效果。夏亚良等[10]研究了OVT域方位各向异性技术在中非花岗岩裂缝预测中的应用,验证了方位各向异性井震联合花岗岩裂缝预测方法的可靠性。袁刚等[11]研究了OVT域偏移道集的校平方法。

本文在OVT域处理阶段,联合应用五维插值加密检波线技术和基于对折法的OVT片优化技术,使OVT片尺度减小一倍,减小OVT道集内偏移距和方位角范围,增强了OVT道集偏移距和方位角属性的一致性,提高OVT域处理效果。

1 方法技术

1.1 五维插值技术

常规三维数据插值主要在共中心点域进行重构,只能针对偏移距或者方位角中的一个维度进行处理,不能同时针对偏移距和方位角进行处理[12],而五维空间的数据插值同时考虑到时间、空间、偏移距和方位角变化等,确保了叠前数据随偏移距和方位角的相对保持振幅[13]。

五维插值基于空间真实坐标,充分利用数据的五个维度信息,在炮检域加密炮线、炮点、检波线和检波点,可在一定程度上弥补地震数据采集不足的问题。五维插值算法实际上是求解一个大型的反问题,正问题可以用下式表达:

d=Tx

(1)

式中:x是理想充分采样的五维数据体;d是实际地震记录的波场;T是采样算子。采样算子将理想充分采样的五维数据体映射到实际数据。实际求解时,它同时在五维空间执行正向不规则傅里叶变换,以建立频率域的数据。反变换是一个欠定方程,通过最小目标函数求解:

J=‖d-Tx‖2+λ‖x‖1

(2)

式中:‖x‖1为L1范式;λ为正则化系数(λ≥0)。

L1范式可以产生比较稀疏的解,具备一定的特征选择的能力,对高维特征空间进行求解时比较有用,五维插值的求解问题实际就是求解方程(2),使J最小,正则化系数λ的选择主要基于原始地震数据的噪声水平,在实际处理过程中需要对原始地震数据进行测试,一般选取5%～30%。

本次五维插值处理主要基于傅里叶重构技术,数据处理时充分利用数据的5个维度信息,在炮检域加密检波线。在实际应用过程中,对频率-空间域的数据进行操作,采用迭代算法,每一次迭代从冗余空间中选取一个傅里叶分量。首先利用内积运算寻找能量最大的频率成分,然后将该成分数据减掉得到更新后的数据,利用该数据再去求下一个最大能量的频率成分,如此反复,直至得到所有的频率成分为止,从而得到无频谱泄漏的所有频率成分,然后再进行反变换,得到规则化后的地震数据。

反变换可以将数据输出到一个规则的网格上,即所谓的全规则化,也可只沿需要填补的炮检线位置,生成新的数据,该方法需要保留原始数据,而不是完全被全规则化的数据所取代,在原始数据很稀疏或对数据规则化的保真性有更多关注时采用。因为插值毕竟是欠定问题,不确定性始终存在,它依赖于算法对波场描述的精度[13]。

1.2 基于互换原理的对折法OVT片优化技术

OVT道集具有良好的炮检互换性,所谓炮检互换性,是指在相似的大地耦合条件下,从位置A激发的炮点到位置B接收的检波点地震道与从位置B激发的炮点到位置A接收的地震道相同(图1,图中浅蓝色区域分别为两个十字排列的一次覆盖区域,黄色方块为两个十字排列重叠覆盖区),即在相同位置进行炮检点互换,由于炮检点旅行时的和相等,认为地震道可以互换,而且不改变偏移距及方位角信息[13]。对于观测系统满覆盖区的2次覆盖数据体,可以由坐标对称的OVT构成,从中也能观测到OVT的互补性,某个十字排列的炮点轴可以和另一个十字排列的检波点轴形成一个新的十字排列数据,反之亦然。

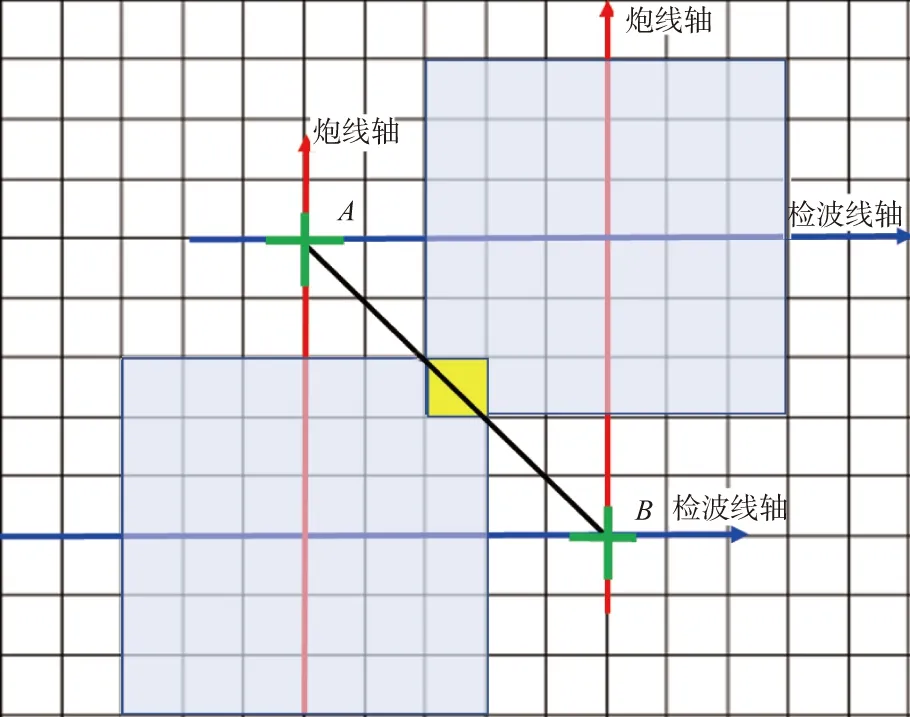
图1 炮检互换原理

基于互换原理的对折法OVT片优化技术是对两个十字排列重叠区域可以互换的两个OVT片,先将其中一个OVT片以十字排列中心点沿检波线方向旋转180°,然后重叠在一起,沿OVT片中心线顺着检波线(炮线)方向进行对折,以实现将检波线(炮线)方向OVT片尺度减小一半的目的(图2和图3)。

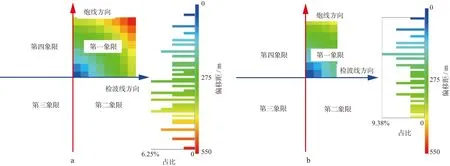
图2 两个可互换OVT片对折前(a)、后(b)(第一象限)

图3 两个可互换OVT片对折前(a)、后(b)(第三象限)

当然,此种方法也存在一定弊端,即当两个可互换的OVT片在平面上并不完全重合时,会带来空白面元的问题(图4和图5),虽然空白面元部分主要集中在不满次覆盖区,但空白面元的范围尺度能达到半个偏移距,在实际应用过程中应予以关注。

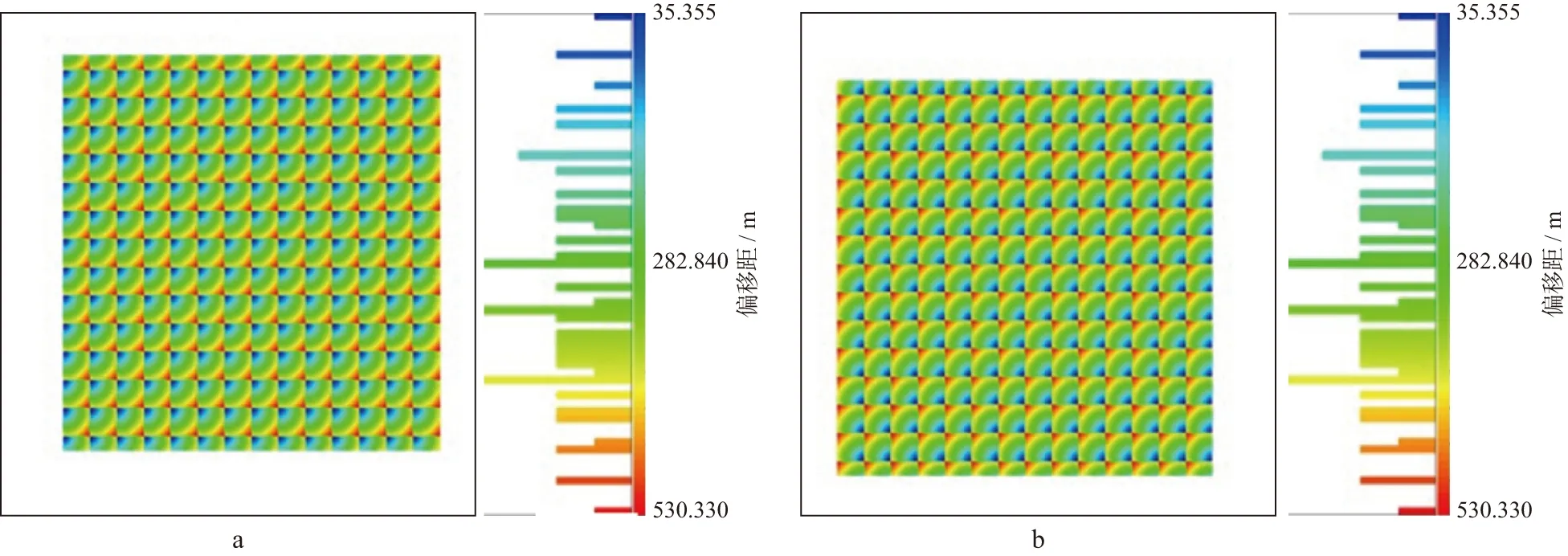
图4 两个可互换OVT片对折前分布a 第一象限; b 第三象限

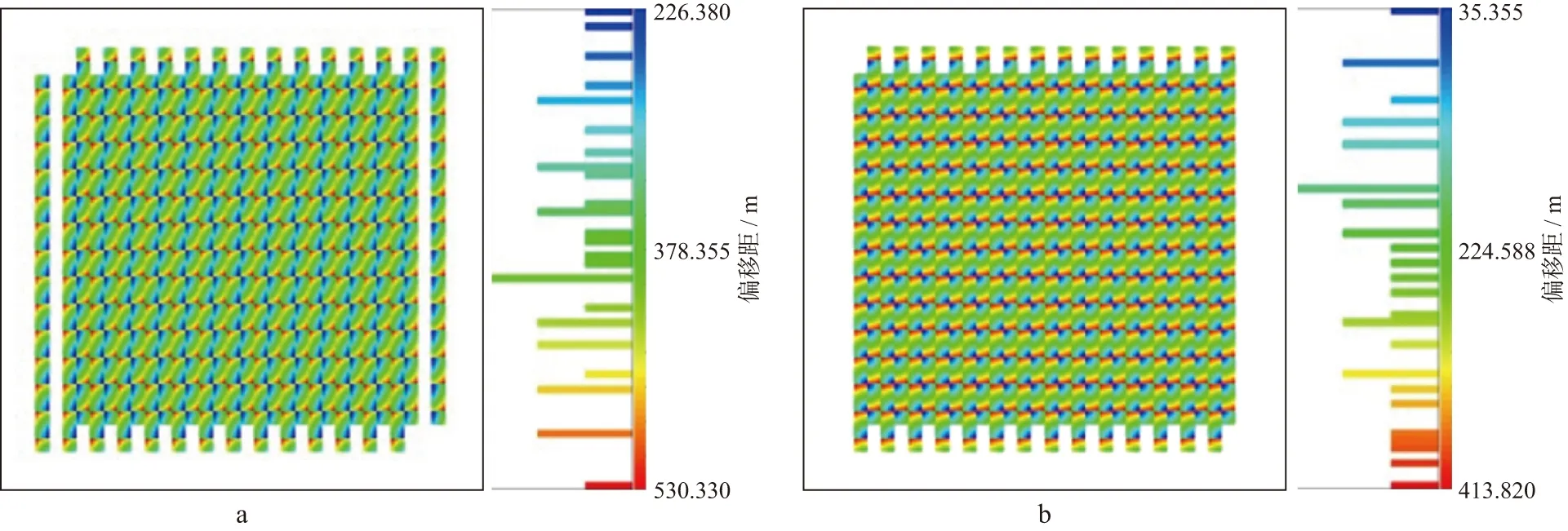
图5 两个可互换OVT片对折后分布a 第一象限; b 第三象限

2 实际应用

通常情况下,野外采集时检波线布设相对规则,所以插值的精度较炮线高,本次研究采用基于五维插值的检波线加密技术,只对检波线进行加密。研究区原始检波线距和炮线距均为360m,即OVT片尺度大小为720m×720m,通过五维插值将检波线加密一倍,使接收线距变为180m,即炮线方向尺度减小了一半,OVT片尺度变成360m×720m。从图6可以看出,经过五维插值后,检波线加密了一倍,原来布设不规则的检波线变得规则,同时检波线加密后,原来OVT片内的采集空洞得到有效弥补(图7)。

图6 插值前(a)、后(b)检波线位置

图7 插值前(a)、后(b)OVT片分布

对比加密前后的道集数据可以看出,检波线加密后道集的连续性得到提高(图8),叠加剖面连续性得到改善,信噪比得到提高(图9)。

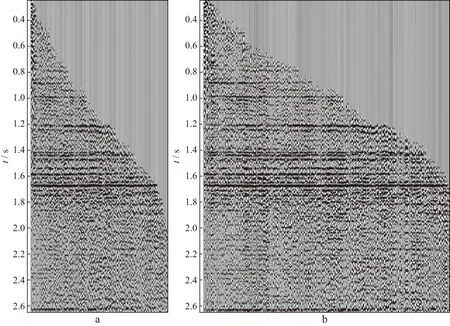
图8 五维插值前(a)、后(b)道集

图9 五维插值前(a)、后(b)叠加剖面

五维插值加密检波线后,数据覆盖次数和炮道密度都提高了一倍,但由于只加密了检波线,炮线方向的OVT片尺度减小了一半,但检波线方向的OVT处理尺度没有减小,与原数据一致,这样OVT片尺度只是从原来的720m×720m变成了360m×720m,原始正方形的OVT处理尺度变成了长方形的处理单元,这对OVT域处理不利。

所以在OVT片划分阶段,采用基于互换原理的对折法OVT片优化技术,再将检波线方向的OVT片尺度减小一半,最终实现将OVT片尺度从720m×720m减小到360m×360m的目的,从而减小OVT道集内偏移距和方位角范围,提高OVT域处理效果。

以图10中两个可互换的OVT片为例,基于互换原理的对折法OVT片优化技术具体实现过程如下:先将图10a和图10b数据分别进行复制,并将复制后的数据进行炮检点坐标互换,然后与原来的数据叠加在一起,舍去第三象限的OVT片数据,只保留第一象限的OVT片数据,再沿OVT片中心线顺着检波线(炮线)方向对保留的第一象限OVT片进行对折,从而将检波线(炮线)方向的尺度减少一半(图11)。可以看出,对折前后原始数据既没有增加,也没有减少,只是将OVT片数据进行了重新划分,这样对折后OVT片内偏移距范围和方位角范围均得到有效减小,从对折前后OVT片记录(图12)可以看出,对折后一定程度上减小了OVT片缺口,这主要是因为相互对折的两个OVT片数据缺口位置不一致,对折后两者具有一定的互补作用。

图10 两个可互换OVT片对折前(a)、后(b)(第一象限)

图11 两个可互换OVT片对折前(a)、后(b)(第三象限)

图12 对折前(a)、后(b)OVT片记录

OVT片的大小在理论上由数据的炮线距和检波线距决定,其大小为两倍的炮线距乘以两倍检波线距,即描述一个OVT片检波线方向的偏移距范围为两倍的炮线距,炮线方向的偏移范围为两倍的检波线距,由几何关系,一个OVT片内地震道偏移距O为:

(3)

所以一个OVT片内偏移距范围为:

(4)

方位角φ为:

(5)

所以一个OVT片内方位角范围为:

(6)

其中,Ox为检波线方向的偏移距;Oy为炮线方向的偏移距;Ls为炮线距;Lr为检波线距;Rmin为检波线方向最小偏移距;Rmax为检波线方向最大偏移距;Smin为炮线方位最小偏移距;Smax为炮线方向最大偏移距。

采用基于五维插值的检波线加密技术将炮线方向的尺寸减小一半(720m变为360m),然后在OVT片划分阶段,基于OVT域数据的互换原理,采用对折法优化OVT片划分,将检波线方向的尺度减小一半(720m变为360m),根据公式(4)可以计算出,原来一个OVT片偏移距范围为720m至1018m,由于OVT片尺度减小了一半,所以偏移距范围为360m至509m,从图13(α1为原始OVT片方位角范围,α2为OVT单元尺寸变小后的方位角范围)不难看出,由于OVT尺度减小了一半,单个OVT片的方位角范围得到了有效减小。

图13 OVT片单元尺寸减小前、后OVT片方位角范围

从实际资料处理前、后偏移距、方位角范围统计结果可以看出,应用减小OVT片尺度技术,使OVT片偏移距范围得到减小,平均偏移距范围从869m减小到435m(图14),处理前OVT片方位角范围为0～10°的占比21%,方位角范围为11°～20°的占比59%,处理后OVT片方位角范围为0～10°的占比增加到78%,方位角范围为11°～20°的占比减小到16%(表1)。

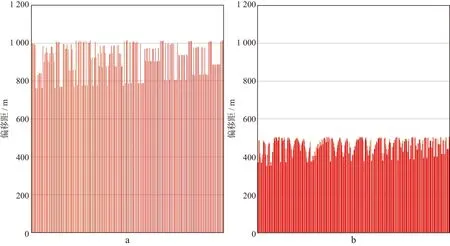
图14 处理前(a)、后(b)OVT片偏移距范围统计结果

图15为处理前、后的蜗牛道集,可以看出,采用基于五维插值的检波线加密技术加基于互换原理的对折法OVT片优化技术后,蜗牛道集的连续性和信噪比均得到有效提高,方位各向异性特征与原始道集保持一致,同时经过方位各向异性校正后,道集得到有效拉平(图16)。

图15 处理前(a)、后(b)蜗牛道集

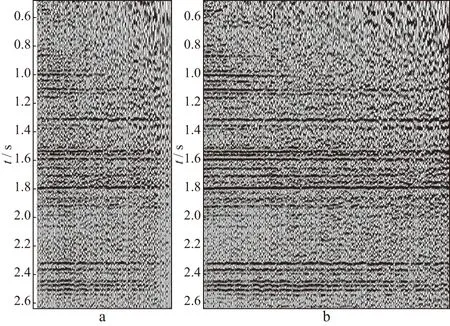
图16 处理前(a)、后(b)各向异性校正后道集

图17为处理前、后的OVT域偏移剖面,可以看出,采用基于五维插值的检波线加密技术加基于互换原理的对折法OVT片优化技术后,偏移剖面信噪比和连续性得到提高,高陡构造成像得到有效改善。同时,方位各向异性校正后方位各向异性得到更好的消除,原来由于方位各向异性引起的虚假断点得到有效校正,剖面成像更加真实(图18)。

OVT片方位角范围0～10°11°～20°21°～30°31°～40°41°～60°61°～90°处理前占比21%59%11%2%5%2%处理后占比78%16%3%1%1%1%

3 结论

OVT片的尺度取决于炮线距和检波线距,但现阶段的地震资料,其炮线距和检波线距均较大,造成OVT片的尺度较大,影响了OVT域处理效果。本文研究的减小OVT片尺度的技术,将五维插值技术和基于互换原理的对折法OVT片优化技术相结合,将原始资料的OVT片尺寸减小一倍,在实际应用过程中取得了较好的应用效果。该技术根据地震资料检波线较规则、而炮线不规则的特点,只采用加密检波线的五维插值技术,较常规五维插值既插检波线又插炮线的方式,保真性更高。而基于互换原理的对折法OVT片优化技术充分利用了OVT数据的互换性,不改变原始地震数据,只是让不同OVT片数据进行互补。通过减小OVT片尺度,增强了OVT道集偏移距和方位角的一致性,OVT域处理效果得到显著提升。

本文减小OVT片尺度的处理方法是基于原始数据炮线距等于检波线距的情况,即原始OVT处理单元为正方形,如果野外原始采集数据炮线距不等于检波线距,则需要慎重使用,同时如果单独使用这两种方法中的一种,需要视实际资料而定,因为单纯的基于五维插值加密检波线的方法只改变了OVT炮线方向的尺度,基于互换原理的对折法OVT片优化技术只能改变OVT检波线(炮线)方向的尺度,如果单一使用,可能会改变原始OVT道集数据的对称性,影响OVT域处理结果,具体影响还需深化研究,这也是后续作者研究的方向。