基于OVT域地震数据的叠前AVOA裂缝密度反演

魏欣伟,薛 姣,罗 霞

(1.中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营257000;2.中国地质大学(武汉)地球物理与空间信息学院,湖北武汉430074;3.地球内部多尺度成像湖北省重点实验室,湖北武汉430074)

裂缝是油气储层的储集空间和渗滤通道,非常规致密储层存在孔隙度低、非均质性强等特点,寻找有效的裂缝发育带对致密储层的勘探和开发尤为重要。由于地层上覆载荷的压实作用,储层中广泛发育中、高角度裂缝,造成了岩石的方位各向异性。通常把垂直定向排列裂缝储层等效为HTI(具有水平对称轴的横向各向同性)介质,利用地震波在HTI介质中传播的方位各向异性信息可以进行裂缝预测。

地震纵波在HTI介质中传播的方向特性表现为:对于固定偏移距,地震属性F与测线方位角φ的关系为F(φ)=A+Bcos[2(φ-φ0)],其中系数B反映了裂缝发育强度,角度φ0包含了裂缝走向信息[1]。RÜGER等[2]在HTI介质线性近似反射系数研究的基础上,提出利用AVO(反射振幅随偏移距变化)梯度、动校正(NMO)速度和横波分裂分析计算裂缝走向和各向异性参数。对裂缝方位各向异性比较敏感的地震属性有NMO速度[2]、反射振幅[3]、纵波旅行时[4]、频率和衰减[5]等。国内的多个碳酸盐岩、火山岩裂缝储层综合分析实例证明了利用P波地震属性随方位角变化的椭圆拟合方法进行裂缝检测的有效性[6-8]。宋维琪等[9]利用傅里叶级数形式的P波方位各向异性反射系数拟合进行裂缝各向异性估计,进一步提高了裂缝检测的准确性。

随着裂缝等效介质模型各向异性理论研究的发展,以及宽方位地震采集和处理技术研究的深入,基于AVOA数据反演裂缝参数成为裂缝储层预测研究的重点之一。AVOA裂缝参数反演中常用的裂缝等效介质模型是Schoenberg线性滑动模型[10],利用法向和切向裂缝弱度来表征裂缝,具有类似于HTI介质的弹性刚度矩阵形式。SHAW等[11]基于线性滑动裂缝等效介质模型推导了反射系数与裂缝弱度之间的关系,提出利用AVOA数据反演法向和切向裂缝弱度的方法。基于裂缝介质岩石物理模型,利用叠前地震数据AVOA进行裂缝参数反演能够充分利用叠前方位地震信息,获得裂缝等效介质模型参数,实现裂缝储层定量描述[12-14]。XUE等[15]提出了一种新流体因子表达式,以及方位各向异性反射振幅与法向和切向裂缝弱度的矩阵表达式,利用叠前AVOA技术反演了裂缝密度和新的流体因子。PAN等[16]和CHEN等[17]利用贝叶斯理论McMc(马尔科夫链蒙特卡洛)算法反演法向和切向裂缝弱度。

叠前AVOA数据反演在实际地震资料中的应用得益于宽方位地震数据采集和处理的发展。OVT技术[18-20]是一种有效的宽方位三维地震数据处理技术,OVT域道集具有丰富的炮检距和方位角信息,基于OVT域地震数据可以有效地实现方位各向异性分析与反演研究,提高裂缝储层预测的精度与可靠性[18]。目前,OVT域地震数据主要用于分方位地震属性椭圆拟合[7,19]或Thomsen各向异性参数反演[20]。

常规AVOA裂缝参数反演方法先反演法向和切向裂缝弱度,然后根据线性滑动模型与Hudson扁圆币状模型[21]的等价关系计算裂缝密度。本文基于含油和含气条件下的裂缝等效介质模型开展AVOA裂缝密度直接反演方法研究,建立基于OVT域叠前地震数据的AVOA裂缝密度反演技术流程,最后基于SK地区陆上勘探OVT域地震数据开展了AVOA裂缝密度反演和裂缝储层预测,以验证方法的有效性。

1 基本原理

1.1 裂缝等效介质模型

裂缝等效介质模型建立了裂缝参数与弹性参数之间的关系。最简单、最常用的裂缝等效介质模型是Schoenberg线性滑动模型,忽略裂缝的形状和结构,把裂缝当作无限薄的柔软平面,或者以线性滑动边界条件表示的弱度平面。线性滑动模型的基础是Backus平均[22-23],即裂缝介质的等效柔度矩阵等于各向同性背景介质的柔度矩阵与裂缝柔度矩阵之和。在线性滑动模型中裂缝被当作一个应力连续的位移间断面,位移间断和连续的应力之间的关系是线性的,因此称为线性滑动模型。线性滑动模型的刚度矩阵可以用岩石骨架的拉梅常数λ和μ,法向裂缝弱度ΔN和切向裂缝弱度ΔT来表示[11]:

C=Cb-(λ+2μ)·

(1)

式中:Cb是各向同性背景介质弹性刚度矩阵;g是背景介质横波与纵波速度比的平方,g=μ(λ+2μ);r=λ/(λ+2μ)。常规的HTI介质具有3个各向异性参数ε,γ和δ,其中ε和γ分别用于表征纵波和横波的方位各向异性。线性滑动模型是一种特殊的HTI介质模型,其中,切向裂缝弱度代表横波各向异性,与裂缝密度呈正比,法向裂缝弱度代表纵波各向异性,与裂缝密度呈正比,同时也与流体充填情况有关,当裂缝中饱和流体且流体无法流动时,法向裂缝弱度为零。

为了更加直观地表征裂缝发育程度,引入Hudson扁圆币状裂缝介质模型[21]。Hudson模型假设各向同性弹性介质中嵌入稀疏定向排列的扁圆币状(或称扁椭球状)裂缝,模拟的是超声波实验室条件下饱和岩石的性质[24],裂缝密度e可以表示为:

(2)

式中:N/V表示单位体积内的裂缝个数;a是裂缝半径(即椭球长轴半径);φ是扁圆币状裂缝孔隙度;α是裂缝扁度(即椭球短轴与长轴之间的比值)。Hudson模型的一阶等效弹性刚度矩阵为[23]:

(3)

式中:U11和U33是与裂缝性质有关的无量纲常量。线性滑动模型与Hudson扁圆币状裂缝模型对裂缝的描述有很大差别,但是又存在等价性。线性滑动模型的弹性刚度矩阵与扁圆币状裂缝介质模型的一阶近似具有相同的形式[23]。

(4)

对于流体充填裂缝,流体剪切模量μf=0,切向裂缝弱度简化为[23]:

(5)

特别地,当裂缝中饱含油、水时,流体体积模量Kf≠0,裂缝的扁度α→0,法向裂缝弱度为[23]:

ΔN=0

(6)

对于含气裂缝介质,流体体积模量Kf=0,法向裂缝弱度简化为[23]:

(7)

垂直定向排列裂缝造成了岩石性质的各向异性,利用常规椭圆拟合方法得到的椭圆扁率是一种定性的裂缝发育强度表示方法,基于裂缝岩石物理模型进行裂缝密度和裂缝弱度反演则是一种定量裂缝参数反演方法。切向裂缝弱度与裂缝密度呈正相关关系,法向裂缝弱度与裂缝密度呈正相关,与充填流体的体积模量呈负相关关系。

1.2 裂缝介质反射系数

裂缝等效介质分界面PP波反射系数可以分为与反射界面两侧各向同性背景介质物性差异有关的反射系数各向同性部分Riso(θ)以及与定向排列裂缝有关的反射系数各向异性部分Rani(θ,φ)[14]:

RPP(θ,φ)=Riso(θ)+Rani(θ,φ)

(8a)

(8b)

Rani(θ,φ)=-[g(1-2g)cos2(φ-φ0)sin2θ(1+tan2θ)+g2cos4(φ-φ0)sin2θtan2θ]δΔN+gcos2(φ-φ0)sin2θ[1-sin2(φ-φ0)tan2θ]δΔT

(8c)

式中:θ和φ分别表示入射角和测线方位角;φ0表示裂缝对称轴方向;vP是纵波速度;Z和G分别表示纵波阻抗和横波模量;符号“-”和δ分别表示反射界面两侧参数的平均值和差值,例如δΔN=ΔN2-ΔN1。当入射角θ<30°时,忽略高阶项sin2θtan2θ,则有:

(9a)

Rani(θ,φ)=-g(1-2g)cos2(φ-φ0)·sin2θδΔN+gcos2(φ-φ0)sin2θδΔT

(9b)

对于含油裂缝介质,法向裂缝弱度ΔN=0,反射系数公式简化为:

(10)

对于含气裂缝介质,根据法向裂缝弱度与裂缝密度之间的关系(公式(7)),反射系数公式简化为:

(11)

1.3 裂缝参数AVOA反演原理

假设已知裂缝对称轴方向φ0,两个不同测线方位φ1和φ2的反射系数之差为:

ΔR(θ)=R(θ,φ2)-R(θ,φ1)=Ce(θ)Δe

(12)

对于含油裂缝,模型参数正演系数为:

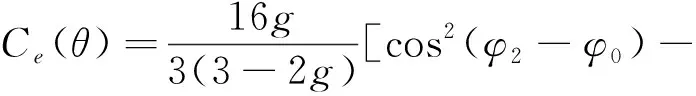
(13)

对于含气裂缝,模型参数正演系数为:

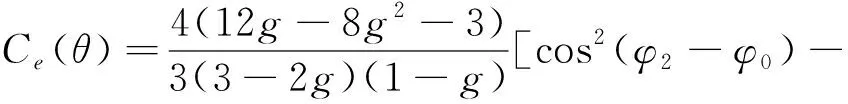
(14)

对于K+1层裂缝介质,引入地震子波矩阵,将N个入射角不同方位的地震道集差值ΔS=S(φ2)-S(φ1)与裂缝参数之间的关系表示成矩阵的形式:

(15)

式中:S(θi)=[S(θi,t1)S(θi,t2)S(θi,tK)]T表示第i个入射角对应的地震数据;W(θi)是子波褶积矩阵;Ce(θi)是由裂缝参数正演系数组成的对角矩阵:

Ce(θi)=

(16)

假设已知裂缝走向φ0,对于含油裂缝介质,利用公式(13)计算Ce(θi)矩阵对角线上的正演系数;对于含气裂缝,利用公式(14)计算Ce(θi)矩阵对角线上的正演系数。正演方程(公式(15))是一个线性方程,可以简写为:

d=Gm

(17)

式中:G是由子波矩阵,模型参数正演系数矩阵和一阶差分算子组成的线性正演算子;m=[e(t0),e(t1),,e(tK)]T表示裂缝密度向量。

假设地震数据噪声相互独立且满足高斯分布,具有相同的方差,数据的似然函数也满足高斯分布,将数据似然函数与模型先验分布结合起来得到后验概率分布,将后验概率最大化,得到目标函数:

J(m)=(d-Gm)T(d-Gm)+μR(m)

(18)

式中:R(m)是由模型参数先验分布得到的正则化项,通过改变系数μ改变模型约束条件在反演求解过程中占的比重。目标函数对模型参数m的导数为0即可求得目标函数的最小值,得到反演问题的解。本文采用Tikhonov正则化,并加入非负约束进行迭代反演。

1.4 基于OVT域数据的AVOA反演流程

常规AVAZ(振幅随方位角变化)分析或裂缝介质各向异性椭圆拟合方法中,通常通过定义叠加量版,对OVT道集数据部分偏移距、部分方位角进行叠加,从而进一步提高数据信噪比。而在AVOA反演中,需要利用偏移速度从OVT道集中抽取分方位-入射角道集,即从偏移距转换到(入射角)角度域,加强振幅能量和稳定性。

AVOA反演利用的是相同反射点的振幅随方位角和入射角的变化,而叠前道集中可能存在方位各向异性时差,以及远偏移距数据仍然存在动校正未校平的残余时差。方位各向异性和动校正误差引起的方位时差会影响反演结果的准确性,因此,需要进一步对AVOA道集做时差校正。利用滑动时窗波形匹配剩余时差校正技术,将叠后数据作为参考道,选定时窗内某一道集的所有道与参考道进行互相关,求取每道最大相关系数对应的时移量用于时差校正。

AVOA反演中需要已知裂缝走向或裂缝对称轴方向,首先利用井信息或者地震数据的椭圆拟合或AVAZ反演获取裂缝走向,继而进行AVOA裂缝参数反演[15-16,25-26]。

基于OVT道集数据的AVOA裂缝参数反演的流程如图1所示。

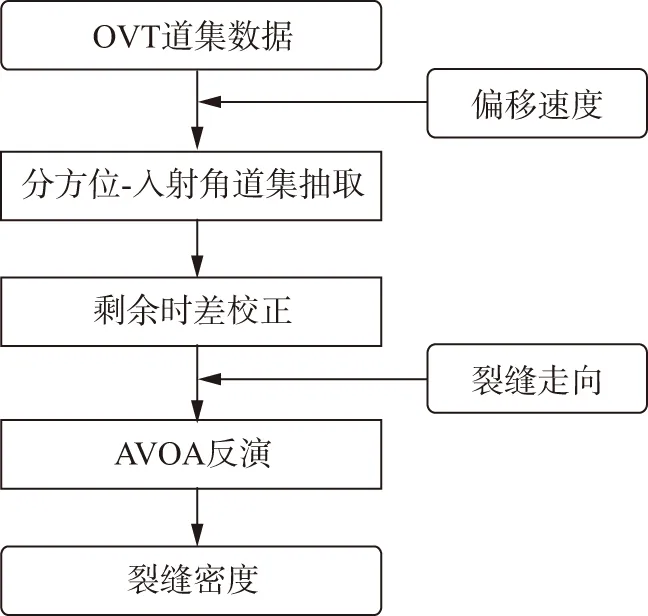
图1 基于OVT数据的AVOA反演流程

2 模型试算

建立裂缝等效介质模型,其中各向同性背景介质纵横波速度、密度和裂缝密度参数分别为R1,R2和R3,如图2所示。该模型中存在3段裂缝储层,裂缝走向为北东向45°,裂缝密度均为0.1。假设裂缝扁度α=10-6,法向裂缝弱度随充填流体体积模量的增大而减小(图3),当裂缝中充填油或水时可忽略法向弱度,切向裂缝弱度不随充填流体变化。

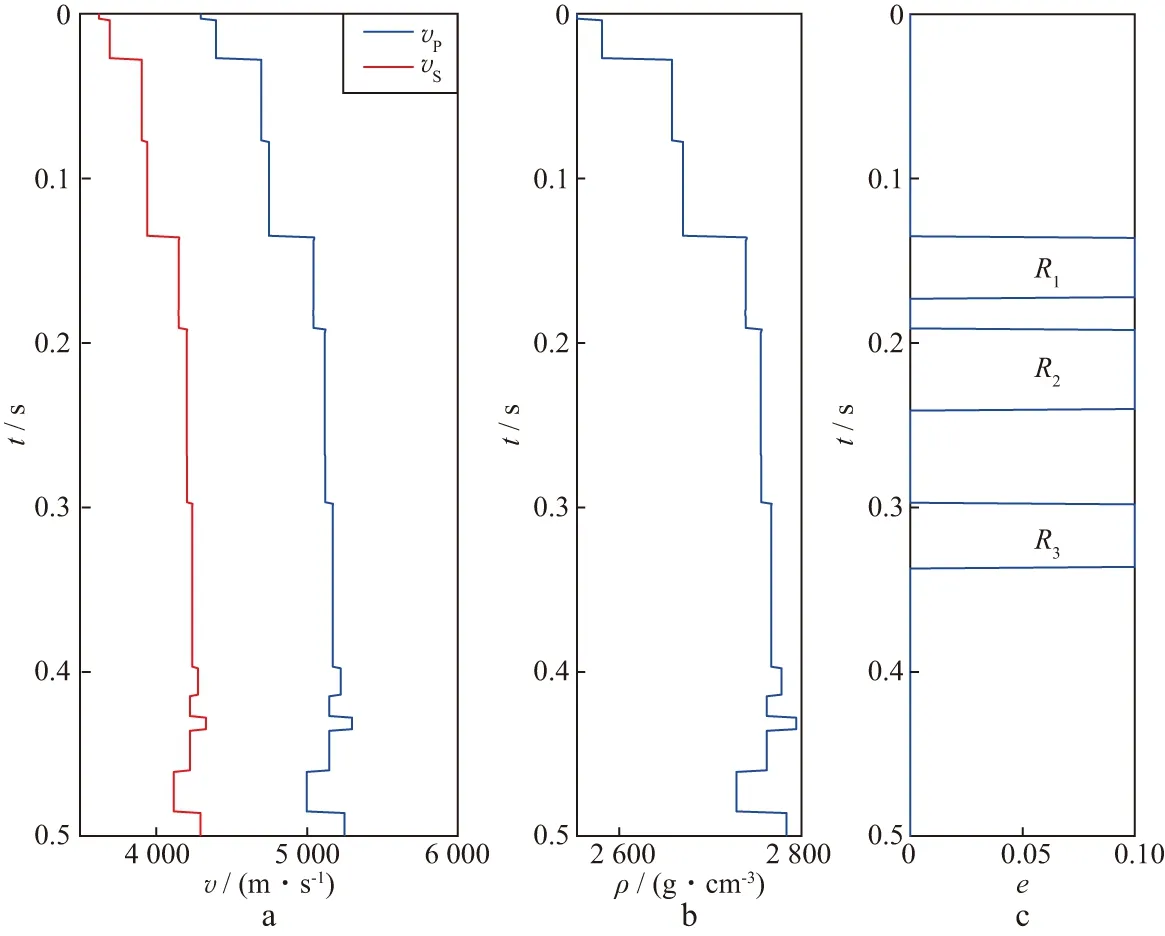
图2 裂缝介质模型纵横波速度(a)、密度(b)和裂缝密度(c)

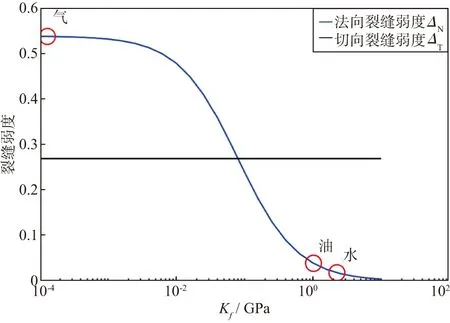
图3 裂缝弱度随充填物体积模量的变化(红圈表示含气、含油和含水裂缝介质的法向裂缝弱度)

利用本文提出的AVOA裂缝密度反演算法对裂缝储层模型的合成地震记录进行试算。假设裂缝储层中饱和充填油,利用Zoeppritz方程计算反射系数,并将反射系数与30Hz雷克子波进行褶积得到合成叠前地震记录,然后分别添加20%,50%和100%的随机噪声,得到的合成地震记录信噪比分别为RS/N=5,RS/N=2和RS/N=1。首先,对合成叠前地震数据进行AVAZ裂缝走向反演,图4显示,当信噪比大于等于2时,储层段裂缝走向反演结果与裂缝模型走向相吻合,非裂缝储层段(裂缝密度为0的位置)裂缝走向反演受噪声影响较大。利用与裂缝对称轴夹角分别为0和90°的叠前地震数据(图5和图6)进行AVOA裂缝密度反演,其结果如图7所示。由于裂缝密度不可能是负值,因此在反演过程中加入非负约束条件。图7显示,当信噪比大于等于2时满足反演要求,当信噪比为1时反演结果与裂缝模型真实值有较大差异。

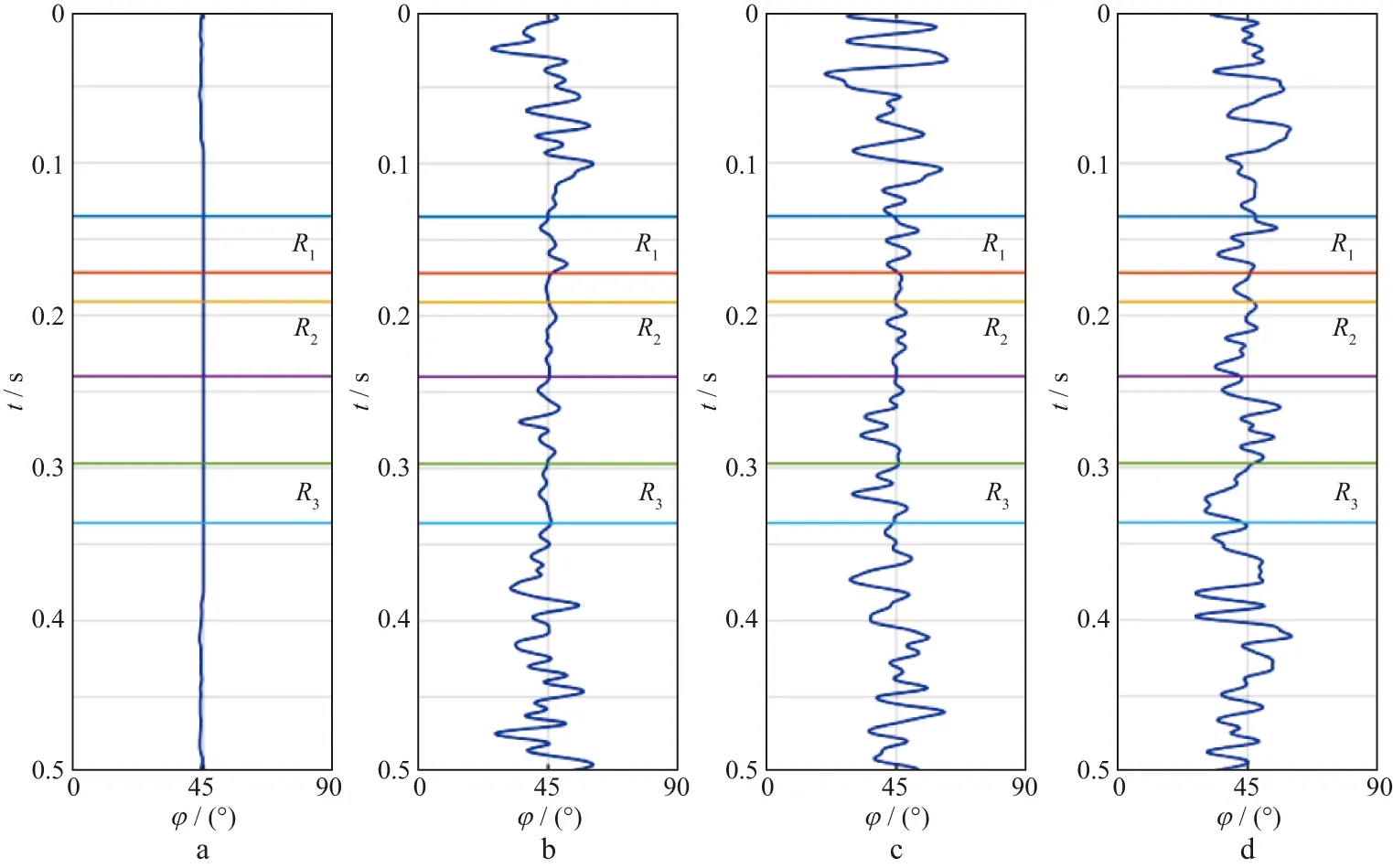
图4 不同信噪比叠前地震数据裂缝走向AVAZ反演a 不含噪声; b 含20%噪声; c 含50%噪声; d 含100%噪声

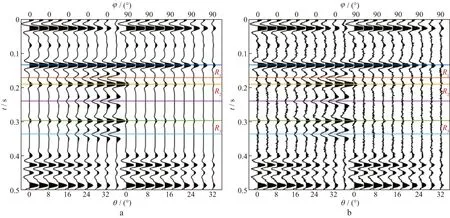
图5 不同信噪比叠前地震数据(Ⅰ)a 不含噪声; b 含20%噪声

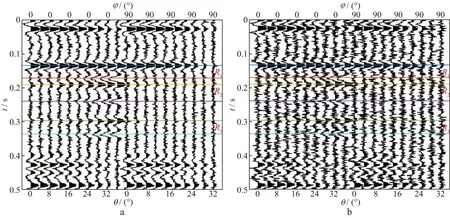
图6 不同信噪比的叠前地震数据(Ⅱ)a 含50%噪声; b 含100%噪声

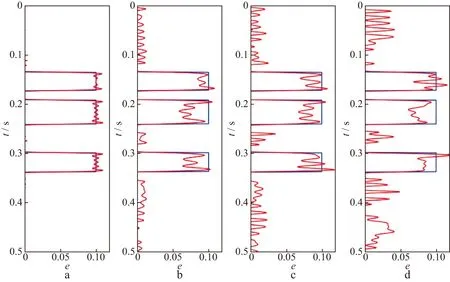
图7 不同信噪比叠前地震数据裂缝密度反演结果(红线)与模型真实值(蓝线)对比a 不含噪声; b 含20%噪声; c 含50%噪声; d 含100%噪声

假设裂缝模型为干裂缝或者含气裂缝,依然用含油情况下的AVOA裂缝密度反演方法进行反演,则其裂缝密度反演结果小于真实值(图8)。

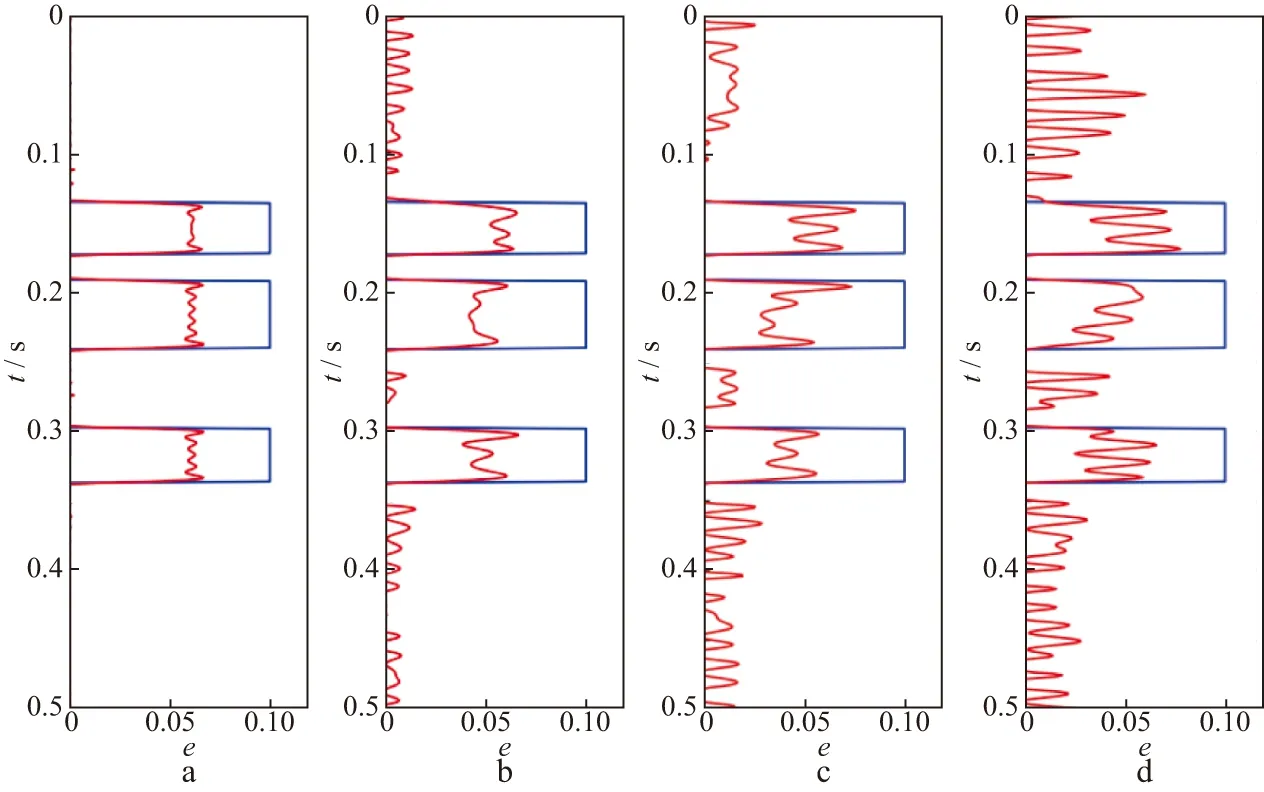
图8 干裂缝介质模型裂缝密度反演结果(红线)与模型真实值(蓝线)对比a 不含噪声; b 含20%噪声; c 含50%噪声; d 含100%噪声

3 实际应用

中国中东部某探区致密砂岩油气资源潜力大,岩性致密、基质孔隙结构复杂,具有较强的非均质性,裂缝的发育程度对致密砂岩储层的控制作用非常明显,该探区中SK工区多层系含油,裂缝较为发育,某些井试油日产达百吨以上。实际地震数据为SK工区陆上勘探得到的OVT道集。

3.1 OVT道集分析与预处理

SK工区OVT道集覆盖次数为93～312次,不同位置覆盖次数分布不均匀。方位角-偏移距变化关系分析图(图9)显示OVT道集偏移距范围为300～6000m,南北方向炮检距分布均匀,覆盖次数较高,然而横纵比较小,方位分布不均匀;南北方向最大偏移距达6000m,而东西方向最大偏移距不足2500m,东西方向远偏移距信息缺失。偏移距大于2500m的部分,方位角主要分布在0～60°和120°～180°之间,如果使用偏移距大于2500m的叠前地震数据进行AVOA反演则会产生较大误差。经过分析,有效的偏移距范围是300～2500m,其覆盖次数和方位角分布较为均衡。

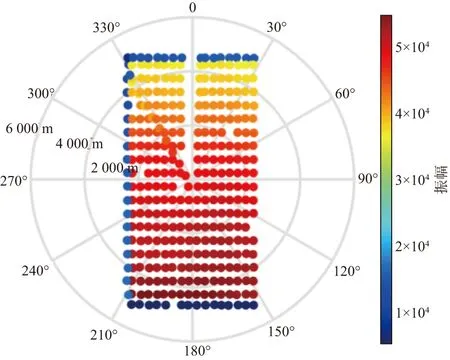
图9 方位角-偏移距分析

对OVT数据进行分方位-入射角道集抽取时,需要考虑各面元覆盖次数以及方位角和入射角个数之间的平衡。理论上讲,方位角和入射角个数越多,反演的精度越高,但随着方位角和入射角的增多,覆盖次数变少,AVOA道集数据的信噪比逐渐降低。

虽然目的层T6和T7界面最大入射角约为50°,但由于不同方位炮检距分布不均,在抽取分方位-入射角道集时应充分考虑最大有效炮检距(2500m)对应的入射角作为最大入射角(约30°)。经过试验最终确定划分为4个方位和3个入射角,生成中心方位角分别为22.5°,67.5°,112.5°和157.5°,中心入射角分别为10°,17°和24°的分方位-入射角道集(图10a)。方位角划分范围分别为0～45°,45°～90°,90°～135°和135°～180°,入射角划分范围分别为6°～13°,13°～20°,和20°～27°。选用合适的滑动时窗参数进行剩余时差校正后(图10b),方位各向异性和动校正误差引起的时差被校正,同相轴被拉平。

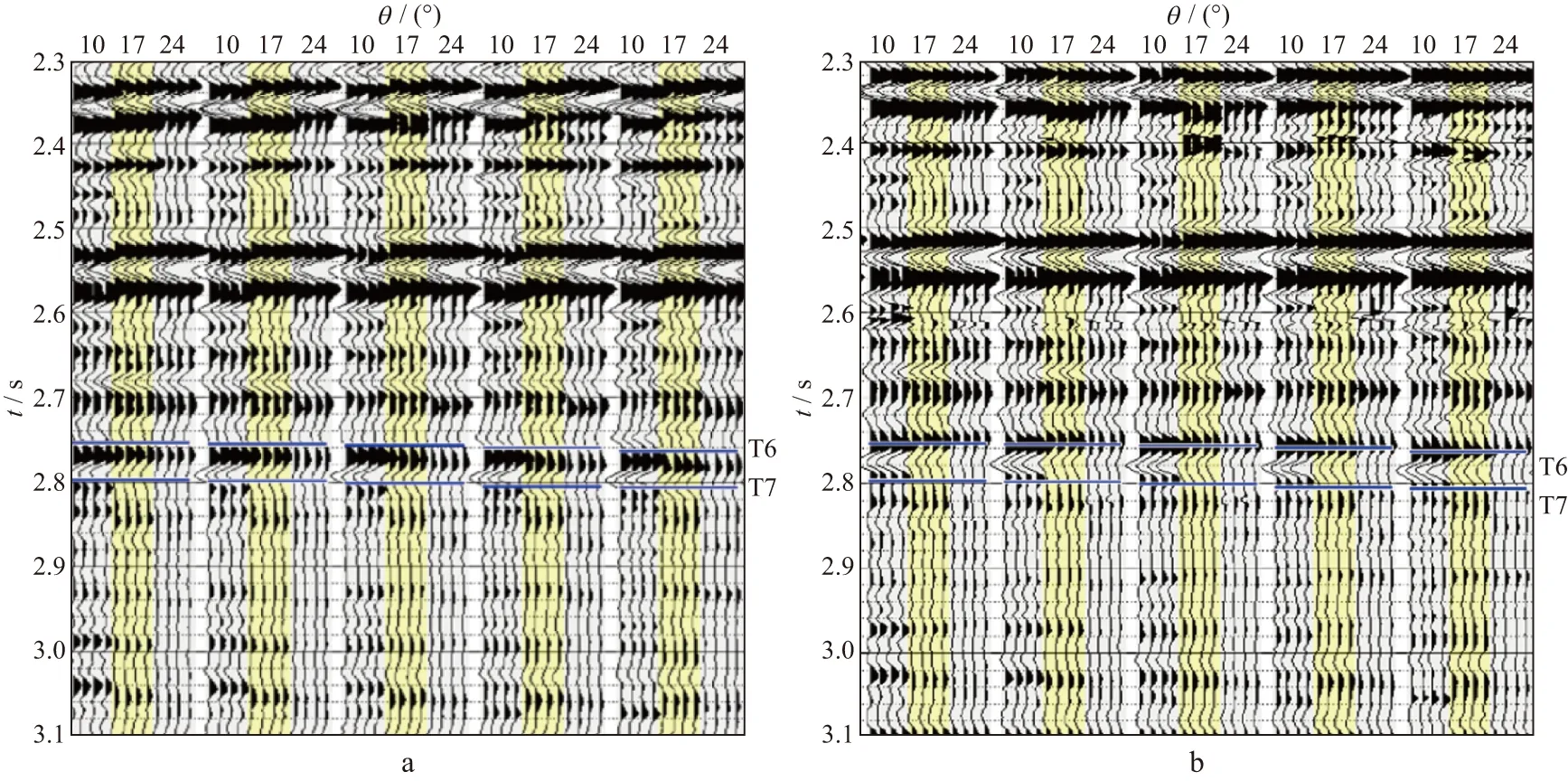
图10 时差校正前(a)、后(b)分方位-入射角道集

3.2 AVOA裂缝参数反演结果

在叠前OVT道集资料分析的基础上,抽取分方

位-入射角道集,利用滑动时窗波形匹配时差校正技术消除方位各向异性和动校正剩余时差,然后求取相互垂直的角道集之差:

(19)

式中:S(θi,φj)表示第i个入射角、第j个方位角对应的地震道;对于SK实际地震数据,S(θi,φ3)-S(θi,φ1)表示入射角为θi时第3个方位(φ3=112.5°)与第1个方位(φ1=22.5°)地震道之间的差异。首先,利用AVAZ反演估计裂缝走向,图11显示研究区目的层(T6上10ms到T6下10ms)裂缝走向主要为近东西向,裂缝走向与断裂带的延展方向一致。然后,应用本文提出的AVOA裂缝参数反演方法估计裂缝密度,达到裂缝储层预测的目的。测井、钻井、岩心和试油资料表明SK工区多层系含油,为裂缝型含油致密砂岩储层,因此将含油裂缝的模型参数正演系数(公式(13))代入模型正演方程(公式(15))中,然后利用目标函数(公式(18))最小化进行AVOA反演计算。裂缝密度沿T6层切片(图12)显示在研究区西北部yi177井到yi178井之间裂缝密度较大,为裂缝发育带。裂缝的分布主要受断裂带控制,裂缝的分布与断裂系统的分布具有一定相关性,裂缝密度较大的位置位于断裂带周围和断裂带交会处。

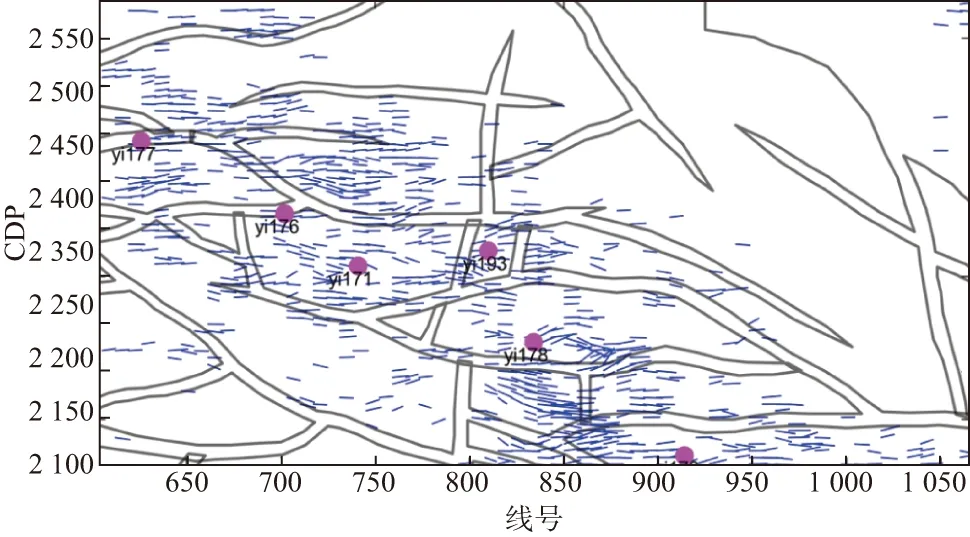
图11 沿T6层裂缝走向切片(蓝线走向表示裂缝走向,蓝线长度表示各向异性程度)

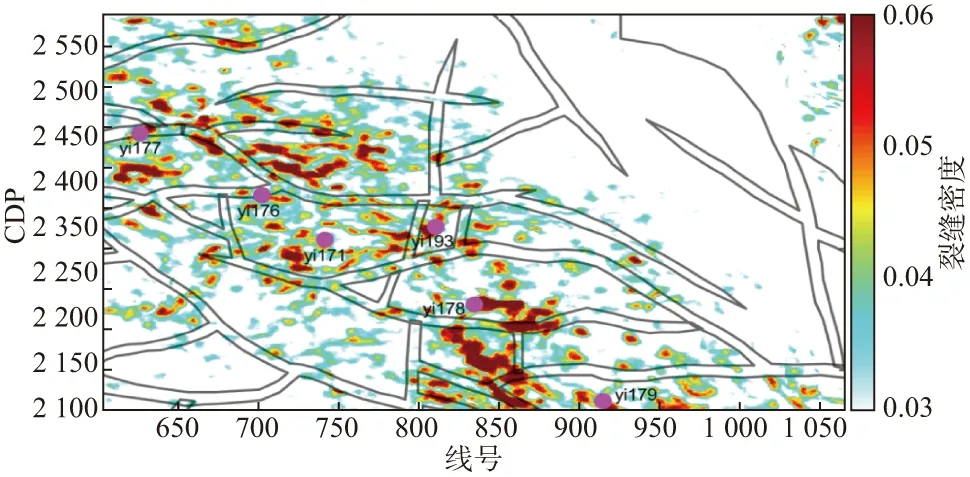
图12 沿T6层裂缝密度切片

将测井资料解释成果与AVOA裂缝密度反演结果进行对比分析,验证基于AVOA裂缝密度反演的裂缝储层预测效果。yi176井T6～T7含油层段为粉细砂岩,综合解释为油层,常规测井曲线上具有“高声波时差、高中子、低电阻、低密度和自然电位负异常”的特征。图13是过yi176井(线号702)裂缝密度反演剖面,其中,粉紫色曲线显示了正交多极子声波阵列测井得到的各向异性参数,黑色曲线是井旁地震道的裂缝密度反演结果。井旁地震道的裂缝密度反演结果(黑色曲线)与声波阵列各向异性(粉紫色曲线)异常相吻合,裂缝密度反演结果显示在T6到T7层中间及T7层上部裂缝较为发育,测井解释为裂缝储层。裂缝密度反演结果显示裂缝储层在横向上呈似层状和团块状分布。

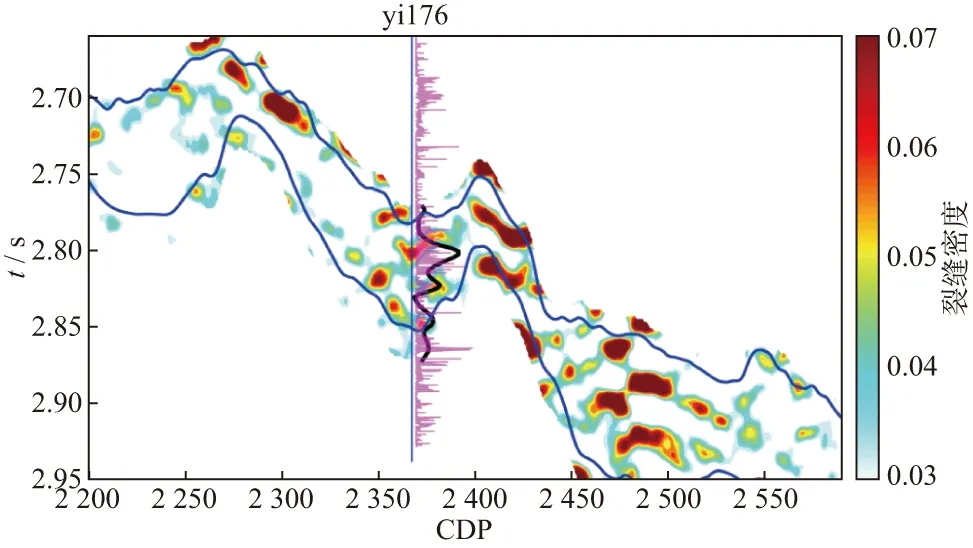
图13 过yi176井裂缝密度剖面

4 结论

本文基于裂缝等效介质模型,分别推导了含油和含气情况下反射系数与裂缝密度之间的关系,在此基础上提出了基于叠前AVOA反演的裂缝密度估计方法和基于OVT域叠前数据的裂缝密度反演技术流程。SK工区裂缝参数反演结果与测井资料解释成果相吻合,显示了OVT域AVOA裂缝参数反演的有效性及其在SK工区裂缝储层预测中的适用性。基于OVT域地震数据的AVOA裂缝参数反演结果能够定量刻画裂缝分布特征,为SK工区致密砂岩含油裂缝储层预测和开发提供了重要依据。