基于硅-焓混合模型的热储温度估算方法

2021-09-28宋利红李海福孙晗森郑丽婧徐春阳

天然气勘探与开发 2021年3期

宋利红杨宇李海福孙晗森郑丽婧徐春阳

1. 成都理工大学能源学院 2. 中海油研究总院有限责任公司 3. 中国石油辽河油田公司勘探开发研究院

0 引言

地热储层温度的确定在地热资源的开发评价过程中有着举足轻重的地位，众多学者[1-4]针对不同地区利用阳离子Na-K温标、K-Mg温标、Na-K-Ca温标、Na-K-Mg温标等对热储温度进行了计算。但地热储层温度通常会受到很多因素的影响：不同储层的地热流体可能在采出前发生混合，对流体温度进行分析时存在一定的误差；相邻层段的层间窜流、循环对流等会使地热流体在开采前就与其他液体发生混合，从而影响储层温度的测量。特别是地面冷水与热流体的混合会使大量的Cl-、Na+、K+等离子混入，这些离子之间的比值会大大影响地热温标方法计算的准确性。因此，针对这种情况，常常利用混合模型计算热储层温度、分析地下热流体深部温度特征和冷热水混合过程[5]。

在1974年，Fournier和Truesdell根据硅-焓（即二氧化硅-水的焓值）平衡提出了混合模型并成功对储层原始流体的温度进行了估算；王晓翠[6]对云南沘江沿岸温泉水进行了水化学分析，采用硅-焓图解法对地下热水在采出前未发生蒸汽和热量损失的情况进行了热储温度计算。但前人的实践应用表明，硅-焓图解法对热储温度的计算已经广泛应用，但绘图过程繁琐。基于此，在硅-焓图解法的基础上，提出改进图解法以及Newton-Raphson迭代算法，并对热储温度进行了计算。

1 混合模型的提出

地表的大气降水通常会与地热水混合，通常的混合情况如图1所示。在C点处地下流体呈高温热水状态，并在地下渗流通道内向上流动，在某个深度与向下渗流的地表大气降水（A点）混合，即“混合点（D点）”。随后产生温泉水，在地表显露（B点）。图1中显示，若在该区打井钻至C处，采出液将全为地下热流体，该处可采用传统的地质温度计直接计算热流体温度。如果钻遇到地表水和地热水的混合液，其混合液的温度并不能表征地下的热储温度，采用传统的地质温度计无法准确得出热流体温度，必须采用混合模型方法进行计算[7]。

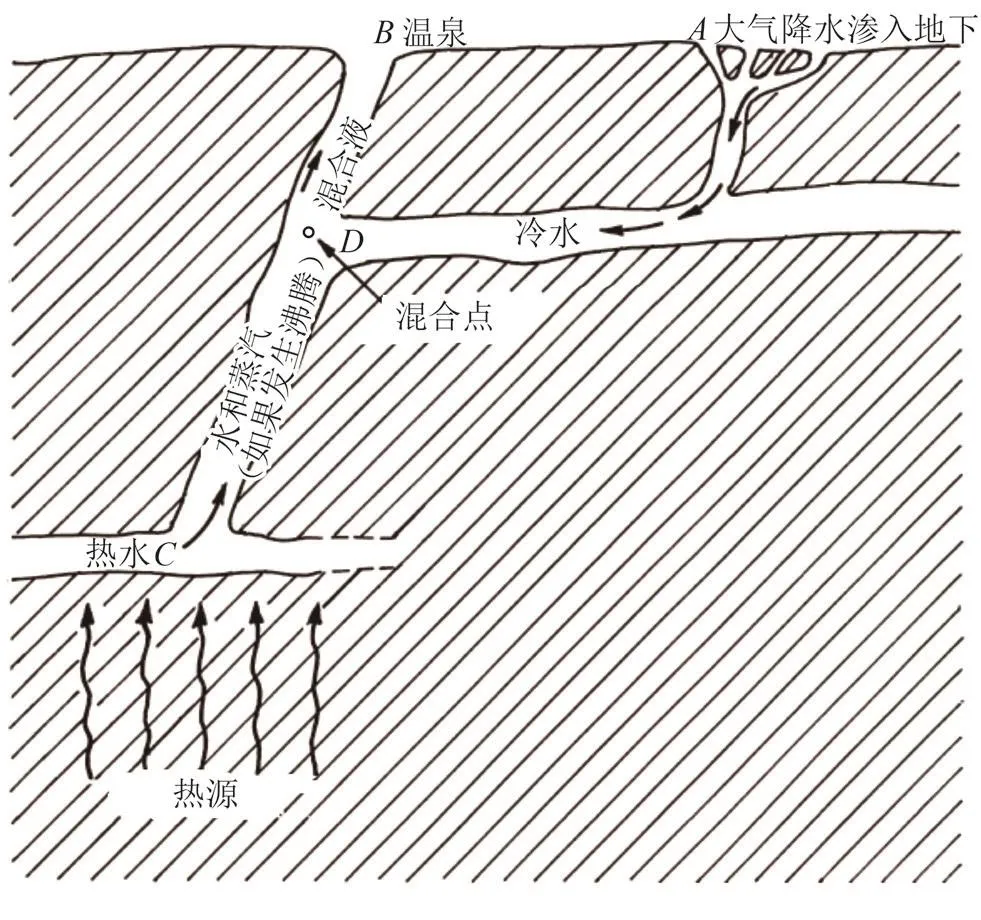
图1 地热流体与冷水混合示意图[9]

混合模型方法是通过对温泉水以及该地区的冷水温度、二氧化硅含量进行测量，从而对混合液中热水温度及冷水比例进行估计。混合模型法通常利用图版进行求解，在绘图读数时容易产生误差[8]。基于此，为了减小绘图读数产生的误差，在方程组构建的前提下提出了改进图解法和Newton-Raphson迭代求解方法，并对热储温度进行计算。

2 混合模型计算方法

2.1 方程组的构建

Fournier和Truesdell在1974年针对图1这种典型的地热流体混合情况提出了一种计算热水温度和冷水在混合液中所占比例的方法，并得出了热水温度与焓、SiO2含量之间的关系（表1）。对此方法作了三个基本假设：一是混合后没有热量损失；二是储层流体的二氧化硅含量由石英的溶解度控制；三是不管是否发生混合，二氧化硅都不会发生沉积或溶解。由于地热水与冷水混合前发生蒸汽损失会导致计算失准，所以方程组只适用于混合前未发生蒸汽损失的情况[9]。

由能量守恒原理可知：

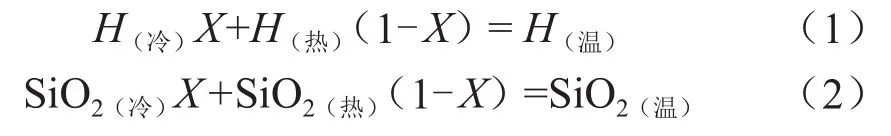
式中H（冷）表示冷水的焓，kJ/kg；H（热）表示热水的焓，kJ/kg；H（温）表示混合温泉水的焓；SiO2（冷）表示冷水的二氧化硅含量，mg/L；SiO2（热）表示热水的二氧化硅含量，mg/L；SiO2（温）表示混合温泉水的二氧化硅含量，mg/L；X表示冷水在混合液中所占的比例。

表1中的关系引自 Fournier等（1974）[9]及Gupta等（2007）[10]。利用表1数据做出二氧化硅含量和温度的关系曲线，拟合得到SiO2含量与温度的关系式：

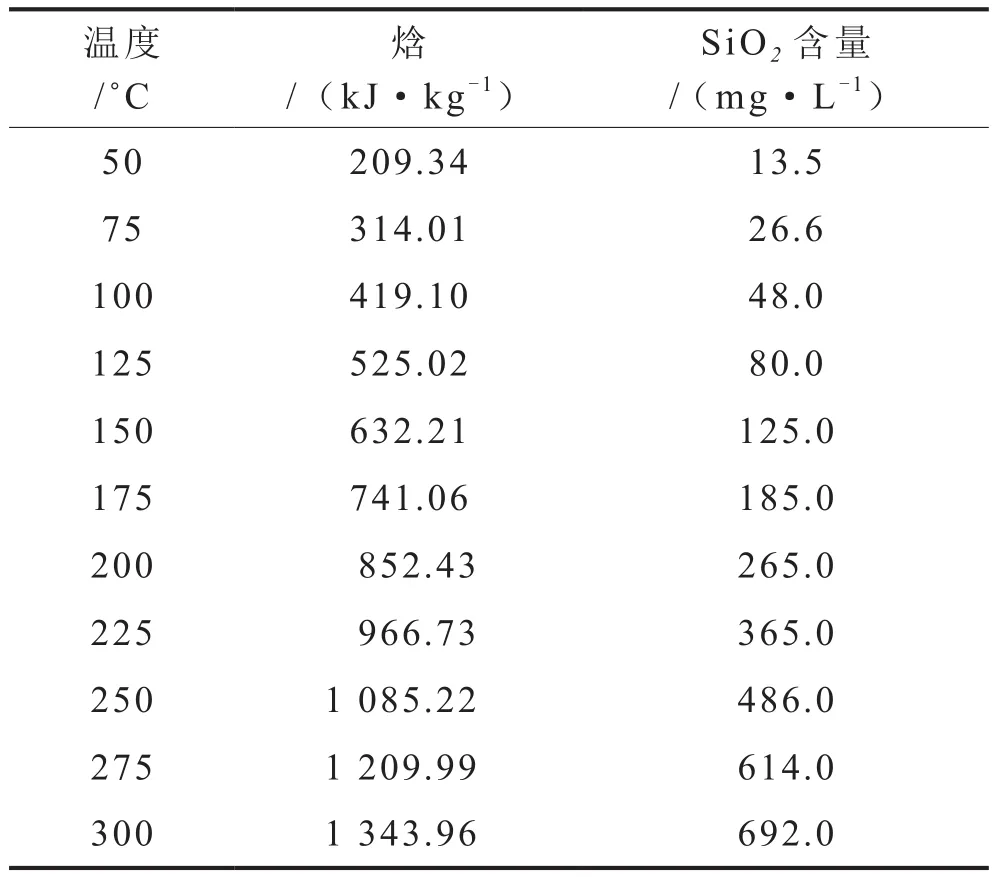
表1 热水温度、焓和SiO2含量表[9-10]

式中T表示热水温度，℃；SiO2表示二氧化硅含量，mg/L；拟合精度R=0.997。

式（1）、（2）中焓和二氧化硅都是和热水温度有关的函数。

热水温度和焓之间的关系如下[11]。

当60℃≤T≤330℃时：

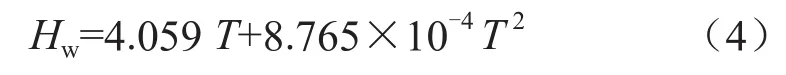
当240℃≤T≤330℃时：

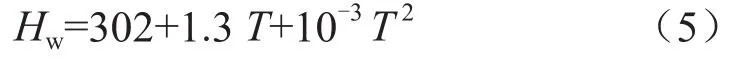
在不发生蒸汽损失情况下，联立式（1）、（2）、（3）、（4）和（5）可得出热水温度以及二氧化硅含量的表达式。

当60℃≤T≤240℃时：

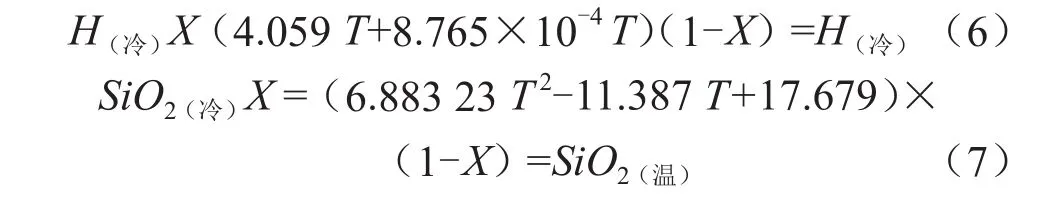
当240℃≤T≤330℃时：

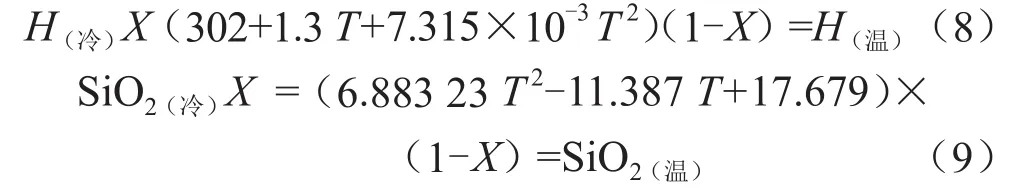
在式（6）～式（9）中，热水温度和冷水混合比例X均为未知数。在现场测得的H（温）、SiO2（温）、H（冷）、SiO2（冷）数据基础上，利用图解法、改进图解法及Newton-Raphson方法进行求解。

2.2 图解法求解

图解法是基于热焓和二氧化硅平衡的一种方法，其原理简单，容易估计混合水中热水组分的温度[12]。

由于地下热水中溶解二氧化硅的规律遵循SiO2在热水中的溶解度曲线。因此，温度越高，对应焓值越大，SiO2的溶解量也越多。而且热水在通道中上升的过程中，与冷水混合后，温度会迅速降低，但是SiO2的溶解量降低的速度会更加迟缓一些，所以这种SiO2的“滞后记忆”功能可以记录较长时间段内地下热水的温度值[13]。

因此，基于这一原理，可以利用水的温度和二氧化硅浓度在曲线上推算出原始的热储温度，具有简单、高效的优点[14]。分析步骤如下（图2）：

图2 硅-焓关系图

①确定当地大气降水的温度和二氧化硅含量；

②使用蒸汽表[15]将温度转换为焓，并在硅-焓图中绘制出大气降水的硅-焓点A；

③同理，确定热泉水的温度和二氧化硅含量；

④将温度转换为焓，并在图中绘制热泉水的硅-焓点B；

⑤通过二氧化硅在热水中的溶解量与焓的关系，来绘制没有蒸汽损失时的二氧化硅溶解度曲线；

⑥连接热泉水和大气降水的硅-焓点，并作延长线与二氧化硅溶解度曲线相交于C点，C点的对应坐标表示地下热水的焓值，通过查对应蒸汽表即可计算出对应的热储温度。由大气降水的硅-焓点与热泉水硅-焓点之间的距离AB除以大气降水的硅-焓点与上述延长线交点间的距离AC来计算出冷水的混合比例（图2）。

2.3 改进图解法求解

由于利用图解法读取C点坐标时容易产生误差，从而影响计算结果的准确性，于是将图解法进行改进，基于图2中直线AB和SiO2溶解度曲线，直接计算交点，提高计算精度。

图2中直线AB是基于混合过程能量守恒的前提下，冷水变为温水的线性变化过程，直线BC表示混合过程使热水变为温水的线性变化过程。因此，基于SiO2的“滞后记忆”功能，对图解法进行改进：利用方程解出C点的坐标值，来表征一定时间段内的热储温度，即求出直线AB与SiO2溶解度曲线的交点（C点坐标）。直线AB的方程可以通过联立式（1）和式（2）表示出来。

用x代表热水焓值H（热），y表示热水二氧化硅含量SiO2，可得出AB直线方程为：

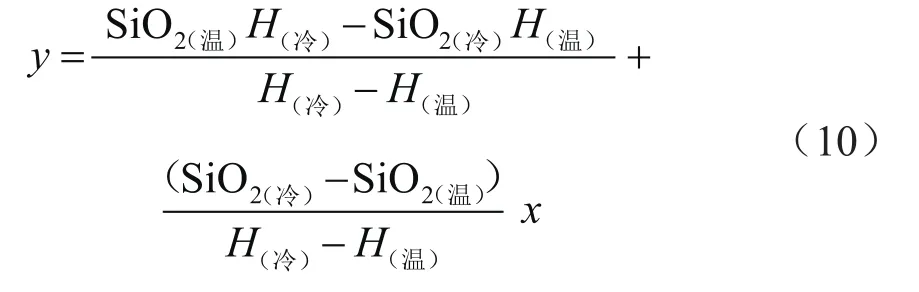
根据得出式（3）的方法，结合热水的温度焓值表，做出硅-焓关系曲线并进行拟合，拟合精度R=0.999，得到：

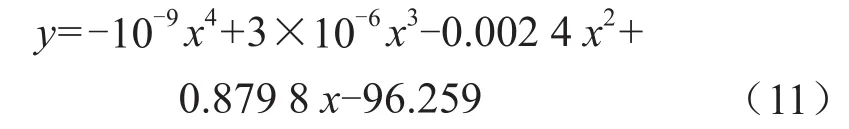
因此，联立式（10）、（11）并代入实际水样数据可直接计算出C点坐标值，即可得出热水焓值和热水二氧化硅含量。针对图解法中直接读出的C点坐标值和通过改进图解法计算出的C点坐标值，会存在一定的差异。因此，采用改进图解法计算出的结果可以校正图解法读数的误差，具有实际意义。

2.4 Newton-Raphson方法求解

除了对图解法进行改进外，提出了利用Newton-Raphson迭代法[16]来计算热储温度和冷水混合比例值。

Newton-Raphson迭代法是一种用构造的近似线性方程代替原方程的方法，常用于求解非线性方程组的近似解。从方法的构造、编程方式上讲，具有一定的普适性，是目前使用较为广泛的一种迭代求解非线性方程的方法。

对于非线性方程f（T）的根T*，设有一个近似值Tk≈T*，实值函数f（T）在零点T*的充分小邻域U（T*）内二阶连续可微且f'（T）≠0。

由泰勒展开式可得到：

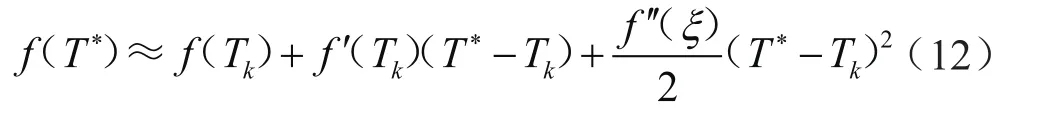
因为f（T*）=0，f'（T）≠ 0，所以有：

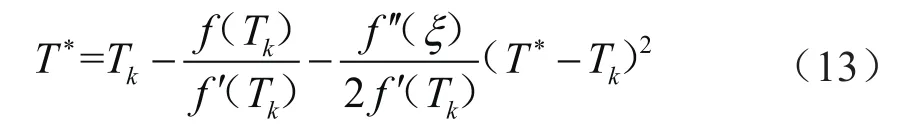
将方程（7）中右边的高阶项略去，变成一个新的近似值，记为Tk+1，由此可得到牛顿迭代公式为：

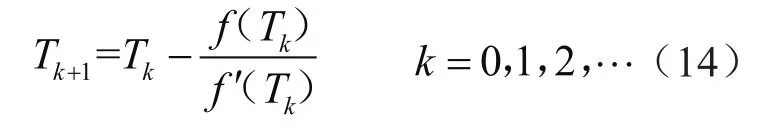
利用Newton-Raphson方法迭代求解热水温度（T）和冷水混合比例（X）的具体步骤如下。

②计算雅可比矩阵：

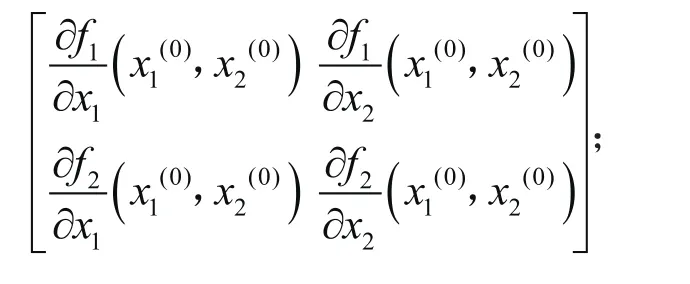
③求线性方程组的解Δx；

是：输出x，计算结束；

否：进一步判断k=N?

是：输出“已达到最大迭代次数!”；

否：x（0）=x，返回第一步进行重复计算。

3 计算实例

海阔对各区不同水样进行分析，假设地热流体与冷水混合前没有发生蒸汽损失。本次引用其文章中的五个水样数据进行相关研究，各研究区雨水的温度和二氧化硅含量在表2中给出。

根据表2中相关数据，利用图解法画出一系列如图3所示的硅-焓图，并求出对应方程与二氧化硅溶解曲线的交点值。读出对应坐标值与计算出的坐标值如表3所示。

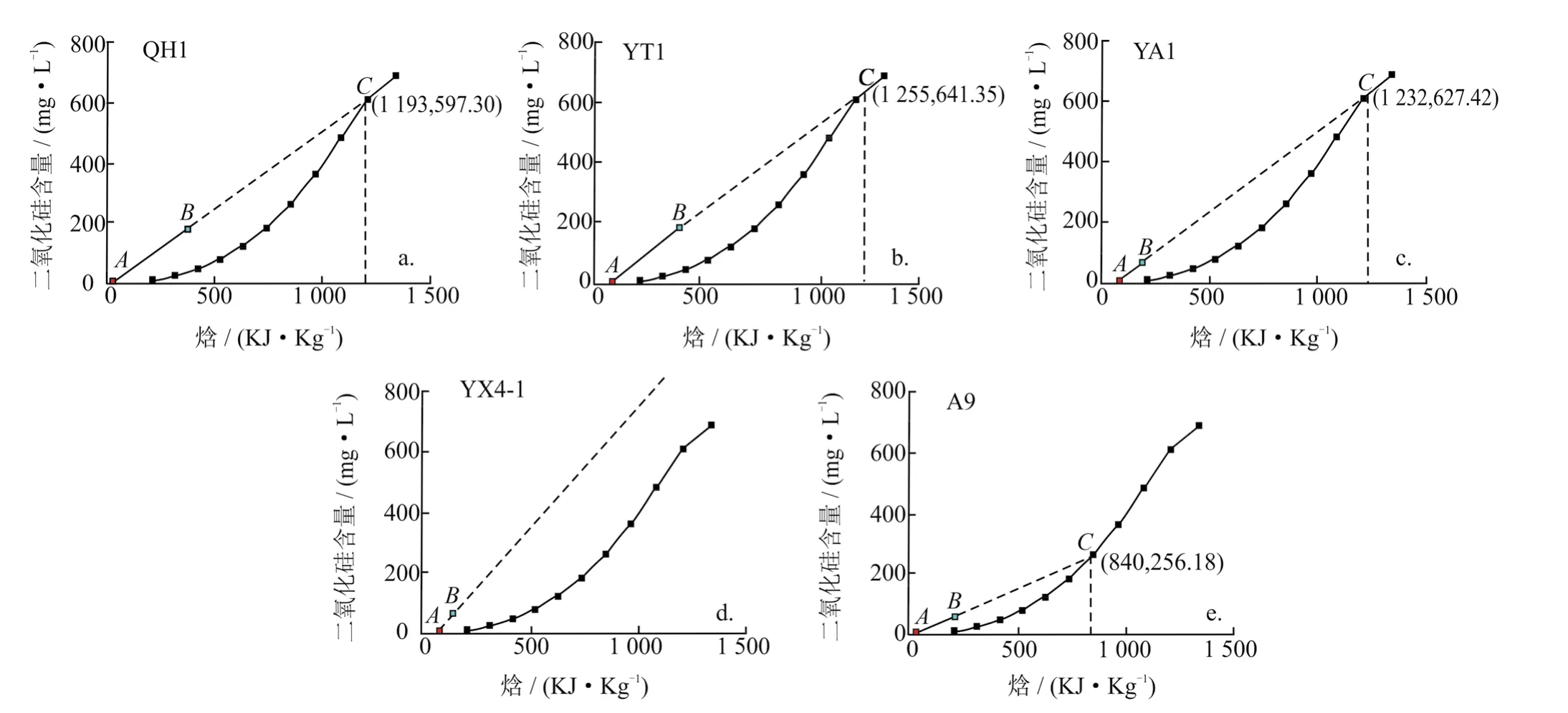
图3 混合前没有蒸汽和热量损失的硅-焓示意图

表2 部分水样数据表[20]

图中曲线表示没有发生蒸汽损失时的二氧化硅溶解度曲线。

由表3可知，C1的坐标值是通过图解法直接读数而求出的，C2坐标值是通过求解直线AB及二氧化硅溶解度曲线方程组求出的交点。二者计算结果相差不大，说明改进图解法计算热储温度的可行性。

表3 图解法和改进图解法得出的对应坐标值表

表4计算结果表明，除去水样YX4-1，利用图解法和改进图解法计算出的4个水样热水温度差值分别为2.3℃、8.0℃、2.3℃、7.0℃，求取平均值是4.90℃；图解法和Newton-Raphson方法计算出的四个水样热水温度差值分别为2.6℃、8.6℃、1.3℃、1.1℃，求取平均值是3.40℃；改进图解法和Newton-Raphson方法计算出的4个水样热水温度差值分别为0.3℃、0.6℃、1.0℃、5.9℃，求取平均值是1.95℃。