一种融合集成思想的不平衡数据分类方法

强冰冰，尹 红，王 瑞

（昆明理工大学机电工程学院，云南昆明 650550）

0 引言

在实际生产和生活中，广泛存在数据类分布不均衡现象，单一的传统分类器，如神经网络、SVM 等在处理不平衡数据时，往往倾向于多数类，使得少数类的分类效果较差。而在实际应用场景中，如医学诊断［1］、信用卡欺诈检测［2］等，少数类的正确分类具有重要意义，因此，国内外学者从数据和算法的角度对不平衡数据分类进行了研究。

针对不平衡数据在数据层面的处理，以过采样和欠采样方法为代表，通过调节样本类别的比例以达到类平衡；在算法层面，其思路是基于现有算法进行改进，使其能够更好地区分少数类，主要有单类学习［3-4］、代价敏感学习［5-6］和集成学习等。

在数据层面，过采样方法是通过增加少数类的数量以达到样本均衡。传统的随机过采样，在合成样本时具有较大的随机性和盲目性，容易使模型过拟合，于是Chawla［7］提出SMOTE 过采样技术，有效降低了过拟合的风险；SMOTE虽然简单有效，但同时也存在样本合成质量低、边界模糊和类分布不均匀问题［8-9］。为了解决上述问题，文献［10］提出基于K 均值聚类和SMOTE 相结合的K-means SMOTE过采样方法，提高了样本合成质量，克服了类分布不均匀问题，但寻找超参数的最优值往往依赖于经验；文献［11］基于CNN（Condensed Nearest Neighbor）和Tomek-link，提出了一种改进的过采样方法，可以较好地检测出离群点、噪声和冗余样本；文献［12］根据学习困难程度对少数类使用加权分布，考虑到少数类样本的分布特点，提出自适应的合成少数类样本的ADASYN 采样方法；文献［13］利用边界样本的最近邻密度剔除噪声点和确定合成样本数量，对SMOTE 方法的新样本合成规则进行了优化；文献［14］针对少数类的分布问题，采用cGAN（conditional Generative Ad⁃versarial Networks）进行过采样，这种方法虽然较好地拟合了真实数据分布，但是cGAN 具有一定的时间复杂度，并且训练一个性能较好的cGAN 需要相当的数据量；文献［15］提出将样本划分成3 个区域：正域、边界域和负域，分别对边界域和负域中的小类样本进行不同的过采样处理，提出了一种基于三支决策的不平衡数据过采样方法，但时间复杂性较大。

在算法层面，集成学习通过组合多个基分类器提高少数类样本识别率。Boosting 算法在每一轮的迭代中，会根据样本分布对训练集进行重新采样，如果样本被错误分类，权重会增加。在不平衡数据集中，少数类更容易被分错，在每次迭代时，少数类的权值会逐渐增加，在一定程度上保证了少数类能够被识别。由于Boosting 算法族在识别少数类上具有优势，因此很多研究者提出了基于Boosting算法族的改进方法以解决不平衡数据分类问题。文献［16］将欠采样和集成学习相结合，提出了Easy Ensemble 和Balance Cascade；文献［17］通过对大类中分类困难样本的权重和标签进行处理，提出基于AdaBoost 的改进算法，但存在着如何确定阈值和处理权重问题；文献［18］提出PC⁃Boost，该算法利用数据合成方法添加合成的少数类以平衡训练信息；文献［19］提出多类别不平衡学习算法，利用混合的集成技术充分挖掘被随机欠采样方法忽略的潜在有用的大类样本信息；文献［20］基于集成学习架构，将欠采样技术、Real Adaboost、代价敏感权值修正和自适应边界决策策略相结合，提出自适应的EUSBoost。

综上所述，过采样方法虽然能够在一定程度上解决不平衡数据分类问题，但是可能会引入无用的信息和噪声，导致分类算法效果下降；基于集成学习的boosting 算法族虽然在解决不平衡分类上有着较好效果，但没有考虑到样本数据分布的先验信息。针对以上问题，考虑到少数类样本较少并结合集成的思想，针对不平衡数据，本文从数据层面和算法层面出发进行研究，通过改变数据分布，使得少数类和多数类的边界更清晰，从而让算法在少数类上的表现更好。

1 基于集成思想的不平衡数据分类算法

针对不平衡数据处理，本文所提出的算法分为3 个阶段：数据处理阶段、基分类器训练阶段和原始算法训练阶段，如图1 所示。

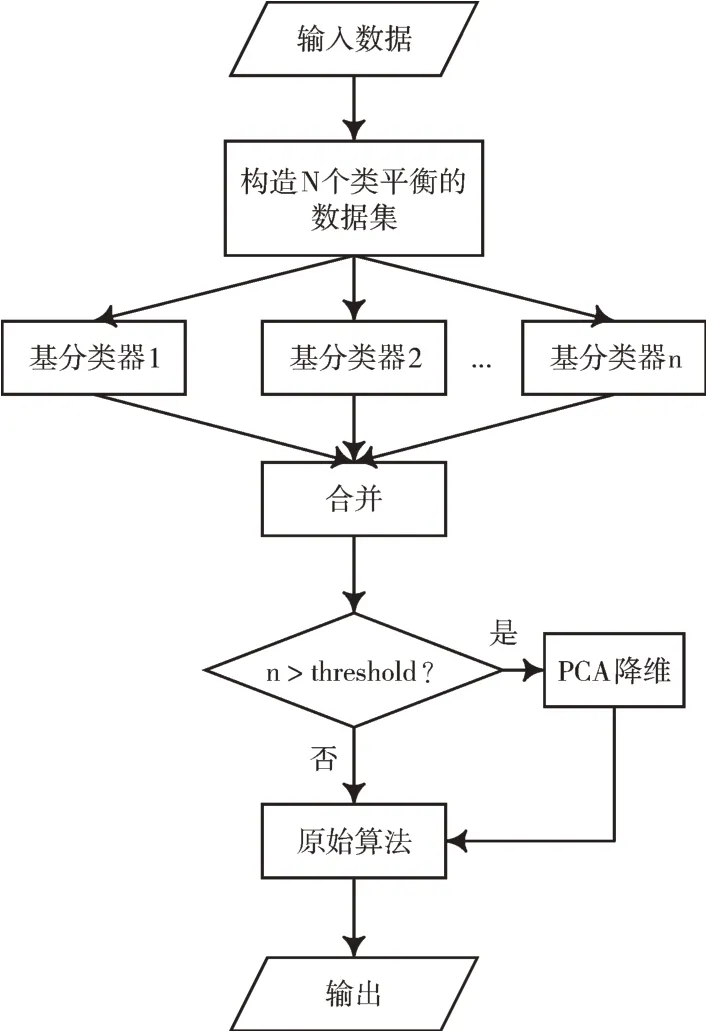
Fig.1 Imbalanced data classification model incorporating ensemble ideas图1 融合集成思想的不平衡数据分类模型

采用过采样方法合成的样本并不能够完全替代真实的样本，会引入一定的噪声；而降采样方法删除的样本可能包含有用信息，从而丢失了部分信息。避免过多引入噪声和丢失信息，在数据处理阶段利用现有数据集和Kmeans SMOTE 合成少量样本以构造多个类平衡的数据集。

相关研究表明，基分类器的差异性能够提高集成性能［21-22］，因此，在基分类器训练阶段从数据和算法的角度构造具有差异性的基分类器，以提高集成效果。

通过前两个阶段得到基分类器的输出后将其合并，为了提高算法运行效率，可以设置阈值ρ，当合并后数据的维度大于某个阈值，使用PCA 降维，再将处理后的数据作为原始算法输入。详细算法流程如图1 所示。

输入：样本D=（xi，yi），i=1，2，…，n，xi是n维特征空间的样本，yi是类标签。基学习器L=｛l1，l2，…，lk｝，lk为不同种类的基学习器。

输出：预测结果y_predi，i=1，2，…，n

（1）初始化ρ；

（2）计算少数类数量Ns，多数类数量Nl；

（3）计算需要合成的样本数：

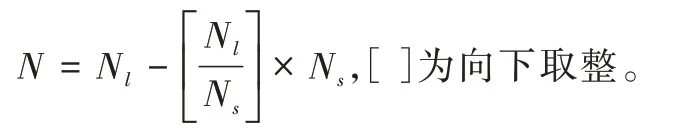
（4）使用K-means 进行聚类，将特征空间划分为K 个聚类，根据每个聚类的不平衡度选定过采样的聚类f。

（5）对于每个选定的聚类，用欧式距离计算每个少数类样本点到其他少数类样本点的距离，存放到矩阵；将矩阵的所有非对角元素相加，除以非对角元素的数量得到每个聚类的平均距离averageDistance（f）。

（6）计算每个选定聚类的密度：

density(f)=即少数类的数量除以平均距离的m的幂次方，m为特征个数。

（7）计算每个选定聚类的稀疏因子：

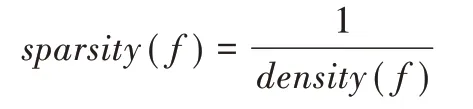
（8）每个聚类的采样权重为该聚类稀疏因子除以所有聚类稀疏因子之和。根据需要合成的样本数N和采样权重确定每个聚类合成的样本数量，再利用SMOTE 合成样本，并添加到D中。

（9）D 中少数类的样本集合为S，多数类样本集合为L。从L中随机抽取Ns个样本与S构成类平衡的集合di，i=1，2，…，k，k=

（10）集成k个种类的基学习器，得到基学习器E；

（11）forj=1：k

（12）用dj训练学习器E 得到输出fj,k

（13）end for

（14）合并L的输出得到D″=(fi,k,yi)，i=1，2，…，n；

（15）ifk>ρ

（16）使用PCA 将D″降维；

（17）end if

（18）使用D″训练原始算法得到输出y_predi。

2 实验与分析

2.1 评价方法

对于二分类问题，根据真实值和算法预测值，可以得到混淆矩阵，如表1 所示。

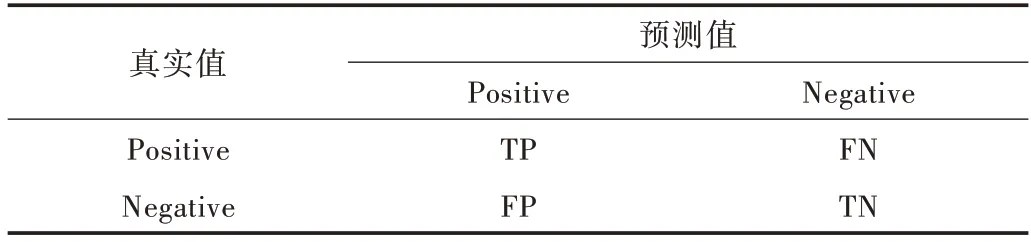
Table 1 Confusion matrix表1 混淆矩阵

为了能够评价学习器在不平衡数据上的性能，本文使用F-measure、G-mean 和AUC 指标评价学习器的表现，将少数类定义为Positive，多数类定为Negative，计算公式如下：

为了评估算法性能，利用Friedman 检验进行统计意义上的比较。Friedman 检验是利用秩实现对总体分布是否存在显著差异的非参数检验方法，步骤如下：

（1）原假设H0：每个算法性能相同；备择假设H1：至少有两个算法性能存在差异。

（2）首先使用交叉验证得到每个算法在每个测试集上的结果；然后在每个数据集上根据测试性能由好到坏进行排序，若相同，则取平均序值。

（3）假设在N个数据集上比较k个算法，令ri表示第i个算法的平均序值，则检验统计量Fr为：

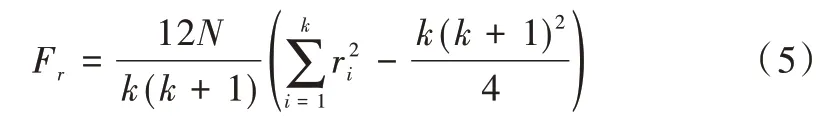
（5）由于原始的Friedman 要求k较大，过于保守，因此通常使用以下公式计算检验统计量。

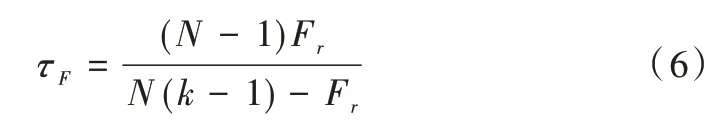
（6）如果原假设H0被拒绝，则需要进行后续检验进一步区分各算法性能。本文利用Nemenyi 进行后续检验，其临界值域的计算公式如式（7），其中qα查表可得。

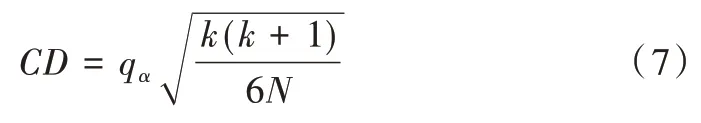
2.2 数据集描述

为了验证本文算法的适用性，按照不平衡度从小到大，选取15 个数据集，分别来源于KEEL 和UCI，数据集的详细信息如表2 所示，其中不平衡度由多数类个数除以少数类个数得到。

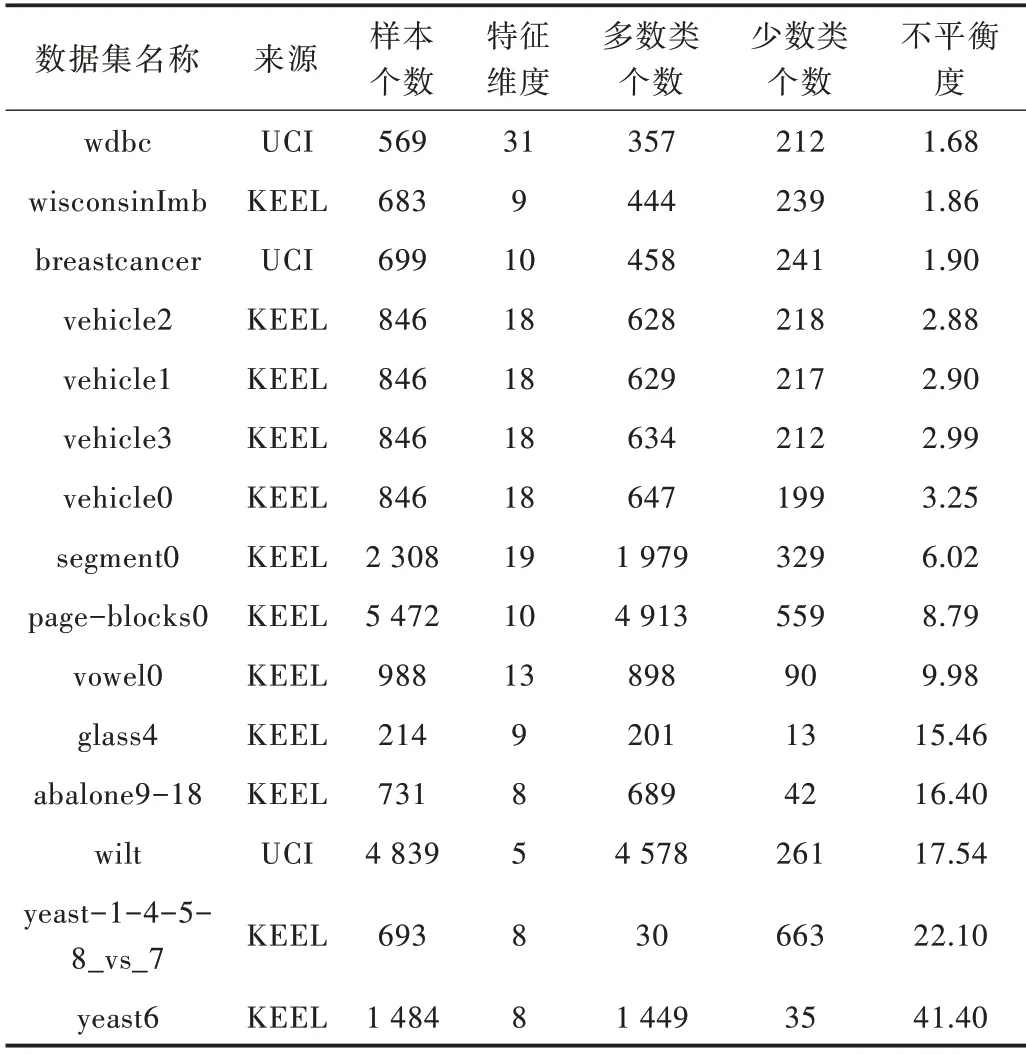
Table 2 Data set description表2 数据集描述

2.3 参数设置

为了验证本文所提出方法的有效性，选取Adaboost、AdaCost、EUSboost 和Xgboost 进行对比实验，采取5 折交叉验证取平均值作为算法表现性能的度量；选择BP 神经网络、SVM 和Xgboost 作为本文算法的基分类器。鉴于Boost⁃ing 的算法在迭代次数为10 时表现较好［23］，本文将Ada⁃boost 和EUSboost 的迭代次数设为10。具体算法参数设置如下：

（1）Adaboost：迭代次数为10 次，CART 作为弱分类器。

（2）AdaCost：多数类代价设为0.25，少数类代价设为1.00。

（3）EUSboost：迭代次数为10 次，其他参数为默认参数。

（4）XGBoost：弱分类器为gbtree，叶子节点划分时所需损失函数减少的最小值为0.1，正则化权重为2，收缩步长为0.1，迭代次数400，其他参数为默认值。

2.4 结果分析

本文利用AUC、G-mean 和F-measure 3 个指标作为评价指标，分别比较在使用本文方法前后的性能。为了更简洁地展示实验结果，将Adaboost 简写为Ada，Adacost 简写为Adac，EUSboost 简写为EUS，XGBoost 简写为Xgb。将本文方法改进后的算法后加上符号+，如Ada+表示使用本文方法改进后的Adaboost 算法，其中加粗表示效果最好。

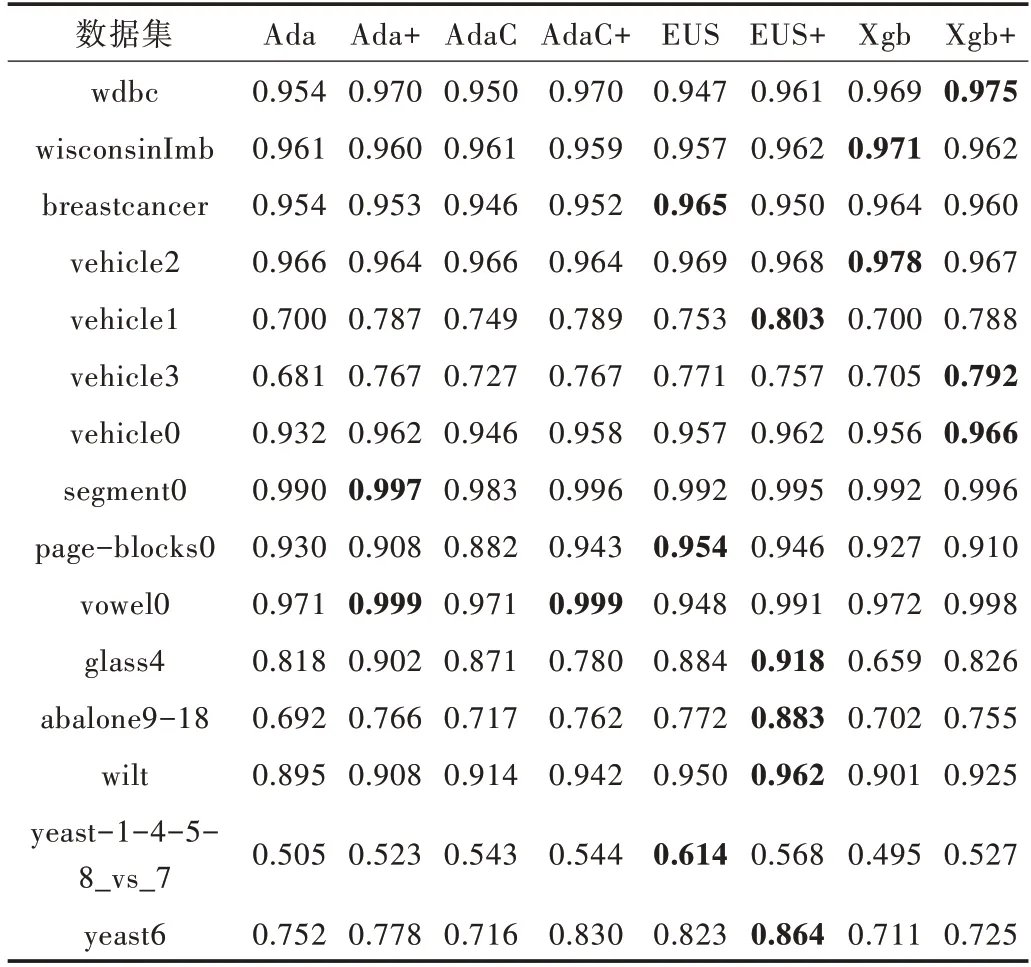
Table 3 Comparison of AUC values of various algorithms表3 各算法的AUC 值比较

通过表3 可以看出，Adaboost、AdaCost、EUSboost 和Xg⁃boost 在使用本文所提出的方法后，其AUC 值在大部分数据集上有了一定提升。在vowel0 上，改进后各算法的AUC 值均接近于1；在glass4 上，Xgboost 的AUC 值上升得最快，为16.7%。

为了更好地评价算法性能，使用Friedman 检验对表3各算法的AUC 值进行排序得到表4。

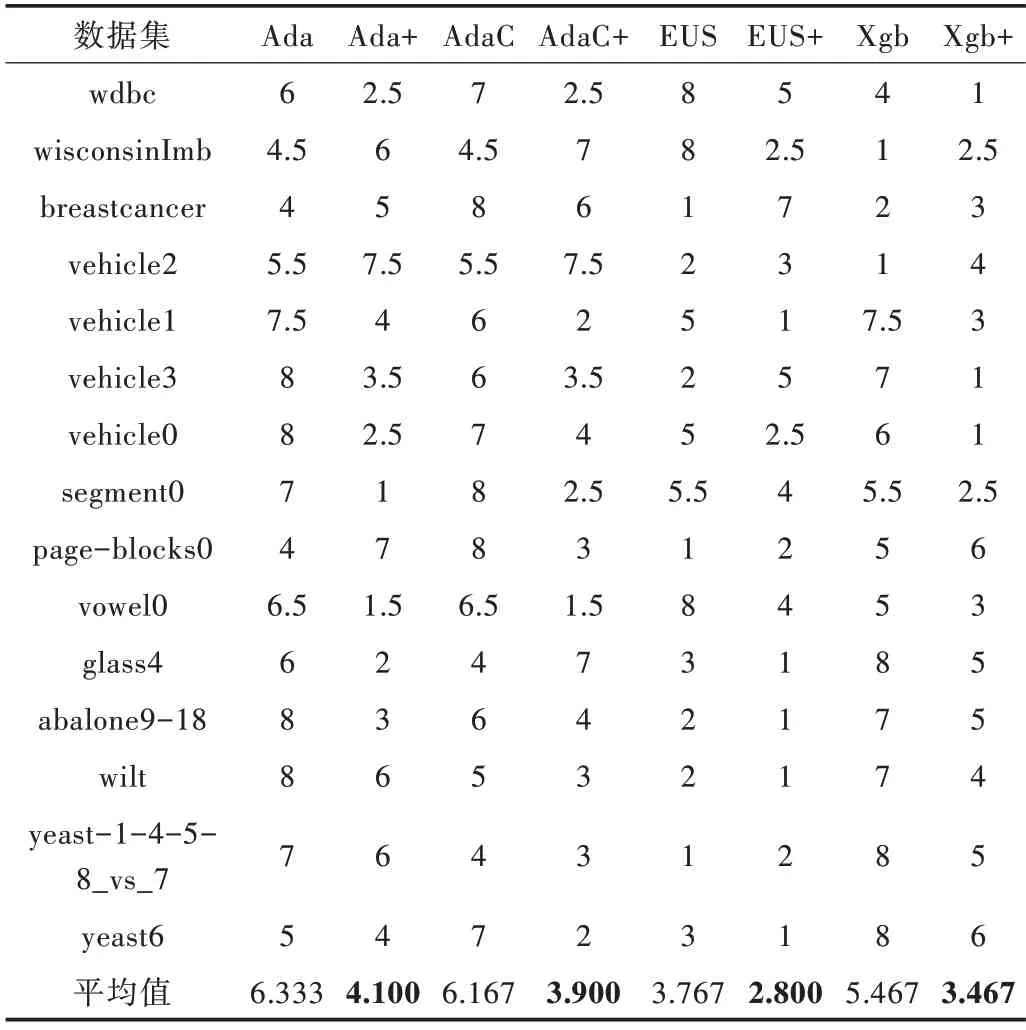
Table 4 Aligned-ranks of algorithms under AUC表4 AUC 下算法的序值

序值越小意味着算法性能越好，从表4 中可以看出，使用本文方法进行改进后，各算法平均序值都小于原始算法。

取显著性水α 平为0.05，由表4、式（5）和式（6）可得检验统计量τF=5.628，查表可知F 检验的临界值为2.104，小于τF，因此各算法性能相同这一假设被拒绝，则意味着各算法性能不相同，因此用Nemenyi 检验作进一步区分。由式（7）可计算得临界值域CD 为2.711，由临界值域和表4 可得到检验结果，用图2 表示。

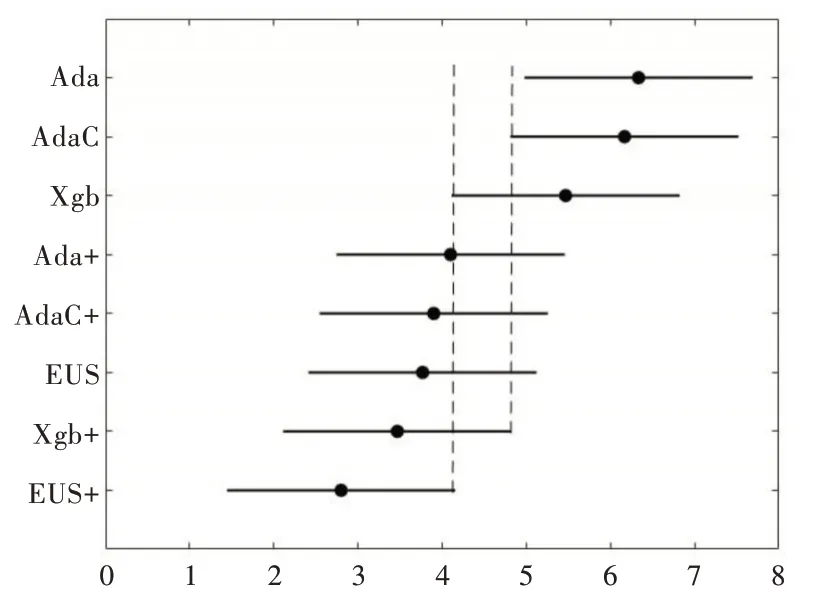
Fig.2 Friedman test chart under AUC图2 AUC 下Friedman 检验 图

由图1 可以直观地看出，经过本文方法改进后，在AUC上EUSboost 的性能优于Xgboost，显著优于AdaCost 和Ada⁃boost；改进后的Xgboost 优于AdaCost 和Adaboost。

由表5 可以看出，经过本文方法改进后的算法在大部分数据集上G-mean 有了一定提升。在yeast6 上AdaCost 的G-mean 提高了21.9%，在vowel0 上各改进后算法的Gmean 均接近于1，Xgboost 在yeast-1-4-5-8_vs_7 上 由0 提升至16.2%。

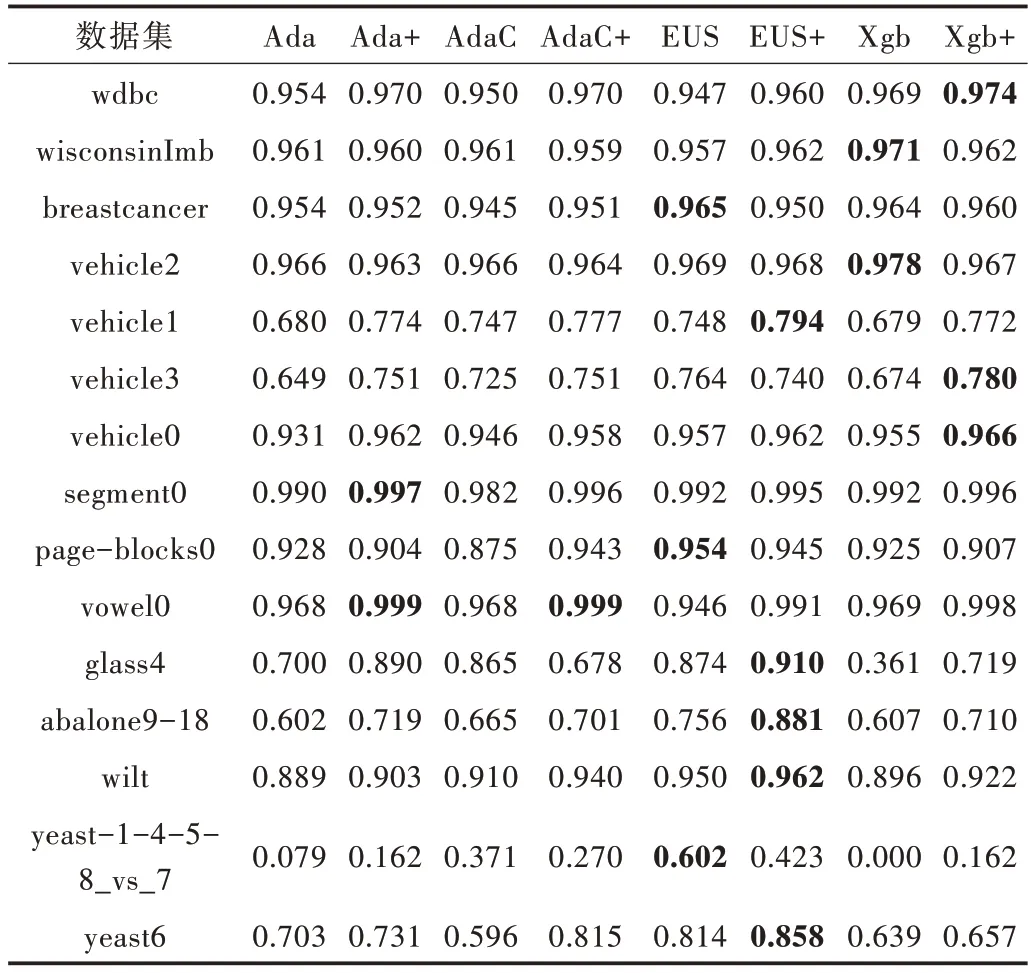
Table 5 Comparison of G-mean values of various algorithms表5 各算法的G-mean 值比较

同上，利用Friedman 检验对表5 中算法的G-mean 进行排序可以得到表6。从表6 可以看出，改进后算法的平均序值均小于原始算法。同理可以计算得检验统计量τF=5.460，大于F 检验的临界值，因此说明各算法性能不相同，存在差异，进一步使用Nemenyi 检验，各算法检验结果用图3 表示。

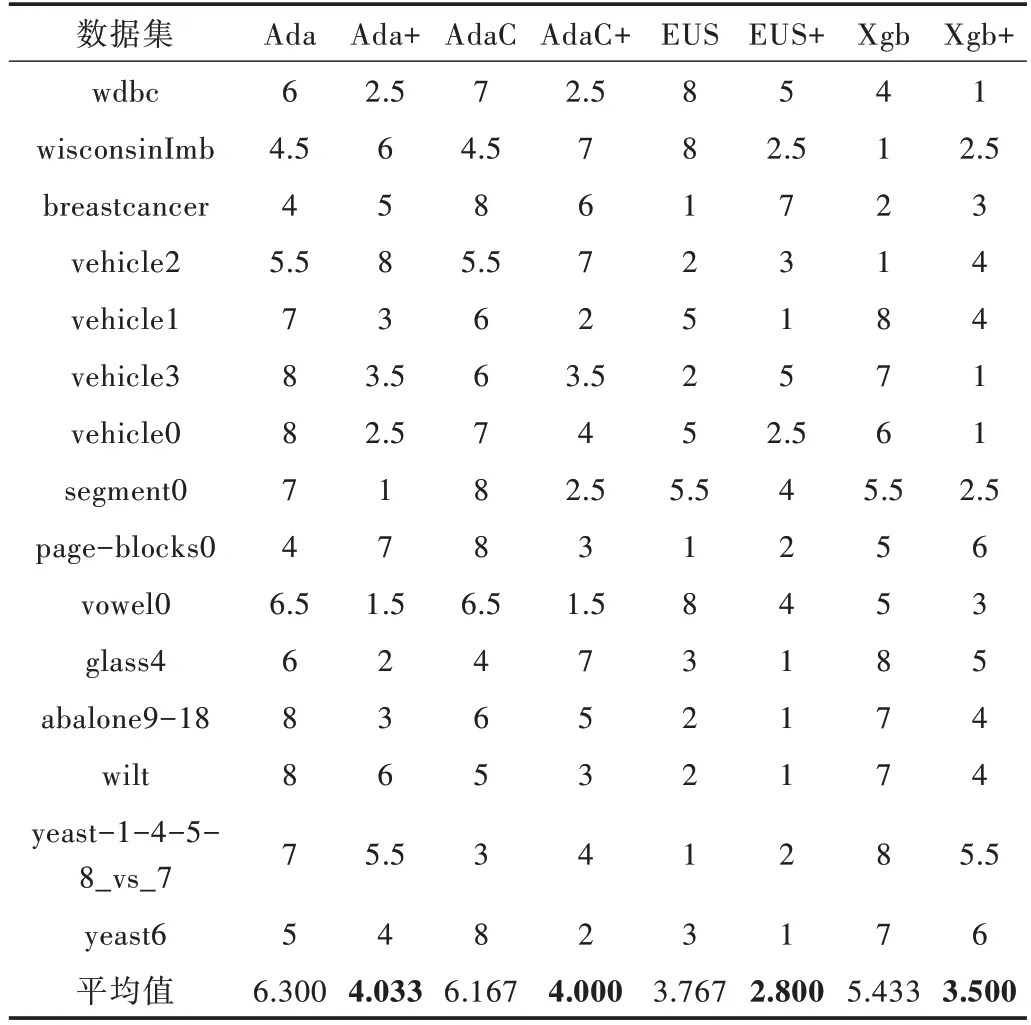
Table 6 Aligned-ranks of algorithms under G-mean表6 G-mean 下算法的序值

由图3 可以直观地看出，在G-mean 上改进后的EUS⁃boost 优于Xgboost，显著优于AdaCost 和AdaBoost；改进后的Xgboost 优于AdaCost 和AdaBoost。

在F-measure 上，由表7 可以看出，各改进后的算法在大部分数据集上均有一定提升。特别是在abalone9-18 上各算法提升较快，其中AdaCost 和EUSboost 提升效果最好，为20%左右。由表8 可知，改进后各算法平均序值均小于原始算法。

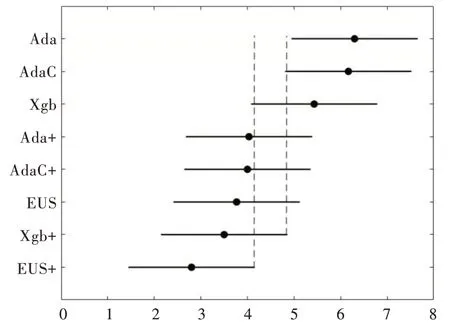
Fig.3 Friedman test chart under G-mean图3 G-mean 下Friedman 检验图

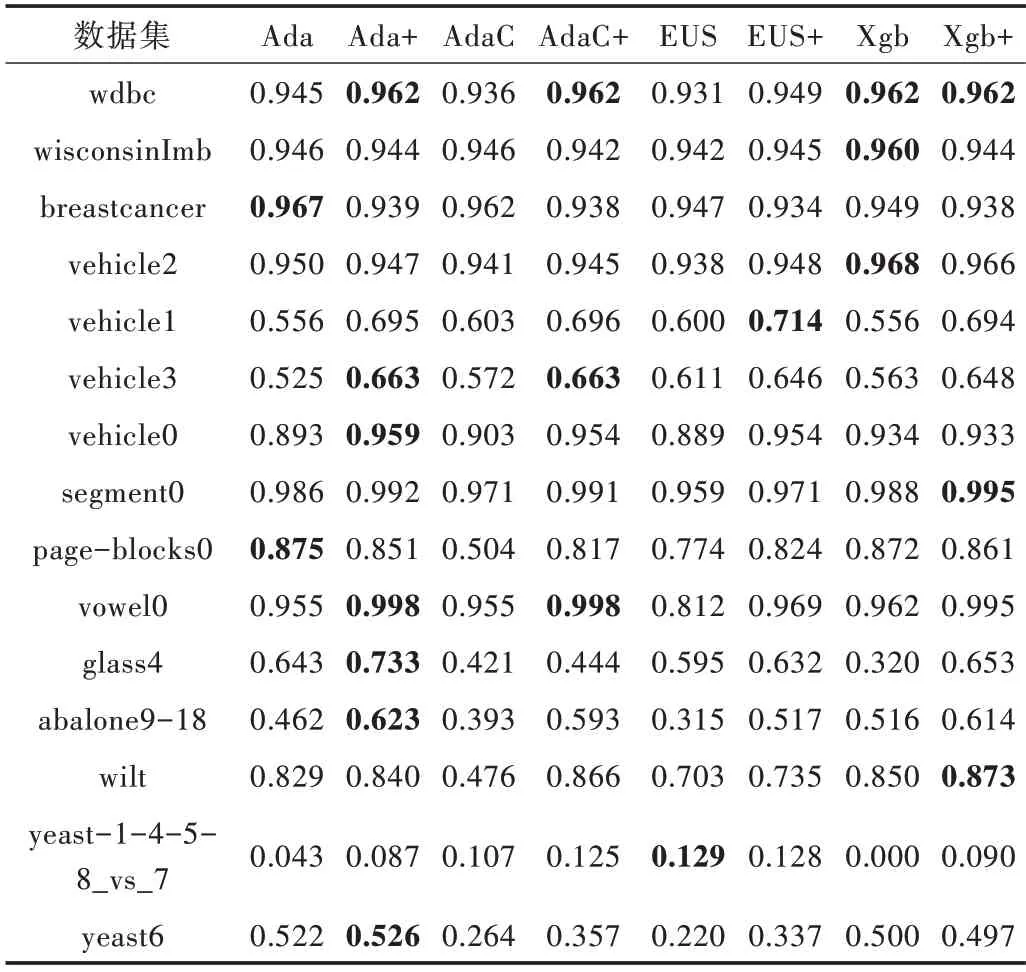
Table 7 Comparison of F-measure values of various algorithms表7 各算法的F-measure 值比较

同理计算可得检验统计量τF=4.661，大于F 检验的临界值，因此拒绝各算法性能相同这一假设，然后利用Neme⁃nyi 后续检验，其检验结果用图4 表示。

由图4 可知，在F-measure 上，改进后的Adaboos 性能显著优于AdaCost 和EUSboost；改进后的Xgboost 性能略优于AdaCost，显著优于EUSboost；改进后的AdaCost 优于EU⁃Sboost。

以上分析说明，本文所提出的方法具有一定的有效性和适用性。以vowel0 数据集为例，说明本文方法如何提高算法性能。

利用PCA 对vowel0 进行降维，取前3 个成分，累计贡献率为90.067；同样将经过本文方法改进后的vowel0 降成三维，取前3 个成分，累计贡献率为77.359。将降维后的数据绘制成散点图，其中图5 为原始数据散点图，图6 为经过本文方法改进后的数据散点图。为了更加直观地看出类与类之间的边界，将图5 的点沿着X 轴正方向和Z 轴所组成的平面进行投影，将图6 的点沿着Y 轴正方向和Z 轴所组成的平面进行投影，分别得到图7 和图8，从图8 中直观地看出类边界变得更为明显。虽然经过PCA 降成二维后，失去了部分信息，但从累计贡献率中可以看出，仍然保留了相当部分的信息，经过本文方法改进后，使得vowel0 的少数类与多数类之间的界限更加明显，从而使得改进后的算法在AUC、G-mean 和F-measure 上均接近于1。

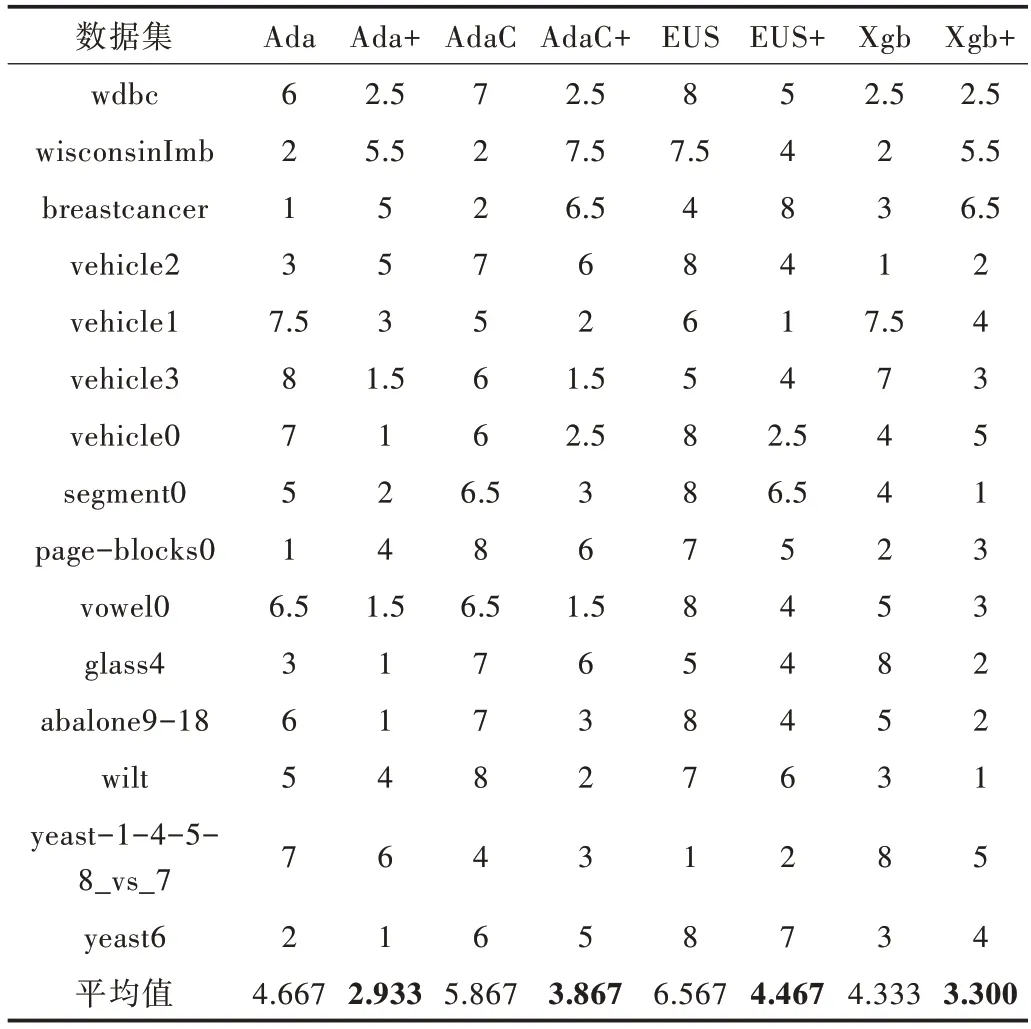
Table 8 Aligned-ranks of algorithms under F-measure表8 F-measure 下算法的序值

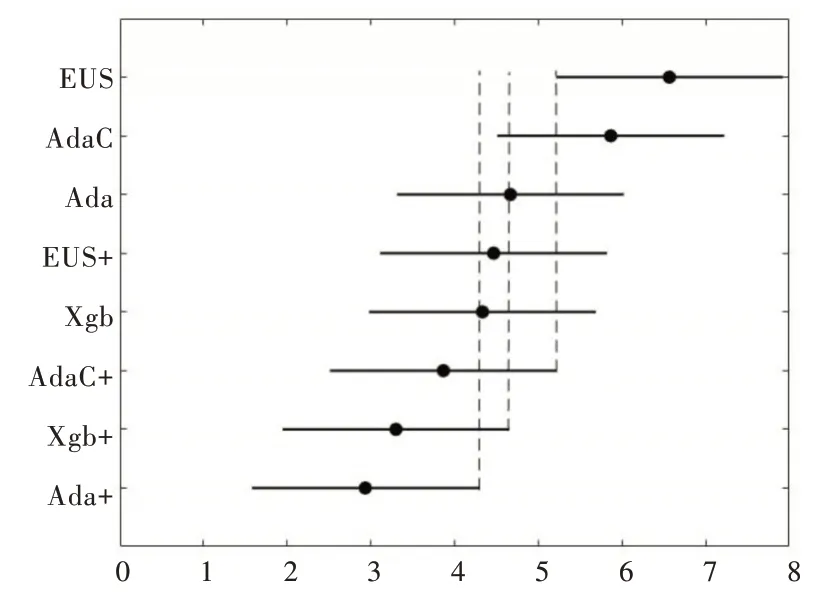
Fig.4 Friedman test chart under F-measure图4 F-measure 下Friedman 检验图

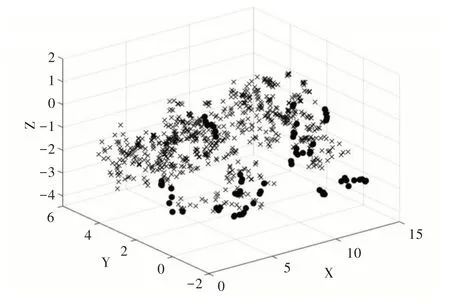
Fig.5 vowel0 three-dimensional scatter plot图5 vowel0 三维散点图

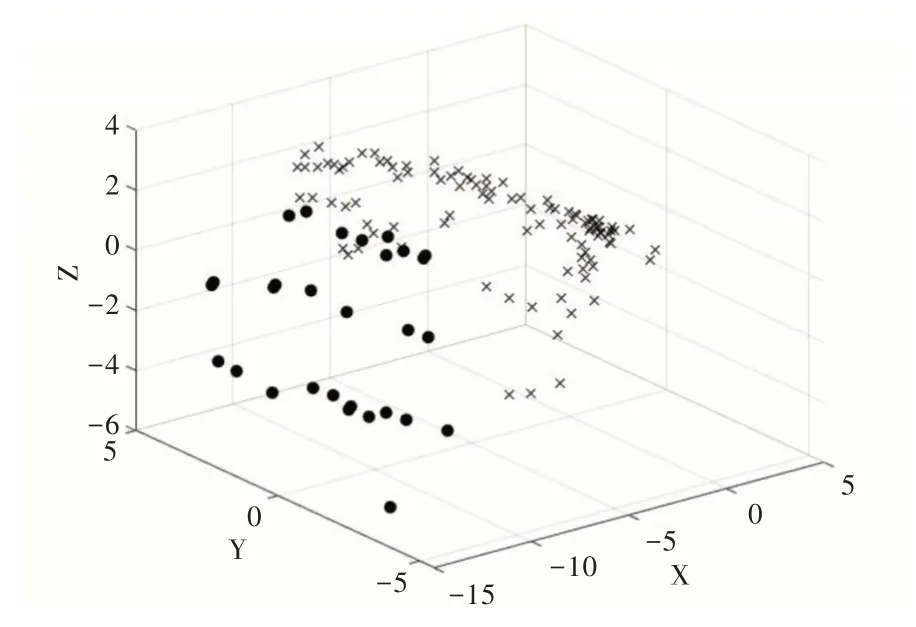
Fig.6 Improved vowel0 three-dimensional scatter plot图6 改进后的vowel0 三维维散点图

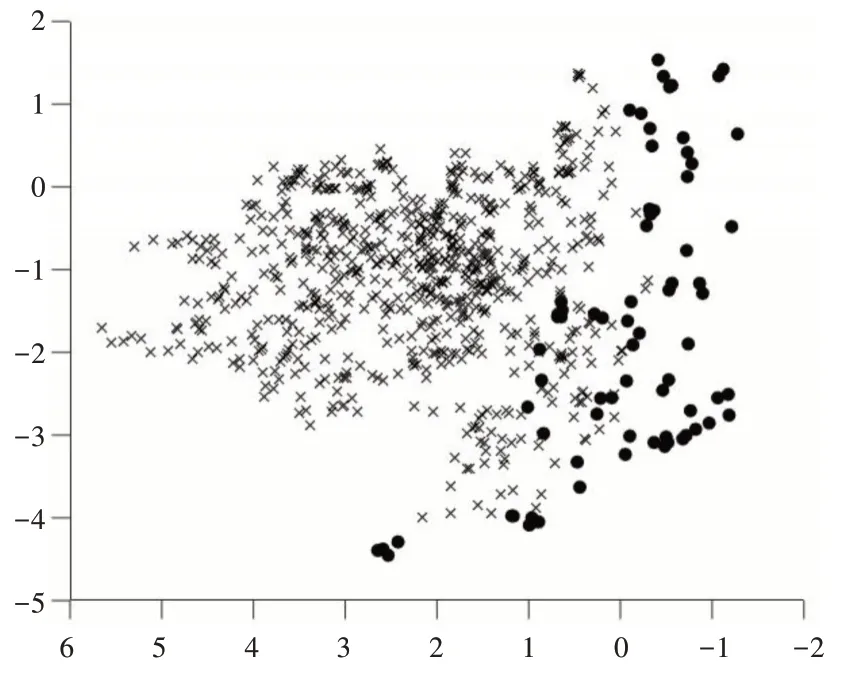
Fig.7 vowel0 two-dimensional scatter plot图7 vowel0 二维散点图

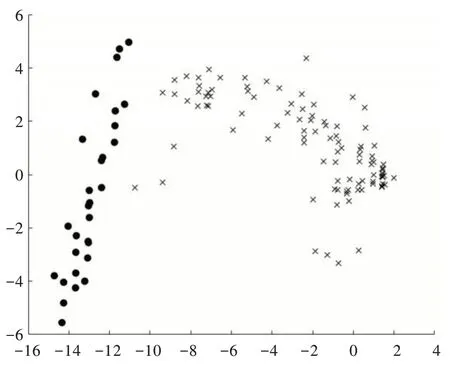
Fig.8 Improved vowel0 two-dimensional scatter plot图8 改进后的vowel0 二维散点图

3 结语

针对传统分类器不能较好地处理类不平衡问题，本文从数据和算法角度提出了融合集成思想的改进方法。该方法首先从数据层面出发，利用现有的数据集和K-means SMOTE 过采样方法构造多个类平衡的数据集；其次，从算法层面出发，集成了多个基分类器。通过对比实验分析，说明了本文方法的有效性和可行性，并且从类边界的角度分析了本文方法能够提高算法性能的原因。但是，当特征维度很高或者类极度不平衡时，训练模型的时间开销较大。同时，本文仅针对二分类问题展开了研究，存在局限性。降低时间复杂度和推广到多分类问题是后续重点研究的问题。