基于OGD 算法的在线移动平均反转策略

吴金明

（上海工程技术大学数理与统计学院，上海 201620）

0 引言

在线投资组合选择源于Kelly［1］资本增长投资理论，旨在根据资产的历史价格和策略收益的历史表现进行迭代式投资，具有不需要对金融市场分布进行假设和迭代投资的特点，相对于传统的基于Markowitz［2］均值方差理论的投资组合选择方法而言更加灵活实用，与实际投资活动更加贴近。虽然在线投资组合选择的研究成果众多，但是与实际的投资需求相比仍然存在不足，而金融市场的非平稳性问题就是其中之一［3-4］。因为金融市场是动态的、非平稳的，所以现有的静态预测模型往往不能很好地挖掘市场信息，限制了策略收益的提高。

针对此问题，本文在移动平均反转策略基础上加入在线算法，提出了在线梯度下降移动平均反转（Online Gradi⁃ent Descent Moving Average Reversion，OGDMAR）策 略。OGDMAR 策略每次迭代都会根据预测模型的损失值动态调整模型系数，从而在一定程度上克服非平稳性问题，然后再将其与包含原策略在内的6 个已有策略进行数值实验和对比分析，进一步论证本文策略的有效性。

1 研究背景

在线投资组合选择是一个交叉研究领域，该问题既可以归于金融计算领域，又可以归到机器学习或人工智能算法［5-8］。从策略角度出发分为5 大类：基准策略、追随赢家类策略、追随输家类策略、模式匹配类策略以及元学习类策略［9］。其中，基准类策略通常作为对比标准用来衡量其他策略的实际表现。虽然基准类策略的累积收益不理想，但仍具有一定的参照性，尤其是在对交易成本分析方面。而追随输家类策略实际上是对金融市场均值反转现象的探索，在累积收益方面已取得不错的成绩，但仍存在进步空间。

1.1 基准类策略

最普遍的基准策略是购买持有（Buy-And-Hold，BAH）策略。起初投资者按某一比例将资金分配到各资产中，然后不对投资权重做任何调整，一直持有到期末。该策略产生的交易成本最小，但无法获得市场短期波动带来的收益。当使用平均权重时，该策略通常称为Market 策略，用来衡量金融市场的总体收益情况。另一个比较流行的策略是最优股票策略（Best Stock，Best），投资者在事后获取所有股票信息情况下，将所有的资金投入到表现最好的股票中去。还有一个常用的基准策略——定常再调整（Con⁃stant Rebalanced Portfolio，CRP）策略。由于资产的价格变动会导致实际权重发生变化，因此在该策略中投资者事前设定一个权重的分配方案，每一期都对权重进行调整，以保持固定权重。当初始权重被设为最优的投资组合时，策略被称为最优定常再调整（Best Constant Rebalanced Portfo⁃lio，BCRP）策略［9］。

1.2 追随输家类策略

Borodin 等［10］提出反相关（Anti Correlation，Anticor）策略，通过计算正的滞后交叉相关和负的自相关的一致性来捕获均值反转规律，并将其用于预测股票价格。Li 等［11］提出被动主动均值反转（Passive Aggressive Mean Reversion，PAMR）策略，其将PA 算法创造性地引入到在线投资组合选择领域，减少上一期累积收益高于阈值资产的权重，增加上一期累积收益低于阈值的权重，从而捕捉市场中的均值反转现象。但此策略对于DJIA 这类不存在单期均值反转现象的数据集显得乏力。Li 等［12］提出置信加权均值反转（Confidence Weighted Mean Reversion，CWMR）策略，假设每期的投资组合向量服从某一多元高斯分布，使用置信权重算法结合投资组合权重协方差矩阵来探索均值反转规律。Li 等［13］提出在线移动平均反转（OnLine Moving Av⁃erage Reversion，OLMAR）策略，使用简单移动平均和指数平滑两种方法预测价格，实际上是针对PAMR 策略的多周期改进，是一种多周期的均值反转策略。Huang 等［14］提出鲁棒性中位数反转（Robust Median Reversion，RMR）策略，提出通过鲁棒的L1中位数估计器处理噪声和异常值的思路，该策略表现出较好的鲁棒性，解决了数据中包含异常值的问题。郁顺昌等［15］提出在线自回归移动平均反转（OnLine Autoregressive moving average Reversion，OLAR）策略，构建ARIMA 模型预测价格并使用在线算法求解，为处理异常值和非平稳性问题给出了新的解决方式。

1.3 问题与解决办法

在追随输家类中，多数策略都需要先对价格进行预测，然后再进行投资组合选择。而现有的预测模型大多属于静态模型，体现在模型无法随着市场变化而改变，因此无法很好地适应非平稳的金融市场。针对此问题，本文在已有的OLMAR 策略基础上引入OGD（Online Gradient De⁃scent）算法对其进行改进，从而解决该问题并进一步提高策略收益。

2 基于改进OGD 算法的OLMAR 策略

2.1 基本定义

2.2 基于OLMAR 策略的预测模型

OLMAR 策略每一期都会使用简单移动平均模型来预测下一期股票价格，然后使用PA 算法选择投资组合。由于经典数据集中的数据均为股票的比值价格，故OLMAR 策略中针对比值数据的预测模型表示如下：

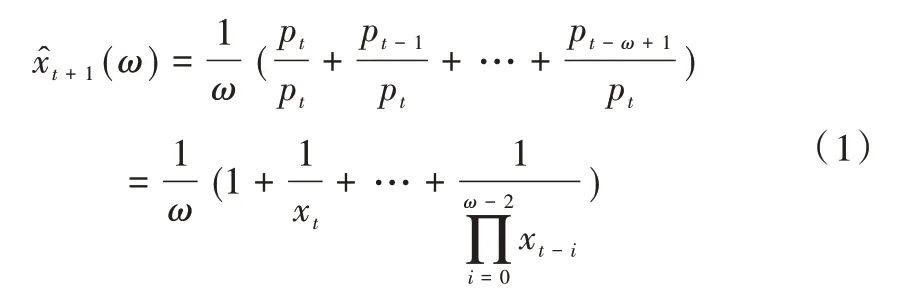
式（1）中，ω表示移动窗口大小，一般设为5，过大或过小都会影响到预测的准确性。根据观察可知式（1）中的系数固定且相等，均为，这意味着不同交易期的历史价格在预测中具有相同的重要性，而实际上不同交易期历史价格的重要程度往往是不同的，甚至会不断变化。因此，本文使用经典的OGD 算法对式（1）中的系数每一期都进行更新，旨在不断寻找不同阶段的最优预测价格。

2.3 OGD 算法在预测模型中的应用

OGD 算法是一种经典的在线学习算法，具有计算复杂度低、运算时间快的特点［16-17］。OGD 算法实际上是随机梯度下降（Stochastic Gradient Descent，SGD）算法的在线版本。为便于描述，令预测模型系数为此时预测模型表示如下：

根据式（2）可得参数更新公式如下：

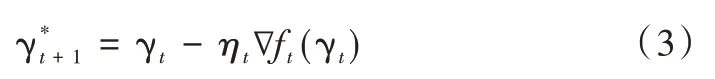
式（3）中：ηt为学习率，γt表示第t期预测模型系数，ft(γt)表示具体形式为平方误差的损失函数，∇ft(γt)表示第t期损失函数的梯度。式（3）的含义为，利用第t期损失函数中的信息寻找第t+1 期的最优参数。与SGD 算法的不同之处在于，完成更新迭代后还需要再进行一步映射，目的是避免参数超出可行域［18］。

设γ 的可行域为P ⊂Rn，公式如下：

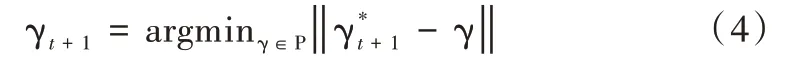
至此便得到OGDMAR 策略的预测模型，具体步骤见模型1。

2.4 OGDMAR 策略

使用OGDMAR 预测模型对下一期股票价格进行预测，再使用OLMAR 策略中的PA 算法对投资组合进行选择便可得OGDMAR 策略，具体步骤如下：

策略1 OGDMAR 在线投资组合选择策略

3 实验分析

为了说明OGDMAR 策略优势，选择6 种策略做对比，并使用4 个经典数据集。分析过程中使用累积收益和交易成本两个指标，从两个角度进行策略分析。

3.1 对比指标

3.1.1 累积收益

累积收益评估策略的盈利能力，累积收益越大意味着策略的盈利能力越强，是最重要的正向评价指标。

3.1.2 交易成本

交易成本指因资产的买卖而产生的费用，是一个负向指标，在此通过对比同样交易成本情况下不同策略累积收益的大小来分析不同策略的优劣。一般来说交易成本按照交易额的比例缴纳，因此要考虑交易费用比例。考虑交易成本之后的累积收益公式如下：

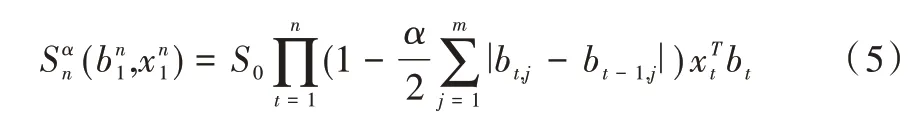
3.2 实验数据集特征

本实验使用4 个经典的公开数据集，分别为NYSE（O）、NYSE（N）、DJIA 和MSCI，具体信息如表1 所示。根据文献［4］，本文在不同的策略上使用相同的参数ε=10，ω=5。

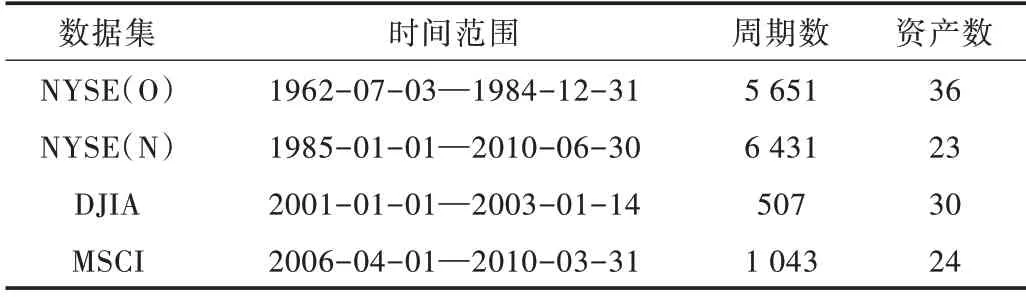
Table 1 Four classical data sets表1 4 个经典数据集

3.3 结果分析

3.3.1 累积收益

7 种策略在4 个数据集上的累积收益情况如表2 所示。与其他6 种策略相比，OGDMAR 策略表现最为突出。其在NYSE（N）、DJIA 和MSCI 三个数据集上获得了最高的累积收益。虽然在NYSE（O）数据集上的累积收益低于RMR 策略，但是高于改进前的OLMAR 策略，并且与RMR 策略的最高累积收益差别很小，只有7%。改进后的OGDMAR 策略相对于OLMAR 策略在4 个数据集上分别提高了111%、134%、32%和48%，累积收益提升显著，表明OGDMAR 策略有效。

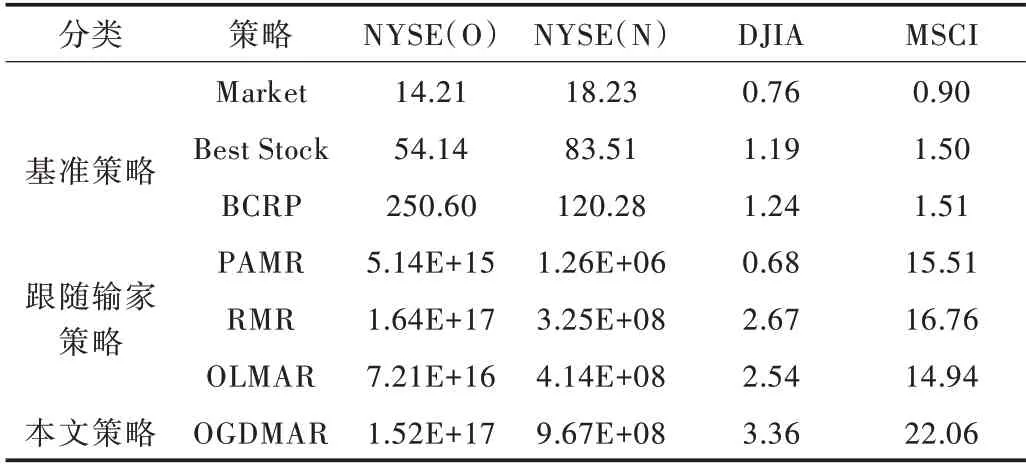
Table 2 Cumulative benefits of seven strategies on four data sets表2 7 种策略在4 个数据集上的累积收益

3.3.2 交易成本

在4 个数据集上，OGDMAR 策略与3 个对比策略随着交易成本率的增加，累积收益的变化情况如图1-图4 所示。图1 中，在NYSE（O）数据集上，OGDMAR 策略的累积收益一直高于OLMAR 策略，而且这一差距随着交易成本率的增加不断扩大，可见该数据集下交易成本率越高OGDMAR策略的优势就越明显；图2 中，OGDMAR 策略同样是随着交易成本率的增加不断拉大与OLMAR 策略的差距，但是当交易成本率高于0.5%之后，OGDMAR 策略的收益开始低于基准策略并呈现下降的趋势；图3 与图4 的情况相似。当交易成本率高于0.4%或0.5%之后，OGDMAR 策略的累积收益开始低于基准策略并呈递减式下降趋势。这说明现有的反转类策略在高交易成本率的情况下存在天生劣势，甚至差于基准策略，这可能是由其投资组合的更新规则造成的。但是，OGDMAR 策略在任何交易成本情况下都可获得比OLMAR 策略更高的累积收益，这说明改进后的OGDMAR 策略有着更强的交易成本承受能力，也再一次验证了OGDMAR 策略的有效性。

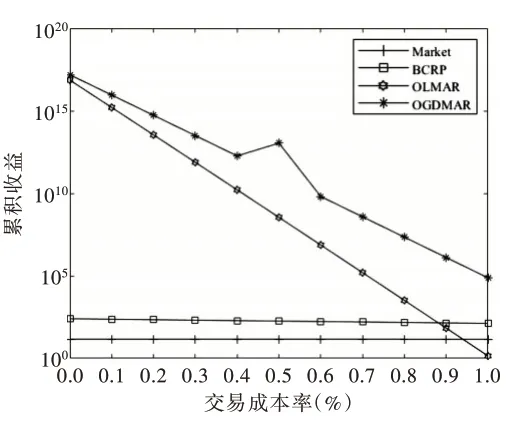
Fig.1 Transaction cost analysis of OGDMAR strategy on NYSE（O）data set图1 OGDMAR 策略在NYSE（O）数据集上的交易成本分析

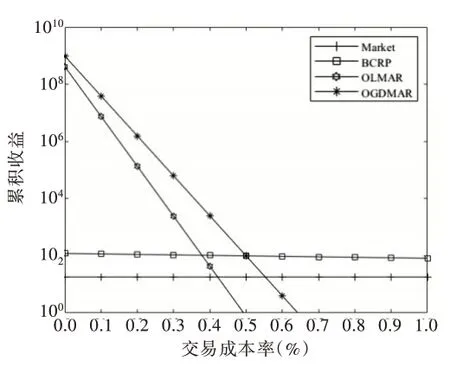
Fig.2 Transaction cost analysis of OGDMAR strategy on NYSE（N）data set图2 OGDMAR 策略在NYSE（N）数据集上的交易成本分析

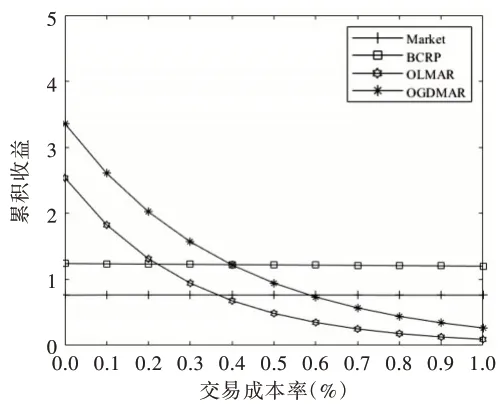
Fig.3 Transaction cost analysis of OGDMAR strategy on DJIA data set图3 OGDMAR 策略 在DJIA 数据集上的交易成本分析

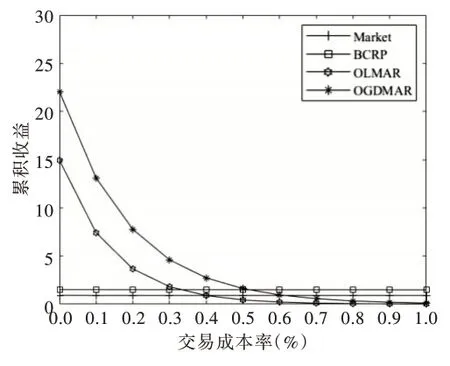
Fig.4 Transaction cost analysis of OGDMAR strategy on MSCI data set图4 OGDMAR 策 略在MSCI 数据集上的交易成本分析

4 结语

本文针对金融市场的非平稳性问题，在OLMAR 策略的基础上引入OGD 参数更新方法，提出了具有动态调整预测模型系数的OGDMAR 策略。与原策略相比，改进后的OGDMAR 策略在累积收益上获得了全面提升，同时在交易成本方面比原策略表现出更高的承受能力。但是当交易成本率较高时出现了累积收益率趋近于0 的情况。对此，后期会考虑改进投资组合的更新规则，减少不必要的交易，解决高交易成本率下累积收益过低的问题［19-20］。