一种基于PSO-DBN 的地铁转向架故障诊断方法
2021-09-28闻一波雷菊阳
闻一波,雷菊阳
(上海工程技术大学机械与汽车工程学院,上海 201620)
0 引言
随着国内各大城市地铁的不断投入使用,列车行驶过程中的安全性和舒适性越来越受到人们的重视,转向架作为列车关键部件成为列车故障研究的重点问题[1]。文献[2]提出了一种聚合经验模态分解的列车转向架故障诊断方法,研究了转向架空气弹簧失气、抗蛇形减振器失效、横向减振器失效等几种常见的列车转向架故障类型;文献[3]结合了信息测度理论与时频分析方法的分析框架,着重研究了列车转向架故障信号特征提取、关键部件性能蜕化估计、多特征融合等问题。
在对转向架状态进行分析时,通常需要在列车上安装一定数量的传感器,进而获取列车在行驶过程中的各种信息以便进行下一步的故障诊断、预测等操作[4]。目前,国内在列车运行状态基于实时监测数据的特征分析技术、列车安全性能分析与评估预警[5-6]等领域获得了大量研究成果。然而随着地铁交通的发展,现有的监测技术及特征分析、安全性能分析及预警维护等研究远不能满足地铁交通发展需求。
近年来,深度学习技术在故障诊断领域的应用逐渐深入[7]。文献[8]以转向架关键部件为研究对象,针对故障信号依据深度学习的降噪自动编解码过程进行故障特征学习,实现转向架故障信号识别;文献[9]为解决同步发电机传统故障诊断方法依赖专家经验和信号处理技术提取故障特征的问题,基于深度置信网络简历诊断模型提高诊断精度;文献[10]提出基于粒子群算法优化的BP 神经网络(PSO-BP)的故障率预测模型,对城轨列车转向架轮对轴箱进行故障率预测。
受此启发,探索将其他深度学习方法应用于地铁转向架故障诊断,深度置信网络(Deep Belief Networks,DBN)[11]作为深度学习领域的开创模型,在文字检测、人脸及语音识别[12-15]等方面得到广泛应用,粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体的智能优化算法[16],该算法具有群体智能、内在并行性、结构简单等优点。因此,本文提出一种基于粒子群优化深度置信网络即(PSODBN)模型,并将该模型应用于地铁转向架故障诊断。
1 地铁转向架故障分析及建模
利用深度学习技术解决实际问题时,需要准备一份相对完善的数据集。本文使用深度学习实现转向架关键部位故障分类,因此首先需要对转向架关键部位进行故障分析。由于发生故障在地铁实际运行过程中属于小概率事件,故障数据相较于正常状态数据为小样本,本文采用仿真方法对地铁建模,模拟大量实验数据,满足深度学习模型训练需求。
1.1 地铁转向架故障分析
转向架作为轨道车辆最重要的部件之一,它实现轨道车辆行驶功能,其结构设计是否合理关系到轨道车辆运行品质、动力性能和行车安全。120km/h 速度级B 型地铁转向架结构如图1 所示。
转向架是支撑车体及其载荷并引导车辆沿轨道运行的行驶装置,它承受着包括车体、动力装置和辅助装置等各种载荷,并保证充分的轮轨接触,同时还缓和路线不平顺对车辆的冲击,保证车辆运行过程中的平稳性和安全性。地铁转向架的关键部件主要有以下几个部分:
(1)一系悬挂弹簧与二系悬挂空气弹簧。采用弹簧减震装置可增加静挠度,减小车辆悬挂装置的总刚度,提高车辆垂向运动稳定性,减少路面对车辆的振动和冲击,目前地铁、轻轨车辆的铁路客车都采用二系悬挂装置。在车辆行驶过程中,由于气候条件、线路状况以及空气弹簧系统部件和空气弹簧本身质量等综合因素影响,空气弹簧可能出现漏风现象[17],此外空气弹簧胶囊与上盖和下座会产生滑动摩擦,使胶囊表面磨损,以及节流阀生锈和脱落也会导致空气弹簧失效。
(2)二系横向减振器。减振器[18]的主要作用是减小列车在行驶过程中的振动,消耗振动能量,提高列车运行的稳定性和安全性,目前地铁大多采用油压减振器。文献[19]中以轨道耦合动力学理论为依托,系统分析机车横向减震器的阻尼参数、工作状态、卸荷速度和悬挂位置等参数对机车平稳性的影响,得出选取适当横向减震器的结构阻尼参数,对提高机车的平稳性有利,横向减振器是否正常工作对于机车的运行品质有着较大影响,必须严格保证所有横向减振器的正常工作。
(3)轴承轴箱装置。轴承轴箱装置是轮对与构架互相连接的关键组成部件,地铁的轴箱装置主要由轴箱和轮对轴承组成,目前地铁普遍采用的是滚动轴承轴箱装置。由于轴承在运行过程中需要承受巨大的动静载荷,因而轴承的强度高、负荷能力强、耐冲击,地铁滚动轴承一般使用圆柱滚动轴承或圆锥滚动轴承。列车轴箱轴承故障[20]类型主要有以下几种类型:疲劳脱落、烧伤和磨损以及塑性变形。
1.2 地铁转向架建模
实验中使用多体动力学软件SIMPACK,对某B 型地铁车辆系统整车进行仿真得到非线性模型如图2 所示。
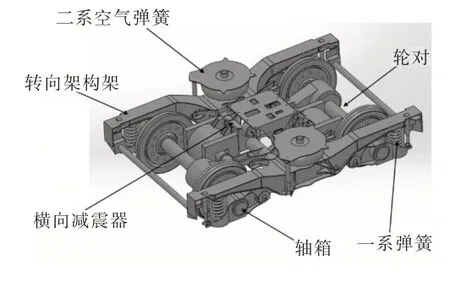
Fig.1 120km/h speed class B type subway bogie structure图1 120km/h 速度级B 型地铁转向架结构
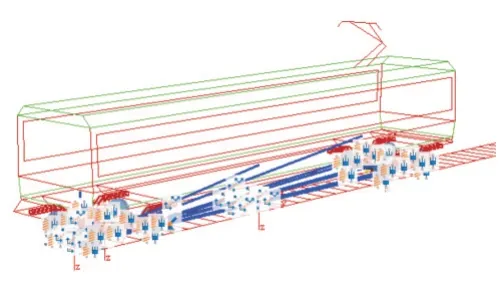
Fig.2 Simulation of B-type subway model based on SIMPACK图2 基于SIMPACK 仿真B 型地铁模型
该模型充分考虑了非线性轮轨接触几何关系、非线性轮轨相互作用力以及非线性悬挂力,实验一共准备了9 种故障类型,其中5 种单一故障,4 种混合故障。
(1)单一故障。车辆正常状态、一系悬挂弹簧故障、二系悬挂空气弹簧故障、二系横向减振器故障、轴箱轴承故障。
(2)混合故障。二系悬挂空气弹簧故障与二系横向减振器故障;二系悬挂空气弹簧故障与轴箱轴承故障;一系悬挂弹簧故障与二系横向减振器故障;轴箱轴承故障与二系横向减振器故障。
仿真实验记录了列车车体以及转向架相关部位的振动信号,主要包括车体、构架、轴箱上各部位横向、纵向和垂向加速度和位移,共得到35 个通道数据,每个通道代表列车或转向架上不同的采样位置。
2 PSO-DBN 模型
2.1 模型优化目标
在使用DBN 解决实际问题时不可避免地需要设计DBN 网络结构,但是目前很少有关于DBN 网络结构设计方面的研究,也没有制定标准规则[21]。文献[22]提出DBNNN 路径初始化DBN 隐藏层神经元数目,将该方法应用于标准数据测试,得到了更好的分类效果;文献[23]提出通过遗传算法优化设计RBM 网络结构的方法,该方法降低了可见层特征维数,提升了模型整体性能。
DBN 网络结构如图3 所示,其从本质上是由多个受限玻尔兹曼机[24](RBM)堆叠而成,采用对比散度算法和逐层预训练方法完成网络连接权值的学习。因此,使用DBN 解决实际问题时重点在于DBN 网络结构设计,当数据集确定时,输入层特征维数、各隐藏层神经元数目以及隐藏层层数共同决定了模型复杂度。输入层特征维数过多,可能会造成特征冗余的局面,增加模型复杂度,如果输入层特征维数过少,又无法保证隐藏层得到充分的数据信息。隐藏层是对输入层数据的学习,设置过多的神经元数目,迭代计算复杂,过少又无法学习到输入数据之间的差异,导致模型最终分类效果很差。而对于隐藏层层数,本文采用确定层数设计,层数设为3。
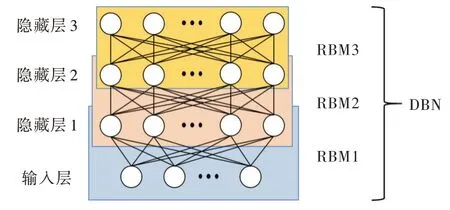
Fig.3 DBN network structure diagram图3 DBN 网络结构示意图
因此,PSO-DBN 主要优化DBN 网络结构设计,具体体现在两个方面:①粒子群算法通过粒子编码设计为DBN 输入层筛选特征维数;②粒子群算法对各隐藏层神经元数目进行优化设置。
2.2 模型算法设计
将粒子群算法应用于DBN 网络结构的优化设计,根据基本粒子群算法模型进行算法设计需要解决两个问题:个体变量设计和适应度函数设计。
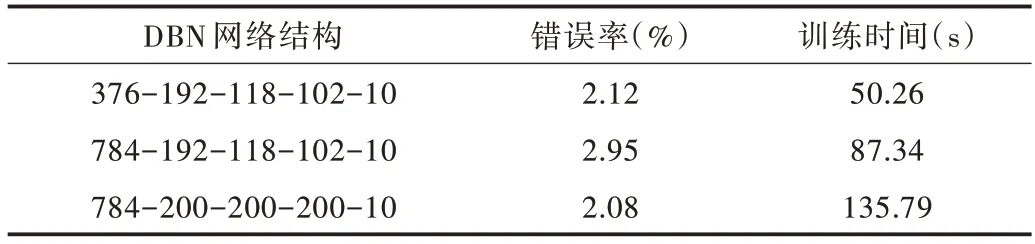
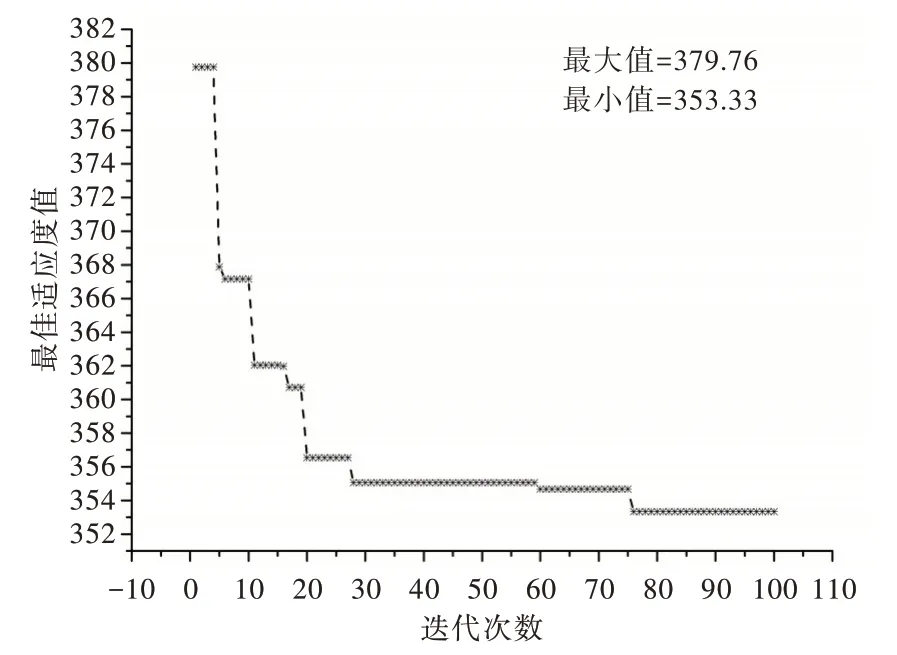
(1)个体变量设计。个体由两部分组成,分别为可见层特征维数和各隐藏层神经元数目,粒子群算法中粒子编码通常采用连续性变量。因此,个体变量设计方法如下:假设可见层特征维数为N,生成N 维的随机向量Xi=[xi1,xi2,…,xik,…,xiN](k 式(1)中,yik的取值1、0,分别表示对第k维特征的选用和舍弃。隐藏层层数及数目设计上,由于隐藏层层数选择决定层数设计且为3 层,于是隐藏层神经元数目只需要随机生成一个实数迭代训练且在DBN 中取整即可。 综上,一个个体可以表示为pop(i)=[xi1,xi2,…,xik,…,xiN,bi1,bi2,bi3]。其中,pop(i) 代表第i个个体,bi1、bi2、bi3分别表示为每一层隐藏层神经元的个数。 (2)适应度函数设计。适应度函数设计采用DBN 模型中的误差重构方法,即输入数据与重构输入数据之间的差值,采用二阶范数,公式如式(2)所示。 其中,S和N分别代表训练样本个数和可见层特征维数,M 表示DBN 中隐藏层的层数,代表在N 维特征维数的原始数据中被选中的第j维的向量。代表被选中的第j维特征数据向量经过输入重构后的向量。很显然,当适应度值E(k) 越小时,则该个体转变后的模型参数在DBN 模型使用中效果越好。 实验中使用Matlab 进行编程分析,将PSO-DBN 应用于MNIST 手写体数据集以优化DBN 网络结构,与传统的DBN网络结构在错误率和训练时间上进行比较,验证经过粒子群算法优化过的结构是否优于传统结构。MNIST 数据集包含70 000个样本,其中60 000个样本作为训练数据集,10 000个作为测试数据集。每一个样本代表一个手写数字,一共10 种数字类别,维度为28x28,展开为行向量为1x784,因此可见层特征维数N 为784。最后加上3 个隐藏层数目参数,则最终在粒子群算法中每个个体的维数等于787。 粒子群优化算法中,参数设置如下:学习因子c1=c2=1.494。个体由两部分构成,因此它们的速度和位置搜索空间都不同。可见层特征维数:速度Vmax=0.2,Vmin=-0.2,位置Fpopmax=1,Fpopmin=-1。隐藏层数目:速度Lmax=5,Lmin=-5,位置Lpopmax=250,Lpopmin=80。种群数目设为8,迭代100 次停止。经过100 次迭代寻优收敛到最优个体,将最优个体分成两部分解析,输入层特征维数由784 下降到376,各隐藏层神经元数目依次为192、118、102。 图4 展示了10 张从原始数字到降维后的数字图片,图中上部5 张为原始数据集中的数字图片,下部5 张为经过降维后的图片。可以看出,粒子群算法收敛得到的最优个体中输入层特征维数,对原始数据维数进行了筛选,虽然降维后的图片没有原来的图片清晰,但也充分保留了数字的基本特征。 Fig.4 The original number and the reduced dimension number图4 原始数字及降维后的数字 为了能够更加直观地对比出PSO-DBN 与传统DBN 结构在错误率和训练时间上的差距,实验选择了3 种DBN 结构进行比较分析,结构如下:①PSO-DBN 经过粒子群算法优化后的DBN 376-192-118-102-10;②DBN 原始数据特征维数与优化后的隐藏层神经元数目784-192-118-102-10;③DBN 原始数据特征维数与较多的神经元数目784-200-200-200-10。 Table 1 Test results of three types of DBN structures表1 3 种DBN 结构试验结果 从表1 可以看出,经过粒子群算法优化后的DBN 网络结构错误率比结构(2)低0.83%,比结构(3)略高出0.04%,但是训练时间最低,训练时间比结构(2)快37.08s,比结构(3)快85.53s。 综上可以得出,粒子群算法优化的DBN 网络结构不仅降低了输入层特征维数,剔除了输入层中冗余的特征,而且对隐藏层神经元数目进行优化设置,在错误率和训练时间上综合分析,提高了DBN 模型性能。 广泛应用于故障诊断的特征参数主要有两类:状态特征信号的特征参数和状态特征信号的数学模型参数。本文主要从时域特征参数、频域特征参数、小波包分解方法提取每一个通道的数据特征作为DBN 网络模型的输入层数据。 (1)时域特征参数。选用均值、峰值、方差、均方值、均方根值、方根幅值、偏度、峭度、波形系数、峰值系数、脉冲系数、裕度系数、偏度系数、峭度系数。 (2)频域特征参数。选用了重心频率、均方频率、频率方差。 (3)小波包分解。使用db5 小波包对原始振动信号进行3 层分解,得到8 个子频带成分的信号,使用归一化的能量矩作为元素构造出一个特征向量即作为8 个特征参数。 地铁仿真模型模拟行驶时,数据采集通道一共35 个,采样频率为200Hz,每间隔1s 采集数据作为1 个分析样本,从时域、频域和小波包分解对该样本进行分析,得到25 个参数,因此计算得出输入层特征维数为875。 实验将PSO-DBN 模型应用于转向架故障信号特征提取的数据集上,并与传统经验设计的DBN 网络结构模型在正确率和训练时间上作比较。数据集一共包含54 000 个样本,其中45 000 个样本作为训练数据,9 000 个样本作为测试数据。DBN 输入层特征维数为875,再加上3 个隐藏层神经元数目参数,最终在粒子群算法中,每个个体的维数等于878。 粒子群优化算法中,参数设置如下:学习因子c1=c2=1.494。个体由两部分构成,因此它们的速度和位置搜索空间都不同。可见层特征维数:速度Vmax=0.2,Vmin=-0.2,位置Fpopmax=1,Fpopmin=-1。隐藏层数目:速度Lmax=5,Lmin=-5,位置Lpopmax=700,Lpopmin=500。种群数目设为8,迭代100 次停止。为了提高算法求解效率,在求适应度值时DBN 模型训练次数设为1。由于粒子群算法容易陷入局部极小值[25],因此实验一共实施5 次,选取其中一次结果作为示例。 Fig.5 Best fitness convergence curve图5 最佳适应度收敛曲线 图5 表示示例迭代次数与各代中的最佳适应度值的变化关系。可以看出,随着迭代次数的增加,PSO-DBN 模型最终收敛到最优处,将最优个体转变后得到可见层特征维数由875 下降到420,同时通过粒子群算法自适应优化,对于三层隐藏层神经元数目,最终优化依次为602、618、664。对比依靠经验选择的隐藏层神经元数目即800、700、600 的选择方式,本文输出层设置9 个神经元,表示9 种故障类型发生故障的概率,将PSO-DBN 模型训练结果与经验DBN模型训练结果作对比,如表2 所示。 Table 2 Experimental results of two kinds of DBN structures表2 两种DBN 结构试验结果 从表2 可以看出,经过粒子群算法优化的DBN 模型PSO-DBN 测试正确率比经验DBN 网络模型正确率高出13.37%,而且训练时间也比经验DBN 快325.03s。综上可以得到如下结论:①DBN 模型中可见层特征维数经过粒子群算法迭代寻优,舍弃了原始数据中冗余的特征,降低了数据特征维数,从正确率和训练时间上综合分析,极大地提升了DBN 模型性能;②PSO-DBN 模型应用于解决地铁转向架故障诊断,从正确率上看,已经基本具备分类诊断分析转向架关键部位的能力。 本文采用粒子群算法优化DBN 网络结构设计,实现了可见层特征维数的冗余特征剔除以及隐藏层神经元数目的自适应选择。将PSO-DBN 模型应用于地铁转向架故障类型分类预测,实验结果表明,PSO-DBN 模型相较于经验设计的DBN 模型不仅在正确率有了大幅度提高,而且还降低了训练时间。本文通过粒子群算法优化DBN 网络结构,目的是以数据驱动思想解决地铁转向架故障诊断问题,虽然从结果来看已经基本实现了故障诊断效果,然而考虑到粒子群算法的局限性及正确率,地铁转向架故障诊断研究还有进一步提高的空间。今后工作中将继续优化PSODBN 模型,使得DBN 网络结构更加高效、便捷地应用于地铁转向架故障诊断。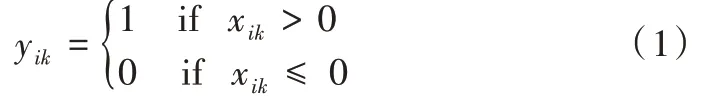
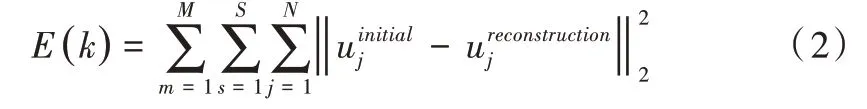
2.3 模型验证

3 PSO-DBN 转向架故障诊断分析
3.1 故障信号特征参数选取
3.2 实验分析

4 结语
