多特征融合CNN 网络的旋转机械故障诊断研究

冷 佳，刘 镇，张笑非，汤浩宇

（1.江苏科技大学 计算机学院，江苏 镇江 212100；2.江苏科技大学苏州理工学院电气与信息工程学院，江苏苏州 215600）

0 引言

轴承是最基本、最重要的机械部件之一，它的任何部位出现故障都可能导致机器运行状况恶化，发生机械故障和人员伤亡。因此，准确识别轴承故障至关重要。基于振动信号分析的故障诊断方法能有效诊断机械缺陷［1］。轴承振动信号分析是故障诊断和故障检测的重要途径。用于轴承故障诊断的振动信号处理方法一般包括特征提取和模型选择与构建两个阶段［2］。

在提取信号特征方面广泛使用的是时域分析、频域分析和时频域分析方法。典型的时域分析是从时间序列信号中计算统计条件指标，常用的条件指标包括描述性统计，如平均值、峰值、峰间间隔和标准差。采用均方根（Root Mean Square，MS）、波峰因子等简单条件指标检测局部轴承缺陷的效果有限［3］。由于频域分析可以很容易地分离和识别某些重要信号特征，它比时域分析有一定优势；快速傅里叶变换（Fast Fourier Transform，FFT）［4］是一种典型的频域分析方法，FFT 可有效获取窄带光谱。在轴承故障诊断中，高频段和低频段的频谱成分都是有价值的，特别是滚动轴承的缺陷在运行过程中产生短暂的脉冲，导致特定频段内高能。一般采用时频域分析方法来扩展非平稳波形信号的频域分析能力，常见的时频域分析方法有短时傅里叶变换（Short-Fourier Transform，STFT）［5］、Wigner-Ville 分布［6］和小波变换（WT）［7-8］等，它们可以处理非平稳信号进行机器故障诊断。然而，短时傅立叶变换无法同时达到最佳的时频分辨率，Wigner-Ville 分布的交叉项接口以及小波变换的能量泄漏问题和基函数选择的准确性［9］限制了这些方法在轴承故障诊断中的应用。希尔伯特—黄变换（Hilbert-Huang Transform，HHT）中的经验模态分解（Empirical Mode Decomposition，EMD）是一种应用于旋转机械故障诊断的强时频域分析方法，它对不含基函数的信号进行分解，适用于平稳信号和非平稳信号［10］。虽然EMD相关方法已经取得了成果，但随着工况的变化，其计算量大、结果复杂［11］。

故障诊断领域常选择机器学习作为分类工具，如隐马尔科夫模型、贝叶斯网络、反向传播（Back Propagation）神经网络、支持向量机等。由于这些算法的网络结构较浅，所以特征提取能力比较差，从而难以挖掘到故障数据更深层次的微小特征。深度学习是机器学习的一个分支，因其易于训练和分类精度高而成为实现特征提取和故障识别的有效工具；为了克服传统人工神经网络（Artificial Neural Network，ANNs）的不足，Lei 等［12］提出由堆叠自编码器（Stacked_AutoEncoder，SAEs）组成的深度神经网络（Deep Neural Networks，DNNs）对滚动轴承和行星齿轮箱进行故障诊断，但是该方法需要将原始数据转化为频谱信号；卷积神经网络（Convolutional neural network，CNN）作为深度学习的一个重要分支，由于其具有稀疏连通性、共享权值和局部域的特点，能够更好地提取深度特征，抑制网络过拟合［13］，因此可用于CNN 完成轴承故障诊断。Zhang 等［14］直接将原始时间信号作为1D CNN 输入，实现了端到端轴承故障诊断，在噪声和不同工作负载下实现了较高的诊断性能；Peng 等［15］提出基于一维CNN 的残差学习与原始振动信号相结合的变载荷轴承诊断方法，但原始振动信号并不能直观表征轴承的故障特征。针对以上使用的原始振动信号，一些研究者尝试从图像处理角度实现轴承的智能故障诊断，提供一种新的诊断思路；Li 等［16］利用STFT 和CNN 对轴承故障特征进行提取和分类；Ding 等［17］利用深度卷积网络自动学习小波包能量（Wavelet Packet Energy，WPE），生成图像的多尺度特征用于轴承故障诊断。但如果只是将一维原始的故障信号转化成二维的特征图，对故障信号直接处理会很不方便，而且很容易丢失某些故障数据的重要特征，导致分类不准确。

根据以上分析，本文提出一种多特征融合CNN 网络的旋转机械故障诊断方法。该方法首先对振动信号进行连续小波变换，得到二维小波时频图；然后构建多特征融合CNN 网络模型。其中，原始一维旋转机械振动信号作为1DCNN 模型的输入，变换而来的二维小波时频图作为2D CNN 模型的输入；然后将它们分别进行卷积层和池化层的特征提取，得到拉伸后的特征向量；最后，两组训练数据在汇聚层进行拼接，经过全连接层和分类层后实现不同旋转机械故障的具体分类。本文将一维旋转机械振动信号、二维时频图和CNN 相结合，既可以输入时域特征，又可以输入时频特征，最后利用CNN 来实现多特征融合。该方法明显的优点是既最大程度地保留了原始一维振动信号的某些重要原始特征，又充分发挥了卷积神经网络对二维图像分类精确度高的优势，从而丰富了不同维度特征，进而提高了旋转机械故障诊断的准确率。

1 连续小波变换

小波变换广泛应用于提取原始信号的时域和频域特征，通过平移获取信号时域信息，通过缩放小波母函数的尺寸获取信号频域信息。它对信号的时频域可以局部放大分析，调整尺度因子大小来改变低频信号和高频信号的时间分辨率及频率分辨率，以适应不同成分的信号，因而小波分析法在故障诊断方面效果很好。

基本小波函数ψ(t)通常称为母小波函数，在此基础上，一组时间尺度小波ψa,b(t)可用尺度和平移平差表示：

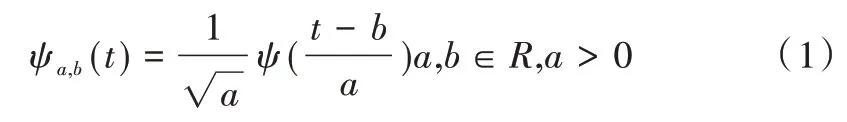
其中，a和b分别为尺度因子和平移因子。

对于任意信号函数ψ(t) ∈L2(R)，相应的连续小波变换定义为：

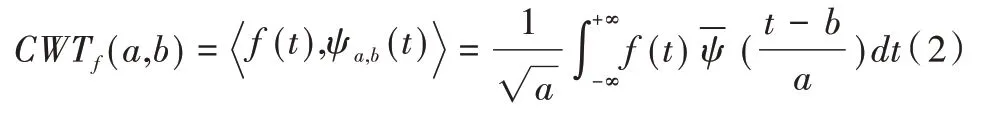
2 卷积神经网络

CNN 是一种深度神经网络，其特点是神经元的结构具有权值和偏差，可以通过训练进行调整。CNN 结构主要由一个输入层、一个输出层和多个隐藏层组成，其中隐藏层通常包含卷积层、池化层和全连接层，其基本结构如图1 所示。许多CNN 结构已经在图像处理、形状识别和视频分析中得到应用，这些都证明了CNN 模型的有效性［18-19］。

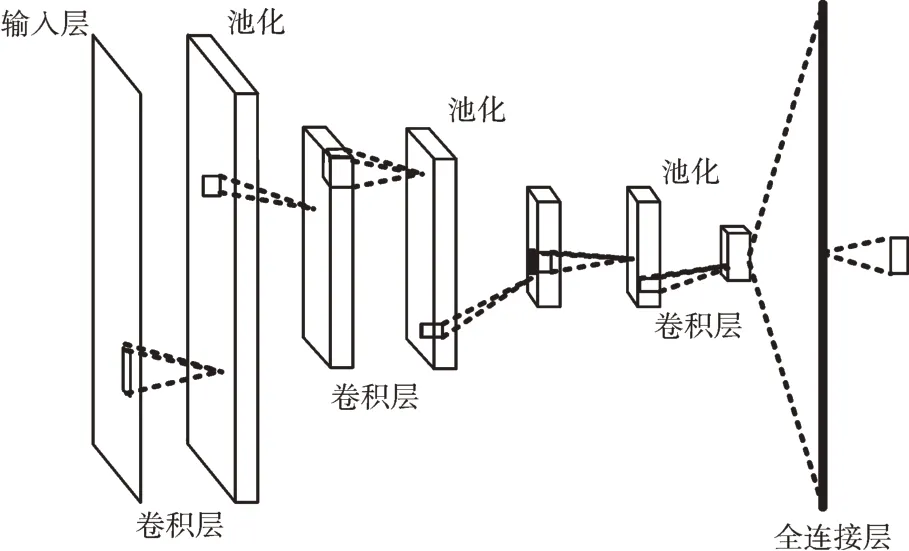
Fig.1 Basic structure of CNN network图1 CNN 网络基本结构

2.1 一维卷积神经网络

1D CNN 对于从序列数据［20］中提取重要的特征非常有效。一维信号输入网络模型后，自动逐层提取特征，且提取特征的抽象程度逐渐变高，提取的特征经过全连接层和输入层，从而实现对一维信号不同种类的分类。

2.2 二维卷积神经网络

2D CNN 对于从二维图像［21］中提取有用特征很有效，它也可以用来提取二维信号结构特征，同样适用于时频图的特征学习和识别。二维信号或图像输入网络模型后，经过卷积层、池化层和全连接层后，输出为不同信号或图像的具体分类。

2.3 卷积神经网络结构

2.3.1 输入层

卷积神经网络输入层可以处理多维数据。一维卷积神经网络的输入层接收一维或二维数组，其中一维数组通常为时间或频谱采样，二维数组可能包含多个通道。二维卷积神经网络的输入层接收二维或三维数组。卷积神经网络的输入表达式为：

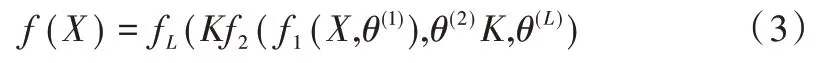
其中，X为初始输入数据，θ(1)、θ(2)、K、θ(L)为学习变量参数，即每一级对应的偏置与权重，f1、Kf2、fL为每一级相应的函数，每一级的输出结构均为特征映射矩阵。

2.3.2 卷积层

卷积层由若干卷积核卷积运算得到的特征图组成，卷积核具有局部感知和参数共享特性，在学习到多种特征表示的同时能大幅减少模型参数量。卷积层通过一组核权重和一个激活函数生成一个输出特征图。卷积运算可以表示为：

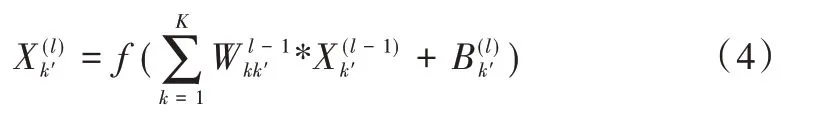
其中，l表示神经网络的层数序号，k'为输出特征映射矩阵的序号，k为输入特征映射矩阵的序号，分别为第l层中第k'个神经元的输入和偏置，为第l-1 层中第k'个神经元与第l层中第k个神经元之间的卷积核，为第l-1 层的第k'个神经元的输出，K 为第l-1 层神经元个数。

为了增加网络的非线性，在每个卷积操作之后通常还会应用激活函数。为了有效防止梯度消失和加快网络收敛速度，激活函数采用修正线性单元（rectified linear unit，ReLU），表达式为：

式（5）中，xijk为第k个特征映射矩阵的(i,j)元素。

因此卷积层中每个神经元的最终输出为：

2.3.3 池化层

在每个卷积层之后都有一个池化层。池化层是减少输入特性的水平和垂直空间的操作。池化层根据输入数据的通道数产生输出数据。在图像识别领域，主要采用最大池化，即取某位置相邻区域内的最大值作为该位置的最终输出。最大池化公式为：

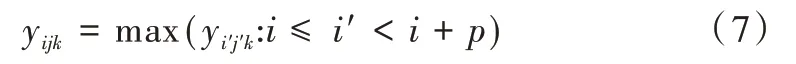
其中，p为池化窗口长度，yi'j'k为池化之前区域值，yijk为池化处理之后的值。

2.3.4 全连接层

池化层之后是完全连接层。全连通层中的每个神经元都连接到最后一个池化层中的所有特征映射，提取全连通层中的高级特征作为输出层的输入，然后生成CNN 模型的预测输出。全连接层正向传播表达式为：

3 连续小波变换和双流CNN 的故障诊断方法

本文所提出的多特征融合CNN 网络旋转机械故障诊断方法流程如下：首先对传感器获得的原始一维振动信号进行连续小波变换（Continuous Wavelet Transform，CWT），得到小波时频图；然后构建多特征融合CNN 网络模型，将一维旋转机械振动信号输入到双流CNN 的1D CNN 模型中，将得到的小波时频图输入到双流CNN 的2D CNN 模型中，分别进行卷积层和池化层的特征提取后，拉伸为特征向量；随后在汇聚层进行拼接；最后经过全连接层和分类层得到不同旋转机械故障的具体分类结果，流程如图2 所示。

3.1 获取数据集

在数据预处理阶段，利用CNN 能够实现多特征融合，即既可将时域特征作为网络输入，又可将时频特征作为网络输入，从而丰富不同维度特征。因此，本文将一维旋转机械振动信号作为多特征融合CNN 网络模型中1D CNN 网络模型的输入，将从连续小波变换得到的小波时频图作为多特征融合CNN 网络模型中2D CNN 网络模型的输入。图3 为原始振动信号（彩图扫OSID 码可见，下同），图4 为经连续小波变换后得到的小波时频图。

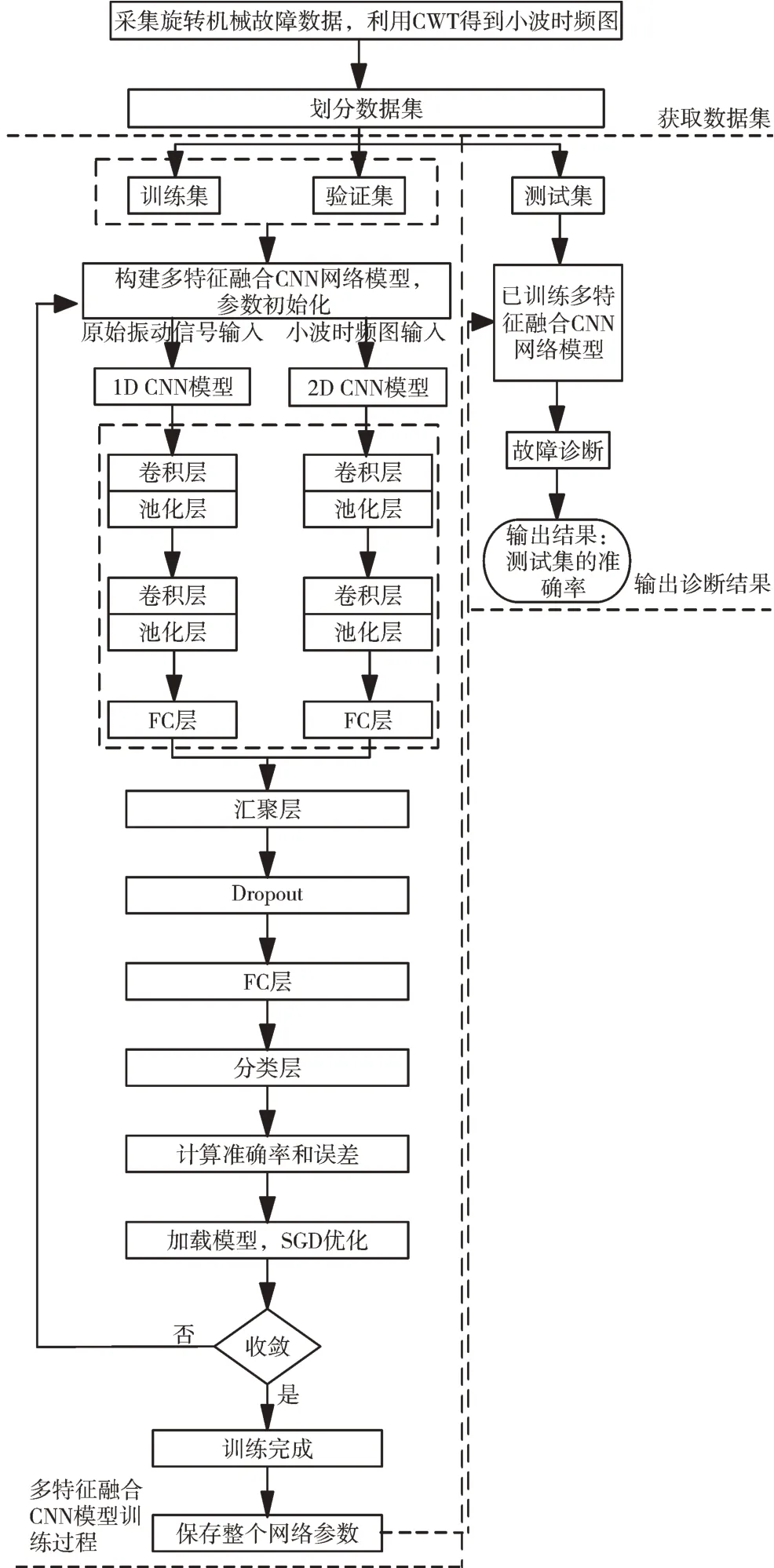
Fig.2 Method flow图2 方法流程

Fig.3 Original vibration signal图3 原始振动信号

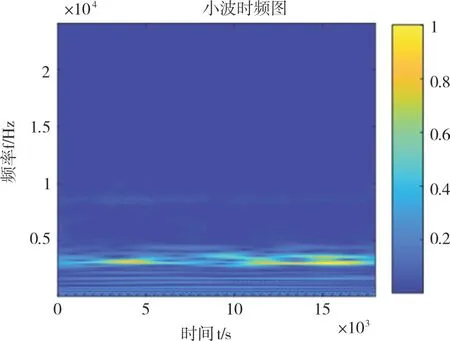
Fig.4 Wavelet time-frequency图4 小波时频

3.2 多特征融合CNN 网络模型训练过程

为了更好地利用一维原始振动信号和二维时频图融合和丰富两个不同维度特征，本文充分发挥CNN 的多特征融合优势，使用多特征融合CNN 网络模型作为轴承故障诊断模型，本文多特征融合CNN 网络模型结构如图5 所示。多特征融合CNN 网络模型中1D CNN 的输入是一维数组，所以在轴承故障诊断中可以直接输入原始的一维振动信号，而2D CNN 输入的是二维信号或者图像，所以需要对原始信号做一定的预处理将其转化为二维信号或者图像。

原始的一维旋转机械振动信号输入1D CNN 模型，经过输入层、卷积层、池化层、全连接层，得到拉伸后的一组特征向量；同时将原始的一维旋转机械振动信号经过连续小波变换后得到的小波时频图输入2D CNN 模型，同样经过输入层、卷积层、池化层、卷积、全连接层，得到另一组拉伸后的特征向量。将两组向量在汇聚层进行拼接，再经过Dropout 层、全连接层和分类层，最终得到不同旋转机械故障的分类。

4 实验与分析

4.1 实验数据

本实验数据集1 来自凯斯西储大学（CWRU）的轴承数据库。如表1 所示，数据的采集频率为48kHz，数据集包含不同的组件故障以及同一类但具有不同严重级别的故障，共10 种故障类别。其中，正常作为一类特殊的故障类型，其他依次为滚动体、内圈和外圈，分别为在损伤斑点0.007inches，0.014 inches，0.021 inches 三种直径下的故障模式。每类故障各有1 000 个样本，一共10 000 个样本。数据集按照7∶2∶1 的比例划分，即训练集7 000 个，验证集2 000 个，测试集1 000 个。

本实验数据集2 来自机械故障预防技术学会（MFPT）的轴承数据库。如表2 所示，输入轴速率为25Hz，采样速率为48 828sps。数据集包含不同的组件故障以及同一类但具有不同严重级别的故障，共14 种故障类别。每类故障各有1 000 个样本，一共有14 000 个样本。数据集按照7∶2∶1 的比例划分，即训练集9 800 个，验证集2 800 个，测试集1 400 个。

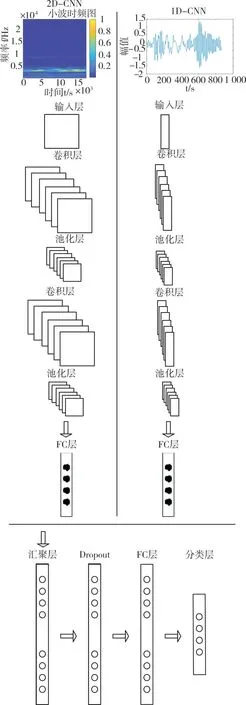
Fig.5 CNN network model structure with multi-feature fusion图5 多特征融合CNN 网络模型结构

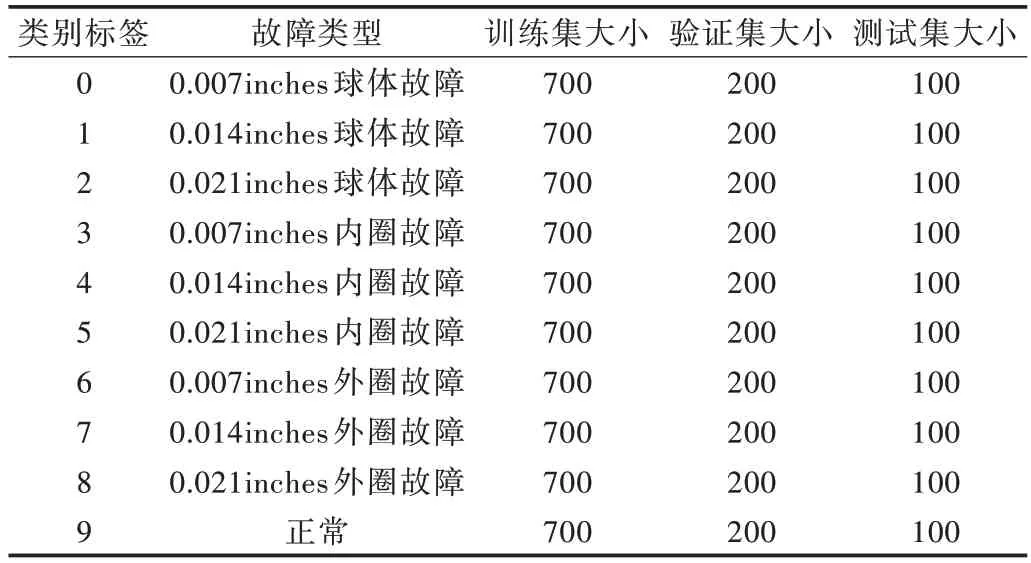
Table 1 Experimental data set 1表1 实验数据集1

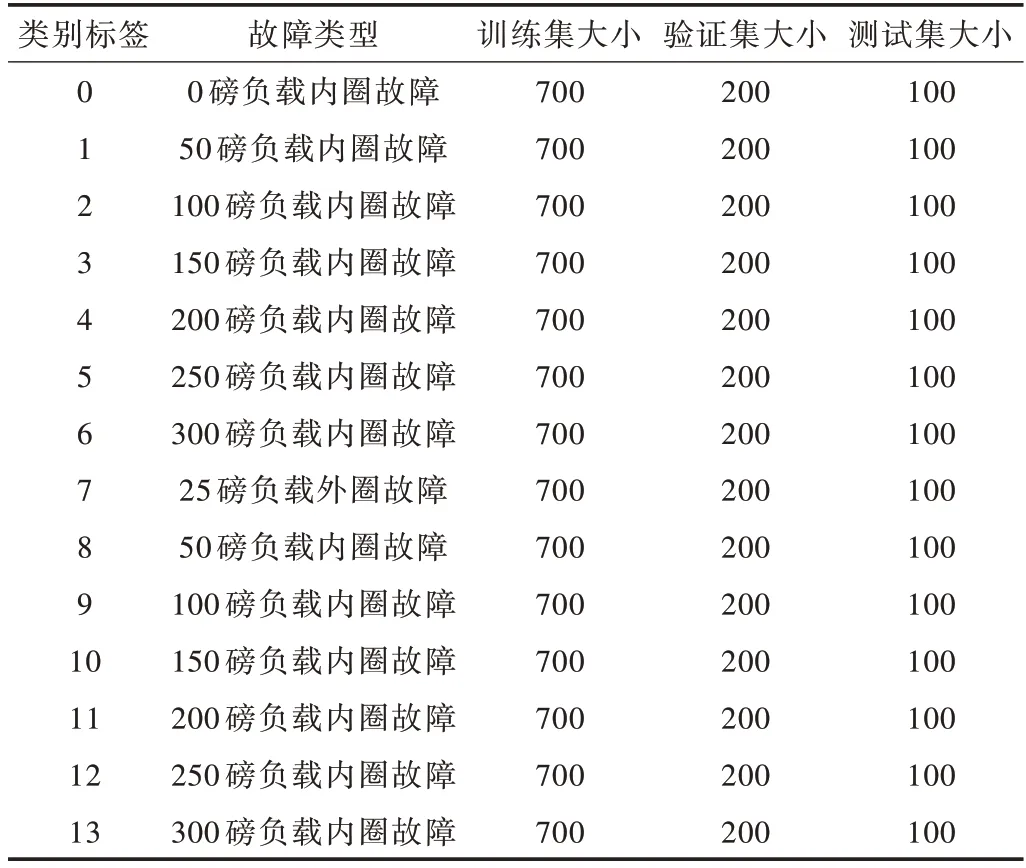
Table 2 Experimental data set 2表2 实验数据集2

4.2 实验环境及模型参数

本文实验环境基于Windows10（64 位），MATLAB R2014b，JetBrains PyCharm 2018.3 x64。

多特征融合CNN 网络中1D CNN 网络模型各层设置如表3 所示。模型共有2 个卷积层，第1 个卷积层有6 个卷积核，第2 个卷积层有16 个卷积核。多特征融合CNN 网络中2D CNN 网络模型各层设置如表4 所示。模型共有2 个卷积层，第1 个卷积层有6 个卷积核，第2 个卷积层有16 个卷积核。来自1D CNN 和2D CNN 模型的两组不同的一维特征向量，在汇聚层拼接成一个1×6112 的一维向量，然后经过Dropout 的随机失活，得到一个1×84 的一维特征向量，最终通过分类层得到一个1×10 的一维向量。网络采用Relu激活函数，模型的学习率为0.005，批处理大小为64，迭代次数为500 次。

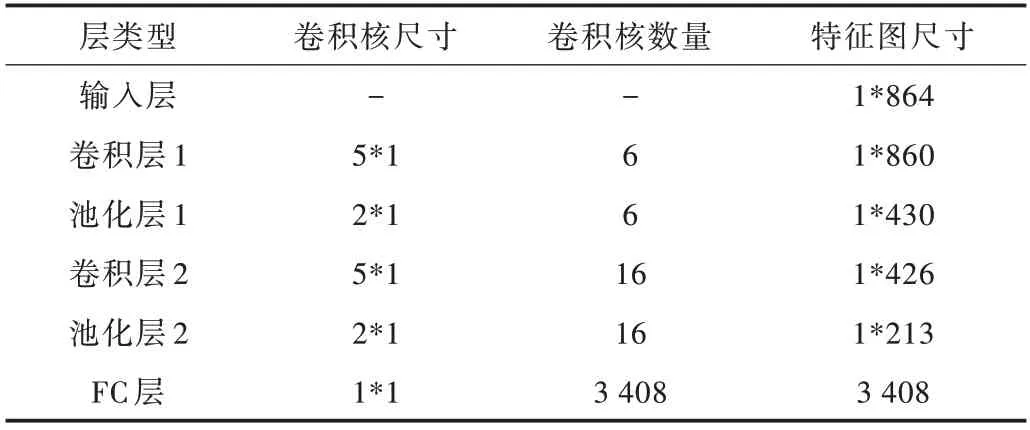
Table 3 1D CNN model parameters表3 1D CNN 模型参数

Table 4 2D CNN model parameters表4 2D CNN 模型参数

4.3 实验过程及结果分析

为验证本文提出的多特征融合CNN 网络模型的故障诊断准确率，将整个数据集分为训练集、验证集和测试集。首先，将训练集和验证集训练多特征融合的CNN 网络模型，然后将测试集输入已训练的多特征融合CNN 网络模型中并输出结果，得到测试集的准确率。

图6（彩图扫OSID 码可见，下同）显示训练集和验证集的故障分类诊断误差率。在前100 个迭代内，训练集的误差率和验证集的误差率下降相对较快，训练集的误差率从0.040 左右下降到0.016 左右，验证集的误差率从0.037 左右下降到0.013 左右。在第100 到200 个迭代内，训练集的误差率和验证集的误差率相对前100 个迭代下降变慢，训练集的误差率从0.016 左右下降到0.002 左右，验证集的误差率从0.013 左右下降到0.001 左右；在第200 到300 个迭代内，训练集的误差率和验证集的误差率下降相对平缓，训练集的误差率从0.002 左右下降到接近于0，验证集的误差率从0.001 左右下降到接近0。此后的迭代中，训练集和验证集的误差率都恒定在0 左右，表明此时的学习速率已经不再适合网络参数的继续优化，该网络模型迅速收敛。

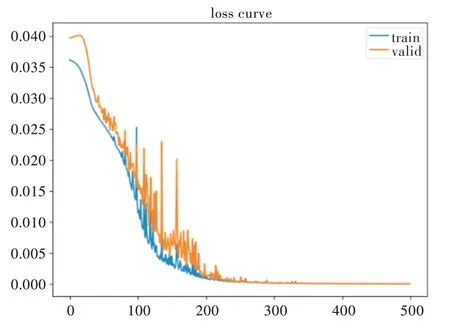
Fig.6 Error rate variation curve图6 误差率变化曲线

图7 为训练集和验证集的故障分类诊断准确率。在前100 个迭代内，训练集的准确率和验证集的准确率急速上升且波动较大，训练集的准确率从10%左右上升到83%左右，验证集的准确率从22%左右上升到82%左右。在第100 到200 个迭代内，训练集的准确率和验证集的准确率相对于前100 个迭代上升变慢，但波动依然很大。训练集的准确率从83%左右上升到99%左右，验证集的准确率从82%左右上升到97%左右；在第200 到300 个迭代内，训练集的准确率和验证集的准确率上升相对平缓，训练集的误差率从99% 左右上升到接近100%，验证集的准确率从97%左右上升到接近100%。此后的迭代中，训练集和验证集的准确率都恒定在100%左右，表明此时该网络模型的故障分类诊断正确率接近100%，网络模型已经训练完成，同时也证明了多特征融合CNN 网络模型有快速的收敛性和极高的故障诊断分类准确率。

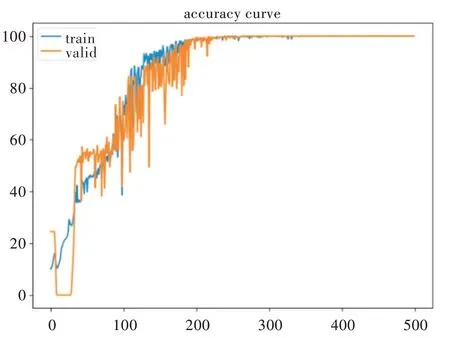
Fig.7 Accuracy change curve图7 准确率变化曲线

4.4 与其他方法对比分析

为进一步验证本文提出的多特征融合CNN 网络模型故障诊断的高准确率，选取离散傅里叶变换+1D CNN［22］和小波时频+2D CNN［23］进行对比实验分析。离散傅里叶变换+1D CNN 是原始时域振动信号通过离散傅里叶变换后得到的频域振动信号。用一维卷积神经网络进行训练以达到轴承故障分类诊断效果。小波时频+2D CNN 通过对轴承的振动信号进行连续小波变换得到小波时频图，将其作为特征图输入到二维卷积神经网络模型中训练以实现轴承故障分类诊断。分别采用上述3 种方法对数据集进行轴承故障分类诊断实验，表5 为各类故障诊断方法在相同数据集下的分类准确率。

Table 5 Fault diagnosis accuracy of different methods表5 不同方法的故障诊断准确率 （%）

从表5 可以看出，本文提出的多特征融合CNN 网络模型故障诊断分类准确率最终高达99.78%。与离散傅里叶变换+1D CNN 和小波时频+2D CNN 轴承故障诊断模型在相同数据集上的准确率相比，分别提升了9.67%、2.84%。各类方法的故障诊断结果对比表明，本文方法的测试准确率更高，更适合用于轴承故障诊断和分类。

5 结语

本文提出了一种多特征融合CNN 网络的旋转机械故障诊断模型，它将一维旋转机械振动信号、小波时频图和CNN 结合起来，利用CNN 的多特征融合特点丰富了两个不同维度的特征，进而提高了旋转机械故障诊断的准确率。首先通过连续小波变换将一维轴承信号转化为小波时频图，其次构建双流CNN 模型，其中，将一维轴承振动信号作为双流CNN 的1D CNN 输入，将小波时频图作为双流CNN的2D CNN 输入；然后训练网络模型；最后将测试集输入已训练的网络模型进行不同旋转机械故障的分类。与其他诊断方法相比，本文方法有更高的诊断准确率和较强的泛化能力，同时为轴承故障诊断分类提供了新的物理模型思路。但本文的实验数据集都是单个类型的，而在现实生产活动中旋转机械的故障往往是多个故障同时发生。因此，复合故障可以作为后续研究对象。此外，对于诊断模型本身而言，采用何种优化方法提高模型训练的收敛速度和效率值得研究。