基于KPCA-LightGBM 的心脏病预测研究
2021-09-28张云华
黄 嵩,张云华
(浙江理工大学 信息学院,浙江杭州 310018)
0 引言
根据世界卫生组织的报告,心脏病每年导致全球数百万人死亡[1]。引发心脏病的因素有很多,如工作压力过大和生活作息不规律等。中国作为世界人口第一大国,约有两亿多人患有不同程度的心脏病[2]。近年来,中国心脏病发病呈年轻化趋势[3]。与此同时,我国地区经济发展不平衡,公共医疗资源也严重不足。在这样的社会背景下,开发出一个能从病人的病历信息中筛选出有效信息,并协助医生作出心脏病诊断的算法具有非常高的现实价值[4]。
在国外,早在1976 年,斯坦福大学的Wraith 等[5]就开发出了MYCIN 系统,可以帮助医生对患者进行诊断,但由于早期的计算机计算性能有限,MYCIN 系统的准确性有限,功能也比较匮乏。近年来,随着机器学习的发展,可以通过计算机技术手段挖掘病人病历中的信息,在病历数据中找出疾病相关信息,并利用这些信息建立疾病预测模型[6]。苗立志等[7]使用支持向量机和随机森林实现了对乳腺癌的风险分析和预测;苗丰顺等[8]使用随机森林和XG⁃Boost 实现了糖尿病的风险预测;赵颖旭等[9]使用LightGBM对老年痴呆住院费用进行预测;Amin 等[10]使用支持向量机完成了对心脏病的预测。
本文基于已有研究,针对病历数据维度高的问题,首先对病历数据进行降维[11]。传统的主成分分析(PCA)方法是假设数据集中各特征是线性无关的,主要通过计算方差寻找不同特征之间的线性组合。而在很多应用场景下,线性映射很难得到想要的结果,核主成分分析(KPCA)通过核函数的思想获得了更好的特征提取性能。疾病诊断模型通常采用决策树实现,传统的决策树在高维稀疏的数据集上表现不佳,同时训练过程中只能串行训练,效率较低。针对该问题,本文采用LightGBM 算法,采用最优的策略分裂决策树的叶子结点,因此获得更高的精度[12]。
1 核主成分分析(KPCA)
主成分分析(PCA)是使用线性映射将数据进行降维,但是通常情况下高维到低维是非线性的,结果往往不尽人意。核主成分分析(KPCA)将原始数据通过选择适当的核函数(Kernel)映射到高纬度空间,再利用高维度空间进行线性降维,因此KPCA 的核心就是核函数[13]。
1.1 核函数
通过使用核函数,可以在低维度直接计算内积,避免将数据映射到高维后进行复杂计算[14]。即:
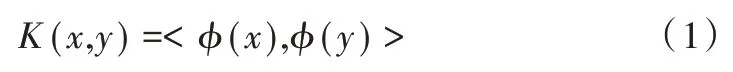
其中,x和y为低维的输入向量,φ是低维到高维的映射,
(1)线性核。只需在两个向量求内积上加个常数,只能解决线性可分问题:

(2)多项式核。相比于线性核多了指数d,因此可以处理非线性问题,要求a大于0,c大于0,适合所有训练数据归一化问题:
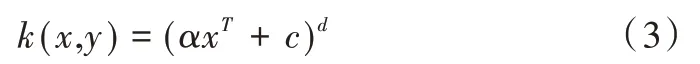
(3)高斯核。高斯核是沿径向对称的标量函数:
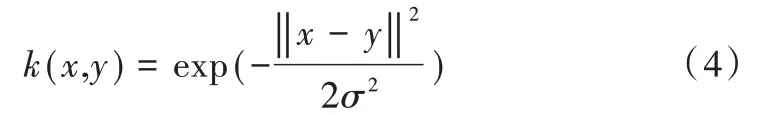
(4)指数核。与高斯核类似,将L2 范数变成L1。
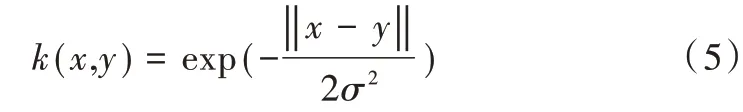
(5)拉普拉斯核。拉普拉斯核完全等价于指数核,但对敏感性降低。
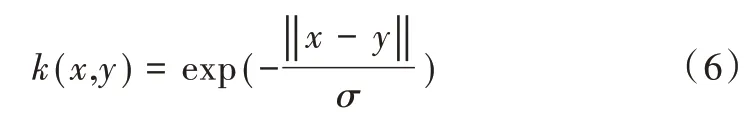
1.2 KPCA 原理
假设原始数据是如下矩阵X(数据每一列为一个样本,每个样本有m个属性,一共有n个样本)。
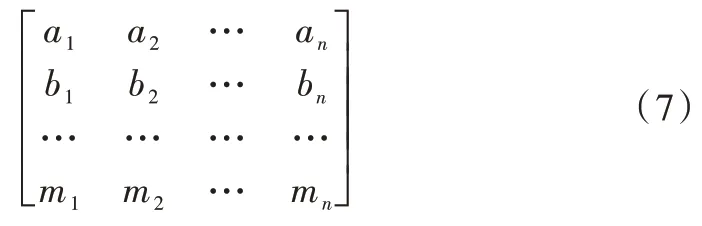
每个样本通过函数φ映射到高维空间,得到高维空间的数据矩阵φ(X)=φ(x(1))φ(x(2)) …φ(x(n)),x(i)是一个列向量。
用同样的方法计算高维空间中数据的协方差矩阵φ(x)φ(x)T,进一步计算特征值与特征向量(wi是特征值λi对应的特征向量):

根据维数的定义,空间中的所有样本可以线性表示出空间中的任一向量,因此可用所有样本表示特征向量:
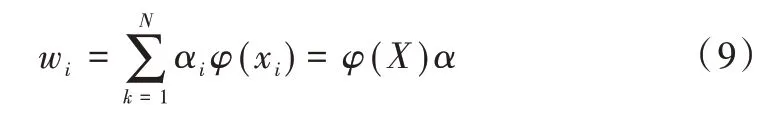
将这个线性组合代回到特征向量公式,替换特征向量,得到:
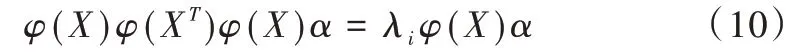
等式两边同时左乘φ(XT),得到:
令K=φ(XT)φ(X),原式变为:

φ(XT)φ(X)是如下矩阵,xi是一个列向量:
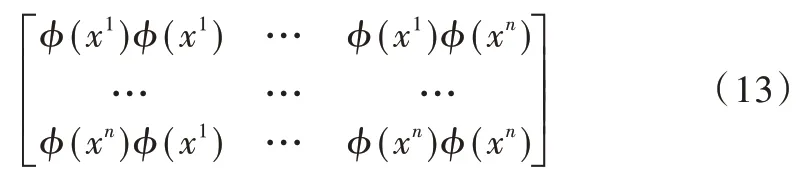
根据核函数的性质,上述核矩阵K可以直接在低维空间计算得到:
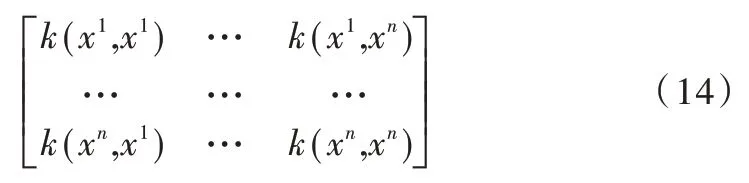
由于K是n维对称矩阵,所得解向量之间肯定是正交的,且最高可以达到n维。
2 LightGBM
LightGBM 是微软在2017 年开源的梯度提升框架[15]。经典的梯度提升决策树(GBDT)不能以小批次的形式训练模型,若需要提高训练速度,就需要将数据全部加载在内存中,但数据会受限于内存大小。LightGBM 通过基于梯度的单边采样(GOSS)、互斥特征捆绑(EFB)和Leaf-wise 的决策树生长策略,在单个机器不影响速度的情况下,尽可能多地提高训练效率,同时在多机并行时,尽可能降低通信代价[16]。
2.1 基于梯度的单边采样(GOSS)
传统的梯度提升决策树中,由于梯度大的样本对信息增益有更大影响,为了使上一次错分的样本点的权重增大[17],一般会直接抛弃梯度小的样本点,但这样会带来改变数据分布和损失模型精度等问题。LightGBM 通过基于梯度的单边采样(GOSS)则可以避免这两个问题发生,核心思想是对要进行分裂的特征的所有取值按照绝对值大小降序排序,然后重点关注训练不足的样本,而不会过多改变原数据集分布,具体算法如图1 所示。
2.2 互斥特征捆绑(EFB)
在实际应用中,高纬度的数据往往都是稀疏数据[18],并且许多特征往往都是互斥的。LightGBM 利用此特点,将某些特征的值重新编码,将多个特征捆绑成同一个特征,如图2 所示。
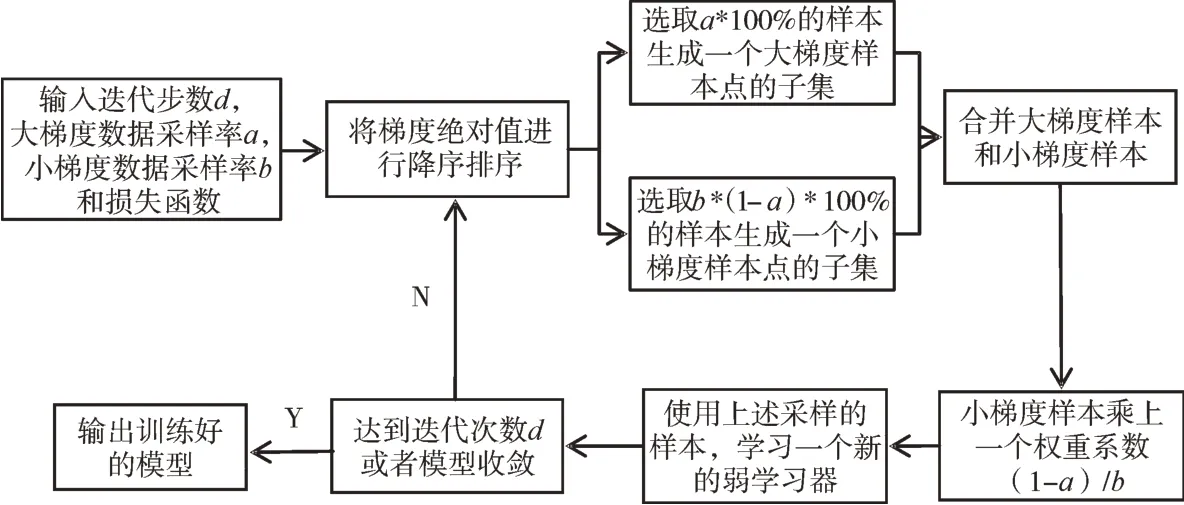
Fig.1 Description of the gradient-based one-sided sampling algorithm图1 基于梯度的单边采样算法描述
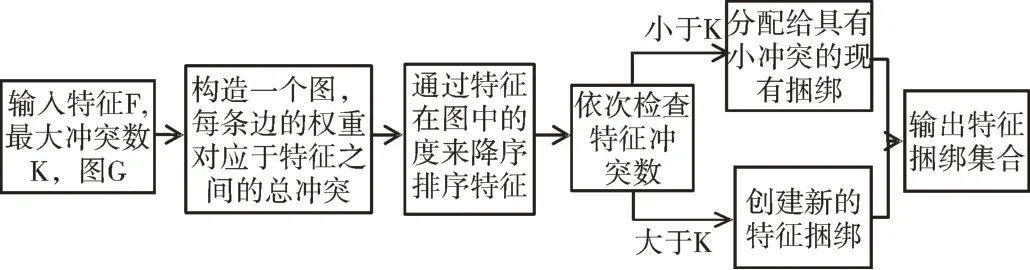
Fig.2 Description of the mutually exclusive feature bundling algorithm图2 互斥特征捆绑算法描述
在合并特征时,为了保证合并后在同一个bundle 里几个特征的原始特征值可以被识别出来,LightGBM 通过在特征值中加一个偏置常量来解决。如一个bundle 中有两个特征A、B,A 的取值范围为0~x,B 的取值范围为0~y,则可以在B 的取值范围上加一个偏置常量x,变为x~x+y,绑定后的bundle 取值范围为0~x+y,这样既可以将多个特征绑定在一个bundle 内,又可以有效地相互区分。
2.3 Leaf-wise 决策树生长策略
传统的梯度提升决策树如图3 所示,每一次分裂同一层的所有叶子,相当于对根结点进行广度优先遍历,这样会消耗大量时间和资源。
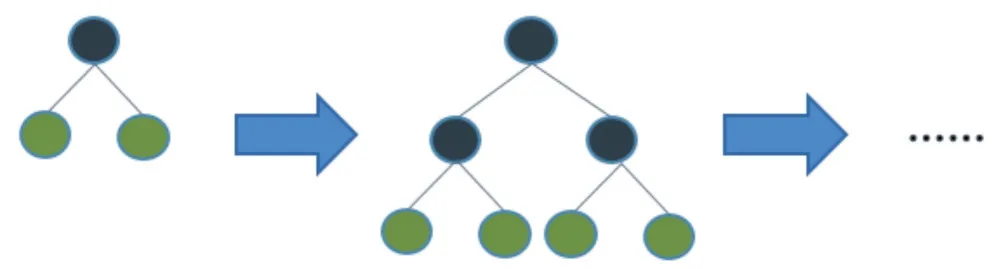
Fig.3 Traditional strategy growth tree图3 传统策略生长树
Leaf-wise 策略生长树如图4 所示,在每一层叶子结点分裂时,首先会找到最有训练价值的叶子结点,然后对其他叶子结点进行剪枝,这样在与传统策略生长树相同树高的情况下,消耗了更少的资源,同时能获得更高的精度。
Leaf-wise 在分裂时的增益公式为:
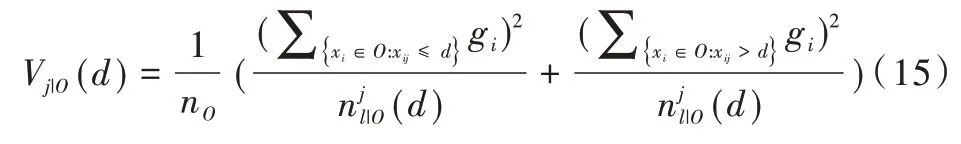
其中,gi代表损失函数关于第i个样本前T-1 轮拟合结果的负梯度,也即当前第T轮要拟合的目标值。
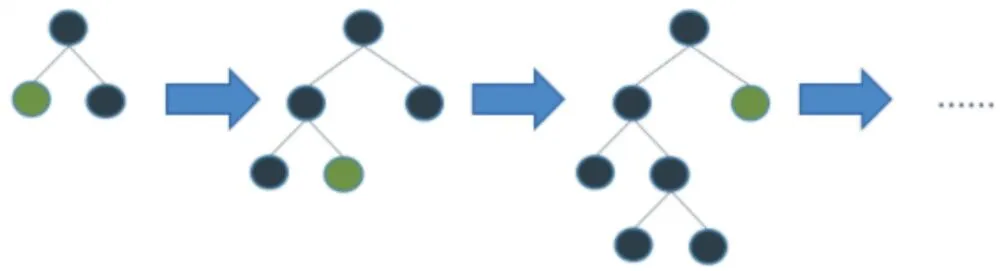
Fig.4 Leaf-wise strategy growth tree图4 Leaf-wise 策略生长树
对于当前结点而言,定义当前结点上样本集合为O,期望遍历所有候选特征及候选分裂点,找到一个特征j和对应的分裂点d,使得分裂当前结点后左右子结点上的样本总体方差更小,也即使得分裂之前结点的均方误差与分裂以后左右孩子结点的样本均方误差之和的差值最大。
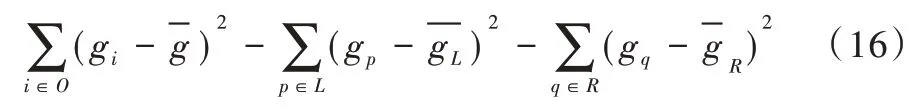
由于当前结点的均方误差对于当前结点分裂增益的计算是常量,因为:
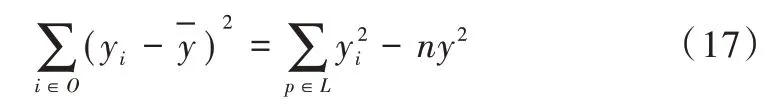
则可以将式(16)化简为:
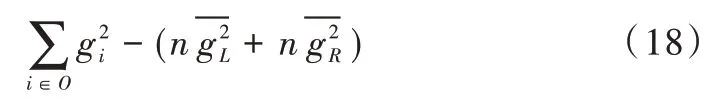
式(18)的第一项是常数,又因为:
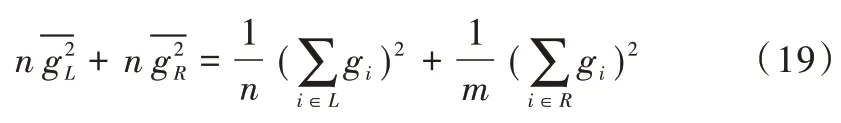
可以推出增益公式就是最大化左右叶子结点样本负梯度和的平方。
3 预测模型
本文所提出的KPCA-LighGBM 模型框架如图5 所示,首先对数据进行预处理,然后划分数据集,使用KPCA 算法对数据集进行降维后,使用降维以后的数据集训练LightG⁃BM 模型,最后使用训练好的LightGBM 模型预测结果,并通过与其他经典算法比较来评估KPCA-LighGBM 模型。

Fig.5 KPCA-LightGBM based prediction model图5 基于KPCA-LightGBM 的预测模型
(1)UCI 数据集。本文使用的数据集使用UCI 数据库中收集的克利夫兰心脏病数据集,这是机器学习研究人员在进行心脏病预测时常用的数据集[19]。数据集包含303 条记录,6 条记录有缺失值,将其从数据集中删除,共297 条有效数据。其中,137 份记录存在心脏病,160 条记录不存在心脏病数据集的具体字段如表1 所示。

Table 1 UCI cardiology dataset details表1 UCI 心脏病数据集详细信息
(2)数据预处理。数据预处理主要是将数据集转换成算法模型可以识别的数据[20]。UCI 数据集的大部分数据是文字,可以将其转化为数字以提高模型训练效率。数据集的数据有二值类的数据和多值类的数据。二值类的数据如status 字段,将buff 设置为1,sick 设置为0,其他二值类的字段以此类推。而多值类的数据如cp 字段,将typical、atyp⁃ical、non-anginal、asymptomatic 分别设置为0、1、2、3。其他多值类的字段也按此逻辑处理。
(3)数据集划分。本文采用交叉验证方式,将数据集进行切分,组合成不同的训练集和测试集[21]。多次重复该举动,可以得到多组不同的训练集合测试集,某次训练中的测试集可能成为另一次训练中的训练集。
(4)KPCA 降维。原始数据集中影响心脏病结果的特征值有13 个,然而并非所有特征值都与心脏病预测结果关联性很强,本文采用核主成分分析(KPCA)降维,通过属性合并创建新的属性,或者是删除相关性不高的属性,以提取最有价值的特征,降低运算成本。
(5)LightGBM 模型训练。将KPCA 降维过的训练集输入LightGBM 模型中进行训练,得到训练好的KPCA-Light⁃GBM 模型。
(6)结果预测。使用训练好的KPCA-LightGBM 模型对测试集进行检验,通过准确率、敏感度、精确度、特异度等指标对模型训练效果进行评估,并将结果与朴素贝叶斯、逻辑回归、随机森林、梯度提升树等经典分类算法作比较。
4 实验及分析
4.1 实验环境
实验硬件环境为:处理器为intel CORE i5-7400 CPU,NVIDIA GTX1050 4GD5 GPU,16G 内存,Windows10 64 位系统。实验软件环境为:Python 3.6.8 版本,PyCharm Profes⁃sional 2020.2 集成开发环境。
4.2 评价指标
根据数据集实际患病情况和KPCA-LightGBM 模型所预测出的患病情况,可将预测结果分为4 种:True Positive(以下简称TP)、True Negative(以下简称TN)、False Positive(以下简称FP)、False Negative(以下简称FN)。评价模型性能通常是比较以下属性:
准确率为模型总体判断准确率,如式(20)。
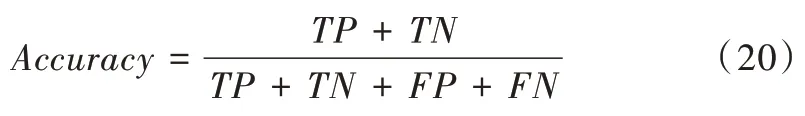
敏感度为在所有真实结果为正的数据中,预测出正值的比例,如式(21)。
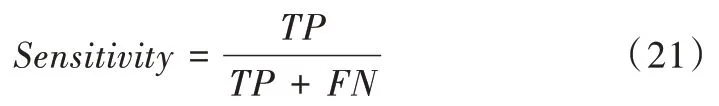
精确度为正向预测中预测出正值的比例,如式(22)。
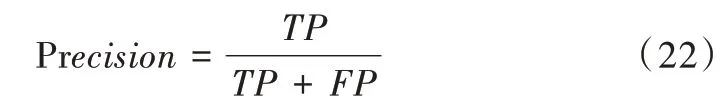
特异度为在所有真实结果为负的数据中,预测出负值的比例,如式(23)。
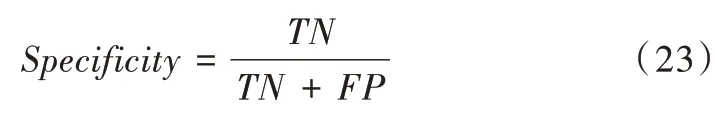
4.3 实验结果
本文将KPCA-LightGBM 模型和经典算法进行比较如表2 所示。与朴素贝叶斯、逻辑回归、随机森林、梯度提升树这些经典分类算法相比,本文提出的KPCA-LightGBM 模型准确率(Accuracy)达90.1%,较传统方法均有所提升。虽然在敏感度(Sensitivity)方面表现一般,但其在精确度(Pre⁃cision)方面与梯度提升树并列最好。同时,在特异度方面(Specificity),KPCA-LightGBM 模型达92%,显著领先于其他算法。特异度在医疗领域是一个非常重要的指标,如果该指标偏低,虽然不会引起漏诊情况,但是会大大增加医生负担和造成患者不必要的麻烦,同时还会造成目前紧张公共医疗资源的浪费。因此,综合各指标可以得出结论,KPCA-LightGBM 比其他算法预测效果更好。
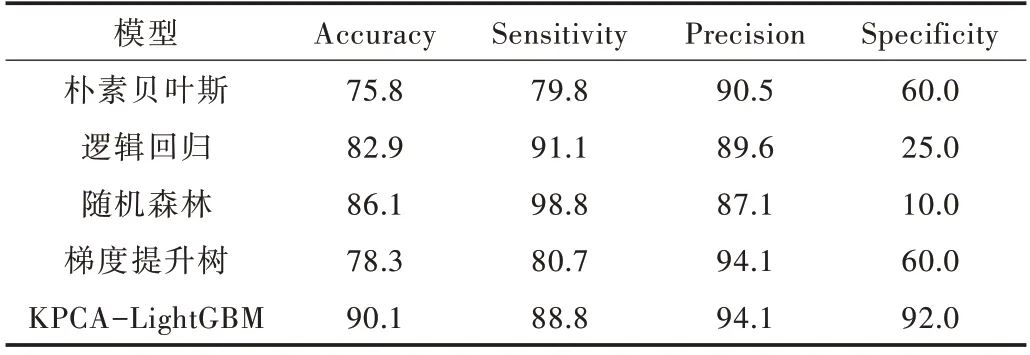
Table 2 Results from different models表2 不同模型的结果 (%)
5 结语
针对目前心脏病的高发病率,本文提出了一个KPCALightGBM 模型,用于帮助医生进行心脏病预诊。首先通过数据预处理从病历中提取信息,然后使用核主成分分析进行数据降维,再使用LightGBM 算法进行心脏病预测。实验表明,本文提出的KPCA-LightGBM 对心脏病预测的准确率优于经典算法;同时,KPCA-LightGBM 对特异度方面的性能明显优于其他算法,这可以避免对健康病人的误诊,减少患者负担,提高医生检查效率,从而缓解目前医疗资源不充足和发展不平衡问题。
本文提出的KPCA-LightGBM 模型目前仅用于心脏病预测,在后续研究中,可以通过增加数据集和优化模型结构的方法,进一步提高模型准确率,并让该算法可以预测更多疾病。
