双渠道多级分销网络库存整合优化配置

林瀚盛，屈 挺，徐素秀，THÜRER Matthias，郭洪飞，黄国全,4

(1.暨南大学 管理学院，广东 广州 510632；2.暨南大学 智能科学与工程学院，广东 珠海 519070；3.暨南大学物联网研究院，广东 珠海 519070；4.香港大学 工业与制造系统工程系，中国 香港 999077)

随着电子商务的蓬勃发展，快消品行业中的实体零售企业在保留原有线下销售渠道的同时相继“触电”——建立线上销售渠道，形成双渠道销售模式。在实际双渠道多级分销网络运作模式中，这些企业对双渠道库存和线上订单采取以下管理方式。1) 独立配置线下库存与线上库存；2) 线上订单由距离顾客最近的分销网络节点满足。虽然这样做能为企业带来管理上的便利，快速响应线上需求，但由于分散配置资源难以发挥规模效应，造成企业分销网络运作/库存成本居高不下，特别是对于分销网络终端门店而言。因此，企业希望对双渠道库存进行整合配置并集中履行线上订单以降低整体费用。

随着双渠道销售模式的兴起，渠道整合问题引起学者的关注。Xia等[1]和Herhausen等[2]证明线下渠道与线上渠道整合会带来竞争优势和渠道协同效应。Bendoly[3]研究双渠道销售下的线上线下库存共享的效应。Liu等[4]考虑双渠道库存系统的风险汇聚效应与运输成本之间的权衡问题。此外，学者也关注线上订单履行问题。Agatz等[5]回顾线上订单履行与多渠道分销的相关研究，认为线上订单履行对零售供应链管理研究很重要。Scott等[6]和Bretthauer等[7]分析线上订单分别由商店、中心仓库履行的情形。Alptekinoğlu等[8]在一个两级分销网络中，建立随机需求条件下的分销网络系统总成本最小化模型，阐述线上订单由某一层级节点履行的更优条件。Alawneh等[9]考虑线上订单由仓库履行的情况下，研究在仓库容量约束、需求和交货期不确定性条件下的多项目库存配库存模型。郑鑫等[10]研究线上库存在多个层级间分配的双渠道多级分销网络库存优化配置方法。

然而现有相关文献鲜有将渠道整合和线上订单履行问题结合起来，以在一个具有多层级、多节点的双渠道分销网络中研究库存集成优化配置问题。在实际的双渠道多级分销网络运作模式中，各节点均设有满足线下需求或向下游分销的线下(分拨)库存和满足线上需求的线上库存；同一线上订单可以由不同节点履行。因此，管理者在配置节点库存时要考虑线上订单履行问题以实现企业分销总运作成本最低。针对以上研究空白和管理挑战，本文拟综合考虑渠道整合和线上订单履行问题，研究在“双渠道库存独立管理、线上订单分散履行”和“双渠道库存整合管理、线上订单集中履行”2种不同分销网络运作模式对总运作成本的影响。

1 问题描述和符号说明

1.1 问题描述

考虑由单个中心仓、多个区域仓与多个门店组成的双渠道多级分销网络系统。该分销网络具有3个特点：1) 分销网络中的中心仓、区域仓和门店为同一企业所拥有，各层级节点都持有库存，皆具有对直接下级节点补货和对线上需求进行发货的功能，当库存不足而导致顾客需求(线上或线下)缺失时，会产生缺货惩罚成本；2) 线上需求由电商平台统一收集，再决定如何履行线上订单；3) 分拨库存用于满足下游节点发出的补货请求，线下库存用于满足顾客光临门店时产生的线下需求，线上库存用于满足电商平台分配的线上订单，线下需求只能由门店节点满足。

图1表示双渠道多级分销网络运作模式1，在该模式下节点内“双库存”由不同的管理者采取独立的库存控制策略所管理，分拨库存只用于满足下游补货需求，线下库存只用于满足线下需求，线上库存只用于满足线上需求。同时，各节点只满足其服务范围内的线上需求，即电商平台按照距离顾客最近的原则对线上订单进行分配，没有考虑集中履行线上订单。图2表示双渠道多级分销网络运作模式2，将原有的“双库存”进行整合配置，整合后的库存皆可用来满足线下(分拨)需求和线上需求，由管理者采取统一的库存控制策略所管理；节点服务范围内的线上需求可由直接高层节点来满足，即电商平台按照成本最小原则集中履行线上订单，将原本由低层节点响应的线上订单分配到直接高层节点。

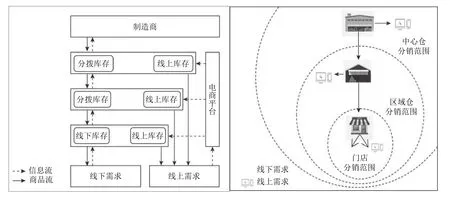
图1 双渠道多级分销网络运作模式1Figure 1 Dual-channel multi-echelon distribution network operation mode 1

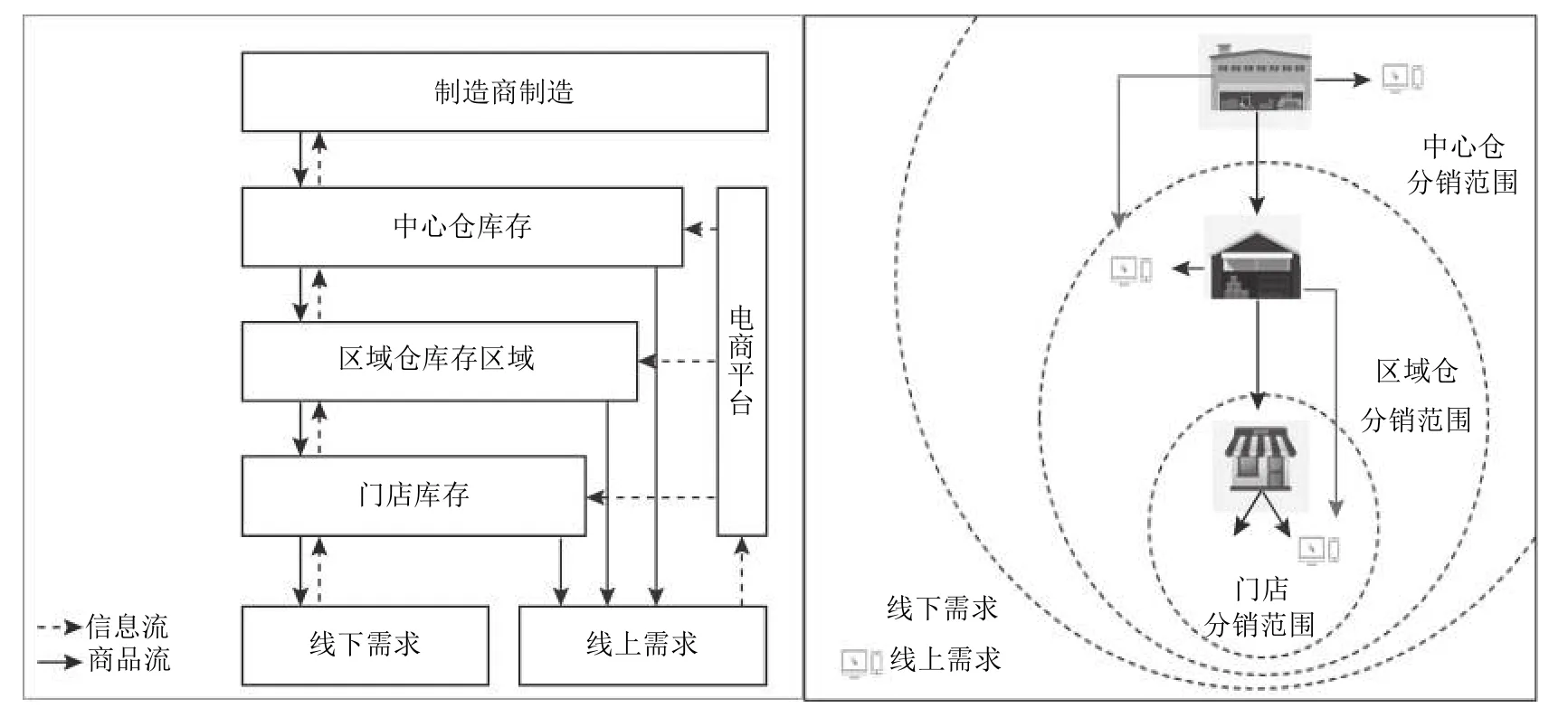
图2 双渠道多级分销网络运作模式2Figure 2 Dual-channel multi-echelon distribution network operation mode 2

因此，本研究着重解决2个问题：1) 如何通过科学的方法确定将原本由低层节点响应的线上订单分配到直接高层节点的数量；2) 如何在线下需求与线上需求并存条件下，构建合理的库存优化配置模型。

1.2 符号说明与基本假设

本文所用数学符号及其含义如表1。并假设如下。

表1 数学模型参数符号Table 1 Parameters of mathematical model

1) 单个区域仓 j 节点为 n′个门店节点提供库存补给，单个中心仓 o节 点为 m′个区域仓节点提供库存补给。

2) 各节点线下、线上需求随机，服从正态分布，单位时间内的线下线上需求均值µa,1、 µa,2和方差已知；其中区域仓、中心仓节点的线下需求指其直接下游节点的线下需求与线上需求之和。

3) 门店节点的线下库存量取决于其线下需求，区域仓和中心仓的分销库存量取决于其直接下游节点的线下需求与线上需求。

4) 补货提前期 La是随机变量，服从正态分布

5) 所有节点均采用连续性盘点的(Q, R)库存策略。

6) 门店节点的补货需求由区域仓节点响应，区域仓节点的补货需求由中心仓节点响应。

7) 中心仓的库存容量不受限制，区域仓与门店的库存容量有限。

8) 系统允许缺货，各节点服务范围内的单位顾客需求不能即时满足时，顾客需求便损失，则在其相应的节点计算一次缺货惩罚成本，但系统内上下层级之间的缺货不计算缺货惩罚成本。

2 模型建立

对分销网络2种不同的运作模式分别建立数学模型1与数学模型2。数学模型均由3个层级的库存持有成本、库存订货成本、线上需求配送成本和缺货惩罚成本组成，优化目标皆追求总成本最小化。模型1与模型2的不同之处如下。1) 是否对节点内的“双库存”进行整合管理。模型1针对“双库存”独立管理的情形，节点的线上库存与线下库存/分拨库存由不同的管理者所控制，采取独立的库存控制策略，节点内的“双库存”不能互补；模型2针对于“双库存”整合管理者的情形，将节点内的“双库存”进行整合，由同一管理采取统一的库存控制策略，节点内的“双库存”能够进行互补。2) 是否考虑将低层级节点服务范围内的线上需求由高层级节点进行发货响应。模型1不考虑将低层级节点服务范围内的线上需求由高层级节点进行响应，模型2则相反。

双渠道多级分销网络运作模式1的库存成本模型(简称为模型1)建立过程如下。

区域仓 j 节点单位时间的线下需求均值、方差分别为

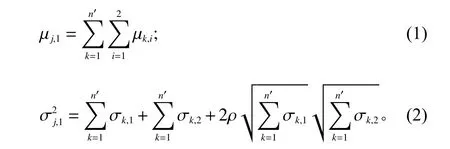
其中，n′表 示单个区域仓 j节点所服务的门店数量。

中心仓 o节点单位时间的线下需求均值、方差分别为

其中，m′表 示单个中心仓o 节点所服务的区域仓数量。

节点 a补货提前期 La内 的需求量 DLa,i近似服从，其中

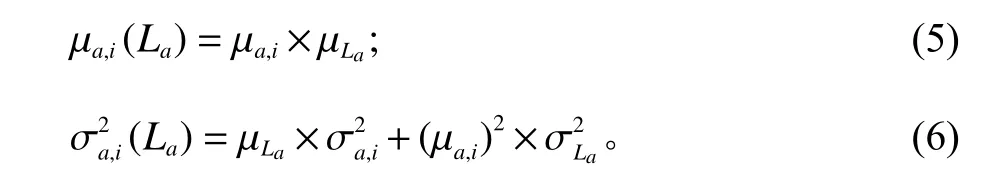
节点a 订货点为

由于节点 a采取连续盘点(Q, R)策略，故缺货只可能在补货提前期内发生，令表示节点 a补货提前期内i需求的缺货量，则

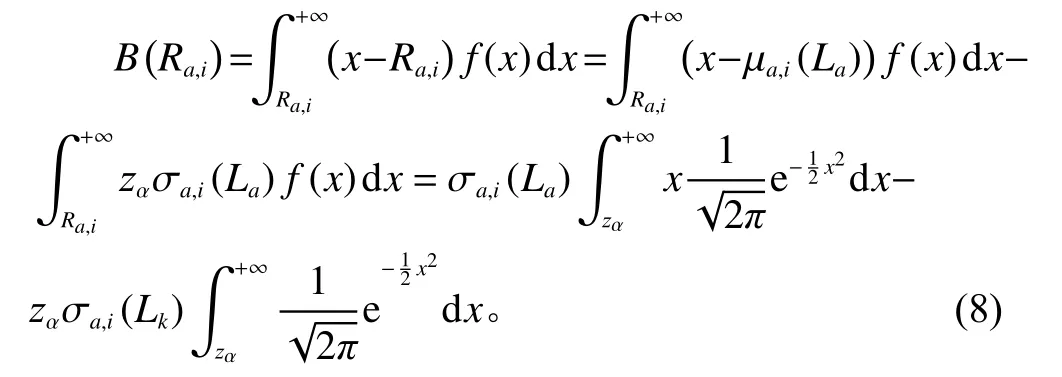
令节点a 的 i需 求订货量为 Qa,i，则其补货周期为

节点a 每个周期内期初库存量为Qa,i+Ra,i−µa,i(La)，期末库存量为 Ra,i−µa,i(La)，则其周期内平均库存量为节点 a周期内库存持有成本CHa,i、订货成本C Pa,i、 线上需求配送成本C Fa,i和缺货罚款成本C Ba,i分别如下。

人类的工业活动影响了地震活动。20世纪80年代末，荣昌天然气田采气时，污水由数口废井(深度在2～3km之间)导入地下，不仅如此，地震活动不断增多。随后，该地注水诱发地震活动受到大量学者高度重视[1-3]。

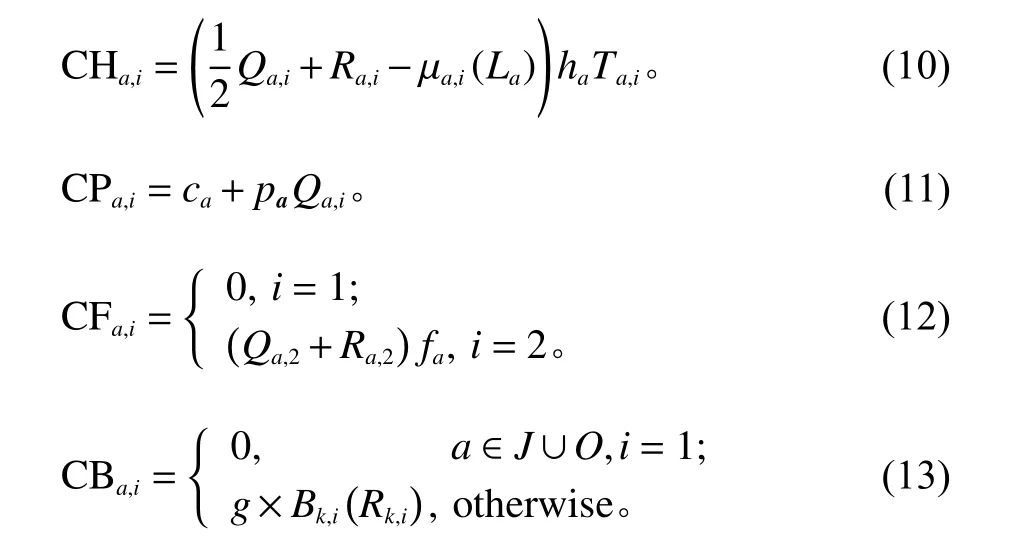
节点a 单位时间内的库存总费用为

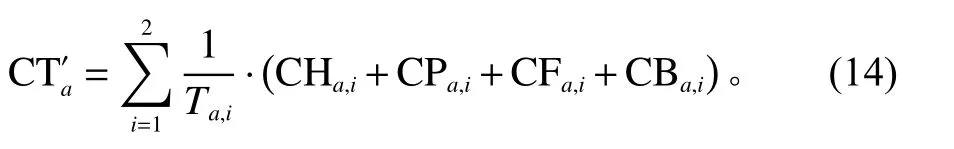
因此，综合以上所有的公式，将获得系统内单位时间库存总费用 CT′的数学模型，建立的目标函数为

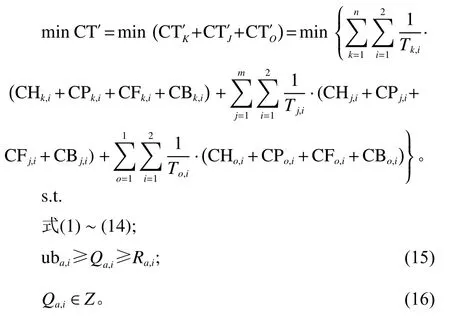
在双渠道多级分销网络运作模式2的情形下，管理者整合管理节点内的线下和线上需求，并且就线下库存/分拨库存的补货数量和线上库存的补货数量统一向上层节点发出补货申请。同时各节点内部的库存数量不仅受到其服务范围内的需求数量影响，还受到节点自身转移出去的线上需求数量的影响，或者受到接收来自下级节点往上转移的线上需求数量的影响。模式2下库存成本模型(简称为模型2)建立过程如下。

门店k 节点单位时间内的需求均值µk与 方差为

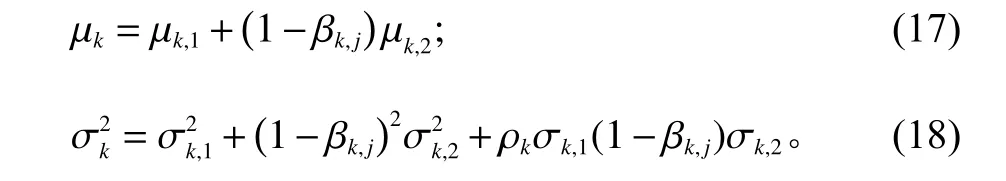
区域仓 j 节点单位时间内的需求均值 µj与方差为

中心仓o 单 位时间内的需求均值µo与 方差为

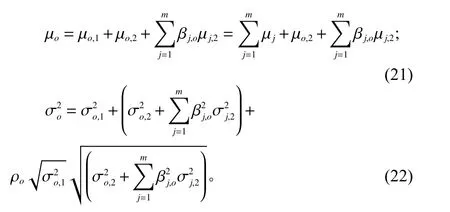
令 B (Ra)表 示节点a 补货提前期内的缺货量，则

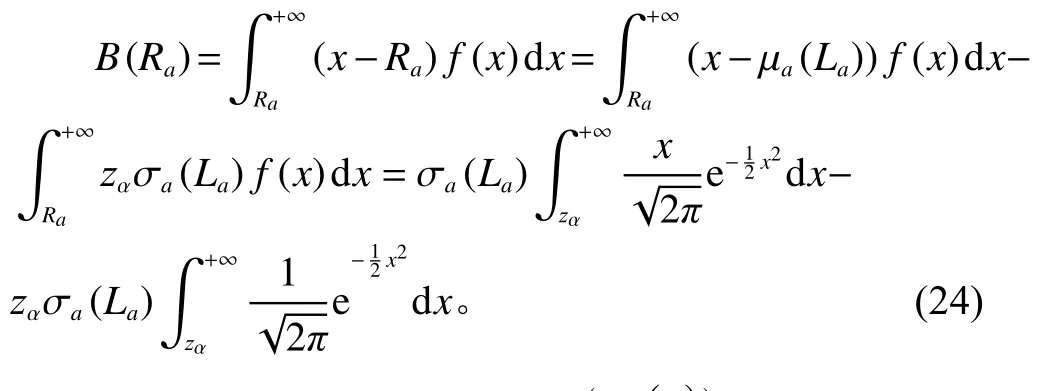
令节点 a的订货量为 Qa，则其补货周期Ta=Qa/µa。 节点 a每 个周期内期初库存量为 Qa+Ra−µa(La)，期末库存量为 Ra−µa(La)，其周期内平均库存量为节点a 周 期内库存持有成本C Ha、订货成本 C Pa、 线上需求配送成本 C Fa和缺货罚款成本CBa分别为

节点a 单位时间内的库存总费用为

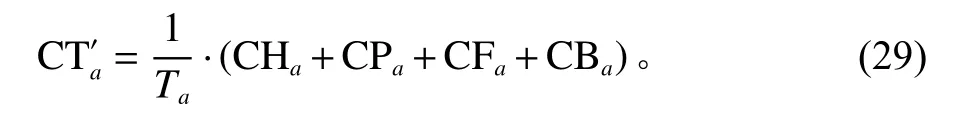
因此，建立的目标函数为

3 模型求解

本文所建立的库存成本模型是非线性整数规划模型，属于NP难问题，故采用遗传算法来求解，采用的编码方式为实数编码。具体求解步骤如下。

步骤1染色体编码。假设该分销网络由单个中心仓、m个区域仓与n个门店组成。对于模型1而言，决策变量为 Qa,i，其数量共有 2(1+m+n)个，故模型1的染色体长度为 2 (1+m+n)；然后让每个基因在[Ra,i,U Qa,i] 之间产生一个随机整数，其中 U Qa,i代表Qa,i的上限(由节点的库存容量决定)。对于模型2而言，决策变量为 βa,b和 Qa，其数量分别有 ( m+n)个和(1+m+n)个 ，故模型2的染色体长度为 2(m+n)+1；然后让前 ( m+n)个基因在[0,1] 之间产生随机数表示βa,b具 体数值，让后 (1+m+n)个 基因在[Ra,U Qa] 之间产生随机整数表示 Qa具体数值，其中 U Qa代 表 Qa的上限。

步骤2产生初始种群。初始种群规模为50。

步骤3计算适应度。适应度的计算使用以下公式，可将最小值转化为最大适应度，其中Fmax(t)表示将种群中所有染色体代入模型后所得到的数值中最大值， Fi表示将第i个染色体代入模型后得到的数值，ε表示一个较小的大于0的随机数， F xi表示第i个染色体的适应度。

步骤4选择操作。采用轮盘赌法。

步骤5交叉。本文采用模拟二进制交叉[11]，交叉概率为0.8。假设2个父代个体和则使用SBX算子产生的2个后代个体可通过以下公式计算得到。

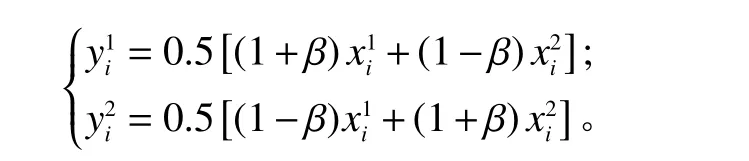
其中，β是由分布因子η 按以下公式动态随机决定的。

η是一个自定义的参数，η值越大则产生的后代个体逼近父代个体的概率越大，本文取 η=1。 rand表示(0，1)之间产生随机数。

本文通过以下公式保证交叉操作后得到的后代个体符合模型约束条件。

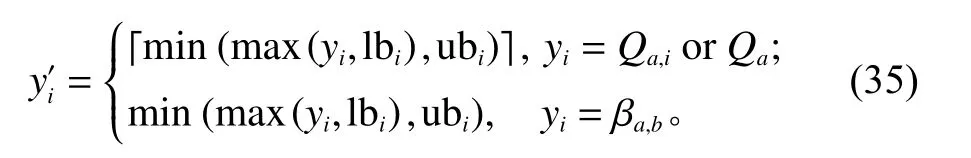
其中， lbi、 ubi分 别表示基因 yi的下限与上限，表示向上取整。

步骤6变异。本文采用多项式变异[12]，变异概率为0.05，具体计算公式为

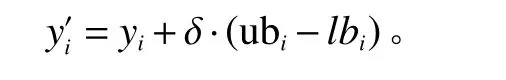
其中，

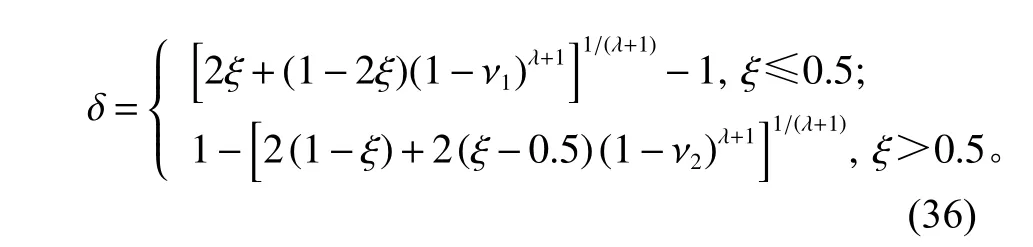
ξ表示(0,1)之间产生随机数，ν1=(yi−lbi)/(ubi−lbi)， ν2=(ubi−yi)/(ubi−lbi)， 取λ =1。

通过式(35)保证变异操作后得到的后代个体符合模型约束条件。

步骤7算法终止。当算法迭代次数达到最大时终止算法，迭代次数为100。

4 数值仿真

本文的数学模型及算法采用Python3.6实现，案例参数的设定参考我国某红酒企业的实际运作情况。为了简化运算，假设该分销网络由1个中心仓、3个区域仓与10个门店组成，如图3所示，具体参数设置如表2所示。通过对GA算法进行实现及运行求解，获得的配置结果如表3所示，表3记录了模型1和模型2的库存优化配置结果、分销网络各层级总成本及系统总成本。

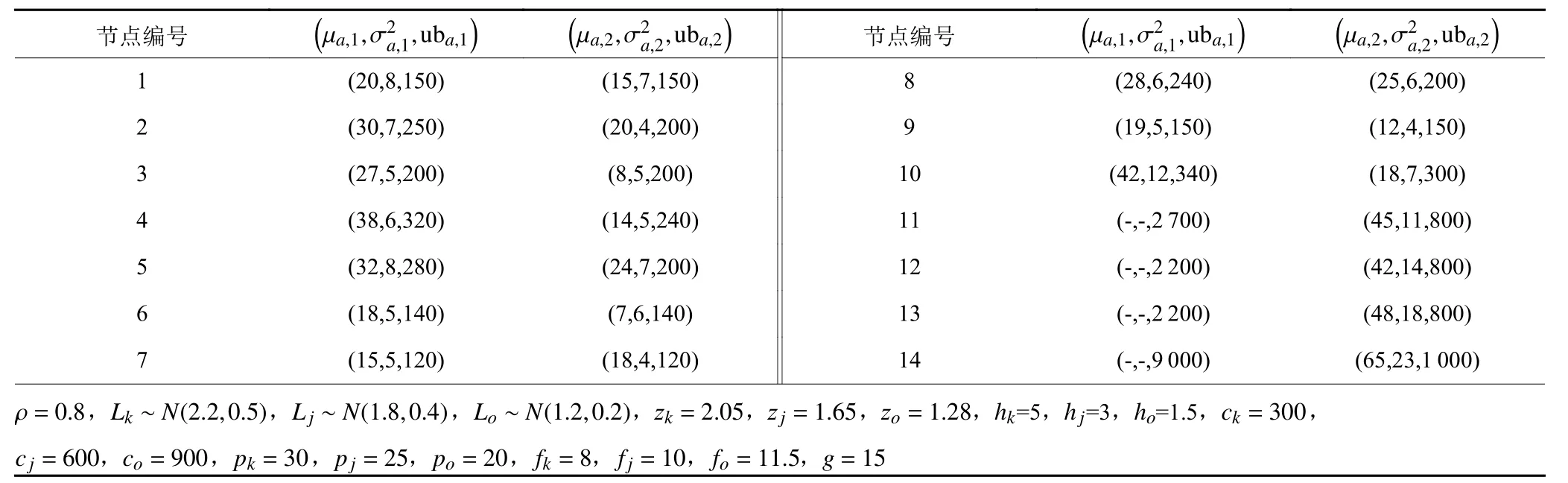
表2 案例具体参数设置Table 2 Parameters value of the instance

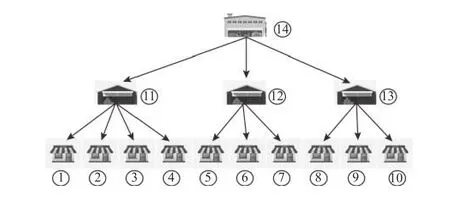
图3 多级分销网络的实例Figure 3 The instance of multi-echelon distribution network

在表3数据中可以看出，模型2的系统库存总费用为51 447.34，明显低于模型1系统库存总费用62 175.59，约减少17.25%。通过对比模型1与模型2各层级库存总费用，发现模型2门店层级库存总费用与区域仓层级库存总费用均低于模型1的与，而模型2中心仓层级库存总费用高于模型1的。这表明双渠道多级分销网络运作模式2与运作模式1相比，通过整合节点内的“双库存”由单个管理者采取统一的库存控制策略所管理，且将低层节点的线上订单分配到直接高层节点集中履行(模型2的βa,b等于1)，虽然提高了中心仓层级的库存总费用，但能够有效地降低门店层级和区域仓层级的库存总费用，进而使运作模式2下的系统库存总费用优于运作模式1。此外，在运作模式1下，分销网络中下游的库存总费用比上游的库存总费用高；而在运作模式2下，上游的库存总费用均高于中下游的库存总费用。这表明“双库存”整合配置和线上订单集中履行能够将库存总费用从中下游往上游转移，减缓中下游节点的库存总费用。

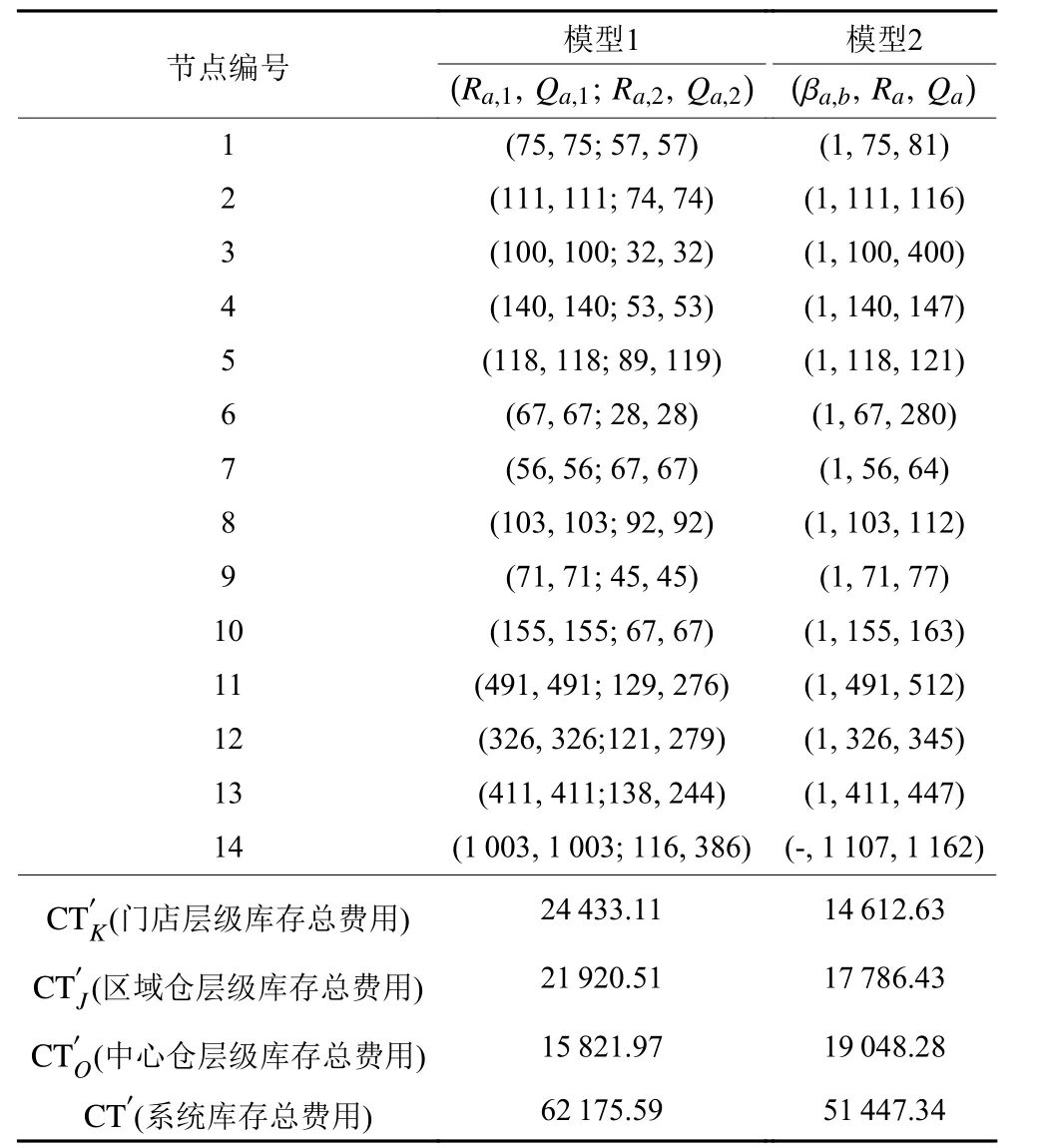
表3 案例优化配置结果Table 3 Results of mathematical model optimization configuration

为了进一步分析双渠道库存整合管理和线上订单集中履行对分销网络系统库存总费用的影响，在上述模型1和模型2求解结果的基础上进行一组关于需求波动率(标准差/均值)的敏感性分析，如图4。在实验中，通过改变各节点需求标准差进而增加需求波动率的倍数，分别将系统库存总费用增加额、门店层级库存总费用增加额、区域仓层级库存总费用增加额、中心仓层级库存总费用增加额作为实验结果。

从图4中可知随着需求波动率的增加，模型1和模型2的系统库存总费用皆呈现出上升的趋势，但模型2的系统库存总费用增加额一直低于模型1的系统库存总费用增加额。这表明在运作模式2下，双渠道库存整合管理和线上订单集中履行能够有效减缓需求波动率变动对系统库存总费用的影响。通过对比需求波动率增加对模型1与模型2各层级库存总费用的影响，发现门店层级库存总费用增加额均在模型1和模型2系统库存总费用增加额中占的比重最大，但相对于模型1而言，对模型2门店层级库存总费用的影响较小；然而，需求波动率增加对模型2区域仓层级库存总费用的影响比模型1的大。

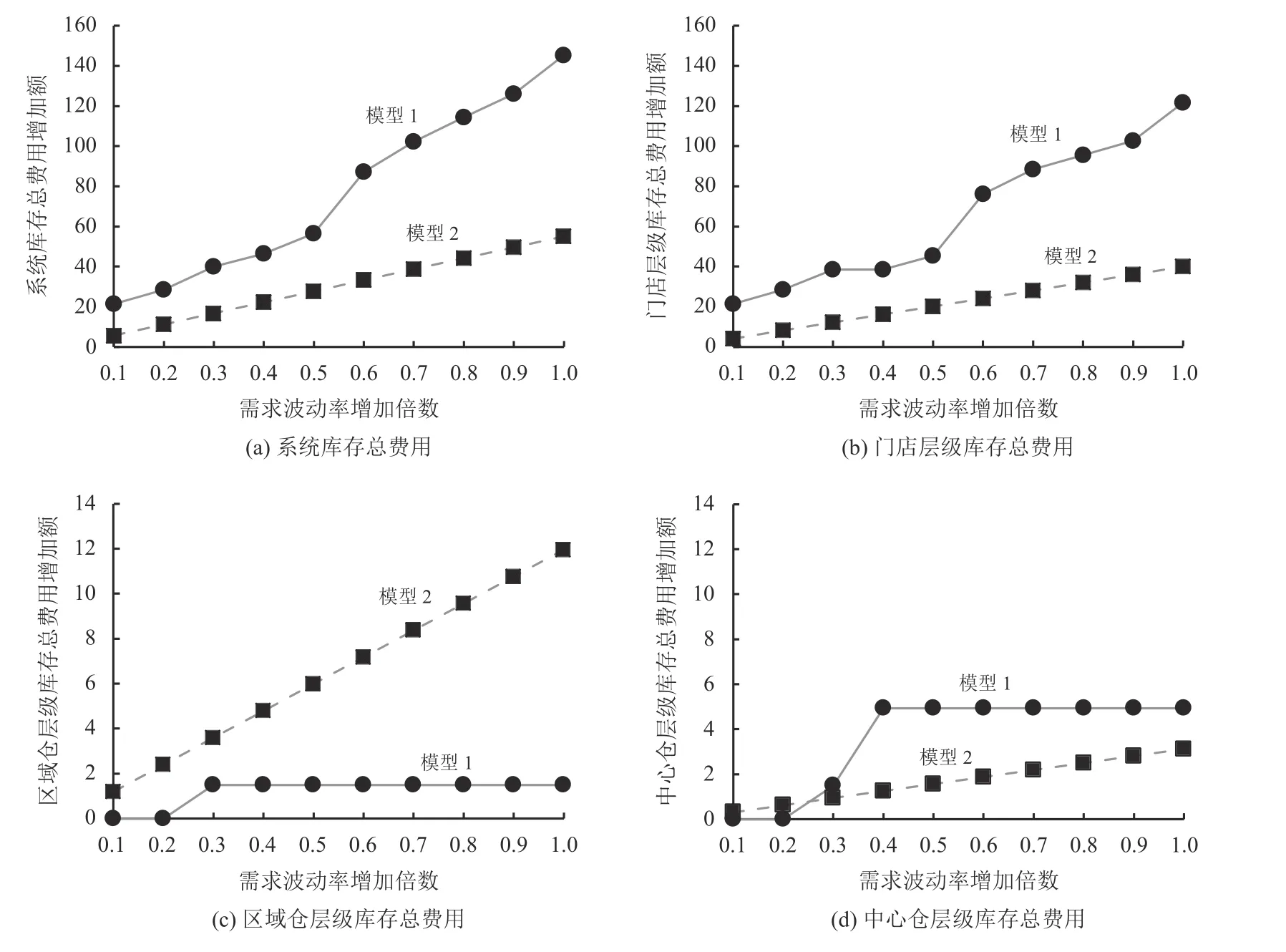
图4 不同需求波动率下的库存总费用变化Figure 4 Changes in total inventory costs under different coefficient of variation

5 结论

本文在一个由单一中心仓、多个区域仓和多个门店组成的双渠道多级分销系统中，分别在“双渠道库存独立管理、线上订单分散履行”和“双渠道库存整合管理、线上订单集中履行”这两种不同双渠道多级分销网络运作模式下建立库存优化配置模型，以研究渠道整合和线上订单履行对总运作成本的影响。然后设计了遗传算法并用Python3.6进行求解，通过数值仿真，得到的结论和启示如下。

1) 在双渠道销售模式下，渠道整合和线上订单履行显著影响双渠道多级分销网络的系统库存总费用。通过数值仿真验证了“双渠道库存独立管理、线上订单分散履行”和“双渠道库存整合管理、线上订单集中履行”两种不同情形下的系统库存总费用，发现后者可以显著降低整个网络的库存总费用。因此，在设计双渠道多级分销网络运作模式时，要同时将渠道整合和线上订单履行问题考虑进去，通过整合管理双渠道库存、集中履行线上订单，使得系统库存总费用达到最优。

2) 通过双渠道库存整合配置和将原本由低层节点响应的线上订单分配到直接高层节点由高层节点集中履行，能够将库存总费用从中下游往上游转移，减缓中下游节点的库存总费用。这能有效缓解双渠道销售模式下分销网络终端门店费用居高不下的困境。

3) 渠道整合和线上订单集中履行能够有效减缓需求波动率变动对系统库存总费用的影响，但需求波动率变动对分销网络中门店层级库存总费用的影响最大。因此，针对需求呈现出随机性、分散化特点的现状，对双渠道多级分销网络采取渠道库存整合和线上订单集中履行很有意义。

本文假设分销网络中所有节点均采取(Q, R)库存策略，且只考虑将线上订单向高层节点转移由高层节点集中履行，没有考虑线上订单由同层节点集中履行，未来的研究可以在这些方面的进行探索。