改进多种群遗传算法的AutoStore系统多AGV调度优化

王晓军，王 博，晋民杰，杨春霞，白新利

(1.太原科技大学 交通与物流学院，山西 太原 030024；2.山西海德拉太矿国际采矿刀具设备有限公司，山西 太原 030024)

AutoStore系统是一种新兴紧致密集型仓储系统[1]。如图1所示，该系统主体结构为铝制框架，每一列为一个货格。规格统一的料箱是基本存储单元，依次堆存在货格中。AGV小车四侧都有轮子，能通过货架顶层轨道实现前后左右4个方向的移动，同时小车底部有一个提升装置，能伸入货格内抓取或放入料箱。该系统属于“货到人”工作模式[2]，在执行出入库作业时，AGV小车将装有目标货物的料箱或空箱搬运至工作台，由工作人员拣选或放入货物后，再将料箱运回。因此，AGV调度是该系统的核心环节，对其进行优化研究，可提高作业效率，减少作业成本。

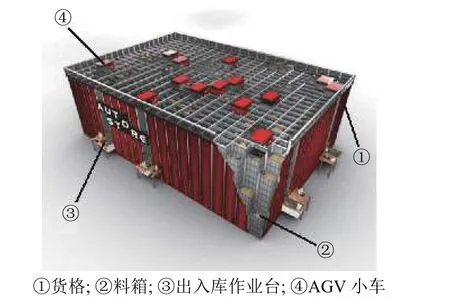
图1 AutoStore系统示意图Figure 1 Sketch map of AutoStore system

该新型仓储系统没有巷道，存储密度大，且拓展性强，近几年在欧洲出现后便迅速流行起来。但目前在国内还鲜有见到[1,3]，通过文献检索，也尚未找到针对AGV调度的学术研究。此处先根据出、入库作业模式对传统密集型仓储系统相关研究进行分析。

1) 出、入库单独作业模式。设置集中补货时间，期间只安排入库作业；其余时间根据订单进行出库作业[4]。该模式较为简单，根据订单任务按顺序进行即可，但AGV空载较多，会导致资源浪费。

2) 出、入库联合作业模式。杨玮等[5]在考虑AGV加减速运动的前提下，通过分析验证联合作业能降低AGV空载率。阚世奇等[6]为实现多层穿梭车系统的联合作业，提出一种存取订单序列匹配方法，以提高系统作业能力。刘高强等[7]针对生产车间多AGV任务分配问题，以作业时间最小为优化目标。李腾等[8]通过分析“货到人”拣选系统作业流程，提出在分批下发订单任务情况下的一种随机调度策略。崔敬伟[9]重点关注AGV动态分配问题，保证调度方案的可操作性。杨智飞等[10]考虑AGV调度的多目标性，优化目标包含作业完成时间、AGV配备数量及惩罚成本等三方面。Tavakoli等[11]研究工业系统中的AGV调度与分配问题，建立数学模型，并提出一种启发式算法进行求解。Miyamoto等[12]考虑有限冲突条件下的AGV任务分配问题，将其描述成一个整数规划，并提出局部/随机搜索方法。Liu等[13]建立自动仓储系统的AGV调度多目标模型，采用多种群自适应遗传算法进行求解，并证明其有效性。Fazlollahtabar等[14]考虑提前和延迟的惩罚，以保证得到无冲突任务分配方案。

上述研究尽管目的和思路各有不同，但从约束条件上大多具有如下特点：1) 出入库作业在同一平台进行，任务分配时通常将其视为一个点；2) 作业模式单一，为出入库单独作业模式或联合作业模式，一般情况下，联合作业时间要小于单独出入库作业时间之和。

AutoStore系统中，出入库作业台设置在货架最外围，且数量不唯一，此时情况要复杂得多。AGV可以在多个作业台工作，即起始点和终点不确定。以图2为例进行说明。图2为一个规模为10行10列仓储货架顶层，4个出入库作业台A1～A4分别布置在货架角落。

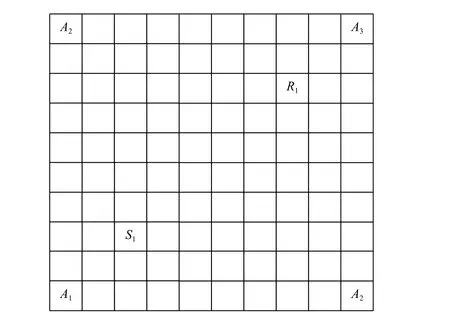
图2 出入库作业示意图Figure 2 Schematic diagram of warehousing operationm

设现有2个任务，一是需要将料箱存入货格S1，二是需要从货格R1提取料箱。采用单独作业方案时，需安排2台AGV，路径分别为：A1—S1—A1、A3—R1—A3，总路径长度为16格。若采用联合作业时，可只安排1台AGV：从A1搬运料箱至S1完成入库，空驶至R1，从R1搬运料箱至A3完成出库，总路径长度为18格。

从上述分析可知，AutoStore系统存在多个出入库作业台，联合作业时间并不一定小于单独作业时间。为提高作业效率，会出现单独出库作业、单独入库作业及联合出入库作业3种模式并存的现象，这使得传统研究方法无法适应该系统。

为此，本文将在作业流程分析基础上，综合考虑3种作业模式，建立总作业时间最小模型，并通过改进多种群遗传算法进行求解，最后利用算例进行分析和验证。本文研究将给AutoStore系统AGV任务分配及调度提供思路。

1 出入库作业流程分析

1.1 单独入库作业

1) 入库任务产生阶段。工作人员收到订单后，确定订单货物类别与数量。如已存有同类别货物，检查对应料箱是否有空余位置。如果有，直接确定入库料箱，如果存储空间不足则调用其余空箱，并确认存放位置。如果没有同类别货物，也调用空箱，确定存放位置。

2) AGV搬运目标料箱至入库工作台阶段。对当前任务，首先检索空闲状态AGV，并进行任务分配，如没有空闲AGV则等到有空闲AGV为止。对接到任务的AGV，首先移动至目标料箱顶部，若目标料箱上面还有其他料箱，需进行倒箱操作，即把目标箱上部的阻碍箱搬运至其他货格；当目标箱位于顶层时，将目标箱搬运至入库口放下。

3) 工作台操作阶段。工作人员在入库口接收目标料箱，将订单货物存入，并在系统确定目标箱存储位置。

4) AGV运回目标料箱阶段。再次检索空闲AGV并调用，将料箱运回原来货格。任务完成后，释放AGV。

1.2 单独出库作业

1) 出库任务产生阶段。与入库任务类似，工作人员将订单货物种类和数量与系统库存相比对，选择要提取的料箱，并确定为目标料箱。

2) AGV将目标料箱搬运至出库口。AGV调用与入库流程类似。

3) 工作台出库。工作人员从料箱中拣选所需货物，并确定目标存储位置。

4) AGV搬运目标料箱至目标存储位置，并更新系统相关状态。

1.3 联合出入库作业

联合作业则是根据订单顺序将出库和入库组合起来，可减少AGV空载时间。首先根据订单要求，将出库与入库匹配，对某一AGV而言，先执行入库订单，不用返回工作台，直接执行出库订单。其余步骤与出入库流程类似。

2 AGV调度任务分配优化模型

2.1 基本假设

1) AGV数量满足要求，不会出现无空余AGV可调用的情况；

2) AGV匀速行驶，考虑空载和负载速度差异，暂不考虑冲突；

3) AGV一次只能搬运一个料箱；

4) 订单任务无优先级，即不提前指定AGV执行任务的顺序。

2.2 考虑多作业模式的优化模型

设w 为工作台数目； n1、 n2分别为入库、出库任务数；v1、 v2分别为AGV空载和负载的行驶速度；对任务i， Bi为 需进行出入库任务的货位， Pi为出入库任务对应工作台位置， dPkBi为从目标工作台到目标货格的距离， dBiPk为从目标货格到目标工作台的距离，dBiBj为 i任 务货格到 j任务货格距离；对作业台k ， tRk、 tSk、 tCk分别是单独出库、单独入库及联合出入库作业时间。

决策变量 xik∈{0, 1}，当作业台k执行任务i时为1，否则为0；决策变量 yijk∈{0, 1}，从作业台k出发的AGV执行完任务i后转向作业台取值为1，否则为0。决策变量 zijk∈{0, 1}，当作业台k的任务i不是任务j的前置任务取值为1，否则为0。

模型建设分两步：首先分别建立单独出库、单独入库作业和联合出入库作业的模型；其次将三者相加，形成总作业时间模型。

1) 单独出库作业。

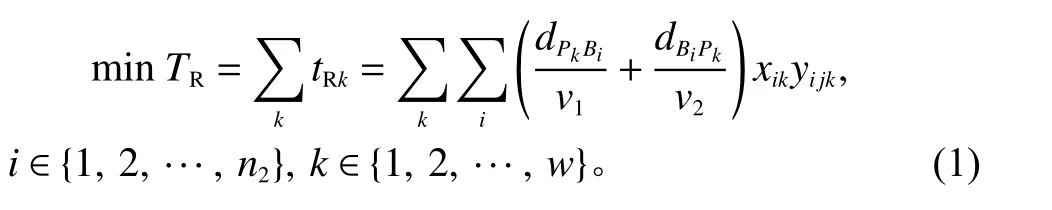
式(1)表示最小化出库作业时间，包括AGV从工作台到出库点的空载移动时间加上AGV从出库点至工作台的负载移动时间。

2) 单独入库作业。

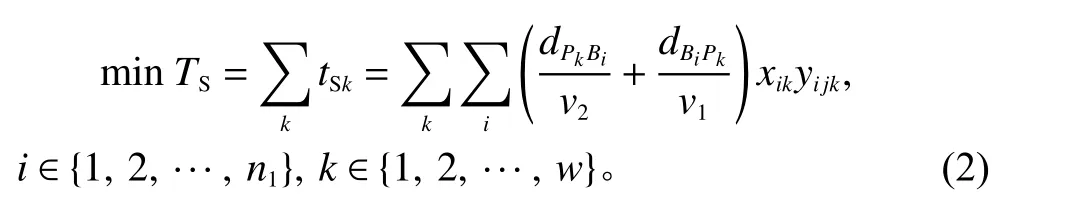
式(2)表示最小化入库作业时间，包括AGV从工作台到入库点的负载移动时间加上AGV从入库点到工作台的空载移动时间。

3) 联合出入库作业。

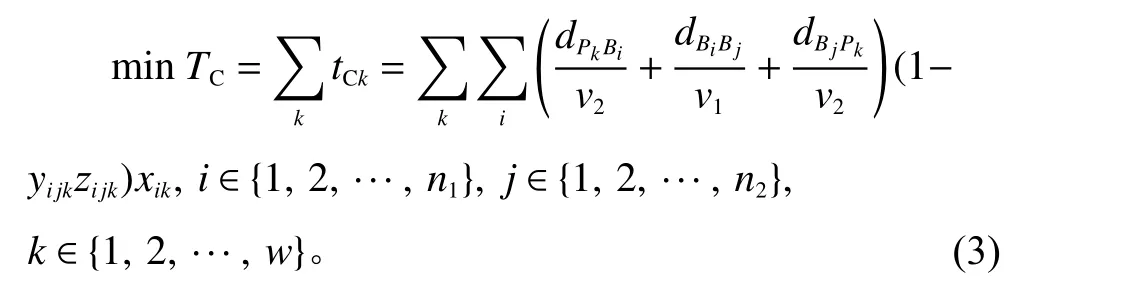
式(3)表示最小化联合作业时间，包括3部分：AGV从工作台到入库点的负载移动时间、AGV从任务i位置移动到任务j的空载移动时间、AGV从任务j移动至工作台负载移动时间。

4) 系统总作业时间。

由式(1)、(2)、(3)得多种作业模式并存下的总作业时间数学模型，优化目标为总作业时间最短。

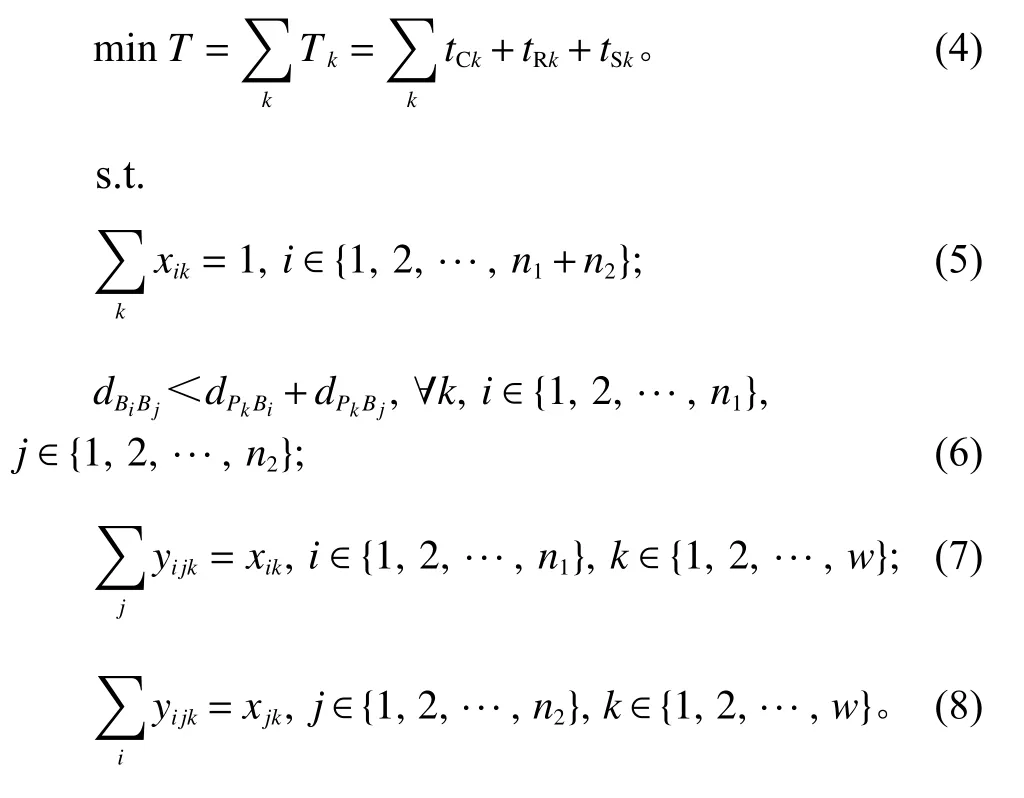
约束条件中，式(5)表示每个任务只能由一辆AGV执行；式(6)表示联合出入库任务AGV行走距离小于单独进行出入库作业AGV行走距离之和；式(7)、(8)表示单个AGV单次最多执行一个任务。

3 改进多种群遗传算法

与传统遗传算法(GA)相比，多种群遗传算法(multiple population GA, Multi-pop GA)[15]通过种群迭代提高解的多样性，搜索能力提高。本文在标准算法基础上，考虑了初始解判断规则和自适应遗传策略，以提高收敛速度。

3.1 编码方法

本算法采用实数编码形式，每个染色体中，基因数目表示任务总数，基因位置表示任务，基因数值为执行该任务的AGV编号。如图3所示，共10个任务，其中，任务1、4、8由1号AGV执行。

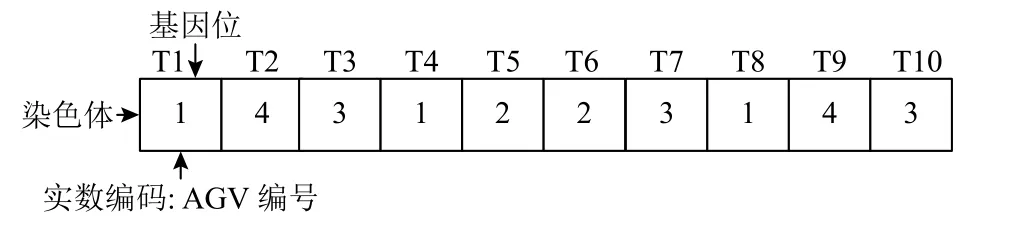
图3 编码设计Figure 3 Coding design

3.2 初始解生成及评价

为保证种群多样性，多种群遗传算法对不同群体采用不同算子，但如果初始解不能较好地分布在解空间，依然会使得不同种群趋向同一局部解。为解决此问题，本改进算法在初始解生成阶段加入判断过程。

已有初始解判断研究大多基于海明距离，但此方法多用于0-1编码规则，对实数编码适用性较差。图4编码中，两组基因的海明距离均为5，但放在执行环境中，基因组1中的顺序差异明显要小于基因组2的差异。

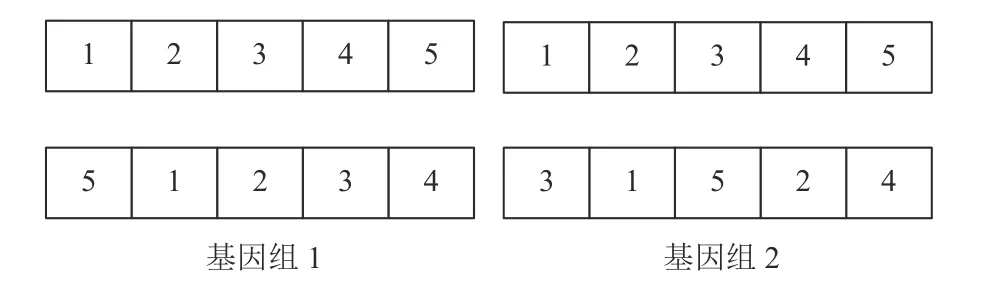
图4 基因组对比Figure 4 Genome comparison

为更好地描述初始解的距离，给出一种适用于实数编码的评价因子，该因子将基因位值缩放至十进制，即每个基因位的值为0～9。设每个初始解的基因位有m个，则最小值为 0,···,0 ， 最大为9,···,9。每次生成初始解，对实数差异大小进行判断，当差异大于10m×(1.25N)-1时，保留初始解，否则认定初始解差异性小，需重新生成。

3.3 自适应遗传算子设计

为有效控制种群进化方向，设计自适应遗传算子，主要考虑两个方面因素。

1) 所处进化阶段不同，对遗传操作的需求不同，在进化初期，可适当降低交叉和变异几率，以提高种群内部适应度值高的个体比例；在进化后期，种群内部个体差异性已较小，为避免陷入局部解，可提高交叉和变异的几率。

2) 为加快搜索，希望能尽量保持适应度高的个体即减少操作几率，能改变适应度低的个体即增加操作几率。

基于以上思路，给出了自适应遗传算子的计算式，交叉几率pci见式(9)，变异几率pmi见式(10)，其中，fi、favg、fmax分别为适应度第i代值、平均值及最大值。

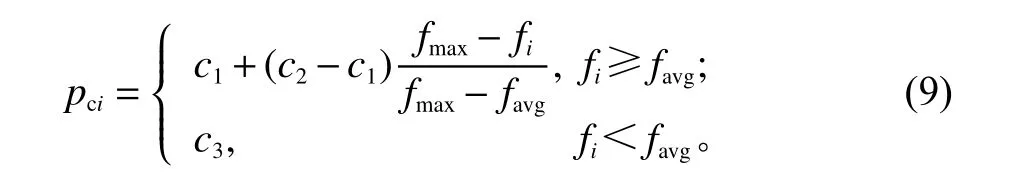
式(9)中，c1、c2分别为交叉基础概率的范围，c3为随机值，且1＞c3＞c2＞c1＞0。由计算式可知，当适应度值大于平均值时，可在规定的上下限内取值，且适应度值越高，交叉概率越小；当适应度值小于平均值时，交叉概率可高于基础概率的上限。

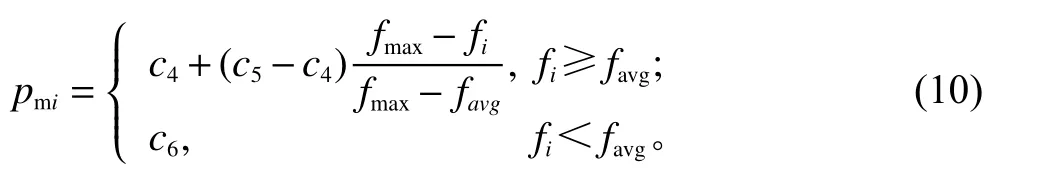
与式(9)类似，式(10)中c4、c5为变异基础概率范围，c6随机生成，且1 ＞c6＞c5＞c4＞0。

交叉操作中，对有m个基因位的个体，首先在(0, 1)区间产生两个随机数L1、L2，其次计算mL1、mL2并取整，得到交叉段起终点位置，最后对父代进行交叉得到子代，见图5。

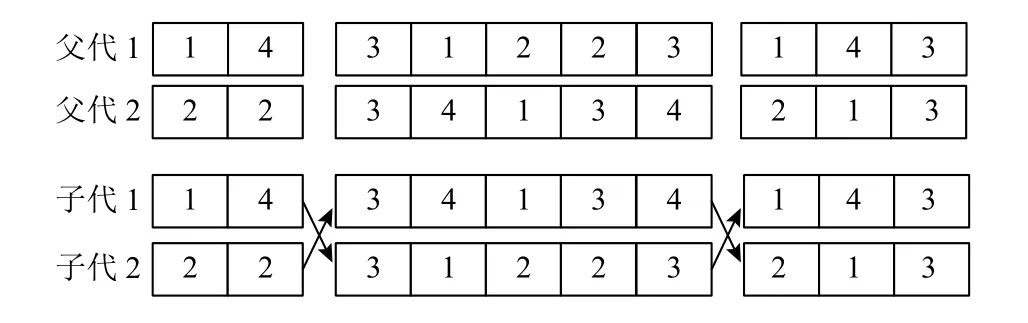
图5 交叉操作分析Figure 5 Example of cross operation

变异操作中，在1 ∼m中随机产生一个数，确定变异基因位，并将基因数值变异成其他随机编码。

多种群遗传算法中，既包含种群内部的进化，也包括种群间的交流，以保证协同进化，其中，个体迁移是衔接两者的关键。为避免频繁迁移，设定种群间最优个体每10代迁移1次。

3.4 适应度值与终止条件

式(4)目标为总作业时间最短，因此适应度函数f设为目标函数的倒数。将迭代次数作为终止条件，可以设置为1 000次。

4 算例分析及验证

4.1 算例初始条件

AutoStore为三维立体货架，考虑到AGV只在顶层移动，在某个货格或工作台顶部进行料箱的提取或存入工作时，和路径安排无关，因此，以货架顶层网格为路径地图。地图横纵分别有70个货格，每一个货格可用坐标节点来表示。设工作台数量为4个，分别布置在货架4个角，编号和坐标分别为A1(0, 0)、A2(0, 70)、A3(70, 0)、A4(70, 70)。AGV数量为5台，空载速度为1 m/s，负载速度为0.8 m/s。随机生成50个任务，其中出库27个，入库23个，对应出入库点的坐标见表1。

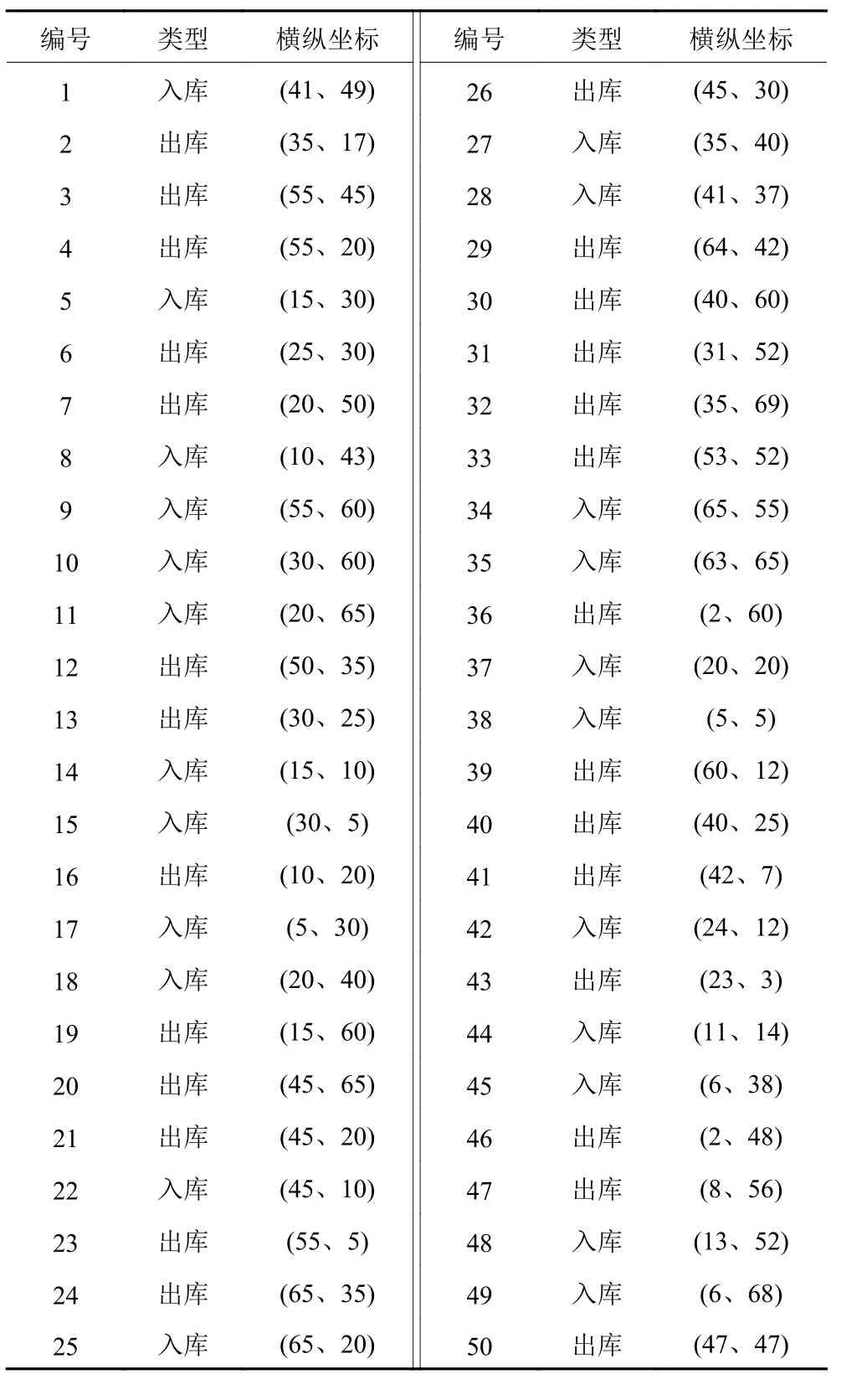
表1 出入库任务列表Table 1 Inventory task list

依次求解前20、前30和50个任务的AGV分配方案。算法设计时，取多种群算法的种群数为5，最大迭代次数为1 000。同时，为验证本文所提出算法(adaptive multi-pop GA)的有效性，分别与传统遗传算法(GA)、多种群遗传算法(multi-pop GA)进行对比。

4.2 任务规模为20的AGV分配方案

GA算法在第379次迭代得到最优解，Multi-pop GA算法在第360次得到最优解，本文所提Adaptive Multi-pop GA算法在第340次迭代达到最优，迭代过程见图6。

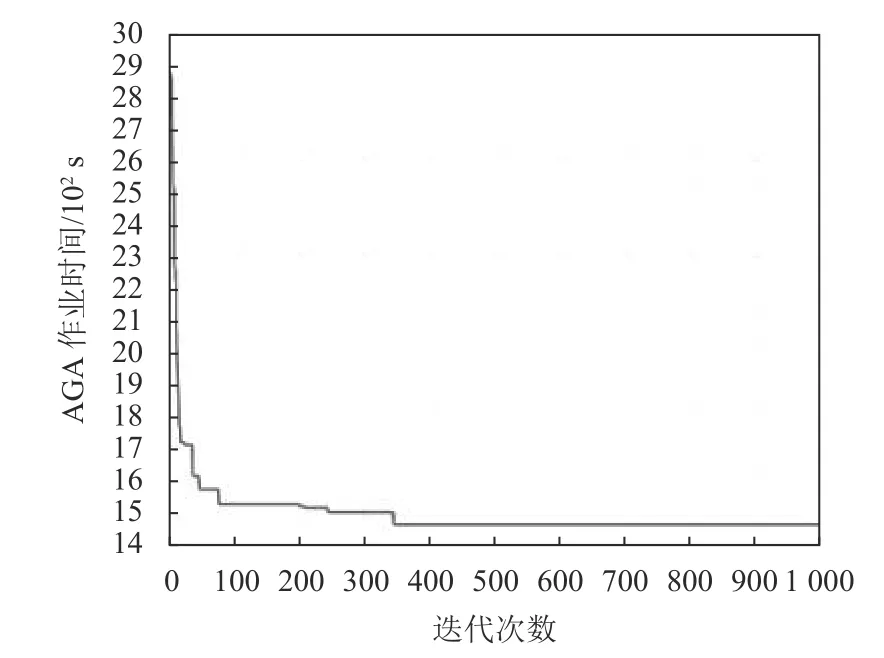
图6 Adaptive Multi-pop GA迭代过程(任务规模20)Figure 6 Calculation process of adaptive Multi-pop GA(20 tasks)

求解所得AGV调度方案见表2。对1号AGV，其行驶路径为从工作台A1出发，执行入库任务5，接着执行出库任务16，后回到A1，再依次执行入库任务14和出库任务6，最后回到工作台1。其余4台AGV调度方案详见表2。可以看出，1号、4号和5号AGV采用的是联合作业模式，2号AGV为联合作业模式与单独入库相结合，3号AGV为单独出库作业模式，3种作业模式并存，验证了本文所述模型的合理性。

表2 AGV分配方案(20个任务规模)Table 2 AGV scheme for 20 tasks

4.3 任务规模为30的AGV分配方案

经过验算，GA算法在第510次迭代得到最优解，Multi-pop GA算法在第460次迭代得到最优结果，而本文Adaptive Multi-pop GA算法在第450次迭代就得到最优结果，迭代曲线 (每一代的最短时间)见图7。

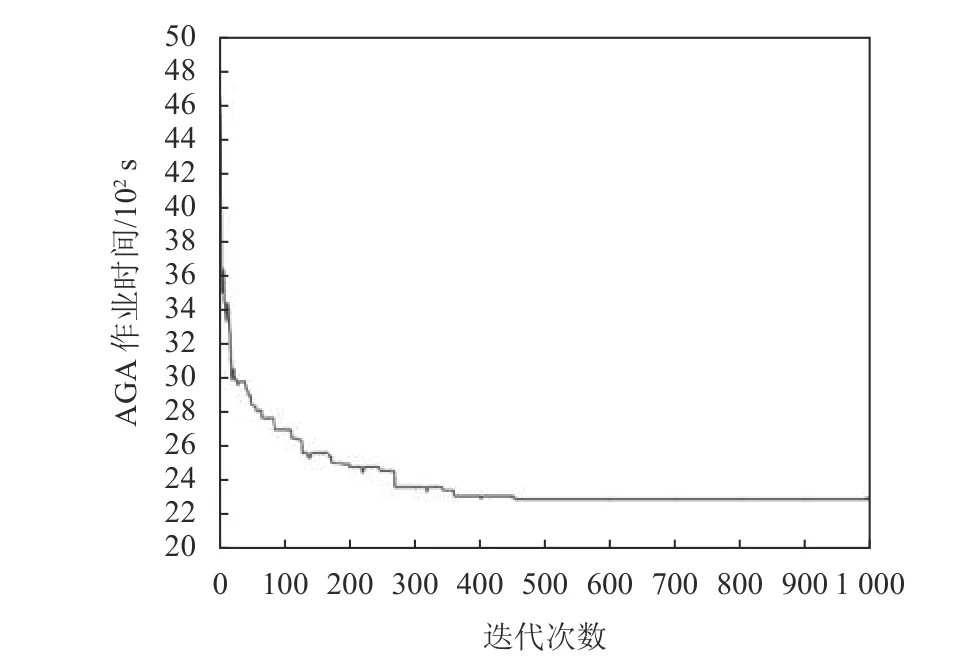
图7 Adaptive Multi-pop GA迭代过程(任务规模30)Figure 7 Calculation process of Adaptive Multi-pop GA(30 tasks)

求解所得AGV调度方案见表3。与20个任务规模类似，30个任务情况下也存在3种作业模式并存的情况。不同的是，随着任务规模增大，AGV活动范围更大，因此在任务结束后AGV往往会停在不同于起始工作台的位置。

表3 AGV分配方案(30个任务规模)Table 3 AGV scheme for 30 tasks

4.4 任务规模为50的AGV分配方案

GA算法在第900次迭代得到最优结果，Multipop GA算法在第750次迭代得到最优结果，而本文Adaptive Multi-pop GA算法在第720次迭代就得到最优结果，迭代过程 (每一代的最短时间) 如图8所示。

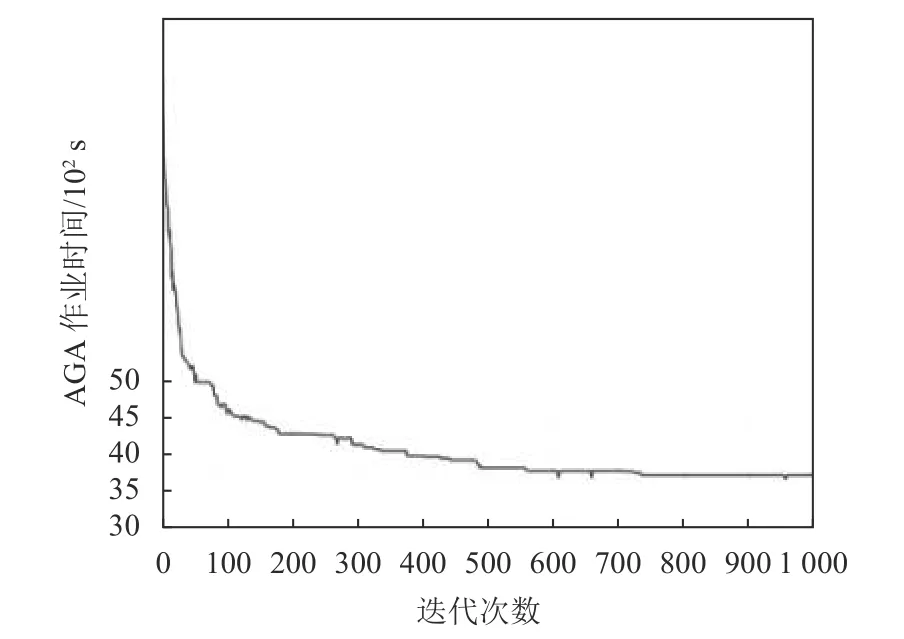
图8 Adaptive Multi-pop GA迭代过程(任务规模50)Figure 8 Calculation process of Adaptive Multi-pop GA (50 tasks)

求解结果如表4所示。随着任务规模进一步增大，对每台AGV，起终点不一致的情况增多，多种作业模式共存的情况下，路径更为复杂。

表4 50个任务规模下求解结果Table 4 Solution results under 50 tasks

4.5 不同任务规模求解对比

为验证算法的适用性，在相同环境下反复运算10次，取平均值。表5为模型求解结果对比，表6为搜索效率对比。

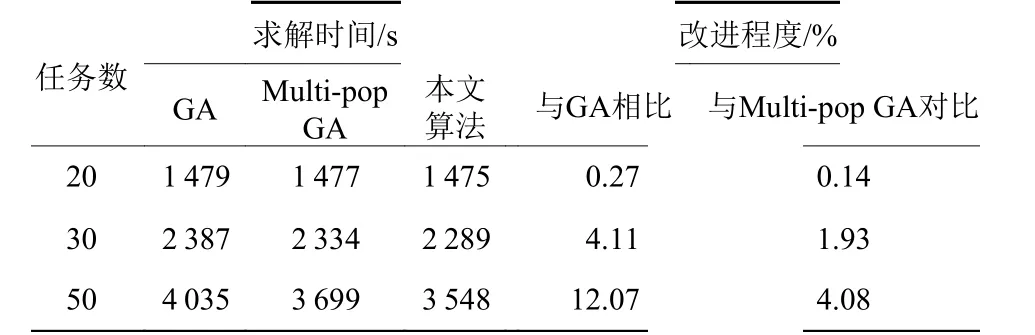
表5 不同算法求解作业时间对比Table 5 Comparison of different algorithms for solving job time

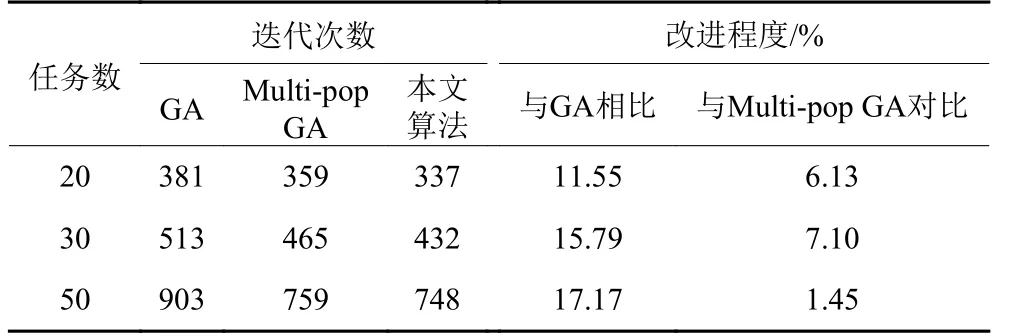
表6 不同算法搜索效率对比Table 6 Comparison of search efficiency of different algorithms

从求解结果分析，本文所提算法较传统GA和传统Multi-pop GA都有不同程度的提高，且随着任务规模的增加，搜索效果得到保证。从求解效率看，本文所提算法迭代速度更快，迭代次数更少。

5 结论

针对AutoStore仓储系统作业特点，研究了多AGV任务分配问题，主要结论如下。

1) 考虑到该系统出、入库单独作业和联合出入库作业共存的情况，给出了3种作业模式总时间最小模型，能反映该系统作业特点。求解算例表明，所得AGV分配方案中，3种作业模式并存，验证了模型的合理性。

2) 对传统多种群遗传算法从以下两方面进行改进：首先给出了适应于实数编码的初始解评价因子，增加初始解的均匀性；其次，给出了自适应遗传因子计算式，能根据进化程度和个体适应值情况确定不同的操作概率，以提高解的质量。不同规模算法计算表明，与传统遗传算法和传统多种群遗传算法相比，本文算法搜索效率和搜索效果都得到不同程度提高。

需注意的是，本文问题分析是在某一固定时间段内进行，在后续研究中，将进一步加入时间窗来满足订单处理的时效性限制。