基于VMD-MDE的柱塞泵磨损故障诊断研究*

2021-09-27曲全鹏曲海军

机电工程 2021年9期

曲全鹏,曲海军,张强

(1.河南工程学院工程训练中心,河南郑州 451191;2.河南理工大学机械与动力工程学院,河南焦作 454003;3.河南睿智液压设备有限公司,河南郑州 451191)

0 引言

柱塞泵在运行过程中发生故障时,会形成微弱的特征信号,并产生调制现象,从而淹没在背景噪声中。该现象显著提高了柱塞泵故障特征的提取难度,从而更难以获得其准确的模式识别效果[1-4]。

相对于小波分解与EMD分解过程,变分模态分解不需要设置大量调节参数,并且可以消除模态混叠和端点效应的问题,使信号被分解成包含多种中心频率的有效带宽,因此,该方法被广泛应用到了信号处理领域[5-8]。陈东宁[9]从VMD模态分量中选择了跟原始信号互相关系数达到0.3以上的IMF分量,实施了信号重构,通过测试发现,该方法能够对轴承故障进行精确诊断。刘岩[10]按照谱峭度差异重构了VMD分解形成的各分量,同时引入了MOMEDA算法,完成了对滚动轴承的故障诊断。

在采用相关系数选择法进行处理时,由于只获得了少数分量,此时在最初发生故障的过程中形成的故障信号强度非常低,无法对这些信号进行准确诊断,有些特征信号也被判断成噪声信号而被去除。因此,利用单一尺度DE已不能从柱塞泵复杂振动信号中准确分辨故障信息,此时首先需要对其信号实施多尺度分析[11-13]。

目前的研究多是通过变分模态分解特征能量重构法(VMD)来实现对故障的分析,但变分模态分解特征能量重构法在实际使用过程中,存在准确性不高的问题。

为了提高测试的准确性,本文设计一种通过变分模态分解特征能量重构法(VMD)和多尺度散布熵实现的柱塞泵滑靴磨损故障诊断方法,来分析在正常状态与不同位置时柱塞泵滑靴端面的磨损状态。

1 数学模型

1.1 VMD分解层数K确定方法

根据VMD算法简介可以发现,以该算法对信号进行处理需要先确定分解层数K。无论是EMD分析方法还是中心频率观察法,在进行分析时需要参考前期的经验,耗费大量时间,并且也不能保证其准确性。因此,可以选择能量变分模态分解(VMD)算法来实施分析,同时以能量收敛因子为判据,来完成对K值自适应分析,从而获得更快的处理速率,并提高其准确性[14-16]。

笔者将能量收敛因子表示成一定的形式,对原始信号先通过VMD分解获得能量余量,再跟原始信号能量进行比较[17]。

其中,能量收敛因子为相邻两分解层数能量比的差值,其表达式如下:

(1)

式中:f—原始信号;uk—第k(k=1,2,…,K)个模态函数;K—分解层数。

1.2 特征能量占比VMD重构(VMD)

为了发挥通过VMD方法获取的IMF信息的功能,防止因为只选中其中部分相关系数,或出现高峭度IMF参数二导致信号重构过程中的微弱故障信号去除问题,笔者设计了一种建立在特征能量占比(FER)基础上的信号重构方法[18]。

其具体计算步骤如下:

(1)假定VMD分解得到的K个IMF信号序列是x=(x1,x2,…,xK),之后计算得到各IMF的Fk。

将FER表示为Hilbert包络谱包含的前h倍频特征频率能量与总能量之比,将该比值作为判断特征信息的贡献度,即:

(2)

式中:Eh—第k个IMF的Hilbert包络谱特征频率在h倍频处对应的累积能量。

(2)统计每个FER的模态占比。

其表达式为:

(3)

(3)计算IMF归一化后的重构权重β。

即:

(4)

(4)计算重构信号。

即:

(5)

VMD多尺度散布熵故障诊断流程如图1所示。

图1 故障诊断基本流程图

2 信号收集以及分解、重构

2.1 信号收集

在柱塞泵保持正常运行状态,与滑靴端面达到0.1 mm、0.2 mm以及0.3 mm磨损程度时,笔者依次采集A10VS045型产生的的振动信号,控制采样频率为24 000 Hz,持续采样0.2 s,共采样4 800点,分别对各状态收集60组样本。

数据采集仪为MI-7016型。

信号采集方案如图2所示。

图2 柱塞泵磨损信号采集方案1—电动机;2—柱塞泵;3—加速度计;4—过滤器;5—压力表;6—溢流阀;7—油箱

将系统主油路压力设定在10 MPa,同时控制电机转速为1 500 r/min;共包含9个柱塞数,通过计算获得柱塞振动基频为225 Hz。

加速度传感器沿z方向产生的通道故障信号表现出最高峭度值[19],该结果说明柱塞在工作期间发生滑靴磨损引起斜盘冲击振动,是通过柱塞、滑靴以及缸体被传输到柱塞泵的端盖部位,这跟之前振动作用机制与故障信号传递路径一致,因此,可以分析该通道信号。

4种状态信号的时域变化情况如图3所示。

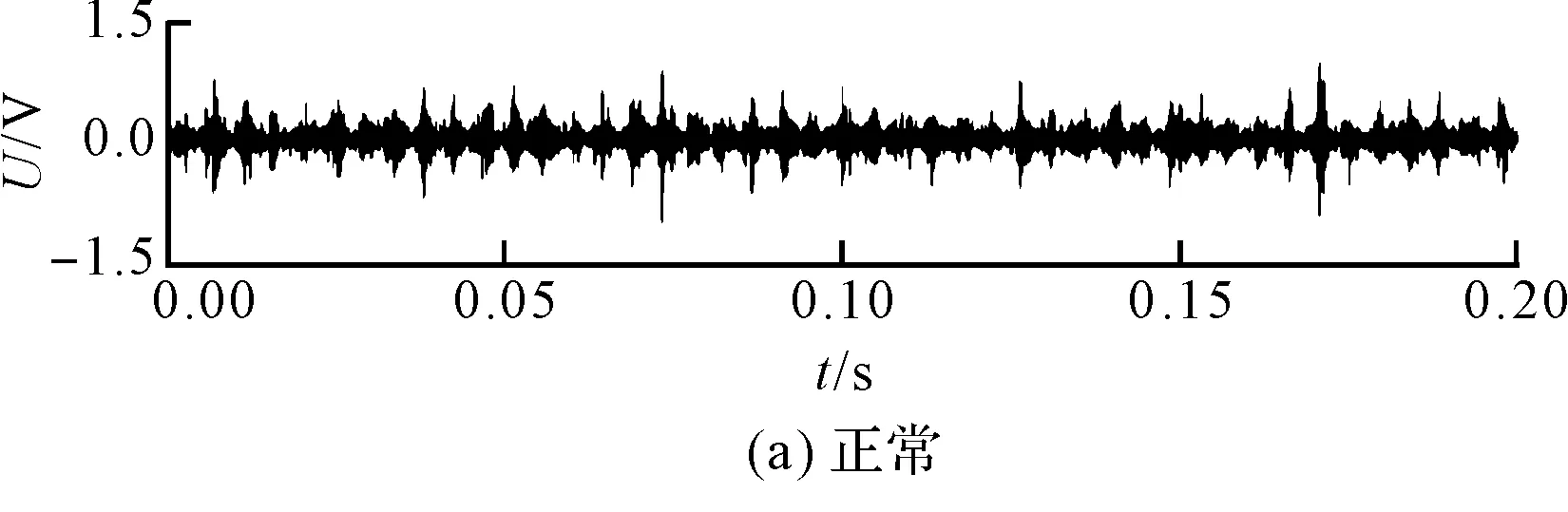
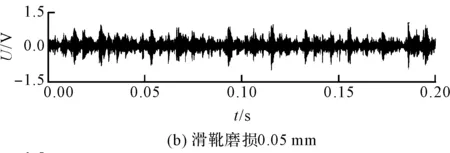
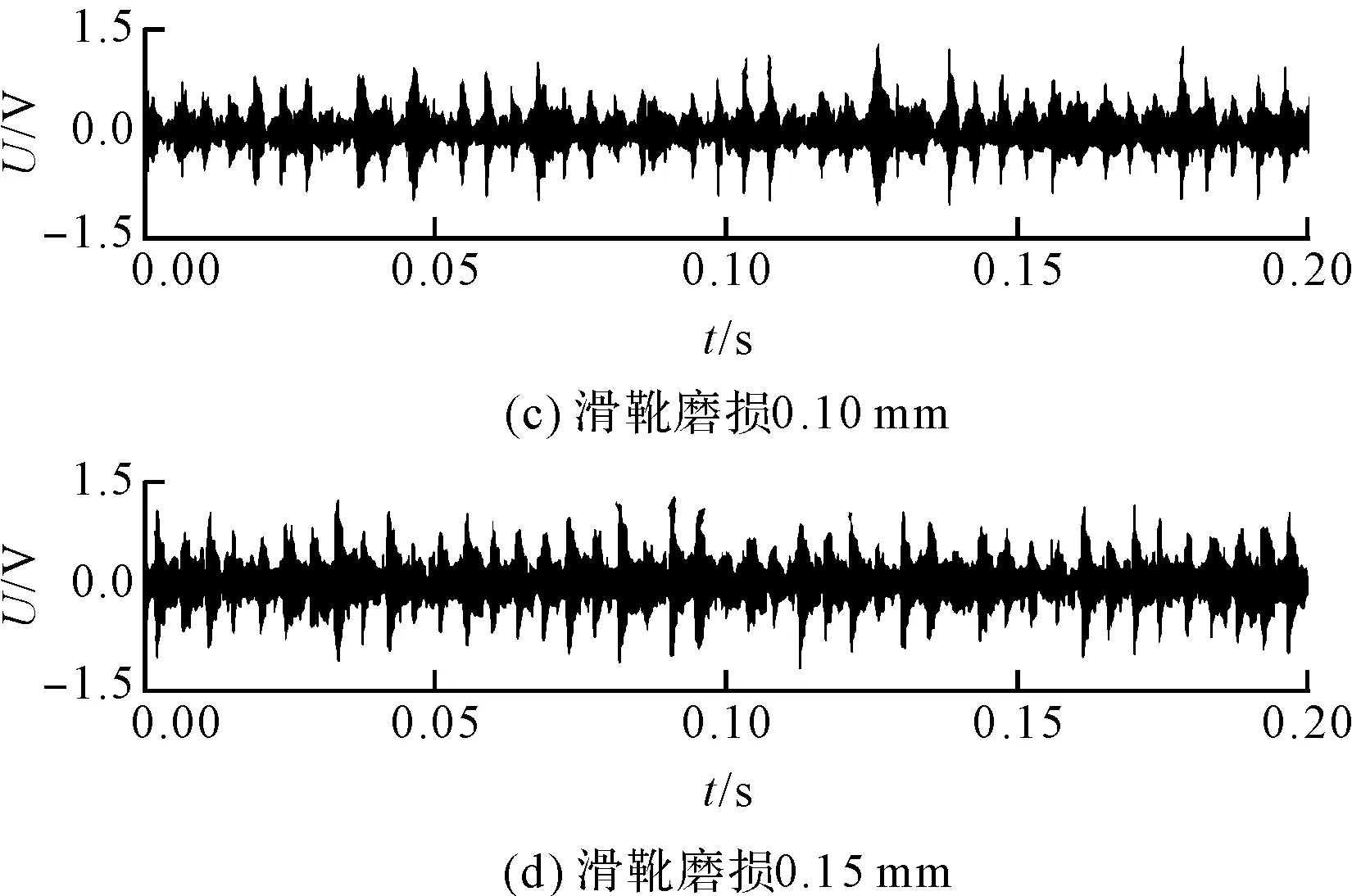
图3 4种状态信号时域图

图3中,信号具有典型的波动特性,可以作为基础信号进行后续研究;而且不能从时域图内准确分开4种状态,因此,需要对信号进行VMD分解和重构。

2.2 信号VMD分解和重构

针对各IMF分别计算特征能量占比Fk,柱塞与转轴振动基频分别为225 Hz与25 Hz,前者相对后者发生显著增大,因此,Eh按照上述特征频率的前8倍频累积能量进行计算。

接着计算IMF重构权重βk,同时计算归一化重构权重。

重构权重计算结果如表1所示。

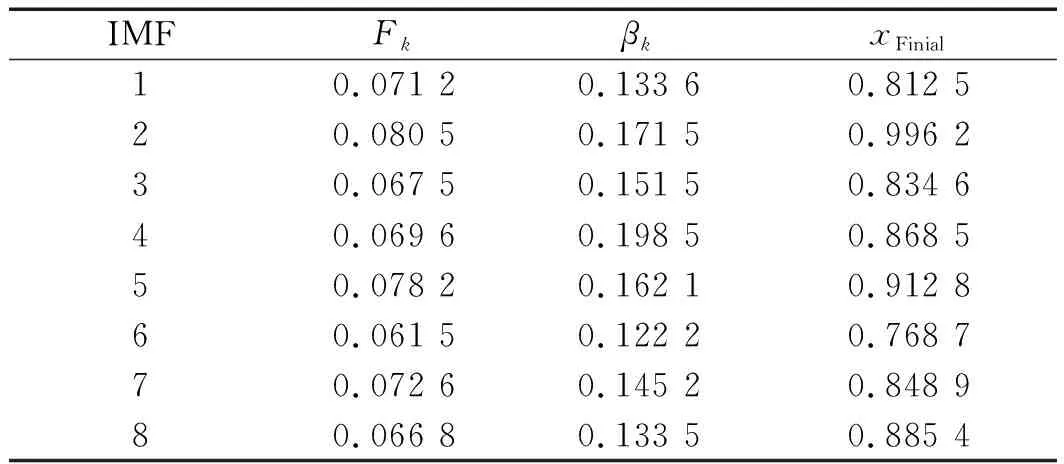
表1 重构权重计算结果

对表1中数据进行统计,得到以下重构信号:

xFinial=0.763 1x1+x2+0.867 2x3+0.831 4x4+0.947 3x5+0.702 1x6+0.823 6x7

(6)

式中:{xi,i=1,2,…,7}—IMF分量。

原始信号与VMD重构信号Hilbert包络图如图4所示。

图4 原始信号与VMD重构信号Hilbert包络图

图4中,与原始信号进行比较可知,VMD重构信号中高频噪音成分发生了明显降低,因此,可以通过VMD将噪音高频分量有效剔除。

3 结果分析

3.1 特征提取结果分析

笔者对各状态下的多尺度散布熵变化规律进行分析,同时提取得到有效尺度散布熵,并将其作为故障特征向量。

笔者以滑靴磨损为0.05 mm的条件作为研究对象,以尺度因子scale=10,测试了4个状态下的不同时间尺度MDE值。

4种状态MDE值结果如图5所示。

图5 4种状态MDE值

图5中,与正常MDE相比,不同程度的滑靴磨损后，其振动信号MDE均表现出明显的降低变化,表明该方法对处理振动信号是有效的;逐渐增加时间尺度之后,可以促进粗粒化序列发生随机性的降低,并减小复杂度,这使得4种状态下MDE都出现了减小的结果,同时获得了更小的差异;正常信号到第2时间尺度时出现了MDE的峰值,在其余各状态下都是第1时间尺度。

VMD重构信号峰值多尺度散布熵结果如图6所示。