航空燃油齿轮泵流动机理的数值模拟研究*

唐 庆,单金光,周 龙,周振华,万 方

(1.中国航发贵州红林航空动力控制科技有限公司,贵州 贵阳 550009;2.空军装备部 驻贵阳地区第二军事代表室,贵州 贵阳 550009)

0 引 言

齿轮泵是航空发动机燃油传动系统中比较常用的液压正排量装置[1-3],用于输送燃油或给燃油增压[4]。齿轮泵通常由泵体、前后盖和一对相互啮合的齿轮组成,在齿轮脱开侧和啮合侧各形成了两个封闭空间,分别称为吸油腔和排油腔。当齿轮转动时,吸油腔的空间的体积变大,将液体吸入;排油腔的空间的体积变小,将液体从齿轮外侧挤入管路中去[5-7]。齿轮泵结构简单、造价低廉、重量轻、工作要求低,应用十分广泛[8-11]。

齿轮泵的性能表现受到内部流态的影响,因此,对齿轮泵内部流动的机理进行研究,可为其在实际工程中的应用提供理论支撑。

齿轮泵内的流动属于复杂的三维非定常粘性流动,理论分析和实验研究难以实现对流场机理的深入详细分析。

数值模拟方法可以在较少的人力物力成本下,得到细致的流场模拟数据。因此,基于数值模拟的齿轮泵内流特性研究近年来得到很大的发展。聂瑞等[12]基于Fluent中对齿轮泵内部的压力分布进行了数值求解,与理论计算结果进行了对比,发现结果基本吻合。吕程辉等[13]应用动网格技术,对内啮合齿轮泵内部的非定常流动细节进行了数值模拟,得到了不同工况下的流动特性和性能表现,分析了其变化规律。吴晓等[14，15]通过动态数值模拟研究了外啮合齿轮泵的内流特性机理,得到了速度和压力等物理量的分布,研究了工质的流动状态和齿轮泵结构受到的载荷。段志善等[16]应用Fluent软件,通过二维流场的数值模拟,分析了工况变化对工作介质流态和泵的工作性能的影响。

目前,国内外对齿轮泵内流已开展了广泛的研究,但多数研究没有考虑齿轮泵转速对内部流场的影响。

本研究建立简化的齿轮泵二维几何模型,生成非结构网格,并设置合理的边界条件;在Fluent中采用k-ε湍流模型和动网格技术,对不同转速下的齿轮泵内流场进行数值计算,得到压力云图和速度矢量图等结果;通过计算结果的对比分析,研究流场分布特征和转速对流动的影响,为齿轮泵的运行维护和优化设计提供理论依据。

1 齿轮泵模型

1.1 几何模型

本文研究对象为某航空发动机所采用的外啮合燃油齿轮泵,理论上齿轮泵内部流场为三维流动,但三维问题求解需要较大的计算量。考虑到齿轮泵的几何形状具有对称性,流动参数沿着齿轮轴方向近似保持不变,在工程中可以近似视为二维流动,因此,此处把齿轮泵几何模型简化为二维模型。

笔者采用的几何模型由泵壳和两个齿轮构成,如图1所示。

图1 几何模型

在图1中,两个齿轮啮合处上侧空间为吸油腔,下侧空间为排油腔,上方边界为燃油入口,下方边界为燃油出口;左、右两侧齿轮旋转方向分别为逆时针和顺时针,将燃油从入口吸入吸油腔,传送至排油腔,并从出口排出。

1.2 网格与边界条件

在齿轮泵内流场计算中,泵体内的工作空间会随着齿轮的转动发生不断的变化,需要采用动网格技术来实现网格的不断变形重构。动网格技术主要用于模拟边界运动导致流场区域随时间改变的问题[17,18]。其中,实现网格随边界运动而变形的方法有滑移网格法、重叠网格法、弹性体方法、弹簧变形法和局部网格重构法等。

弹簧变形法的基本思想是把网格类比于弹簧系统,即假设网格节点之间的连线由线性弹簧代替,根据胡克定律计算出两个网格节点之间的力;变形前的网格等价于处于平衡状态的弹簧系统,各个网格点受到弹簧力的作用,并处于受力平衡状态,当边界上的网格点发生位移,网格点之间的弹力发生改变,系统不再处于平衡状态,此时,为了恢复平衡状态,需要改变内部各个节点的位置,根据胡克定律和平衡方程,可以计算出系统新的平衡状态下各个网格点的坐标,把新的平衡状态下的各个节点及弹簧作为变形后的网格。

弹簧变形法的优点是不会对网格拓扑造成改变,在某些情况下可以减少一定的数值误差。但是,在弹簧变形原理中,当边界运动的尺度大于网格尺度,会出现网格质量下降、畸变过大、负体积等问题,导致计算发散或误差较大。

局部网格重构技术则是针对上述问题的一种解决措施,其基本原理为:通过网格畸变率和网格尺寸等指标,识别出网格质量较差的网格,然后对这部分网格进行局部重新生成,从而得到满足要求的网格。

在航空燃油齿轮泵转动过程的流场模拟中,笔者同时采用弹簧变形法和局部网格重构技术,当弹簧变形原理的网格质量降低到一定程度时,通过局部网格重构来提高网格质量。

在Fluent中使用动网格模型解决问题的第一步为定义初始网格,第二步为指定运动规律和边界运动模式,指定运动规律的方式包括边界型函数和用户自定义函数(user defined functions,UDF)。

本文中的初始计算网格采用三角形非结构化网格,如图2所示。

图2 网格示意图

在齿轮啮合处的局部网格如图3所示。

图3中,采用UDF把齿轮边界的运动方式定义为绕齿轮轴的定轴转动。在每个迭代步中,通过弹簧变形法和局部网格重构法实现网格变形,网格伴随着齿轮的转动啮合过程不断重构。在齿轮啮合处,齿轮间留有缝隙,对此处的网格进行加密,保证运动过程中网格不出现负体积。

齿轮泵内流场边界条件设置如下:齿轮泵入口设置为压力入口边界条件,入口压强5 000 Pa;齿轮泵出口设置为压力出口边界条件,出口压强2 MPa;齿轮表面设置为移动无滑移壁面;其他壁面为静止无滑移壁面。

2 控制方程与计算方法

本文所研究齿轮泵的工作介质为航空燃油,其具体参数如表1所示。

表1 油介质物理参数

离心泵内部流动为非定常、不可压缩粘性湍流流动。湍流是由于流体运动方程的非线性而产生的一种不规则的流动状态,实际工程中大部分流动都是湍流。目前,对湍流进行求解的思路有:直接数值模拟、大涡模拟和雷诺平均法。

直接数值模拟是指直接对原始的NS方程进行数值离散求解,其优点是可以获得较多的湍流脉动细节,缺点是对网格密度和计算量的要求极高,在实际工程中尚难以应用。

大涡模拟则是把湍流运动中大尺度的涡结构进行直接求解,小尺度的涡结构通过模型进行模化。大涡模拟的计算量少于直接数值模拟,但仍可以保留一定量的湍流细节,目前在工程中的应用刚刚起步。

而雷诺平均法是指把湍流运动拆分为平均运动和脉动,建立平均运动的方程,而脉动量对平均量的影响通过模型表示。雷诺平均法计算量较小,而且工程实际中往往更关心平均流动,因此雷诺平均法目前得到了广泛的应用。

综合考虑计算量和研究需求,本研究采用雷诺平均法。雷诺平均法采用雷诺平均方程作为控制方程,连续性方程和动量方程分别为[19]:

如今，已有一大批绿色建材家居企业落户荆门，因为荆门拥有发展秸秆板材的资源、产业、平台和政策等多方面优势，具有做大做强绿色建材家居产业的先决条件。

(1)

(2)

式中:ρ—密度;u—速度;p—压力;μ—黏性系数。

雷诺平均方程中包含脉动速度的项称为雷诺应力项,由于雷诺应力项的存在,模型不满足封闭性,需要湍流模型对雷诺应力进行模化求解。

工程中常用的湍流模型多以Boussinesp假设[20]为基础,即:

(3)

式中:μt—涡黏性系数。

μt不反映材料的物理属性,而是反映湍流特性,并且与实际的流场有关。

基于Boussinesp假设的湍流模型又称作涡黏模型。涡黏模型中包含不同的类型,根据方程的数量可以分为:零方程模型、一方程模型和两方程模型。其中,零方程模型使用代数方程对时均速度和涡黏系数建立关系式,一方程模型和两方程模型均通过微分方程对时均速度和涡黏系数建立关系式。

目前,零方程模型只在简单流动的模拟中效果较好,对复杂流动的模拟效果较差,在工程实际中很少使用。一方程模型以SA模型为代表,在航空领域的CFD计算中得到广泛应用;但其对空间尺度变化较大的问题计算误差较大。两方程模型中的k-ε模型具有适用范围广泛和计算量适中等优点,在工程实际中得到了较多的应用。

(4)

(5)

(6)

(7)

(8)

(9)

式中:υ—运动黏度;Gk—湍动能源项。

其他相关参数的取值为C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0，σε=1.3。

在Fluent中对模型进行求解,由于燃油可视为不可压缩流体,笔者选择压力基隐式求解器。空间离散格式设为一阶迎风格式,时间离散格式设为一阶隐式格式,笔者选择SIMPLE算法进行迭代计算,时间步长为5×10-6s。齿轮转速取1 000 r/min、2 000 r/min和3 000 r/min 3种工况。

3 计算结果分析

在出口和入口压力保持不变的情况下,笔者改变齿轮的转速,分别对转速为1 000 r/min、2 000 r/min和3 000 r/min 3种工况进行计算,得到齿轮泵内的压力分布和速度矢量的分布;笔者对结果作进一步分析,研究流场结构以及转速对流场的影响规律。

不同转速下齿轮泵内部静压分布如图4所示。

(a)1 000 r/min

由图4可知:在齿轮泵中,齿轮进入啮合的区域为局部高压区,而齿轮退出啮合的区域为局部低压区;随着转速提高,低压区压力进一步降低、高压区压力则进一步升高,而其他区域压力变化不明显。

齿轮啮合区附近静压分布局的部放大图如图5所示。

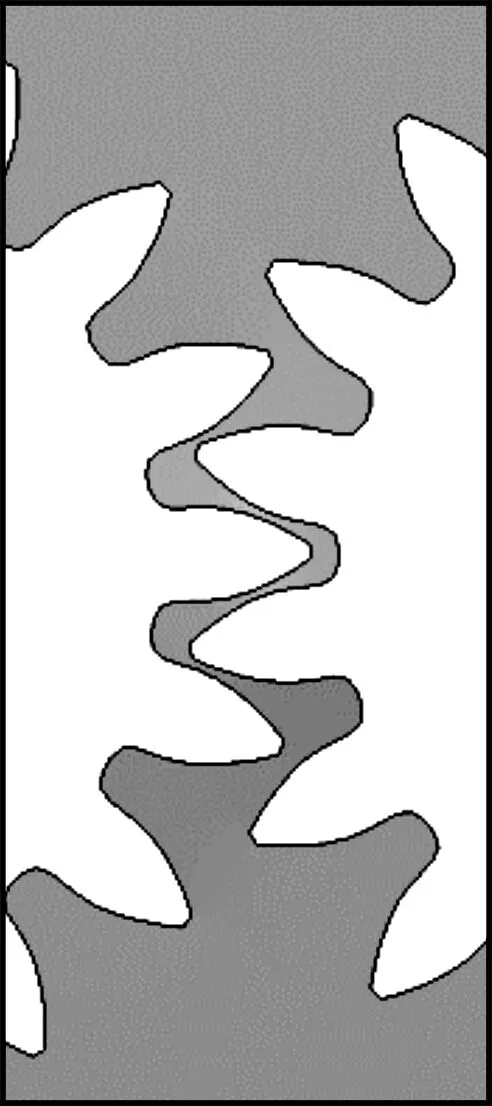
(a)1 000 r/min

通过图5可以进一步看出:随着转速提高,齿轮泵啮合区附近的最高压力和最低压力的差值逐渐增大。

齿轮泵中最高压力和最低压力随转速的变化曲线如图6所示。

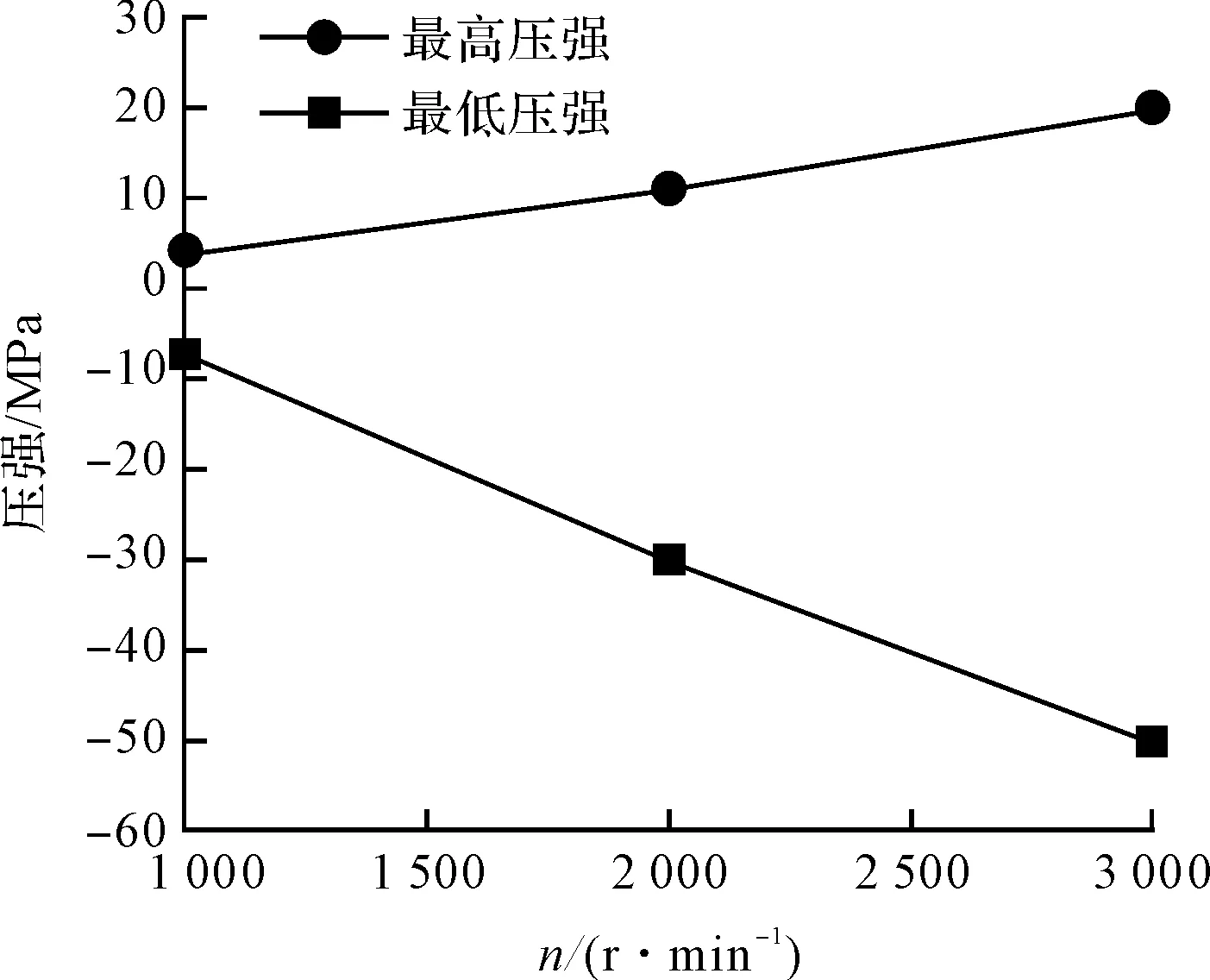
图6 齿轮泵中最高压力和最低压力随转速的变化

通过图6可知:随着转速的提高,最高压力和最低压力值近似以线性规律增大和减小,两条曲线的差值逐渐增大。这说明齿轮表面承受的应力波动深度逐渐变大,疲劳损伤的可能性增大;同时,由于最低压强数值变小,气蚀发生的可能性也更大。因此,在实际工程中应合理设置齿轮泵转速,以避免疲劳损伤和气蚀的产生。

泵内流场的速度矢量分布如图7所示。

(a)1 000 r/min

由图7可知:在齿轮泵的齿槽处,流体随齿轮一同运动,且流速比泵壳壁面附近略大;在轮齿啮合处,由于流道较窄,流体流速达到最大值。随着转速的提高,齿槽处的流体速度略有增大,齿轮啮合处的速度明显增大(齿轮转速分别为1 000 r/min、2 000 r/min和3 000 r/min的工况下,啮合区的流速最大值分别约为105 m/s,226 m/s和269 m/s);

同时可以看出,随着转速的提高,出入口的速度大小略有增加,因此,齿轮泵的流量也会随转速提高而增大。

轮齿泵啮合区附近的速度矢量图如图8所示。

(a)1 000 r/min

由图8可知:齿槽中的流体随齿轮运动,在啮合区正上方的吸油区中,由于齿轮脱离啮合,该侧空间体积增大而将流体吸入,流体速度方向指向啮合区;

在啮合区正下方的压油区中,由于齿轮进入啮合,该侧空间体积减小而将流体排开,流体速度方向背离啮合区。

4 结束语

本研究基于雷诺平均方程、k-ε湍流模型和动网格技术,在不同转速下对齿轮泵内流场特性进行了数值模拟,对比分析了流场的分布规律和转速对流动的影响。

通过研究得到以下结论:

(1)齿轮旋转过程中,齿轮进入啮合的区域形成局部高压区,退出啮合的区域形成局部低压区。最高和最低压强的差值随转速提高近似线性增大,增加了气蚀和疲劳损伤的可能性,因此在实际工程中需要合理控制齿轮转速;

(2)在齿槽处,流体速度矢量方向与齿轮转动方向一致;在吸油区中,速度矢量方向指向齿轮啮合区;在压油区中,速度矢量方背离齿轮啮合区。在齿轮啮合处,油介质的流动速度达到局部最大值,且最大流速值与齿轮转速正相关。

此外需要指出的是,在目前的研究中,笔者所选取的工况种类和数量相对较少,因此,在接下来的研究中,笔者还将就更多不同工况下齿轮泵的流动特性作进一步的研究。