基于ABAQUS的模块化机械手动静态分析及结构优化
2021-09-27王文军李福送林伟健
王文军,李福送,林伟健
基于ABAQUS的模块化机械手动静态分析及结构优化
王文军,李福送,林伟健
(柳州工学院 机械工程学院,广西 柳州 545000)
模块化机械手在焊接过程中,运动到某些位置时出现振动幅度比较大的现象,影响了焊接的精度和质量。对模块化机械手进行动静态分析,首先利用三维软件UG NX 12.0对模块化机械手进行建模,再利用有限元分析软件ABAQUS对模块化机械手进行静力学分析和模态分析。静力学分析结果表明:模块化机械手结构的刚度和强度达到工作性能要求。动力学分析结果表明:模块化机械手第1阶固有频率(1=30.870 Hz)和减速器输入最小的转频(29.13 r/min)很接近,容易出现共振现象。在对第6轴结构优化后进行验证分析,得出第1阶固有频率为36.033 Hz,比原来提高了16.72%,远离了减速器的输入转频,避免了共振。本研究为对模块化机械手改进提供了理论依据。
模块化机械手;ABAQUS;固有频率;共振;结构优化
工业机器人是一种能自动控制并可重复编程的多功能操作机,在改进生产模式、优化工作环境、提高产品质量、降低运营成本等方面赢得了企业的广泛关注,目前广泛应用于搬运、装配、焊接、涂装等领域[1]。工业机器人的种类和样式繁多,模块化机械手是其中之一,优点是方便安装与拆卸、价格相对较便宜。模块化机械手在焊接过程中,有时会出现剧烈振动现象,影响焊接精度和质量,且噪声较大。
目前,已有学者对工业机器人的动静态特性进行研究,胡义华[2]利用ANSYS软件对物流货物抓取机械手关键构件的结构进行模态分析,得出构件具有良好的动力学性能。陈彦宇等[3]利用ABAQUS软件对桁架机械手进行静力学分析和模态分析,得出机身最大变形量和整机的最低固有频率低于激振频率,不会发生共振。崔书婉等[4]利用ANSYS软件对焊接机器人进行静应力分析和模态分析,根据实际情况提出对应优化方案,发现优化后的焊接机器人在提高了强度、刚度的同时实现了轻量化。赵军等[5]利用UG软件系统CAE分析模块建立在最大垂向力工况下驱动桥壳的动静态性能分析模型,得出降低桥壳厚度可以提高其低阶固有频率,从而提高桥壳刚度。
对模块化机械手进行动静特性分析及结构优化,实现焊接精度和质量的提高,对模块化机械手的应用有着现实意义。本文以模块化机械手为研究对象,以现场原型为基础,从理论方面进行研究。利用UG NX 12.0软件对模块化机械手进行三维建模,再利用ABAQUS软件进行动静态特性分析,找出大幅度抖动的原因并进行结构优化和改进,从而达到消除或抑制大幅度抖动的目的。
1 模块化机械手静力学分析
模块化机械手属于关节型机器人,有第1轴~第6轴共6个关节,如图1所示。在第6轴末端法兰处安装焊枪。用地脚螺栓固定底座。首先对模块化机械手进行静力学分析,求出机械手主体结构在极限位置时各轴的应力值和最大变形量。确保模块化机械手不因自重原因出现强度和刚度不能满足工作性质要求的情况。
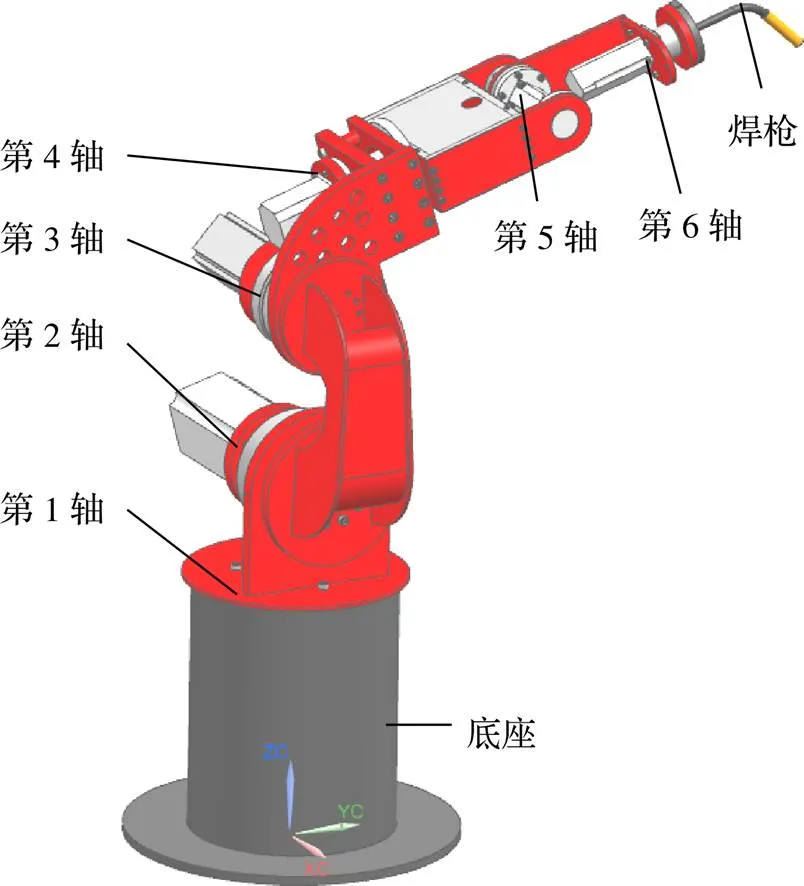
图1 模块化机械手三维模型
1.1 三维建模
根据模块化机械手的技术资料和现场实物,利用UG NX 12.0对其进行建模。
由于模块化机械手零部件较多,结构较复杂。在确保符合工程技术要求的前提下,对模块化机械手的三维模型进行相应简化,使有限元分析模型在计算机得到高效运算。
简化原则如下[6-7]:
(1)对一些复杂的零件,在保证主体结构性能的提前下进行简化,例如删除倒角,小孔;
(2)删除螺栓和螺母连接,在ABAQUS相互作用模块中对连接部件设定连接方式;
(3)对电机、编码器、焊枪、电线进行简化或在对应连接部件上进行质量附加。
UG NX 12.0和ABAQUS可实现无缝对接。模块化机械手三维模型可直接导入ABAQUS。导入后对模型进行相应检查,确保模型完整性。
本台模块化机械手应用于焊接,焊枪重量相对比较轻,所以模块化机械手的各轴连杆构件主要是承受各轴部件自身重力而引起的应力和应变。极限位置是指模块化机械手受到最大应力、应变和变形量的位置,也就是各轴部件的重力离底座最远的位置。在极限位置,末端执行器处(焊枪处)是变形量最大的位置[8]。本文选择模块化机械手在焊接的极限位置进行分析,如图2所示。
1.2 定义模型材料属性
模块化机械手底座、第2轴和第3轴的部件材料主要是Q235;第4~6轴的部件材料主要是铝合金ZL108。首先要对模块化机械手各部件进行材料属性设置,如表1所示。
在ABAQUS的属性模块中输入各种材料参数时,要统一单位制,因为ABAQUS不会对单位进行分辨[9]。
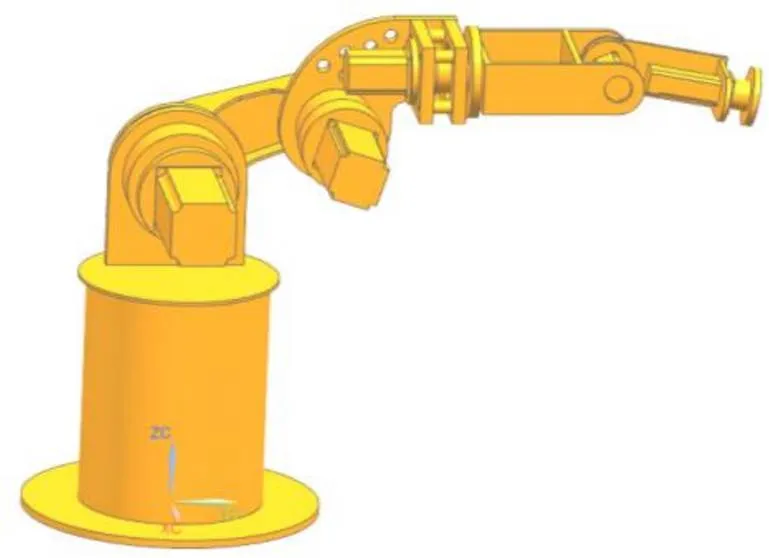
图2 模块化机械手的极限位置

表1 模块化机械手材料参数表
1.3 相互作用
模块化机械手各轴之间是通过电动机和减速器进行连接的。在静止状态下,各轴之间的连接相当于刚性连接。在相互作用的模块中设置为绑定约束[9]。
1.4 添加载荷和约束
模块化机械手和地面的连接通过地脚螺栓进行固定,在设置约束时对底座下端进行完全固定。在模块化机械手末端法兰处施加焊枪自重(≈1 kg)。模块化机械手其他各轴只受到自身重力的作用,没有受到其他外部载荷,不需要施加载荷。
1.5 网格划分
因模块化机械手零部件较多,有的较复杂,所以在ABAQUS中采用“四面体”网格划分[9]。
1.6 求解结果
从图3可看出,模块化机械手极限位置姿态应变最大发生在第2轴和第3轴的连接部件(大臂)。

图3 积分点应变云图
从图5可看出,最大的变形量是在第6轴末端法兰处,值为0.17 mm。和前文分析末端执行器处(焊枪处)是变形量最大的位置相吻合。本台模块化机械手是用于焊接,由于自重而出现的最大变形量符合工程要求。
综合上述分析可得出:模块化机械手静力学分析结果符合工作性质要求,不需要增加强度和刚度。

图4 弹性应力云图

图5 空间位移云图
2 模块化机械手模态分析
焊接过程中,模块化机械手在某些位置出现大幅度抖动现象。要找出大幅度抖动的原因,就要对模块化机械手进行动力学分析。现利用ABAQUS对模块化机械手进行模态分析,求出其固有频率和相应振型。
2.1 理论基础
模态分析的任务是求出结构系统各阶模态参数,譬如系统的固有频率和振型、模态质量、模态刚度、模态阻尼等。由弹性力学可以得到结构系统的有限元方程为:

在进行模态分析时,假设结构是不受外力作用的自由振动系统,则自由振动方程为:
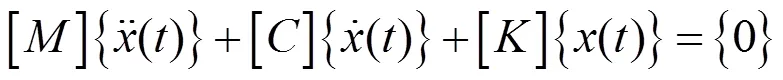
由于阻尼对结构的固有频率的振型影响不大,所以可以忽略阻尼的影响,则无阻尼自由振动方程为:
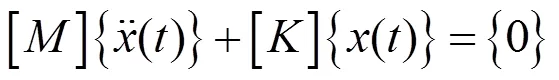
假设结构作简谐振动,则式(3)的解可以设为:

现代市场营销模式把消费者的利益和需求放在首要位置,这是市场营销的一场巨大变革。很多企业在企划市场营销之前,都要对消费者的消费需求和消费欲望与市场行情进行客观、详细的深入了解。其次,企业要针对自身的产品对行业内部的市场饱和程度进行调研,准确针对自身的产品进行市场定位,结合企业自身的情况和未来发展的方向,对潜在的消费者、市场、客户进行精准的定位。在完成这一系列的前期转化工作之后,企业集中所有的人力、物力、财力制定出准确的市场营销计划和方案,很好地落实到实践中去,实现社会、消费者和企业三方共赢的良好发展趋势。
结合式(3)和式(4),可得:

求解式(4)、式(5)就可以得出结构的固有频率和相应的振型[10-11]。
2.2 模态分析
由于模块化机械手的结构姿态是随着各轴转动而发生改变的,所以其在各种姿态下的固有频率和相应振型会有所差异[11-12]。为了得到与本文研究有关的数据,在现场记录模块化机械手出现大幅度抖动现象的各种姿态。本文选择具有代表性的姿态进行模态分析。
结合现场分析,模块化机械手的动力主要由6个轴的伺服电动机通过减速器提供。模块化机械手在焊接过程中,移动速度比较缓慢,现场外部激励输入频率也相应较低,所以只需研究模块化机械手的低阶模态。本文分析模块化机械手前8阶的固有频率和相应振型。
在ABAQUS中对模块化机械手进行模态分析时,前面的操作步骤和静力学分析的操作步骤基本一致,主要区别是模态分析的“分析步”需选择“线性摄动分析步”→“频率”,设置相关参数[9]。模态分析结果如图6、图7所示,其前8阶固有频率归纳如表2所示。
从表2可以看出,模块化机械手的前8阶固有频率为30.870~260.06 Hz,每阶固有频率值之间比较接近,特别是前3阶。
从图6、图7可以看出,模块化机械手前8阶的振型主要表现在第4轴、第5轴和第6轴上。计算出的固有频率和相应振型为下一步结构优化提供了依据。
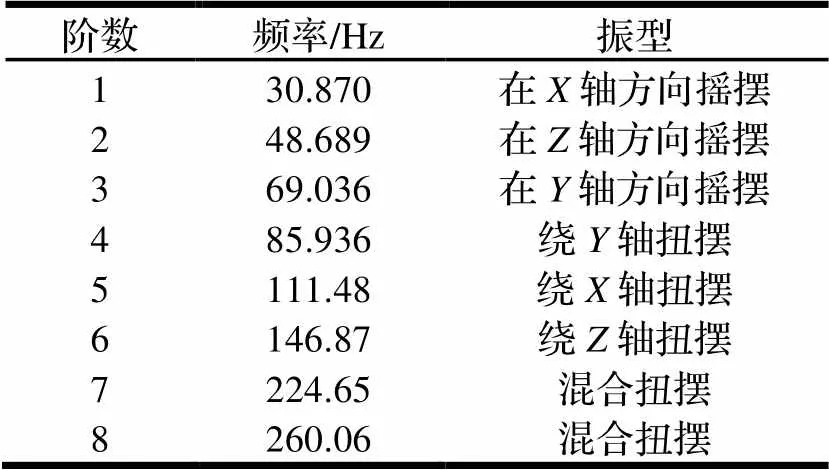
表2 模块化机械手的各阶固有频率
3 模块化机械手结构优化
3.1 分析及优化方案
经过现场分析,模块化机械手输入激励主要是来自6个轴伺服电动机通过减速器输入的转频。模块化机械手6个轴的伺服电动机的最高工作转速为3000 r/min。第1~3轴为RV减速器,减速比为120。第4~6轴为谐波减速器,最小减速比出现在第5和第6轴,减速比为103,两个轴减速器输入转速为29.13 r/min。经过计算,模块化机械手其他轴输出的转频都比这两个轴低,即远离模块化机械手结构第1阶固有频率(1=30.870 Hz)。根据模块化机械手的激励输入,再结合模块化机械手有限元分析前8阶固有频率来看,整个机械手结构系统的第1阶模态比较容易出现[10],所以本文只研究第5和第6轴的转频即可。
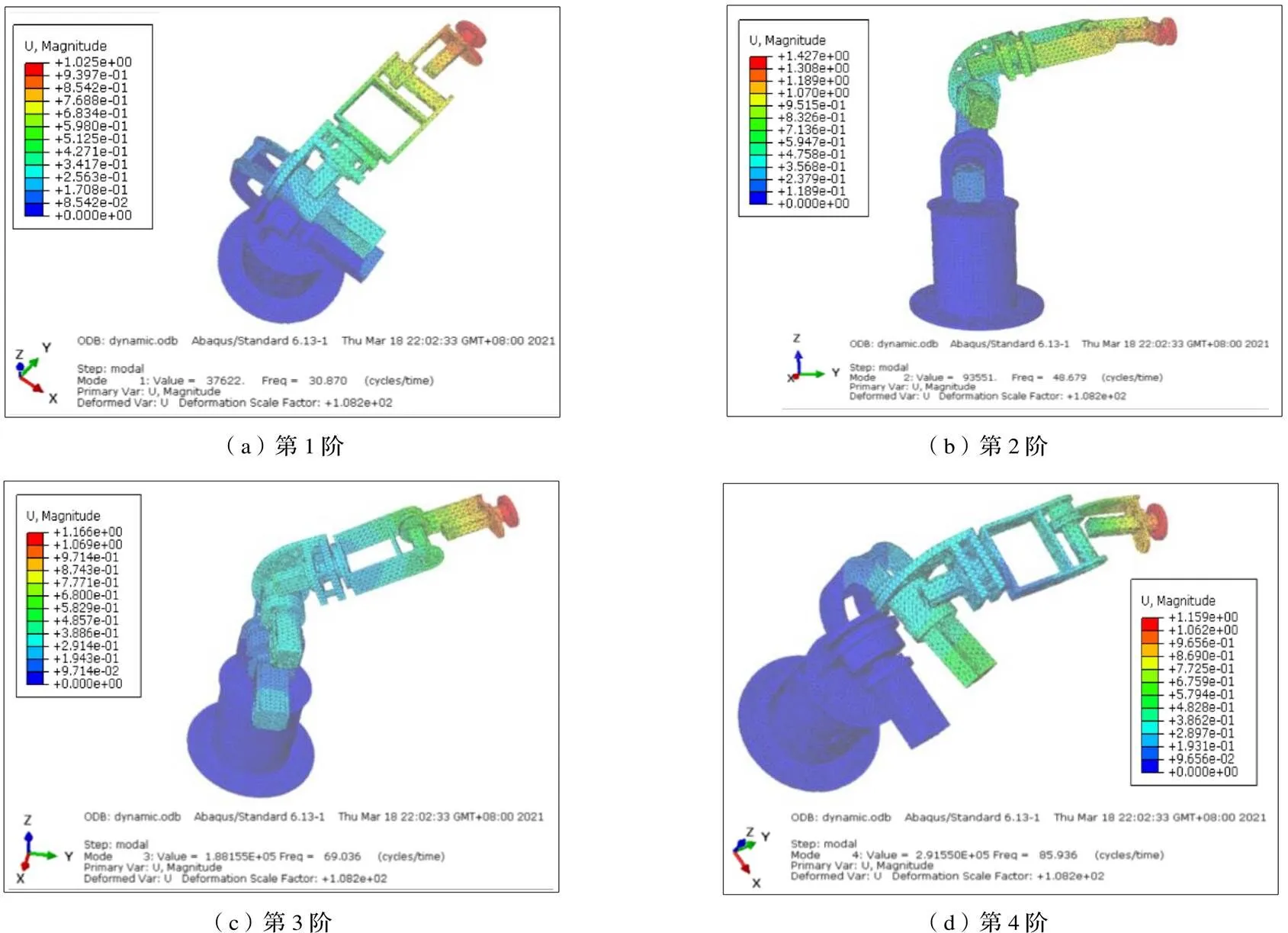
图6 模块化机械手的前4阶振型图

图7 模块化机械手的5~8阶振型图
由于第5和第6轴减速器的转频接近模块化机械手结构的第1阶固有频率,所以容易引起模块化机械手共振。通过对模块化机械手低阶振型和现场的观察,振动主要出现在第4~6轴处。目前,第6轴的电机只连接有一块铝板,可以在该位置上进行优化。在原来的基础上加一块铝板进行加固,使结构更结实,最重要的是能提高第1阶的固有频率。
3.2 验证优化方案
模块化机械手优化后,再利用ABAQUS进行模态分析。根据前面分析可知,主要振动是低阶引起的,所以只算出模块化机械手的前4阶固有频率和相应振型,如表3、图8所示。
模块化机械手的第1阶固有频率为36.033 Hz,比原来提高了16.72%,更加远离第5和第6轴减速器的转频,同时第6轴的结构强度也得到了提高。

表3 优化后模块化机械手的前4阶固有频率
4 结论
对模块化机械手进行静力学分析,模块化机械手在极限位置时,各轴部件应力值远小于材料的许用应力值,满足强度要求。第6轴连接法兰处的变形量最大,值为0.17 mm。本台模块化机械手是用于焊接,该最大变形量符合工作性质要求。通过对模块化机械手进行模态分析,得出其固有频率和相应振型。伺服电动机工作的最高转速为3000 r/min,第5和第6轴减速器的减速比为103,减速机输出转频为29.13 r/min,该转频接近模块化机械手结构的第1阶固有频率,容易引起共振。对第6轴的结构进行优化,验证结果表明:优化后模块化机械手第1阶固有频率提高了16.72%,避开了减速器的输入转频,防止共振。同时第6轴的结构强度也得到了提高。本研究为模块化机械手结构优化提供了理论依据。

图8 优化后模块化机械手的前4阶振型图
[1]兰虎,鄂世举. 工业机器人技术及应用[M]. 北京:机械工业出版社,2019:5-29.
[2]胡义华. 抓取机械手的动力学性能及结构有限元仿真[J]. 济南大学学报(自然科学版),2021,35(5):508-512.
[3]陈彦宇,田东庄,许翠华,等. 基于Abaqus桁架机械手动静态性能分析[J]. 煤矿机械,2017,38(11):58-60.
[4]崔书婉,韦建军. 焊接机器人的有限元分析与结构优化[J]. 制造业自动化,2014,36(20):67-70.
[5]赵军,殷鸣,赵秀粉,等. 基于UG的驱动桥壳动静态性能有限元分析与优化设计[J]. 机械,2017,44(1):5-10,50.
[6]吴凯佳,苏小平. 某工程车辆车架的结构动力学分析与优化[J]. 南京工业大学学报(自然科学版),2019,41(6):688-694.
[7]曹岩,沈冰,程文. ABAQUS 6. 14中文版有限元分析与实例详解[M]. 北京:清华大学出版社,2018.
[8]肖智勇,段建中,杜鑫强,等. Motoman工业机器人有限元静态分析及改进设计[J]. 长沙理工大学学报,2011(12):71-75.
[9]CAD/CAM/CAE技术联盟. ABAQUS 2016 有限元分析从入门到精通[M]. 北京:机械工业出版社,2017.
[10]李德葆. 振动模态分析及其应用[M]. 北京:宇航出版社,1989.
[11]汪永元. 工业机器人的系统分析与仿真研究[D]. 成都:西南交通大学,2014.
[12]陈祝权,梁晓合,林粤科,等. 六自由度串联机器人结构设计及有限元分析优化[J]. 机床与液压,2013,41(23):97-101.
Dynamic and Static Analysis and Structural Optimization of Modular Manipulator Based on ABAQUS
WANG Wenjun,LI Fusong,LIN Weijian
(College of Mechanical Engineering, Liuzhou Institute of Technology, Liuzhou 545000,China)
Large vibration of modular manipulator in some positions of welding process affects the precision and quality of welding. The modular manipulator is carried out static and dynamic analysis. Firstly, UG NX 12.0 is used to model the modular manipulator. Secondly, ABAQUS is used to carry out static analysis and modal analysis of the modular manipulator. The results of static analysis show that the structural stiffness and strength of the manipulator meet the requirements of working performance. The modal analysis show that the first natural frequency of the modular manipulator (1=30.870 Hz ) is very close to the input minimum frequency of reducer (29.13 r/min). It is easy to occur to resonance for the modular manipulator. The verification analysis is carried out for the optimization of the sixth axis of the modular manipulator. It shows that the first natural frequency of the modular manipulator is 36.033 Hz which 16.72% higher than the original one. It is far away from the input frequency of the reducer and avoids resonance. This study provides a theoretical basis for the improvement of modular manipulator.
modular manipulator;ABAQUS;natural frequency;resonance;structural optimization
TP241;TH113
A
10.3969/j.issn.1006-0316.2021.09.010
1006-0316 (2021) 09-0067-07
2021-03-25
广西高校中青年教师科研基础能力提升项目(2019KY1104)
王文军(1982-),男,广西田阳人,硕士,工程师,主要研究方向为机械结构设计、机械振动与测试技术,E-mail:39628608@qq.com。
