不等式中的任意与存在问题

孟方明

(浙江省春晖中学 312300)

一、一元不等式

1.任意问题

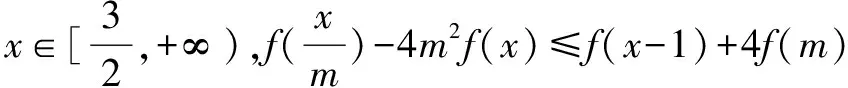
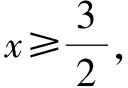
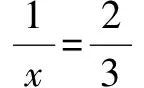
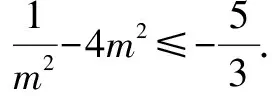
整理，得12m4-5m2-3≥0.

即(3m2+1)(4m2-3)≥0.

说明形如g(m)≥f(x)的不等式任意性问题，可转化为g(m)≥f(x)max；形如g(m)≤f(x)的不等式任意性问题，可转化为g(m)≤f(x)min.

2.存在问题

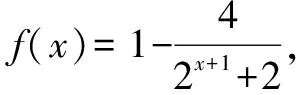
去分母，整理得m·(2x)2+(m-3)2x-1<0.

设2x=t，则t∈(1,2)且mt2+(m-3)t-1<0.

由mt2+(m-3)t-1<0，得m(t2+t)<3t+1.

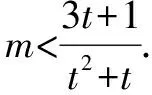
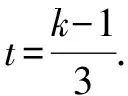
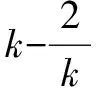
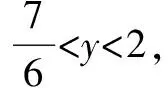
说明形如g(m)≥f(x)的不等式存在性问题，可转化为g(m)≥f(x)min；形如g(m)≤f(x)的不等式存在性问题，可转化为g(m)≤f(x)max.有的时候由于f(x)的最值不一定存在，还要注意所求范围的端点是否可取.

二、二元不等式

1.任意与存在搭台

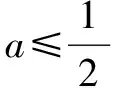
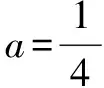
解析(1)略；

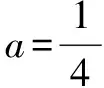
当x∈(0,1)时，因为f′(x)<0，所以f(x)单调递减；

当x∈(1,2)时，因为f′(x)>0，所以f(x)单调递增.

对于条件“对任意x1∈(0,2)，存在x2∈[1,2]，使f(x1)≥g(x2)成立”，不妨先固定x2，则只需要f(x1)min≥g(x2).

说明一般地，若对任意x1∈D1，存在x2∈D2，使f(x1)≥g(x2)成立，先求出无参函数的最值，如本题中，函数f(x1)无参， 固定x2，先求出f(x1)的最小值，得到f(x1)min≥g(x2)；再考虑“存在”，求出g(x2)的最小值，满足f(x1)min≥g(x2)min，或者视f(x1)min≥g(x2)为一元不等式处理.对任意x1∈D1，存在x2∈D2，使f(x1)≤g(x2)成立可类似处理.

2.任意与任意唱戏

例4 已知函数f(x)=(a+1)lnx+ax2+1.

(1)讨论函数f(x)的单调性；

(2)设a<-1，如果对任意x1,x2∈(0,+∞)，|f(x1)-f(x2)|≥4|x1-x2|，求a的取值范围.

解析(1)略；

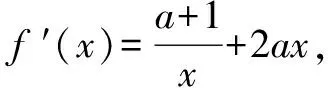
令g(x)=f(x)+4x，则上式等价于g(x)在(0,+∞)在单调递减.

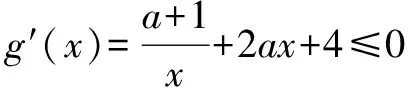
设t=4x+1>1，

由恒成立的意义知，只需a≤h(t)min.

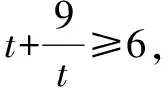
所以h(t)≥-2，

故a≤-2.

说明一般地，若对任意x1∈D1，任意x2∈D2，使f(x1)≥g(x2)成立，只需满足f(x1)min≥g(x2)max；若对任意x1∈D1，任意x2∈D2，使f(x1)≤g(x2)成立，则只需转化为f(x1)max≤g(x2)min.本题由于不等式的对称性，通过构造函数，利用单调性求解问题，其过程体现了将二元x1,x2减为一元x的重要思想方法.