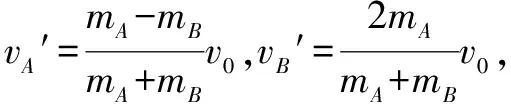变换视角谈碰撞 统一模型巧解题

胡永琰

(福建省上杭县第一中学 364200)

一、即时碰撞

对于“碰撞”这部分内容，高中教材主要是讲一维的正撞，从正碰中能量的观点进行分类：弹性正碰、非弹性正碰以及完全非弹性正碰.碰撞时，相互作用时间极短，内力远大于外力，因此满足系统动量守恒.如图1所示：整个碰撞过程可以拆分为“接近过程”和“分离过程”.在教学中，应该认真引导学生剖析碰撞过程，强化物理过程分析，切忌死记硬背，唯有让学生深刻理解了碰撞现象的本质和特征，才能在各种碰撞情境中灵活处理相关问题.

图1

例1在光滑水平面上有两个相同的弹性小球A、B质量都为m， 现B球静止，A球向B球运动，发生碰撞，已知碰撞过程总机械能守恒，两球压缩最紧时的弹性势能为Ep，则碰撞前A球的速度？

评析此题重点考察碰撞过程的分析，显然，把A、B两球的碰撞拆分成“接近”和“分离”两个过程，不难发现，两球接近过程中A减速、B加速，当两球速度相等的时，系统的弹性形变最大，获得的弹性势能最大.由此应用能量和动量观点便可求解.此外，因为碰撞作用时间极短，笔者又把这种碰撞称为“即时碰撞”，相关归纳如下，此类碰撞也是学生最熟悉的，如图2.

图2

此类碰撞问题的解题策略:

(1)抓住碰撞的特点和不同种类碰撞满足条件，列出相应动量守恒和能量守恒方程求解.

(2)涉及“一动碰一静”模型，两物体发生弹性正碰的动量守恒和能量守恒方程如下：

m1v1=m1v1′+m2v2′

①

②

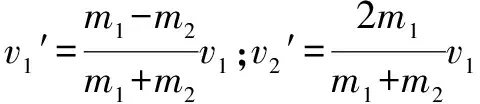
对于碰后的两球的速度，应熟记起来，可以在处理此类题目中提高解题效率.

(3)“一动碰一动”模型中，两物体发生弹性正碰的动量守恒和能量守恒方程如下：

m1v1+m2v2=m1v1′+m2v2′

①

②

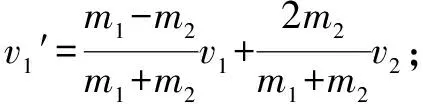
例2(15·全国Ⅰ卷)如图3，在足够长的光滑水平面上，物体A、B、C位于同一直线上，A位于B、C之间.A的质量为m，B、C的质量都为M，三者都处于静止状态，现使A以某一速度向右运动，求m和M之间满足什么条件才能使A只与B、C各发生一次碰撞.设物体间的碰撞都是弹性的.

图3

解析根据题意,以时间为线索展示相应的物理过程，如图4：

图4

具体解答如下：

A和C碰撞：由能量守恒得：

①

由动量守恒得：mvA=mvA′+MvC′

②

③

④

依题意：A和C碰撞后要反弹，则有vA′<0

⑤

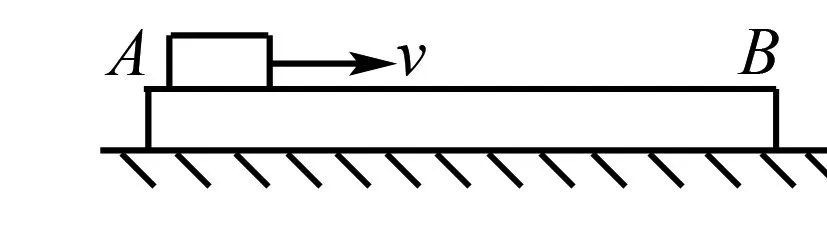
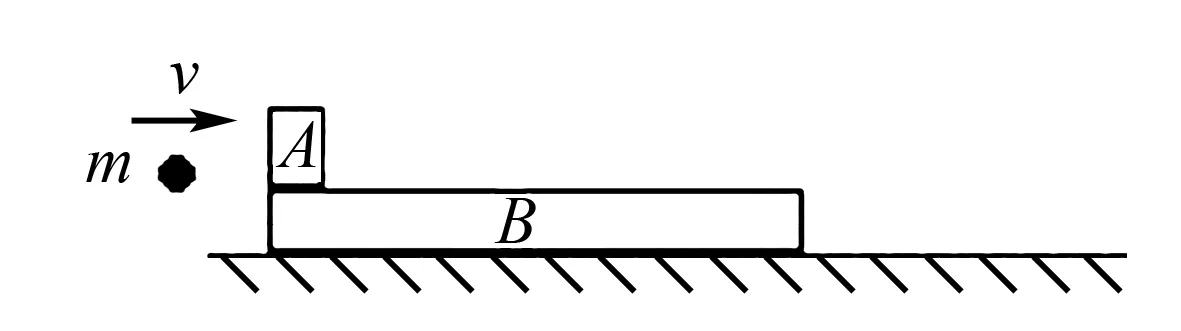
由③⑤易得m

A和B碰撞：由能量守恒得：

⑥

由动量守恒得：mvA′=mvA″+MvC′

⑦

⑧

因为A只与B、C各发生一次碰撞

所以有：vA″≤vC′

⑨

评析综合“能量”和“动量”的观点依序剖析各物理过程，列出各自的能量和动量方程，根据熟知的“一动一静”模型的相关结论，就可以条理清晰、快速高效地破解这类题目.

二、慢碰撞

1.构建“慢碰撞”模型，巧解“弹簧——滑块”类问题

在某些情境中，涉及的物理现象表象看来并非是“碰撞”现象，但细推其物理过程，与碰撞过程完全一致.如图5：在光滑的水平面上，有A、B两球和一轻弹簧，A、B两球的质量分别为m1、m2，B与轻弹簧右端连在一起以速度vB向右运动，A以速度vA撞向弹簧(vA>vB),从状态1到状态2的过程，因弹簧形变明显，较之于“即时碰撞”作用时间比较长，但本质就是放慢了的完全非弹性碰撞而已，因此笔者在此称之为“慢碰撞”.同理，从状态1到状态3的过程就是一个放慢的完全弹性的碰撞.如此，就可以把这类模型化归到熟知的碰撞模型中，进而可以灵活运用“一动碰一静”、“一动碰一动”弹性正碰的相关结论了，巧解相关问题.

状态1：弹簧处于原长状态 状态2：弹簧压缩至最短 状态3：弹簧恢复原长图5

例2如图6，左端固定着轻弹簧的物块B静止在光滑的水平面上，物块A以速度v0向右运动，通过弹簧与物块B发生正碰，已知物块A的质量大于B的质量，当弹簧压缩到最短时，下列说法正确的是( ).

图6

A.弹簧原长的时候B的速度最小

B.A、B速度相等的时候A的速度最大

C.A、B速度相等的时候A与B的机械能最小

D.A、B分离时A、B的运动方向相反

例3如图7，用轻弹簧相连的质量均为2kg的A、B两物块都以v=6m/s的速度在光滑水平地面上运动，弹簧处于原长，质量4kg的物块C静止在前方，B与C碰撞后二者粘在一起运动．在以后的运动中，求：

图7

(1)当弹簧的弹性势能最大时，物体A的速度多大？

(2)弹性势能的最大值是多大？

(3)A的速度有可能向左吗？为什么？

解析B与C发生即时碰撞粘在一起，此后，A、弹簧及BC粘连体构成了“慢碰撞”模型，根据碰撞特点知：当A与BC共速时，弹性势能最大，由系统动量和能量守恒易得A的速度和弹性势能的最大值.由“慢碰撞”过程可知：从A开始压缩弹簧到弹簧恢复原长的过程中，弹簧弹力始终向左，因此，当弹簧到弹簧恢复原长的时刻A的速度最有可能向左，故只需算出此时A的速度情况即可判断.此外，认真分析从A开始压缩弹簧到弹簧恢复原长的过程，便会发现A与BC粘连体构成了“一动碰一动”的弹性正碰模型.根据相关结论，可快速得到A的速度.

点评引入“慢碰撞”模型后，就可以从“碰撞”的角度来处理弹簧——滑块类问题，从“动量和能量”两个视角切入，把相关碰撞模型特点及有关结论迁移应用到此情境中来，便可科学有序地求解相关问题.

2.构建“慢碰撞”模型，巧解“滑块——木板”类问题

如图8，滑块A以一定的初速度v滑上粗糙的长木板B上，长木板B与地面光滑接触，A、B通过系统摩擦内力的作用下，分别做减速和加速运动，若长木板B足够长，易得A、B最终达到共速且以共同速度做匀速直线运动.整个物理过程就如放慢的完全非弹性碰撞，只不过系统损失的动能以摩擦生热的内能呈现而已.如此，在处理这类“滑块——木板”问题时也可以构建碰撞模型，再用非常熟悉的“动量和能量”的观点求解问题，提高解题效率.

图8

图9

(1)A与B相对静止时的速度

(2)木板B至少多长，A才不至于滑落.

解析小球与A发生即时碰撞，根据即时碰撞特点：只与直接作用的物体有关，内力远大于外力.此时小球与A构成系统动量守恒，与B无关.A与小球即时碰撞后获得一定初速度，此后，A与B发生完全非弹性慢碰撞，依次列出系统的动量守恒和能量守恒方程，便可求得相关物理量.

点评同理，引入“慢碰撞”后，可从“碰撞”的角度来处理“滑块——木板”类问题，亦是强化“动量和能量守恒”观念解决问题的过程.

综上例谈中可见：从“作用时间”上把碰撞又分成“即时碰撞”和“慢碰撞”两种模型，特别是在引入“慢碰撞”模型后，可以把“滑块——弹簧”、“滑块——木板”这类情境统一化归到“碰撞”模型中来，再用熟知的“碰撞”问题的通性通法来解决，进而可以精准、高效地求解相关问题.

教学中，应当引导学生加强对物理概念和物理规律的内涵的理解，强化建模能力，通过物理模型实现物理规律与物理现象的关联与对接.同时注意物理模型的相关性, 通过不同物理模型进行类比 、延展 、拓宽, 找出其共性和个性, 建立系统化的物理规律转化系统，进而能快捷有效地处理实际问题.