特殊法妙解客观题
2021-09-27田峰
田 峰
(安徽省合肥方了个田教育科技有限责任公司 230031)
在解答高考数学客观题时,由于客观题本身的属性,我们可以采取一般与特殊之间相互转化的思想,借助特殊法,根据题目条件选取对应的数值、函数、角度、点、图形等形式来特殊处理.特殊法处理,回归一般性,简单易操作,方便且快捷,是破解数学客观题中的一种不可多得的好办法.下面结合数学客观题实例,对一些常见的特殊法加以巧妙应用.
一、特殊值法
特殊值法经常应用于一些涉及函数、不等式、方程、算法等客观题中,借助特殊值的选取,代入验证相应的函数、不等式、方程、算法等问题,结合对应的选项加以排除.

A.(-∞,-1] B.(0,+∞)
C.(-1,0) D.(-∞,0)
分析对于分段函数与不等式问题,可以借助特殊值的选取,借助排除法来处理,从特殊到一般,结合对应的选项来处理.特殊值法比常规的函数图象法的应用显得更加简单快捷.
解析令x=-1,可得f(x+1)=f(0)=2-0=1,f(2x)=f(-2)=22=4,显然f(x+1) 点评由于涉及分段函数中的不等式解集的确定性,借助特殊值的选取,直接有效,很好地回避了分段函数的图象与性质以及不等式的求解等问题.在实际处理过程中,要结合选项中的不同取值情况,合理确定特殊值,可以使得问题的正确判断更加快速,适当减少特殊值的取值次数与验证. 特殊函数法经常应用于一些涉及抽象函数、大小比较等的客观题中,借助特殊函数的选取,使之满足题目条件,化抽象为具体,再利用特殊函数进一步发现规律,尝试寻找问题的突破点. 例2 已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=( ). A.-50 B.0 C.2 D.50 分析常规方法是根据题目条件来分析确定抽象函数f(x)的周期性以及相应函数式的值,有一定的运算量.而根据题目条件寻找与之对应的特殊函数,直达要害,一步到位,简单易操作. 则有f(1)+f(2)+f(3)+f(4)=2+0-2+0=0. 所以f(1)+f(2)+f(3)+…+f(50)=12×0+f(49)+f(50)=f(1)+f(2)=2.故选C. 点评在选取特殊函数处理一些数学客观题时,往往从函数的单调性、奇偶性、周期性、对称性等角度来分析,选取常见的基本初等函数,性质易判断与对应,条件比较容易满足. 特殊角度法经常应用于一些涉及平面几何、平面向量、三角函数等客观题中,借助特殊角度的选取,可以使得平面几何或平面向量的图形直观化,或数形结合,或回避三角函数中三角恒等变换的繁杂步骤,简化过程. 例3 已知sinα+cosβ=1,cosα+sinβ=0,则sin(α+β)=____. 分析结合题目条件,通过选取特殊角度使一般性问题特殊化,在特殊情况加以运算,再对特殊情况下的运算结果一般化即可. 点评要直接求解需要涉及有关三角函数的性质以及三角恒等变换公式等,相比来说比较复杂.而通过选取特殊角度,省去繁杂的三角恒等变形公式及其应用,选取合理的特殊角度是快捷破解问题的关键. 特殊点法经常应用于一些涉及函数图象、平面向量、平面解析几何等客观题中,借助特殊点的选取,能巧妙处理函数图象、平面向量的相关运算、直线与圆或圆锥曲线的位置关系等问题,更加直观快捷,易处理,妙判断. 例4下列函数中,其图象与函数y=lnx的图象关于直线x=1对称的是( ). A.y=ln(1-x) B.y=ln(2-x) C.y=ln(1+x) D.y=ln(2+x) 分析常规方法是根据函数的图象与性质,并结合对称性质来处理.而根据题目条件通过特殊点的选取,以点代线,以特殊代一般,可以更为快捷确定相应的函数关系式. 解析由于函数图象的对称就是图象上的每个点的对称问题,在函数y=lnx的图象上取一特殊点(1,0),其关于直线x=1的对称点也是(1,0),结合各选项中的函数,只有选项B中的函数y=ln(2-x)过该点,故选B. 点评通过选取特殊点,从特殊点入手,以点代线,以特殊来代一般,实现问题的快捷破解.巧妙选取特殊点,借助点的变化来推广到一般性的变化. 特殊图形法经常应用于一些涉及函数的基本性质、平面几何、解三角形或平面向量、立体几何等的客观题中,借助特殊图形的选取,往往是特殊函数图象的构建、特殊平面几何图形的应用、特殊立体几何图形的切入等,直观形象,易于操作与判断. 例5已知函数f(x)=2sinx+sin2x,则f(x)的最小值是____. 分析常规方法是利用三角关系式,通过三角函数图象与性质、三角恒等变换、基本不等式等方法来处理,难度非常大,不易操作.借助单位圆这一特殊图形的构造,把函数关系式与三角形面积加以有机链接,合理转化,巧妙推理,进而确定函数的最值问题. 解析如图1所示,构造特殊图形——单位圆,其中A(-1,0),B,C关于x轴对称,可设B(cosx,sinx),则有C(cosx,-sinx),D(cosx,0). 点评原问题的处理比较繁杂.而借助单位圆这个特殊的平面几何图形的构造,结合单位圆中内接三角形面积的性质,合理构建对应的不等式,实现有机链接,直观转化,省去三角函数中众多公式的应用与推理,很好地提升解题效益. 特殊法是破解一些高考客观题的最佳方法之一,充分体现“小题小做”或“小题巧做”的解题策略,借鉴解题经验,通过特殊的数值、函数、角度、点、图形等特殊法的选取与应用,实现简单快捷处理,巧妙安全判断.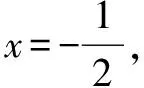
二、特殊函数法

三、特殊角度法

四、特殊点法
五、特殊图形法


