数形结合思想在三角函数中的应用
2021-09-27刘大鹏
数理化解题研究 2021年25期
刘大鹏
(辽宁省黑山县第一高级中学 121400)
一、关于三角函数线的一些基础知识
1.三角函数线的概念
单位圆中某些有向线段的长度和方向可以用来表示三角函数值,称它们为三角函数线.
注意:用字母表示这些线段时,特别要注意表示起点的字母写在前面,而表示终点的字母写在后面,它们的顺序不能颠倒.
2.三角函数线的方向
规定:凡是从原点出发的线段,以原点为起点;不从原点出发的线段,以三角函数线与坐标轴的交点为起点.
3.三角函数线表示的三角函数值的正负的规定
(1)正弦线、正切线的方向与纵轴一致,向上为正,向下为负.
(2)余弦线的方向与横轴一致,向右为正,向左为负.
二、应用三角函数线解题
1.比较同名不同角函数值的大小或比较同角不同名函数值的大小或既不同名也不同角的函数值的大小



2.巧求三角函数值
例2 tan255°=( ).
解析利用诱导公式和正切线,得tan255°=tan75°>tan45°=1.故选D.
说明本题的解法充分利用选项提供的信息,结合诱导公式、正切线很好地解决了我们不会精确求tan255°的值的问题.

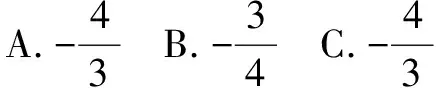


3.解三角方程或三角不等式(组)




4.求三角函数的值域
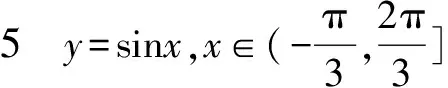
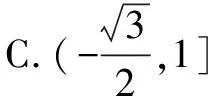
答案:选C.
说明如果不画三角函数线也不画正弦图象,很容易误选B.
5.巧妙地解决某些三角问题

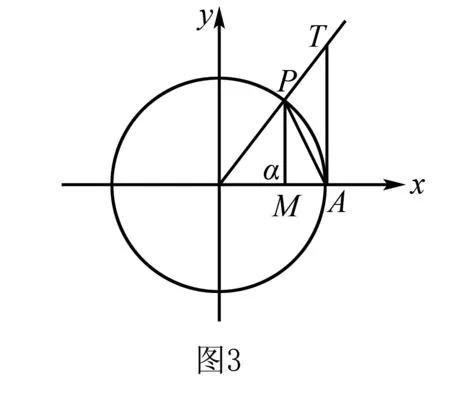


所以sinα<α 例7 已知A(cos20°,sin20°),B(cos80°,sin80°),求|AB|. 解析A,B是单位圆上两点,连接OB,OA,AB,知△ABO是正三角形,所以|AB|=1. 例8 求sin18°的值. 例9 写出如图5所示函数y=Asin(wx+φ),(A>0,w>0)的解析式.三、利用数轴或单位圆或其它图形解题


四、利用所给图象求正弦型函数解析式y=Asin(ωx+φ)+b