一类非奇异H-矩阵判定的充分条件
2021-09-27杨亚芳梁茂林
杨亚芳,梁茂林
(天水师范学院 数学与统计学院,甘肃 天水 741001)
1 预备知识
H-矩阵在数学,物理,控制论及经济数学等许多领域有着重要的研究价值和实用价值.对H-的判定许多作者给出了一些研究成果[1-6].本文用比较矩阵元素的方法,给出了判定非奇异H-矩阵的一组新条件,改进了已有的一些判定方法.
用Cn×n表示n复矩阵的集合.设A=(aij)∈Cn×n,对∀i,j∈N={1,2,…,n},记
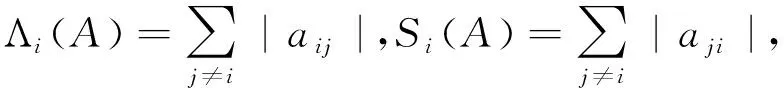
定义1[1]设A=(aij)∈Cn×n,若存在α∈(0,1],使得|aii|≥Ei,则称A为α-对角占优矩阵;若|aii|>Ei,则称A为严格α-对角占优矩阵,记为A∈D(α);若存在正对角矩阵X,使得AX∈D(α),则称A为广义严格α-对角占优矩阵,记为A∈D*(α).
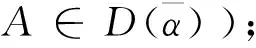
引理1[3]设A=(aij)∈Cn×n,α∈(0,1],则A非奇异H-矩阵(记作A∈D)当且仅当A∈D*(α).
引理2[1]设A=(aij)∈Cn×n,若A为不可约α-对角占优矩阵,或A为具有非零元素链的α-对角占优矩阵,则A∈D.
另记
N1={(i|0<|aii|=Ei},N2={(i|0<|aii| 则N=N1⊕N2⊕N3.易知,若N1∪N2=∅,则A∈D; 若N3=∅,则A∉D; 因此常假设N1∪N2≠∅,N3≠∅.定义 易知Pi(A)≤Ei<|aii|, 且 根据文[7]中引理1,本文中总假设Λi(A)≠0,Si(A)≠0,i=1,2,…,n.另记 i∈N2, 定理1 设A=(aij)∈Cn×n,α∈(0,1],且I1(A)=∅,若i∈N2, (1) 成立,则A∈D. (2) (3) 记 (4) (5) (6) 构造D=diag{d1,d2,…,dn}, 其中 记B=AD=(bij),下证B∈D(α). αΛi(B)+(1-α)Si(B) |bii|-αΛi(B)-(1-α)Si(B) 综上所述,|bii|>αΛi(B)+(1-α)Si(B),(i∈N),即B∈D(α),因此A∈D. 注由于 i∈N2. 故本文定理1包含了文献[4]的定理1,因此改进了文献[4]中的主要结果. 定理2 设A=(aij)∈Cn×n,α∈(0,1], 且A不可约,如果i∈N2, (7) 记I2(A)={i∈N2|使(7)式中等号成立了},且N1∪N2I2(A)≠∅,则A∈D. 三是结合实际工作及时给予员工精神鼓励。既要表扬团队,又要逐一表扬每位员工的比较优势,要让员工觉得自己对于团队很重要,有一种“主角”的感觉,充分发挥优秀员工的模范带头作用,从而实现整个团队共同进步。 构造对角矩阵D=diag{d1,d2,…,dn},令B=AD=(bij),其中 αΛi(B)+(1-α)Si(B) ∀i∈N2, 由(6)知 αΛi(B)+(1-α)Si(B) ∀i∈N3, |bii|-αΛi(B)-(1-α)Si(B) ≥0. 定理3 设 证明类似定理2的证明可得B=AX=(bij)满足|bii|≥αRi(B)+(1-α)Si(B)(∀i∈N),且上式中每个等号成立的i必然属于集合I2(A)∪(N1I1(A))∪(N3I3(A)), 而当i∈I2(A)∪(N1I1(A))∪(N3I3(A))时必有aij1aj1j2…ajk-1k≠0, 满足k∈I1(A)∪(N2I2(A))∪I3(A), 易知这样的k必有 |bkk|≥αRk(B)+(1-α)Sk(B)(k∈N). 由引理2知A∈D. 注:当式(7)成立时,|bii|≥αRi(B)+(1-α)Si(B)(∀i∈N)成立,集合I2(A)∪(N1I1(A))∪(N3I3(A))包含了所有使得式(7)中等号成立的指标i,而集合I1(A)∪(N2I2(A))∪I3(A)包含了所有使得式(7)中大于号成立的指标i. 例1 设 取α=0.8, 则N1={1},N2={3},N3={2,4,5}.计算得 即矩阵A满足定理1的条件,因此矩阵A为广义严格α-对角占优矩阵. =2.3333, 所以不满足文献[4]的条件. 又 所以无法用文献[5]去判定.经计算得文献[6]中的M3=3.4167, 故不能由文献[6]来判别. 注:文献[4]中,当矩阵满足条件 时为非奇异H-矩阵.在文献[6]中,当矩阵满足条件 时为非奇异H-矩阵.在例1 中这些条件显然都是不满足的.由此看出本文定理丰富了非奇异H-矩阵的判定理论.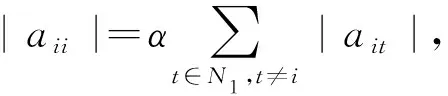
2 主要结果
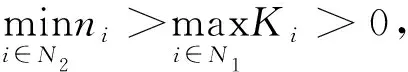
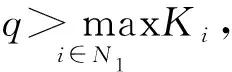
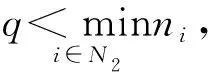
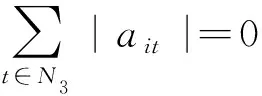
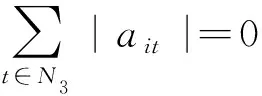
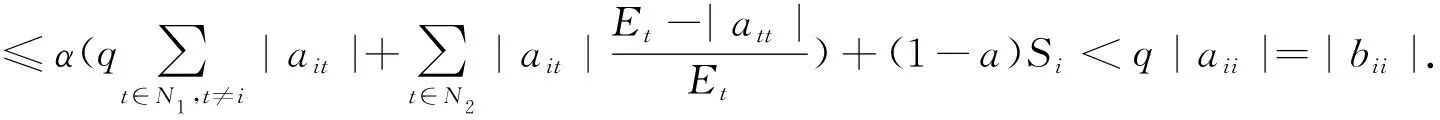
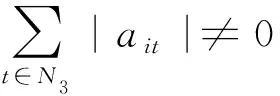
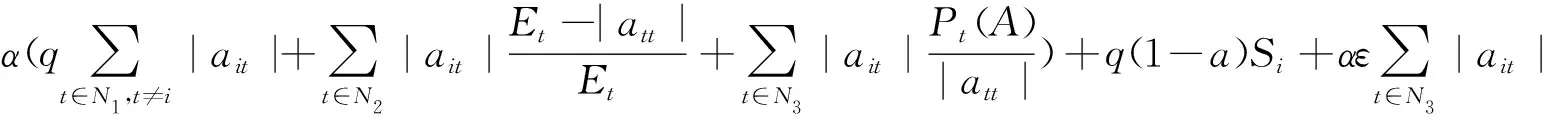


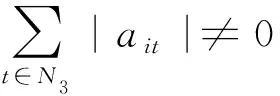
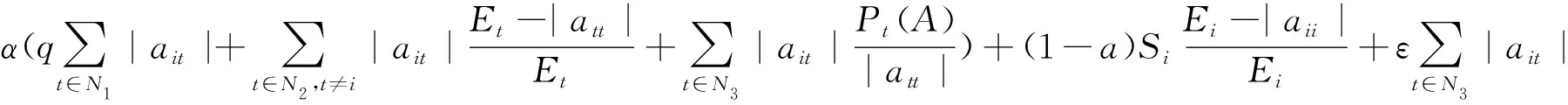
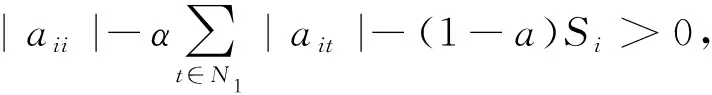
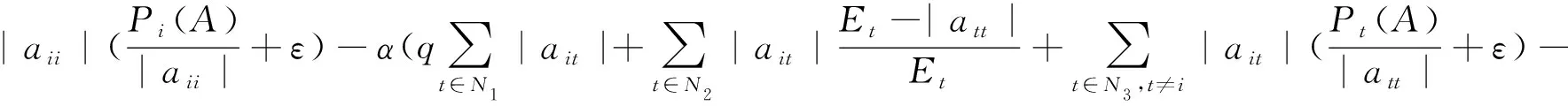
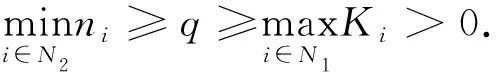

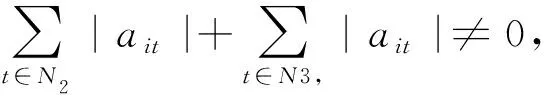
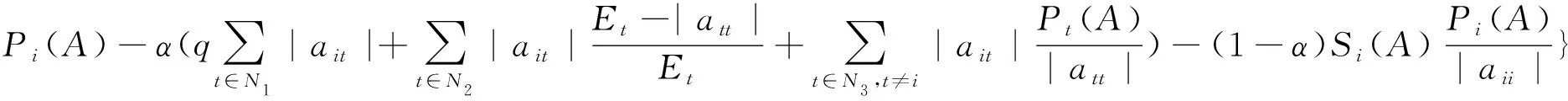
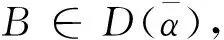
3 数值例子