结构面位置对于深部高应力采动硬岩巷道破坏的影响
2021-09-26冯帆赵兴东陈绍杰李夕兵李地元黄万朋
冯帆,赵兴东,陈绍杰,李夕兵,李地元,黄万朋
(1.山东科技大学能源与矿业工程学院,山东青岛,266590;2.东北大学资源与土木工程学院,辽宁沈阳,110819;3.中国矿业大学(北京)深部岩土力学与地下工程国家重点实验室,北京,100083;4.中南大学资源与安全工程学院,湖南长沙,410083)
大量工程实践表明,深部岩体动力灾害的发生不仅与应力场特征和开采扰动有关,而且与其赋存的地质构造密切相关[1−3]。由于深部地下工程岩体处于“三高一扰动”(高地应力、高地温、高渗透压以及强烈开采扰动)的复杂地质力学环境之中,在含有结构面岩体附近进行采掘工程时,开采扰动与结构面的相互作用会导致其周围岩体应力场、位移场再次发生变化,进而诱发更大规模的矿井灾害[4−8],一些硬性结构面在顶板垮落发生后被暴露出来,在结构面顶端形成V 型破坏。即使该巷道采用了特定的锚网支护,结构面附近岩体仍然发生明显破坏,表明此时破坏程度较为严重。开采扰动是导致巷道破坏的外在诱导因素,而结构面周边非均匀应力场、位移场的存在则是其内在因素。
为了调查结构面对于深部巷道稳定性的影响,国内外诸多学者采用室内试验和数值模拟开展了广泛研究。周辉等[6]结合锦屏二级水电站引水隧洞,分析了不同结构面类型、力学性质、产状、施工方法条件下结构面对岩爆的作用机制,并从定性的角度将结构面型岩爆划分为滑移型、剪切破裂型和张拉板裂型。MANOUCHEHRIAN等[9]采用Abaqus 数值模拟软件对圆形巷道的结构面型岩爆机制进行了研究,研究结果表明:当巷道围岩内部赋存有结构面时,随着时间的推移,巷道围岩破坏范围呈现非线性的增长趋势。HUANG等[10]采用物理模拟以及数值模拟手段分析了弱面倾角、位置、厚度等对于巷道围岩破坏模式的影响,并建立了软弱夹层各参数与诱导损伤区之间的关系。周军华等[11]利用颗粒流模拟程序,对存在不同裂隙形态(长度、位置和倾角)的含孔洞岩样在单轴压缩下的力学性质进行数值试验研究,分析岩样破裂与力学特征随裂隙形态的变化情况,并探讨其损伤演化特性。CHEN等[12]采用数值模拟手段研究了结构面倾角与长度对深部硬岩巷道围岩裂纹扩展行为、破坏模式、能量演化和位移分布的影响。张元超[13]采用物理模型试验及数值模拟对含圆形孔洞节理岩体的力学行为进行研究,探讨了不同节理岩体结构参数(节理倾角、间距、连续度等)及不同应力状态对孔洞及节理围岩的强度、变形和破坏行为的影响规律。FENG等[14]采用数值模拟研究了结构面作用下深埋高应力硬岩巷道破坏特性与机制,分析了结构面倾角、位置、摩擦效应等对于巷道破坏的影响。朱飘扬[15]结合室内试验、数值模拟和理论研究当孔洞周围存在邻近裂隙时,在受压状态下的裂隙扩展和破坏模式。
综上所述,当前国内外学者在研究结构面作用下深部高应力硬岩巷道破坏特性时,往往将结构面位置视为一项重要影响因素。然而,以往的研究大多是从定性的角度来分析结构面距离对于巷道围岩破坏的影响。同时,不同结构面位置条件下深部采动硬岩巷道的岩爆特性以及岩体内裂纹扩展行为也尚不明确。为此,本文作者采用有限元/离散元耦合数值模拟技术,分析不同结构面位置条件下深部采动硬岩巷道的裂纹扩展行为、能量演化规律与应力位移分布特征;以不同结构面长度下的临界相对距离为切入点,研究巷道围岩开挖卸荷效应与结构面活化效应之间的互动机制;最后,根据不同初始地应力状态(最大主应力方向),探讨结构面位置对于深部采动硬岩巷道稳定性的影响。
1 基于FEM/DEM的数值模型
有限元/离散元耦合分析方法(FEM/DEM)结合了连续和非连续数值方法的优点,能够同时模拟完整岩体以及在采用断裂力学的相关准则后新生裂纹的萌生和扩展全过程[16],在使用与物理学问题无关的数学覆盖问题时为连续和不连续问题提供了一个统一的框架。该方法已被广泛用于模拟岩石裂纹扩展研究中[17−18]。本文采用Rockfield Software 公司的ELFEN 软件进行有限元/离散元数值模拟分析。
1.1 数值模拟验证
为了揭示深部高应力硬岩力学破坏特性,以山东黄金红岭铅锌矿为工程背景,取深部大理岩作为研究对象[12]。为了验证所选择数值模拟方式的准确性与合理性,对大理岩试样进行了单轴压缩试验,并将试验结果与数值模拟结果进行了比较。
试样直径×长度为50 mm×100 mm。在数值模拟中,对试样顶部端面施加位移控制荷载。底部端面在y方向固定。本构模型采用转动裂纹Mohr-Coulomb 模 型(Mohr-Coulomb with rotating crack),该模型基于HAJIABDOLMAID 等[19]提出的黏聚力弱化内摩擦角提升模型(CWFS)计算残余强度参数(残余黏聚力和内摩擦角),能够很好地表征脆性岩石材料的破坏特性。为了能够较为真实地反映天然岩石的本质属性,数值模拟还考虑了岩石的非均质性。材料的非均质性应用于基础单元之上,允许每个单元都可以具有独立的弹性模量、泊松比、密度、抗拉强度和断裂能等。在ELFEN 软件中,首先对某一平均值设定上下限,并应用随机生成器为每个元素创建各属性的值。断裂能是ELFEN 软件中非常重要的参数之一,与极限应力强度因子有关,I 型断裂韧度KIC与断裂能Gf的关系为[20]

式中:KIC为I 型断裂韧度;E为弹性模量。I 型断裂韧度与间接抗拉强度σt的关系为[21]

根据式(1)和(2)可得大理石断裂能为5 N/m。岩石物理力学和离散接触参数如表1所示。

表1 大理岩数值模拟的材料参数[12]Table 1 Material parameters adopted in numerical simulation of marble[12]
图1所示为单轴压缩下大理岩破坏模式室内试验与数值模拟对比图。从图1可见:试样内部均出现了一条沿对角线方向的宏观剪切带。在剪切带周边还衍生出一系列拉伸裂纹,这些裂纹基本平行于最大主应力方向,表明试样的破坏模式为张拉−剪切型混合破坏。另外,从图1(b)可见:宏观剪切带是由一系列微小的拉伸裂纹所组成,这是由于试样具有较大的高度使得张拉型裂纹在加载方向一定位置处停止扩展与贯通[22]。这进一步证实单轴压缩下硬岩破坏的本质为张拉型破坏。对比分析室内试验与数值模拟结果发现,二者破坏模式具有较高的一致性,因此验证了该数值模拟的准确性与有效性。

图1 单轴压缩下试样破坏模式对比Fig.1 Comparison of failure mode under uniaxial compressive tests
1.2 数值模型建立
模型的几何结构如图2所示。对于平面应变,ELFEN 软件数值模拟假定模型的厚度为单元厚度(1 mm)。在试样中心部位设有一个圆形巷道,用于模拟开挖卸荷过程。模型外部长×宽为40 m×40 m。根据岩石力学理论,巷道开挖后应力集中区范围为开挖半径的3~5倍。因此,模型外部边界的长度至少应为巷道直径的10 倍,以排除巷道围岩应力重分布所产生的边界效应,故将巷道直径设置为4 m是合理的。在动态开挖卸荷过程中,当卸载应力波传播至边界时,在模型边界可能会产生一系列反射拉伸波并逐渐扩展至巷道周边岩体。为了消除反射拉伸波对数值模拟结果的影响,在数值模拟中采用了软件自带的“non-reflecting boundary”边界条件功能,使巷道开挖卸荷所产生的应力波通过边界而不被反射,从而保证数值模拟结果的正确性。
在实际地下工程中,巷道周边结构面往往是随机分布的。数值模拟方案中,在圆形巷道右侧布置了3条闭合裂隙(摩擦因数为0.1),以表示多条结构面。为了简化模型,仅在圆形巷道一侧布置结构面,且各结构面相互平行,如图2所示,其中,l为结构面长度;d为结构面左侧与巷道右侧边界的相对距离,d=0.6~5.6;λ为侧压力系数。3种结构面长度分别为2,4和8 m;根据初始地应力的不同,将侧压力系数分为0.45(垂直应力45 MPa,水平应力20 MPa,结构面与最大主应力不同侧)和2.25(垂直应力20 MPa,水平应力45 MPa,结构面与最大主应力同侧)2 种情况。当垂直应力为45 MPa和20 MPa 时,所对应的埋深约为1 500 m和700 m[23],因此,本文所设定的应力状态能够描述深部岩体工程力学特性。

图2 模型几何尺寸和边界条件Fig.2 Model geometry and boundary conditions
1.3 加卸载应力路径
对于平面问题,采用面力对模型边界施加初始地应力,即在模型顶部施加垂直应力P,在模型两侧施加水平应力λP,同时对底部y方向进行约束。采用线性位移控制方式加载,历时0.01 s,0.01 s后,保持应力始终不变,如图3(a)所示。
在建模过程中,将模型分为2 个实体(object),即圆形巷道以及除此以外的岩体。开挖卸荷过程被施加于圆形巷道实体上。采用线性卸载的方式,卸荷方程曲线如图3(b)所示。图中,荷载因子为1表示圆形巷道未开挖卸荷前的应力状态,荷载因子为0表示圆形巷道边界应力已被全部释放。由图3(b)可以看出:卸荷从开挖0.01 s 开始,当达到0.015 s 时,卸荷过程结束,表示圆形巷道已被全部开挖。采用线性卸荷方程曲线的目的是为了避免瞬间的开挖卸荷(应力改变)引起的突然破坏。开挖卸荷后岩体仍然会发生破坏,因此设定当模拟计算达到0.02 s时结束。

图3 加卸载路径(λ<1)Fig.3 Loading and unloading path(λ<1)
2 数值模拟结果分析
2.1 无结构面时采动巷道破坏
为了与含有多结构面时的数值模拟结果进行比较,考虑不含有结构面时的情况。无结构面时巷道围岩破坏最大主应力云图如图4所示。由图4可知:裂纹的起裂位置总是处于圆形巷道两帮靠近开挖边界处。由所施加的地应力可知,最大切向应力主要集中于巷道两帮围岩。仔细观察发现,巷道周边所形成的裂纹大多平行于开挖面[24−27],这与LI 等[28]在室内试验中观察到的板裂化破坏现象较为相似。另外,图4中巷道右侧的破坏程度比巷道左侧较为严重,这主要是由于岩石材料的非均质性所致。

图4 无结构面时巷道围岩破坏最大主应力云图Fig.4 Maximum principal stress contour of tunnel failure without multiple weak planes
2.2 不同结构面长度与相对距离时采动巷道破坏行为
2.2.1 破坏模式
图5所示为结构面长度l为2 m不同相对距离d时圆形巷道的完整破坏过程。结构面与水平方向夹角设定为30°,侧压力系数为0.45。由图5(a)可以看出:裂纹的起裂往往发生于开挖卸荷末尾段(靠近15 ms 处),这表明岩体在开挖卸荷段就已经受到了损伤与破坏。当t=0.015 1 s时,在巷道围岩周边出现局部的板裂化破坏。这些裂纹主要是由开挖卸荷应力集中引起的。随着卸载的持续进行,巷道周边裂纹(尤其是巷道右侧)进一步得到扩展,破坏程度持续增大。当t达到0.015 8 s 时,3 条结构面内部均出现大量的宏观裂纹,表明结构面之间开始发生相对滑移与破坏。当t=0.02 s时,可以明显观察到大量岩块向巷道内部飞溅弹射,结构面附近岩体得到进一步恶化,属于典型的岩爆破坏现象。一方面,开挖卸荷引起的板裂化破坏使得结构面附近应力与能量集中,在切向集中应力作用下极有可能导致结构面发生剪切错动;另一方面,由于结构面在剪切错动过程中会释放剧烈的能量,又会进一步诱发巷道周边围岩板裂化岩爆。破坏的岩体呈现出不规则状(剪切破坏,结构面滑移错动导致)与板片状(板裂化破坏所致)并存的特性。随着结构面长度的增加(l=4 m和l=8 m时,如图6(a)和7(a)所示),这种相互作用得到进一步加强。

图5 结构面长度l=2 m不同相对距离d时圆形巷道完整破坏过程Fig.5 Entire failure process of tunnel at various relative distances d to excavation boundary when l=2 m
2.2.2 临界相对距离
由图5可以看出:随着相对距离d的增加,模型内部宏观裂纹逐渐减少(尤其对于巷道右侧围岩)。当相对距离d=1.6 m时,巷道周边围岩破坏程度与未含有结构面时的破坏程度基本一致。这表明当d大于或等于该值时,多结构面的存在将不再影响巷道围岩的稳定性。在本文中,将这个距离为临界相对距离,可理解为:当结构面距离巷道足够远时,将不再受到采掘活动的影响。当结构面长度l=4 m时(图6),虽然巷道右侧围岩破坏程度和损伤范围会随着d增加而降低,但临界相对距离相对于d=1.6 m 时已增加至3.1 m。同样,当l=8 m时(图7),临界相对距离增大到5.6 m。这表明,随着结构面长度的增加,巷道围岩的破坏程度持续恶化,因此,其临界相对距离将呈现单调递增趋势。

图6 结构面长度l=4 m不同相对距离d时圆形巷道完整破坏过程Fig.6 Entire failure process of tunnel at various relative distances d to excavation boundary when l=4 m

图7 结构面长度l=8 m不同相对距离d时圆形巷道完整破坏过程Fig.7 Entire failure process of tunnel at various relative distances d to excavation boundary when l=8 m
2.2.3 动能演化规律
图8所示为不同相对距离d和不同结构面长度l时的最大动能分布情况。从图8可以看出:在不同结构面长度下,最大动能均随着d增加以指数形式单调递减趋势。另外,当结构面长度l为2,4和8 m,且所对应的相对距离d分别为1.6,3.1和5.6 m 时,模型内最大动能与未含有结构面时的最大动能相等。这与图5~7中所确定的临界相对距离是一致的。

图8 不同相对距离d和结构面长度l时最大动能分布Fig.8 Maximum kinetic energy distribution influenced by different d values at various l
2.2.4 位移和最大主应力分布
图9和图10所示分别为l=8 m时不同相对距离模型位移向量场和最大主应力分布云图,箭头的大小表示位移幅值。当t=0.014 8 s时,圆形巷道周边的位移分布比较均匀。由于施加了较大的垂直应力,位移指向始终向下。同样,巷道周边最大主应力也呈现对称分布规律。在卸载过程结束后(t=0.015 2 s),巷道两侧围岩开始向巷道中心移动(箭头指向),尤其是位于结构面一侧的岩体。这表明结构面逐渐活化并有向巷道滑移的趋势。当t=0.019 5 s时,可以明显观察到结构面之间的滑移和错动行为。由于结构面在剪切错动过程中释放剧烈的能量,导致板裂化破坏进一步发展,巷道围岩呈现典型的张拉−剪切混合型破坏现象。

图9 l=8 m且d=0.6 m时模型内不同时刻位移向量场和最大主应力分布云图Fig.9 Displacement vector and maximum principal stress contour with d=0.6 m at different times when l=8 m
当相对距离d=3.6 m时(图10(a)),结构面附近的位移向量并没有发生明显的偏移,结构面之间未出现相互滑移和剪切运动。当相对距离d=5.6 m时(图10(b)),巷道周边的位移场和应力场基本整体呈现对称分布(由于岩石材料的各向异性,仍存在一些细小差别)规律。此时,巷道周边破坏程度和范围与未含有结构面时的情况基本一致(图4)。

图10 l=8 m且d=3.6 m和5.6 m时模型内位移向量场和最大主应力分布云图(t=0.019 8 s)Fig.10 Displacement vector and maximum principal stress contour with d=3.6 m and 5.6 m when l=8 m(t=0.019 8 s)
为了分析不同相对距离d时巷道围岩结构面运移特征,沿3条结构面选取了9个监测点,并绘制了位移−时间演化曲线,如图11所示。从图11(a)可见:当d=0.6 m,t=0.020 0 s时,监测点1,2,3的相对位移介于0.30~0.55 m 之间,而其余监测点的相对位移在0.10~0.20 m 之间。可见,此时的巷道破坏程度很大,体现出明显的岩体动力灾害特性。
从图11(b)可见:9个监测点的最大位移始终介于0.04~0.07 m 之间,明显小于d=0.6 m 时的情况。这些监测点的位移主要来源于所施加的初始地应力,并非来自结构面之间的相对滑移和错动。
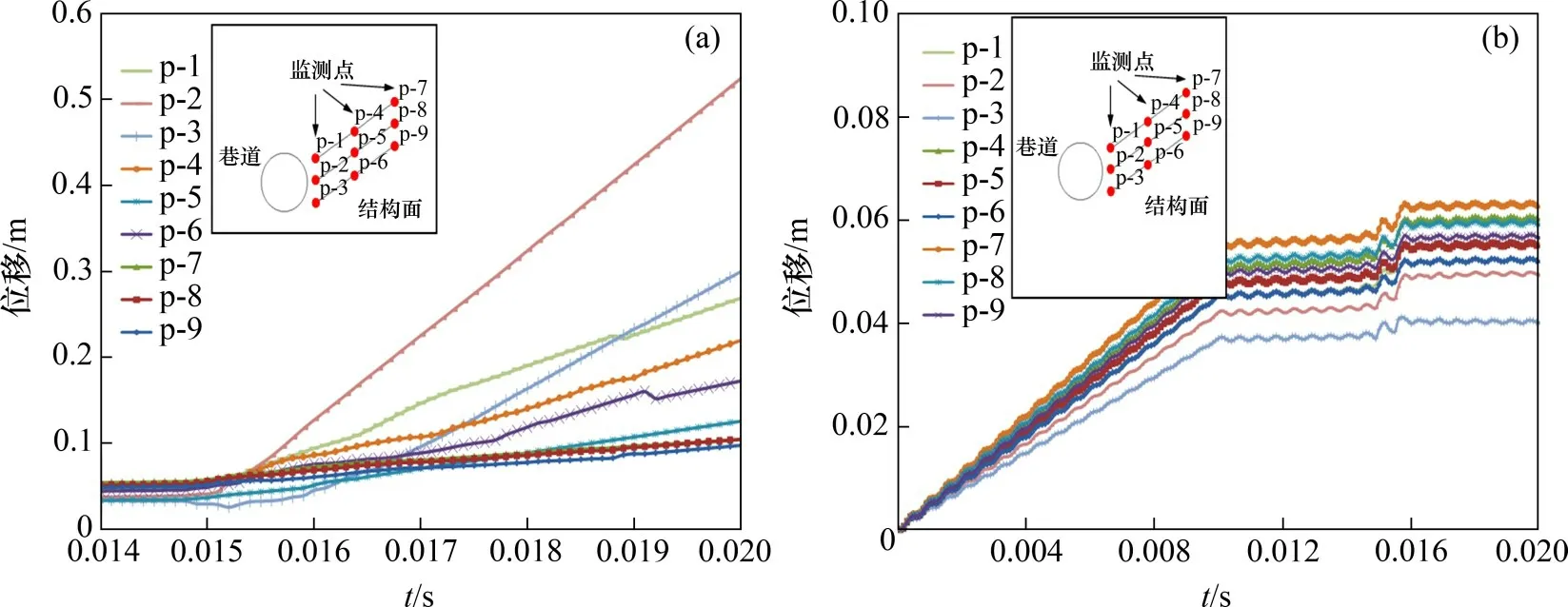
图11 不同相对距离d时沿3条结构面9个监测点位移−时程演化曲线Fig.11 Displacement−time evolution curves for nine selected monitoring points along multiple weak planes at various d
2.3 不同侧压力系数下采动巷道破坏行为
λ=2.25时(垂直应力20 MPa,水平应力45 MPa,此时结构面与最大主应力同侧)巷道围岩有效塑形应变云图如图12所示,其中,结构面倾角θ分别为0°,30°,60°和90°;结构面长度为2 m。
由图12可以看出:巷道周边裂纹已从λ=0.45时(图5和图6)的两帮围岩转移至顶底板围岩。当侧压力系数大于1时,开挖卸荷将引起巷道顶底板围岩应力和应变能的集中。当最大切向应力超过岩石材料单轴抗压强度时,破坏便会发生。值得注意的是,当λ=2.25 时,结构面并没有出现滑移和错动,且巷道右侧结构面附近围岩也没有发生破坏。

图12 λ=2.25时不同结构面倾角θ有效塑形应变云图Fig.12 Effective plastic strain contour at various inclination angles when lateral pressure coefficient λ=2.25
图13所示为不同结构面倾角下模型内动能时程演化曲线。从图13可见:不同结构面倾角θ下,最大动能均为3~4 kJ之间,这与未含有结构面时模型释放最大动能基本相同。由于结构面未参与巷道围岩的破坏行为,巷道周边仅出现板裂化破坏现象。
比较2种不同侧压力系数发现,λ=0.45时,最大动能为9.6 kJ,明显高于λ=2.25 时的最大动能3.7 kJ。可以推断,λ=2.25 时的结构面并没有发生相对滑移和错动,因此也没有能量的释放。此外,当λ=2.25时,动能仅在开挖卸荷段末尾出现波动,没有再出现第二次持续的波动和起伏,其破坏程度和范围都明显小于λ=0.45 时的情况。由于结构面位于应力降低区(即此时最大主应力与结构面位于同一侧),较低的切向应力不足以使结构面发生剪切错动,因此,结构面始终处于稳定状态。此时,板裂化破坏与剪切滑移破坏并不会相互促进和影响,大规模动力灾害现象不易诱发。
3 讨论
从图7可见:相对距离d分别为3.6,4.6和5.6 m 时,多条结构面之间并没有发生破坏,亦未出现滑移和剪切运动。尽管在巷道边界仅观察到板裂化破坏,但是,d为3.6 m和4.6 m时的破坏程度和损伤范围较d=5.6 m 时的更为严重。这表明,即使结构面之间不存在剪切、滑动或错动,深部巷道周围存在的结构面也会潜在地影响巷道围岩的稳定性。
由图10(a)可以看出:圆形巷道周边的最大主应力呈现非对称分布特性,而图10(b)中的最大主应力却呈现对称分布,这说明当相对距离d=3.6 m时,巷道右侧围岩会受到相邻结构面的影响。正是非对称分布的应力场导致右侧巷道围岩出现更多的裂纹和损伤。从这个角度来看,即使结构面之间不发生滑移和错动,结构面的存在也会潜在地促进板裂化破坏(或应变型岩爆)的发展。数值模拟结果表明:以板裂化或应变型岩爆为主的破坏模式可以是开挖卸荷效应和结构面效应的共同作用。因此,在分析深部含结构面采动硬岩巷道破裂特征时,应根据位移场、应力场、动能分布和破坏模式系统地评估其综合响应。
考虑到现场地下工程中很难精确获得多结构面与巷道周边的相对距离(尤其对于多条结构面相互平行时的情况),因此并没有将数值模拟结果与现场实际进行进一步对比分析。尽管如此,本文的数值模拟结果可以较为客观地反映结构面效应与开挖卸荷效应对于深部硬岩巷道破坏的联合作用。
结构面与巷道边界的临界相对距离随结构面长度的增加呈现单调递增趋势。可以推断,对于深部含结构面采动硬岩巷道,其破坏程度是结构面长度和距离的共同作用结果。另外,对于不同初始地应力(侧压力系数)的深部硬岩矿山,结构面与巷道之间的相对位置是至关重要的因素。围岩结构面发生失稳活化的先决条件在于其是否与最大主应力同侧。该结果是对于现场实际工程中可能发生的破坏现象的一系列推断与预测,具有一定的关联性。在今后的研究中,应逐步探索并开展室内试验条件下含结构面采动硬岩巷道的破坏特性研究,并将数值模拟结果与室内试验、现场调研结果进行比较综合分析,以期为深部含结构面采动硬岩巷道的稳定性研究提供理论依据与指导。
4 结论
1)一方面,开挖卸荷引起的板裂化破坏使得结构面附近应力与能量集中,在切向集中应力作用下极有可能导致结构面发生剪切错动;另一方面,由于结构面在剪切错动过程中会释放剧烈的能量,又会进一步诱发巷道周边围岩板裂化(应变型)岩爆。破坏的岩体呈现出不规则状与板片状并存的特性。
2)随着结构面长度的增加,巷道围岩的破坏程度持续恶化。结构面与巷道开挖边界之间的临界相对距离随着结构面长度的增加呈现单调递增趋势。当结构面长度为2,4和8 m 时,临界相对距离分别为1.6,3.1和5.6 m。
3)以板裂化(应变型)岩爆为主的破坏模式可以是开挖卸荷效应和结构面效应的共同作用结果。当小于某一临界相对距离时,即使结构面之间不发生滑移和剪切破坏,结构面的存在也会潜在地促进板裂化破坏(岩爆)的发展。在分析深部含结构面采动硬岩巷道破裂特征时,应根据位移场、应力场、动能分布和破坏模式等系统评估其综合响应。
4)当结构面与最大主应力不同侧时,开挖卸荷以后,结构面层间的错动和滑动总是伴随着动能的持续起伏和波动,呈现出典型的动力灾害特征。当结构面与最大主应力同侧时,结构面之间并不会发生滑移和错动,巷道围岩破坏程度和损伤范围较弱,此时,巷道破坏仅与开挖卸荷效应有关。
