高放废物深地质处置库屏障系统的多场耦合数值分析

赵艺伟，吴志军，王旭宏，侯伟，杨球玉，吕涛，胡大伟，周辉，魏天宇

(1.武汉大学土木建筑工程学院，湖北武汉，430072；2.中国科学院武汉岩土力学研究所岩土力学与工程国家重点试验室，湖北武汉，430071；3.中国核电工程有限公司，北京，100840；4.中国科学院大学，北京，100049)

核能的开发和利用与核技术的飞速发展是20世纪最伟大的成就之一。随着我国核工业的高速发展，大量的核废料，尤其是高放废物(高水平放射性核废物)的产生成为制约核科学技术可持续发展的影响因素之一。高放废物中含有镎、钚、镅、锝等放射性核素，它们具有放射性强、毒性大、半衰期长等特点，无法通过常规的物理、化学、生物等手段去除，只能依赖自身的衰变逐渐去除，然而这个过程十分漫长，甚至可达数万年。安全可靠处置高水平放射性废物已经成为国际社会普遍关注的焦点。

目前，深地质处置是国际上公认的安全处置高放废物可行的处置方式[1]，该方式的实质就是将高放废物置于深度500～1 000 m的稳定的地下岩体中，开挖处置巷道和处置孔，将高放废物放置于耐腐蚀且安全稳定的处置容器，并将处置容器放置于处置孔中，其采用“多重屏障系统”设计思路(见图1)，多重屏障系统分为工程屏障(处置容器、缓冲材料和回填材料)和天然屏障(地下围岩)[2]。处置容器主要用于盛放玻璃固化体(将核废料玻璃固化)，学者一致认为碳钢是制造处置容器的合适材料；缓冲材料通常以砌块的形式包裹于处置容器周围，而处置巷道中填充的材料被称为回填材料，缓冲/回填材料具有阻止地下水进入、限制核素迁移、释放核废料衰变热、保证处置容器的稳定性和耐久性等作用，一般选择封闭性好、高膨胀性、低渗透性、高吸附性、热传导性良好的膨润土(内蒙古高庙子膨润土)作为缓冲/回填材料[3]。围岩是屏障系统的最后一道防线，根据我国地质条件，选择导热性能良好、渗透性较低、力学稳定性良好的花岗岩(甘肃北山花岗岩)作为处置岩层[4]。

图1 屏障系统组成Fig.1 Composition of barrier system

在进行高放废物处置库巷道和处置孔开挖时，围岩由于应力重分布会产生微裂纹，从而造成围岩损伤，围岩的力学参数(强度和弹性模量)、渗透性质(渗透率)和热学参数(热容和热传导系数)都会发生变化。而在高放废物的处置过程中，乏燃料释热是引起屏障系统多场耦合效应的重要原因，乏燃料中放射性元素不断释热导致处置容器温度升高，从而在缓冲/回填材料和围岩中产生温度梯度，随之引起缓冲/回填材料和近场围岩的热变形和热应力。在缓冲/回填材料中，温度梯度是水蒸气传输的动力，而含水量又决定了缓冲/回填材料的释热效率。温度升高使得高放废物处置库屏障系统长期处于多场耦合作用的扰动下，由于对高放废物处置库安全评估的需求，必须进行多场耦合分析。

关于高放废物处置库多场耦合问题，国内外学者做了大量研究。COLLIN 等[5]考虑固体基质体积变形，对非饱和土多场耦合问题进行了研究，建立黏土屏障系统的多场耦合计算模型。蔡国庆等[6]对瑞典CLAB处置库中作为缓冲层的非饱和膨润土进行了热−水−力耦合数值模拟分析。关于缓冲/回填材料的物理化学性质，VECCHIA 等[7−8]对压密膨润土进行了室内试验研究，对其在非等温条件下的吸力效应，以及温度对其渗透系数的影响进行了研究。孙德安等[9−12]对我国高庙子膨润土的各种物理化学性质进行了试验研究。另外，很多学者建立了高放废物处置库围岩的弹塑性损伤模型，侯会明等[13]建立了一个考虑围岩损伤的THM 多场耦合数值模型，对处置库围岩加热试验进行了模拟。陈亮等[14]对甘肃北山花岗岩进行了不同围压下的循环加卸载试验，构建了围岩的弹塑性损伤模型。

总之，国内外学者的研究主要集中在高放废物处置库围岩或者高放废物处置库缓冲/回填材料的多场耦合工作，并取得了一系列的研究成果。国内研究中涉及到的屏障系统的热学参数、力学参数和水力参数大多为常数。在实际工程中，屏障系统的热学、力学和水力参数往往是温度、饱和度、缓冲材料干密度、孔隙水压力、围岩损伤等的函数，耦合过程具有很强的非线性。本文作者基于国内外高放废物处置库屏障系统的多场耦合数值分析，研究高放废物处置库开挖阶段造成的围岩损伤对高放废物处置库关闭阶段渗流场和温度场的影响；建立处置库屏障系统的温度−渗流耦合模型，分析缓冲/回填材料的饱和过程对处置库屏障系统温度场演化的影响和处置库温度变化对缓冲/回填材料饱和度演化的影响。本研究对准确评价高放废物处置库的安全性能以及设置合理设计参数具有一定意义，为我国高放废物处置库的建设提供依据。

1 数值模型的建立

1.1 围岩弹塑性损伤模型

高放废物处置库围岩为花岗岩，岩体具有强脆性特征，理想弹脆性模型在有限元分析中较为常见。然而，当围压越大时，采用理想弹脆性模型的分析结果所产生的误差越大。高放废物处置是将高放废物安装于深度大于500 m的岩体中，高围压是重要特征参数，采用理想弹脆性模型会产生较大误差。因此，本文采用的屈服函数如下[15]：

式中：p1为广义剪应力；p2为平均应力；θ为Lode角；cs为室温下的材料黏聚力系数；Rc为标准化系数，等于室温下岩石的单轴抗压强度；g(θ)为表征π平面屈服曲线随Lode角变化的函数，本文取g(θ)=1；η(γp，d)为硬化函数，与损伤变量d和等效塑性应变γp有关：

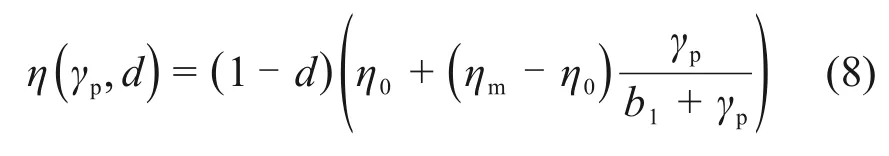
式中：η0为初始屈服值；ηm为硬化准则中的极限值；b1为表征硬化速率的系数；d为损伤变量，在0～1之间；γp为等效塑性应变。

高放废物处置库的开挖损伤区是由开挖引起的应力重分布和机械扰动所形成的，采用损伤变量描述损伤程度，即损伤变量为塑性内变量的指数函数形式。对于深部地质处置库，机械扰动对开挖损伤的影响远小于应力重分布的影响，本文将初始损伤设定为0(即忽略机械扰动的影响)，将损伤极限值设定为1，损伤变量可定义为如下形式[15]：

式中：b2为损伤演化参数；为塑性应变张量。由塑性流动法则可得塑性应变为

式中：dλ为非负标量函数；g为塑性势函数。对于岩石等地质材料，若采用关联流动法则会导致塑性体积膨胀偏大，本文采用的塑性函数为[14]

式中：当η<ηc时，材料塑性体积压缩；当η>ηc时，材料塑性体积膨胀。

围岩的损伤会导致围岩的孔隙率增大，孔隙率与损伤变量之间的关系定义如下[16]：

式中：φ0为围岩的初始孔隙率。

弹塑性应力应变本构关系为：

式中：σeff为有效应力张量；C为弹塑性的切线刚度张量；ε和εp分别为总应变张量和塑性应变张量；σ为总应力张量；b为有效应力系数；I为单位矩阵；ξ为位移张量。

1.2 围岩渗流模型

在高放废物处置库中，围岩基本都处于饱和状态，流体流速缓慢，本文采用达西定理描述围岩的渗流状态：

式中：u为流体流速，k为围岩渗透率，μ为水的动力黏度，随温度变化而变化，根据文献[17]进行插值取值。围岩渗透率随着围岩孔隙率的增大而增大，而由式(13)得知，孔隙率会随着损伤变量的增大而增大。围岩固有渗透率计算公式[18]为：

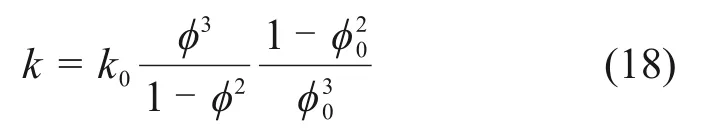
式中：k0为围岩初始孔隙率。

本文采用的渗流本构方程如下[19]：

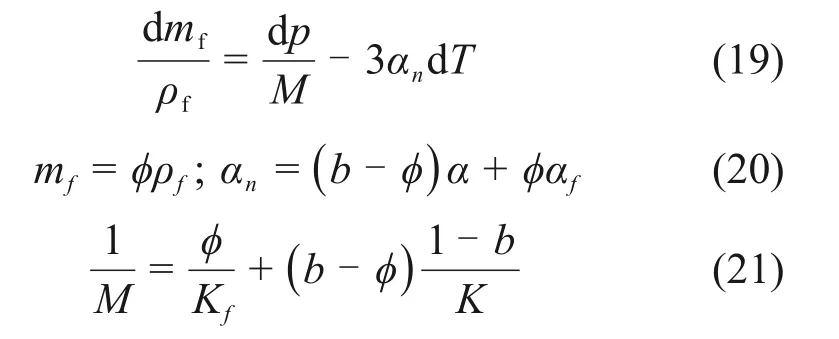
式中：M为Biot 模量；mf，ρf，αf和Kf分别为流体的质量、密度、热膨胀系数和体积模量；p为孔压增量；K为固体基质的体积模量。

同时，在高放废物处置库围岩中，流体满足质量守恒定理：

将式(17)和式(19)代入式(22)后，可得到围岩渗流场的控制方程为

1.3 缓冲/回填材料渗流模型

根据前人的研究结果，选择内蒙古高庙子膨润土作为缓冲/回填材料[3]，膨润土的渗透性较低，饱和时间较长，温度场与渗流场之间存在耦合关系。

非饱和介质渗流控制方程如下[18]：

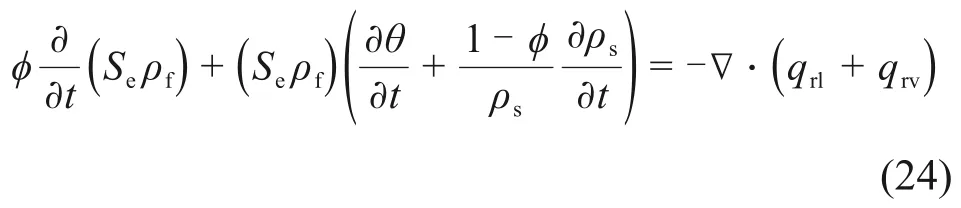
式中：Se为饱和度；ρs为固体基质的密度；qrl和qrv分别为液相水的渗流通量和水蒸气通量。

式(24)左边第一项为储水项，包含VG 持水、孔压储水及热膨胀储水的作用，展开后如式(25)所示：

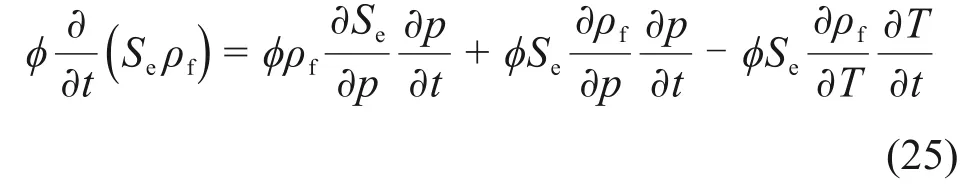
暂不考虑应力场影响，忽略式(24)左边第二项。假定固体颗粒密度仅与温度有关，则式(24)等式左边第三项变形为

假设气压恒定，由Darcy定律和Fick定律可以得到式(24)中的液态水和水蒸气的通量分别为：

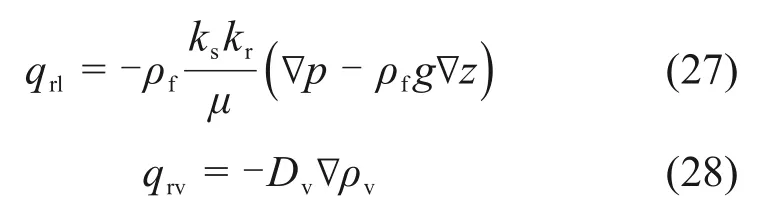
式中：ks为饱和渗透率；kr为相对渗透率，是饱和度Se的函数；z为位置水头；ρv为水蒸气密度，假定气体密度恒定。蒸汽的来源主要包括孔隙间液态水的蒸发以及相邻介质中由于蒸汽分压梯度引起的迁移[20]。水蒸气密度会受到温度梯度和压力梯度影响，但温度梯度变化必然伴随压力梯度的变化，若将压力梯度影响简化处理，可得：

式中：DTv为水蒸气的热扩散系数，可由室内加热试验反推确定[21]。因为DTv是由试验等效得到的，而温度梯度变化必然会引起水的压力梯度变化，所以利用上式计算时已经包含了压力梯度的影响。取值形式如下：

式中：DTvb=1.0×10−11m2/s。

本文可通过孔隙压力p的正负来判断材料当前是否处于饱和状态。计算中使用VAN GENUCHTEN[22]持水曲线模型，模型定义如下，

式中，Hp为孔隙水的压力水头；α与n为VG 模型持水曲线参数；θs为材料参数，数值上等于材料孔隙度；θr为残余水体积分数，取值为0。

针对各类膨润土材料已有的研究表明[23−24]，相同温度下，饱和渗透率与膨润土的干密度的指数线性相关：

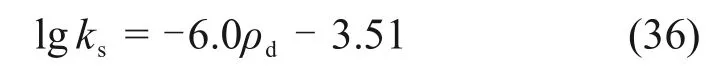
式中，ρd为膨润土材料的干密度。

1.4 孔隙介质热传导模型

利用热动力学理论可以推导出温度场的控制方程为：

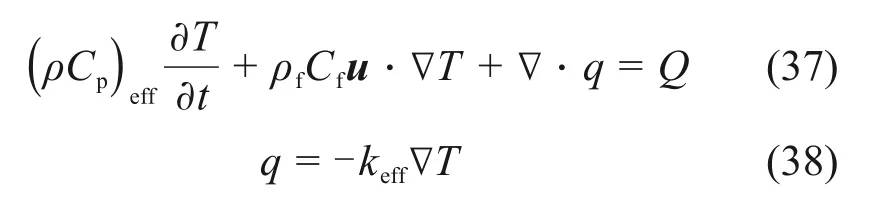
式中：(ρCp)eff为等效体积热容；Cf为流体的质量比热容；u为流体流速；q为单位时间内的热流量；T0为初始温度；keff为等效热传导系数。式(37)左边第一项是累积项，第二项表示流体的对流传热，第三项表示热传导；右边表示热源项，来源于工程实测。

围岩等效热传导系数和等效比热容为

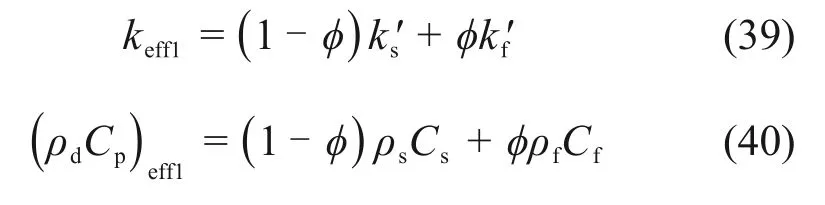
式中：k′s和k′f分别为固体基质和流体的热传导系数；ρs和ρf分别为固体基质和流体的密度；Cs和Cf分别为固体基质和流体的比热容。

同时，缓冲/回填材料的热传导系数和热容均与其他场之间存在有耦合关系[25]，缓冲/回填材料的等效热传导系数和等效比热容分别为：

式中：k1=0.5，k2=0.6，k3=1.07。

由以上分析可知：高放废物处置库开挖阶段造成的围岩损伤主要通过影响围岩孔隙率进而影响围岩的渗透性质和热学参数来影响屏障系统温度场、渗流场；高放废物处置库关闭阶段屏障系统温度场对渗流场的影响主要体现在温度梯度对渗流介质的驱动力和引起的热膨胀，同时，温度变化会导致流体的动力黏度变化影响屏障系统渗透率；渗流场对温度场的影响主要体现在缓冲/回填材料饱和度对材料导热系数和材料比热容等关键热学参数的影响，从而影响温度演化的规律。

2 模型验证

以芬兰POSIVA 2012-48 报告[26]中的有限元分析结果为参照，利用本文建立的数值模型采用与文献[26]相同的相关参数和边界条件进行数值计算，将计算结果与报告中的计算结果作对比分析。乏燃料的释热功率、材料的初始热学参数和初始渗流场参数见表1～3。模型顶底部边界条件设置为定温且定水压，侧面边界设置为绝热且不透水边界，几何模型见图2。选取如图3所示的点A，B，C，D作为分析点，温度和饱和度对比分析分别如图4和图5所示，其中参考值为文献[26]中的计算结果，验证值为本文数值模型的计算结果。从图4和图5可以看出：验证值和参考值基本吻合，说明本文构建的数值模型能正确描述处置库屏障系统的多场耦合过程。

图2 文献[26]中的几何模型Fig.2 Geometric model in Ref.[26]

图3 分析点分布示意图Fig.3 Sketch map of analysis point distribution

图4 点A的温度演化对比Fig.4 Comparison of temperature evolution of point A

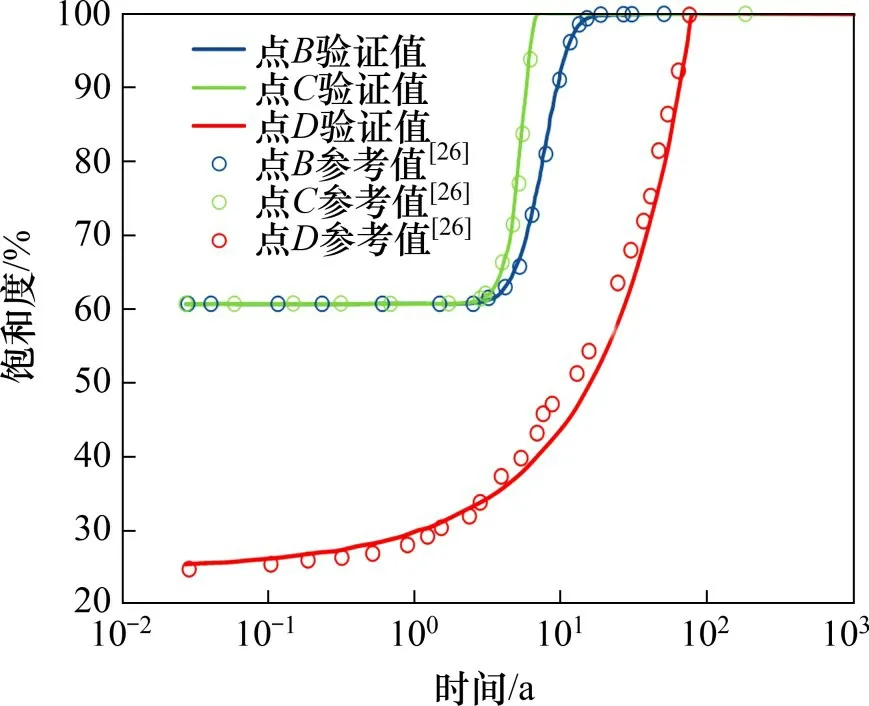
图5 不同分析点的饱和度演化对比Fig.5 Comparison of saturation evolution of different analysis points

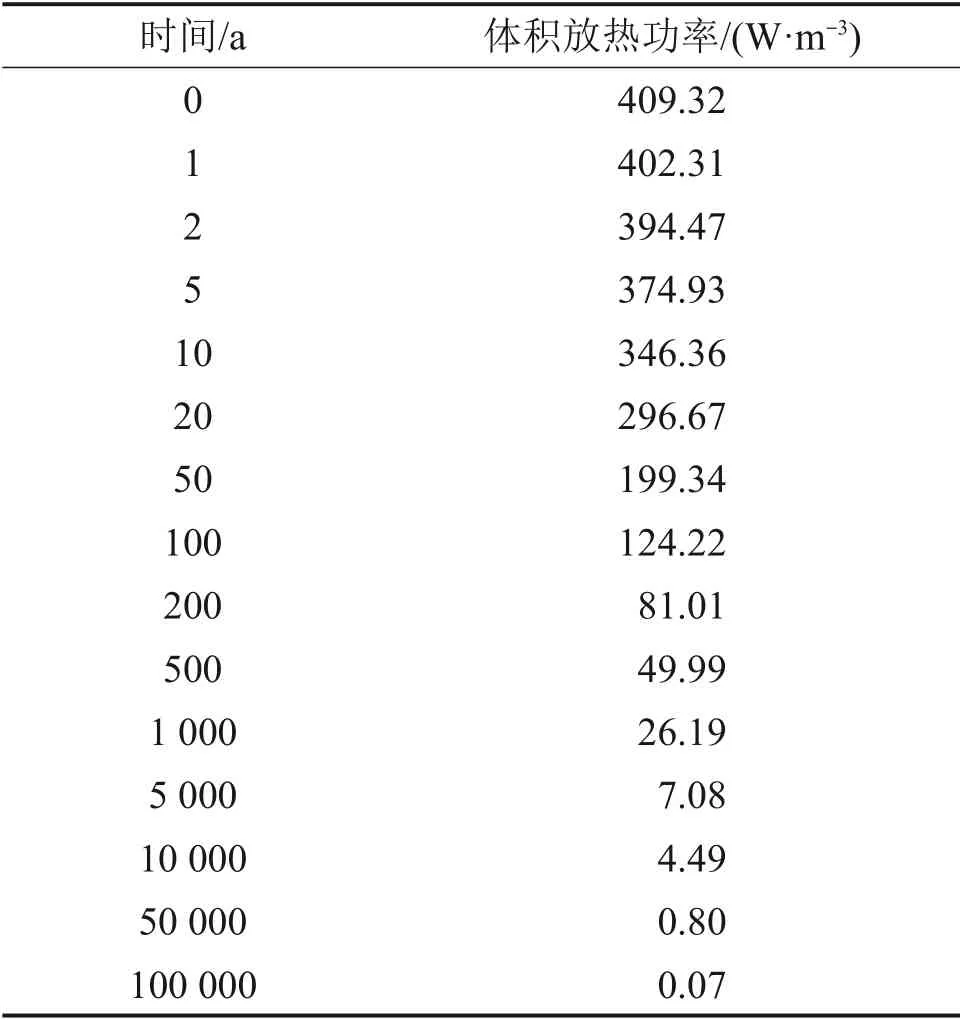
表1 乏燃料等效热功率Table 1 Spent fuel equivalent thermal power

表2 材料初始热学参数Table 2 Initial thermal parameters of material

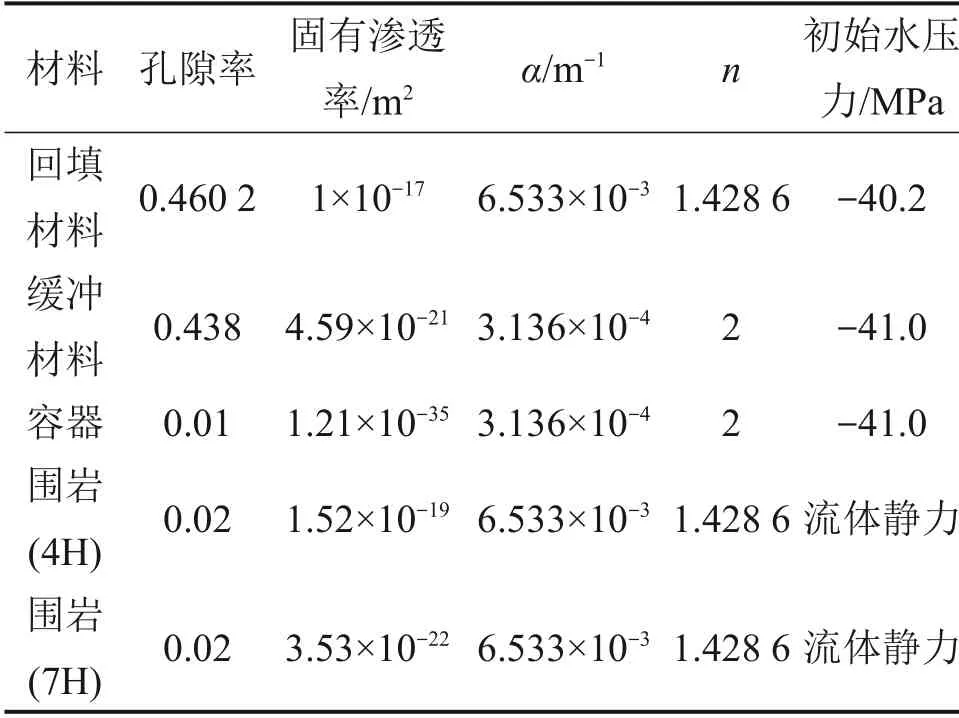
表3 材料的初始参数Table 3 Initial thermal parameters of material

3 有限元数值分析

采用COMSOL Multiphysics 有限元软件(求解偏微分方程为基本仿真模式)[27]分3个步骤进行数值分析，分别为地应力平衡、处置库开挖阶段的围岩损伤分析、处置库关闭阶段屏障系统温度场、渗流场演化规律的分析，图6所示为各步骤的控制方程。

图6 各步骤的控制方程Fig.6 Governing equation of each step

3.1 设计工况和参数确定

设计工况和变化参数如表4所示，其中，Case0-0 为模型采取的基本工况。处置库屏障系统不同介质的其他参数如表5～8所示[20,26,28]。

表4 设计工况和变化参数Table 4 Design conditions and changing parameters

表5 处置容器和玻璃固化体参数[28]Table 5 Parameters of canister and vitrified waste

表6 花岗岩体损伤参数[28]Table 6 Damage parameters of granite bodies

表7 花岗岩体其他参数[26]Table 7 Damage parameters of granite bodies

表8 缓冲/回填材料参数[20]Table 8 Parameters of buffer/backfill materials

3.2 计算模型及其边界条件

参考国内外学者的研究，建立垂直处置的处置库模型。模型长×宽×高为50 m×30 m×18 m，巷道间距为25 m，处置孔间距取为6 m，处置孔直径取1.44 m(处置容器外径为0.74 m，环状宽度取0.35 m)，处置孔深度为4.95 m(处置容器高1.95 m，处置孔上部缓冲材料厚度取2 m，下部厚度1 m)。拱形巷道断面宽度为4 m、直墙高度为3 m、拱顶高度为4.5 m，模型包括2条巷道，6个处置孔。采用有限元软件COMSOL Multiphysics划分网格，如图7所示。

图7 处置孔间距6 m的几何模型Fig.7 Geometrical model when spacing of disposal pit is 6 m

参考文献[26]，模型第一阶段为地应力平衡阶段，模型顶部施加12 MPa 的边界载荷用以模拟围岩上覆岩层质量，底面固定约束，其余各面约束法向位移。第二阶段为高放废物处置库开挖阶段，模型顶部、处置巷道与处置孔临空面设置为自由边界，底面固定约束，其余各面约束法向位移，预应力设置为地应力平衡阶段的计算结果。第三阶段为高放废物处置库关闭阶段屏障系统温度场、渗流场演化规律的分析，参考文献[26]和文献[29]，地表温度为12 ℃，地温梯度按照0.016 2 ℃/m，在深度为500 m 处，岩体的温度为20 ℃，模型顶、底面分别固定水头压力(500 m 水头、530 m 水头)和固定温度(20 ℃)，侧面边界不透水及绝热，假定岩体为饱和介质，缓冲/回填材料的初始含水率为11%。图8所示为玻璃固化体的热输出曲线，实际处置时，玻璃固化体在地面上的暂存时间一般为30 a和50 a，本文按照将玻璃固化体暂存地面30 a计算。

图8 玻璃固化体的释热曲线Fig.8 Heat output from glass waste

4 数值分析结果

依据Case0-0 工况的模拟结果，分别分析高放废物处置库开挖阶段对围岩渗透率在空间分布上造成的影响；分析不同点的饱和度和温度演化规律，阐述高放废物处置库关闭阶段温度梯度对缓冲/回填材料的饱和度演化过程的影响。同时，通过比较分析围岩不同初始渗透率、考虑和不考虑围岩开挖损伤时的模拟结果，分析变化参数对缓冲/回填材料不同特征点的饱和度和温度演化规律的影响，进而阐述缓冲/回填材料饱和度演化进程对温度演化规律造成的影响。

4.1 工况Case0-0结果分析

4.1.1 围岩开挖损伤对围岩渗透率的影响

围岩开挖的损伤变量空间分布如图9所示，损伤变量最大值达到0.038。图10所示为巷道处置孔开挖后围岩渗透率分布图，围岩渗透率分布与损伤变量分布一致，围岩渗透率最大值为2.7×10−16m2。围岩开挖后需要重点关注巷道拱顶与直墙交界处和处置孔底部近场围岩的损伤情况和渗透率变化情况。

图9 围岩开挖后损伤变量分布Fig.9 Distribution of damage variable after surrounding rock excavation

图10 围岩开挖后渗透率分布Fig.10 Distribution of permeability after excavation of surrounding rock

4.1.2 安装处置容器后温度场和渗流场的演化规律

10 个研究点分布如图11所示，点1 位于玻璃固化体中心，点2，3，4分别为处置容器顶面、侧面、底面与缓冲材料的交界点，点5和点6分别位于距处置容器顶面1 m和距处置容器底面0.5 m处，点7为生物回填材料和缓冲材料的交界点，点8和点9 为缓冲材料与围岩的交界点，点10 为距巷道底面2.25 m处回填材料中的点。

图11 研究点分布示意图Fig.11 Sketch map of research points distribution

图12所示为第0.1年、第0.5年、第5年、第20年、第50年、第1 000年时处置库近场的温度分布。处置1 000 a 后，处置库最高温度20.6 ℃，仅比原岩温度高0.6℃。

图12 不同时间的温度分布Fig.12 Temperature distribution at different time

图13所示为不同研究点的温度随时间的演化规律图。从图13可以看出：点1(即玻璃固化体中心)的温度最高，距离玻璃固化体越远其温度越低，在前期，处置库屏障系统各点温度上升很快，在处置库关闭前3年，各点均已达到最高温度，研究点10 达到最高温度的时间最晚，需要2.7 a，达到最高温度后温度缓慢下降，到1 000 a 左右时，各点温度已经趋近于初始温度20°C。根据文献[18]，[26]和[28]等可知，高放处置库安全评估要求处置容器表面最高温度不超过100 ℃，比较处置容器表面研究点2，3和4的温度演化情况可知，研究点3的温度最高，为74.8 ℃，可见：在工况Case0-0下，所模拟的高放废物处置库工程屏障系统是安全的。

图13 不同研究点温度演化Fig.13 Temperature evolution of different research points

图14所示为处置库近场环境在第0.1年、第1年、第2年、第5年、第20年和第24年的饱和度分布。可见：在第2年处置容器附近的缓冲材料基本达到完全饱和，回填材料在处置24 a 后已经达到完全饱和。

图14 不同时间研究点饱和度分布Fig.14 Saturation distribution of point at different time

研究点3，5，6，7，10 的饱和度随时间的演化规律见图15。从图15可以看出，回填材料和缓冲材料中不同研究点的饱和时间不同，研究点3与围岩距离最近，因此达到饱和的时间最早，为0.69 a，研究点5，6，7，10 达到饱和的时间分别为2.10，1.40，5.80和23.90 a。值得一提的是，在处置库关闭初期，缓冲/回填材料饱和度会缓慢下降并降至初始饱和度以下，研究点3的饱和度最低值最小，为46.3%，随后，饱和度才快速上升达到完全饱和(即饱和度为100%)，饱和度的这种演化规律与文献[30]的相似。发生这种现象的原因是，处置库关闭初期温度上升很快，各特征点迅速达到最高温度，温度由内到外增加，短时间内产生了较大的温度梯度，温度梯度驱使水蒸气从高温端迁移到低温端，导致缓冲材料的含水量出现短暂下降，在此期间温度梯度对流体扩散的影响要大于液体压力梯度的影响。随着处置库屏障系统不断升温，流体的动力黏度减小，从而导致缓冲/回填材料和围岩的渗透率增加，加快了屏障系统近场的孔隙水渗透；同时，达到最高温度后，各研究点温度开始缓慢下降，缓冲/回填材料的温度逐渐趋向于均匀，温度梯度减小，使得温度梯度对水蒸气的影响逐渐小于压力梯度对流体扩散的影响，促使缓冲材料的饱和度增加并迅速达到饱和状态。图16和图17所示分别为不同研究点导热系数和比热容的演化规律。因为导热系数和比热容都是饱和度的函数，导热系数与比热容的演化规律与饱和度演化规律相同，导热系数和比热容在材料完全饱和时达到的最大值分别为1.6 W/(m·K)和1 815 J/(kg·K)。

图15 不同研究点饱和度演化Fig.15 Saturation evolution of different points

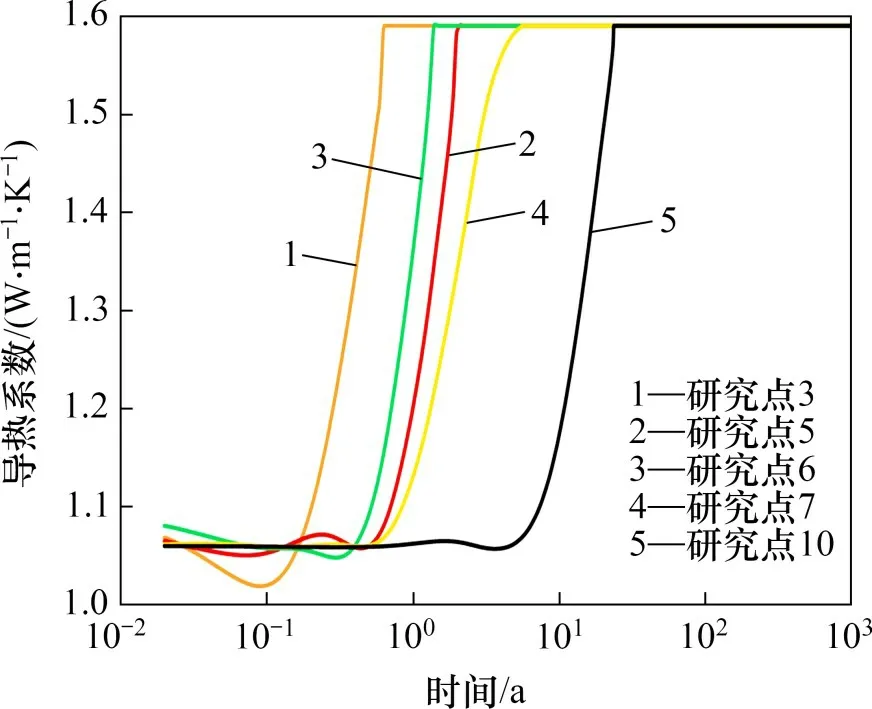
图16 不同研究点导热系数演化Fig.16 Thermal conductivity evolution of different points

图17 不同研究点比热容演化Fig.17 Heat capacity evolution of different points

4.2 围岩初始渗透率对渗流场和温度场的影响

工况Case0-0，Case1-1和Case1-2 中围岩的初始渗透率分别为1×10−17，1×10−15和1×10−19m2，其余条件都相同。图18所示为3 种工况下研究点3，5和10 的饱和度演化情况。从图18可以看出：围岩初始渗透率为1×10−15，1×10−17和1×10−19m2时，研究点3 的饱和时间分别为0.68，0.69和3.40 a；研究点5 的饱和时间分别为2.00，2.10和12.10 a；研究点10的饱和时间分别为23.70，23.90和34.50 a。可见，当围岩初始渗透率减小时，围岩中的孔隙水向缓冲层渗透的速度减缓，导致缓冲/回填材料的饱和时间增加，当围岩的初始渗透率由1×10−15m2降低到1×10−17m2时，研究点3，5和10的饱和时间分别增加0.01，0.10和0.20 a，但是当围岩的初始渗透率由1×10−17m2降低到1×10−19m2时，研究点3，5和10 的饱和时间分别增加2.71，10.00和10.60 a，即当围岩初始渗透率较小时缓冲/回填材料的饱和时间对围岩渗透率的变化更为敏感，这一规律与文献[18]的相似。

图18 不同工况下研究点的饱和度演化Fig.18 Saturation evolution of each research point under different working conditions

图19所示为围岩初始渗透率不同时以及点3的温度演化情况。由图19可知：围岩初始渗透率为1×10−15，1×10−17和1×10−19m2时，研究点3的最高温度分别为74.6，74.8和79.3 ℃，达到最高温度的时间分别为0.37，0.38和0.59 a，3 种工况下研究点3的最高温度均未超过100 ℃，工程屏障系统的安全性良好。同时，当围岩的初始渗透率由1×10−15m2降低到1×10−17m2时，研究点3的最高温度增加了0.2 ℃，达到最高温度的时间推迟了0.01 a；但是当围岩的初始渗透率由1×10−17m2降低到1×10−19m2时，研究点3 的最高温度增加了4.5 ℃，达到最高温度的时间推迟了0.21 a，即当围岩初始渗透率较小时，处置库屏障系统的最高温度和达到最高温度的时间对围岩渗透率的变化更为敏感，这与围岩初始渗透率对缓冲/回填材料饱和时间的影响在定性上是一致的。这是由于缓冲/回填材料中的热传导系数和热容与材料的饱和度相关，当材料饱和度越高其热传导系数和热容也会相应越高，从而更有利于热量向外界扩散，温度会相应较低，即缓冲回填材料的饱和过程会加速处置库屏障系统中热量的传递，有利于处置库屏障系统的安全。

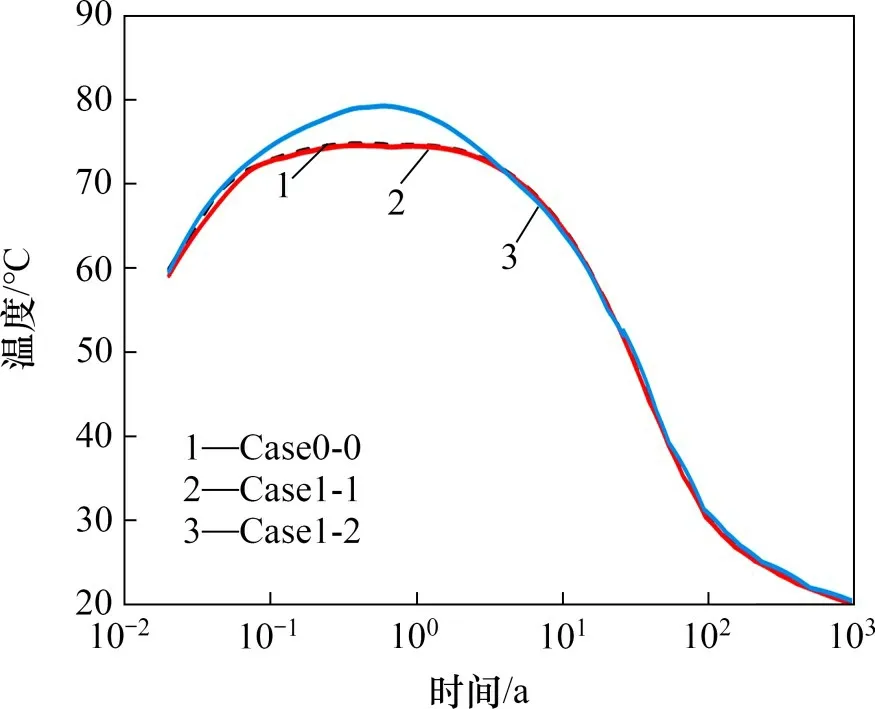
图19 不同工况下研究点3的温度演化Fig.19 Temperature evolution of point 3 under different operating conditions

4.3 围岩损伤对渗流场和温度场的影响

由4.2节可知，当围岩初始渗透率较小时处置库屏障系统的渗流场和温度场的演化对围岩渗透率的变化更为敏感。因此，在较低的围岩初始渗透率下对比分析是否考虑围岩损伤对处置库屏障系统渗流场和温度场演化规律的影响。Case1-2 工况下围岩开挖后渗透率的分布如图20所示。从图20可以看出，其渗透率空间分布与图7相同，但最大渗透率达到2.7×10−18m2。巷道拱顶与直墙交界处的渗透率受到围岩损伤的影响最大，重点分析该水平截线上的特征点的饱和度演化情况，如图21所示，分别选取距离巷道拱顶与直墙左交点为0.1，0.5和1.0 m 的点a，b，c和研究点10 分析围岩损伤对其饱和过程和温度演化的影响。

图20 Case1-2工况围岩开挖后渗透率分布Fig.20 Permeability distribution after excavation of surrounding rock in Case1-2

图21 考虑围岩损伤的研究点分布示意图Fig.21 Distribution of research points considering surrounding rock damage

图22所示为考虑围岩损伤(Case1-2)与不考虑围岩损伤(Case2-1)时研究点a，b，c和10的饱和度演化情况。从图22可以看出，在Case1-2 工况下，研究点a，b，c和10 的饱和时间分别为16.3，26.0，31.4和34.5 a；在Case2-1工况下，研究点a，b，c和10 的饱和时间分别为18.9，27.5，32.4和35.2 a。与Case2-1 工况相比，Case1-2 工况下，研究点a，b，c和10的饱和时间分别少2.6，1.5，1.0和0.7 a。距离拱顶与直墙交界处越远，围岩损伤的影响越小。

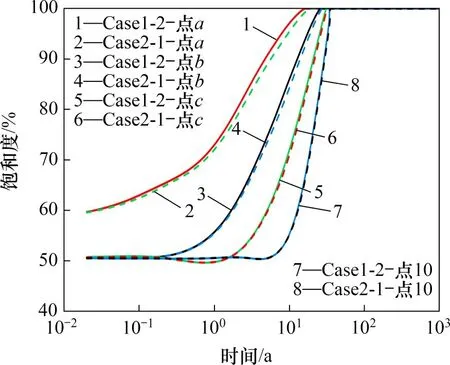
图22 不同工况下研究点的饱和度演化Fig.22 Saturation evolution of each research point under different working conditions

图23所示为考虑围岩损伤(Case1-2)与不考虑围岩损伤(Case2-1)时研究点3的温度演化情况。由图22可知：在Case1-2和Case2-1工况下，研究点3的最高温度分别为79.3 ℃和80.0 ℃，达到最高温度的时间分别为0.59 a和0.60 a，2种工况下处置容器的表面最高温度均未超过100 ℃，可以保证处置库屏障系统的安全。不考虑围岩损伤时，点3最高温度增大0.7 ℃，达到最高温度的时间增加0.01 a。由此可见，考虑围岩损伤会使得围岩损伤区的渗透率增加，从而使得缓冲层饱和时间减少，加快热量向外传递。

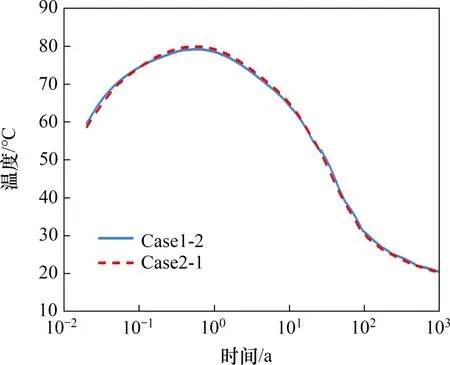
图23 不同工况下研究点3的温度演化Fig.23 Temperature evolution of data point 3 under different operating conditions

5 结论

1)当围岩初始渗透率为1×10−17m2且考虑处置库开挖阶段对围岩造成的开挖损伤时，处置库屏障系统各研究点在处置库关闭前3年迅速达到最高温度，处置容器表面能达到的最高温度为74.8 ℃；因处置库关闭前期温度上升很快，使得处置库屏障系统在近处置容器端产生了较大的温度梯度，驱使水蒸气从高温端扩散至低温端，使得缓冲/回填材料中的各研究点在处置库关闭前期饱和度降低至初始饱和度(50.5%)以下，处置容器侧面的特征点(点3)饱和度下降最多，达到46.3%；随着处置库屏障系统温度变化趋势逐渐趋于平缓，屏障系统中的温度梯度变小，缓冲/回填材料中各点也逐渐趋于饱和，在处置库关闭23.90 a 后缓冲/回填材料中各研究点均处于饱和状态。

2)当围岩渗透率变小时，处置库屏障系统各研究点的饱和时间延迟，处置容器表面的最高温度增大，但当围岩初始渗透率较小时，处置库屏障系统的渗流场和温度场的演化对围岩渗透率的变化更为敏感：当围岩的初始渗透率由1×10−15m2降低到1×10−17m2时，各研究点饱和时间相差最大值为0.20 a，处置容器表面的最高温度增加了0.2 ℃，达到最高温度的时间推迟了0.01 a；当围岩的初始渗透率由1×10−17m2降低到1×10−19m2时，各研究点饱和时间相差最大值为10.6 a，处置容器表面的最高温度增加了4.5 ℃，达到最高温度的时间推迟了0.21 a。可见，考虑缓冲/回填材料的饱和过程会加快屏障系统的热量传递，可以更精确的评估屏障系统的安全性。

3)与考虑处置库开挖阶段围岩开挖损伤时相比，不考虑围岩开挖损伤时，缓冲/回填材料的饱和时间更长，对靠近围岩损伤区的缓冲/回填材料的饱和度演化更为明显，各研究点中饱和时间相差最大值达到了2.6 a。同时，处置容器表面的最高温度也提高了0.7 ℃，从而使得对处置库屏障系统安全性的评估更为保守。在本文特定的算例条件下，处置容器表面的最高温度均未超过100 ℃，表明模拟的高放废物处置库屏障系统是安全的。