等质量圆形基础与风电空心锥形基础承载特性

2021-09-26李大勇胡靖彦张雨坤

科学技术与工程 2021年25期

李大勇，胡靖彦，张雨坤*

(1.山东科技大学山东省土木工程防灾减灾重点实验室，青岛 266590；2.山东科技大学土木工程与建筑学院，青岛 266590)

当前全球正面临生态环境恶化与化石能源枯竭等压力，对可再生能源的研究和发展成为热点。风电作为一种环保洁净的绿色能源，得到了许多国家的重视。据估算，到2050年全球风电累计装机容量将达3 203 GW[1]。中国气象局风能太阳能资源中心指出中国陆地离地50、70和100 m高度层上的风能资源技术开发量分别为2 000、2 600和3 400 GW[2]。因此，风电具有良好的发展前景。

重力式扩展基础是目前应用于陆地风电最广泛的基础形式，许多学者从模型试验、数值分析、理论方法等方面对其承载性能做了充分研究。Govoni等[3]求得了密实砂土中圆形基础水平承载力的计算公式并讨论了砂土密实度和基础尺寸对水平承载力的影响。Hossain等[4]分析了极端荷载作用下圆形基础的破坏机理，比较了多种荷载条件下的水平承载力、基础周围土体变形规律及范围。Bienen等[5]采用数值模拟的方法，研究了圆形基础在砂土中的承载性能和基础周围土体变形规律，讨论了相对密实度对水平承载性能的影响。Mohamed等[6]利用工程实例数据，分析了竖向荷载对圆形基础水平承载力与变形的影响，研究了圆形基础的承载机理。Zidan等[7]采用室内试验和数值模拟相结合的方式对圆形基础在竖向荷载作用下的承载性能进行了研究，并考虑了土层加固对承载力和地基沉降的影响。Hartwig等[8]采用全尺寸模型试验，验证了用于描述重力式基础加载的力学行为的计算模型。梅毕祥等[9]使用极限平衡方法，对圆形基础在主要破坏模式下的极限荷载进行了理论推导，开展了基础截面尺寸等参量对承载特性的影响分析。

然而圆形重力式基础与地基为刚性连接，缺乏柔性，导致其在极端条件下可能发生整体倾覆或塔架折断等工程事故。此外，通过工程调研，发现基础基坑开挖将产生大量渣土，通常做法为就地堆放，影响基础稳定性，同时破坏周围植被环境。为了克服上述不足并提高基础承载力，李大勇等[10]基于海洋平台Spudcan基础的理念提出了一种新型的陆地风电塔架基础——山区风电钢筋混凝土空心锥形基础(简称空心锥形基础)。相较于传统重力式圆形基础，空心锥形基础增加了与土体的接触面积，有效提高了基础的承载力和稳定性。同时将开挖的废弃渣土作为基础的一部分，降低了建造成本并减小渣土对环境的破坏。

针对空心锥形基础，已开展了一系列模型试验和数值模拟研究。Li等[11]通过模型试验和数值模拟证明了基础径高比相同的条件下，空心锥形基础的水平承载力较圆形基础增加了约33.5%，且累计旋转减少了近50%。此外混凝土用量仅为圆形基础的1/5。邢国起等[12]采用有限元数值方法研究了空心锥形基础的承载特性和破坏机理，比较不同径高比下的基础承载力，得到了极限状态下锥形基础的破坏机理。李大勇等[13]通过开展模型试验，研究了加载高度、加载速率及基础尺寸等因素对锥形基础水平承载特性的影响。研究表明：加载速率对锥形基础水平承载性能影响较小，基础径高比和底板尺寸是影响极限承载力的主要因素。

现研究钢筋混凝土质量相等条件下锥形基础在砂土中承载特性，采用有限元软件PLAXIS3D模拟不同尺寸锥形基础在外荷载分量单独作时的承载特性，以得到能够实现基础最优性能的尺寸设置，并使其适应更大装机容量的风电机组的基础需要；分析地基土的影响范围及变形规律；讨论试验中比尺效应对基础极限承载力的影响。

1 有限元建模

1.1 模型尺寸与土体参数

基础模型参考青岛某山区风电塔架基础尺寸，即基础高度H为3 600 mm，直径D为18 000 mm的钢筋混凝土圆形基础。经等钢筋混凝土质量换算得到两组空心锥形基础的详细尺寸。回填渣土高度与基础高度，基础侧壁、顶(底)板厚度与基础高度的比值一致，回填渣土体积占总体积比值相同，且符合优选的钢筋混凝土壁厚设计方案[10]。不同工况基础编号及尺寸如表1所示，基础剖面如图1所示。

对圆形基础与锥形基础，采用十节点实体单元建立有限元模型，如图2所示。为消除边界效应影响，水平方向取10倍圆形基础直径、深度方向取10倍圆形基础高度范围内土体作为计算区域。为更有效计算外荷载分量单独作用时的基础承载力，采用位移控制式加载方式，不考虑偏心水平荷载的作用，逐步施加位移，荷载作用在基础顶面中心处。

D、H分别为圆形基础的直径和高度；D1、D2分别为空心锥形基础Ⅱ的顶板外径和顶板内径；D3、D4分别为空心锥形基础Ⅲ的顶板外径和顶板内径；D5、D6分别为空心锥形基础Ⅲ的底板内径和底板外径；H1、H3分别为空心锥形基础Ⅱ、Ⅲ的高度；H2、H4分别为空心锥形基础Ⅱ、Ⅲ的回填渣土层高度图1 模型基础剖面图Fig.1 Foundations profiles of models

西北地区是中国重要的风电基地，风场地基土主要为砂土。因此地基土选用砂土，土体参数取自文献[14]，其中黏聚力c=0.1 kPa，内摩擦角φ=34°。采用Mohr-Coulomb模型模拟岩土本构关系，剪胀角ψ=φ/2，泊松比μ=0.3。砂土的变形模量E0=10 MPa，采用变形模量E0代替弹性模量E。基础与土体间设置接触面，摩擦因数为0.45。钢筋混凝土基础选用线弹性模型，弹性模量和泊松比分别取300 GPa和0.2。

图2 基础有限元模型Fig.2 FEM models of foundations

1.2 模型合理性验证

为验证数值模拟准确性，选取模型尺寸与实际工况尺寸之比为1∶70的圆形基础与相应的钢筋混凝土质量相等的空心锥形基础进行水平加载，将模型试验与数值模拟结果对比，如图3所示，两种类型的基础在相同加载条件下，无量纲化数据结果吻合较好[14]。

无量纲水平载荷公式为

P=H/(2πγR3)

(1)

无量纲水平位移公式为

z=u/D

(2)

式中：H为基础受到的水平荷载；R为圆形基础半径；γ为砂土重度；u为基础水平方向总位移；D为圆形基础直径。

在相同的材料和尺寸条件下，通过选用的数值模拟方法，对邢国起等[12]利用基础工程实例数据开展的数值模拟进行验证。图4为相应的关系曲线。竖向承载力误差在14%之内，计算结果可靠。

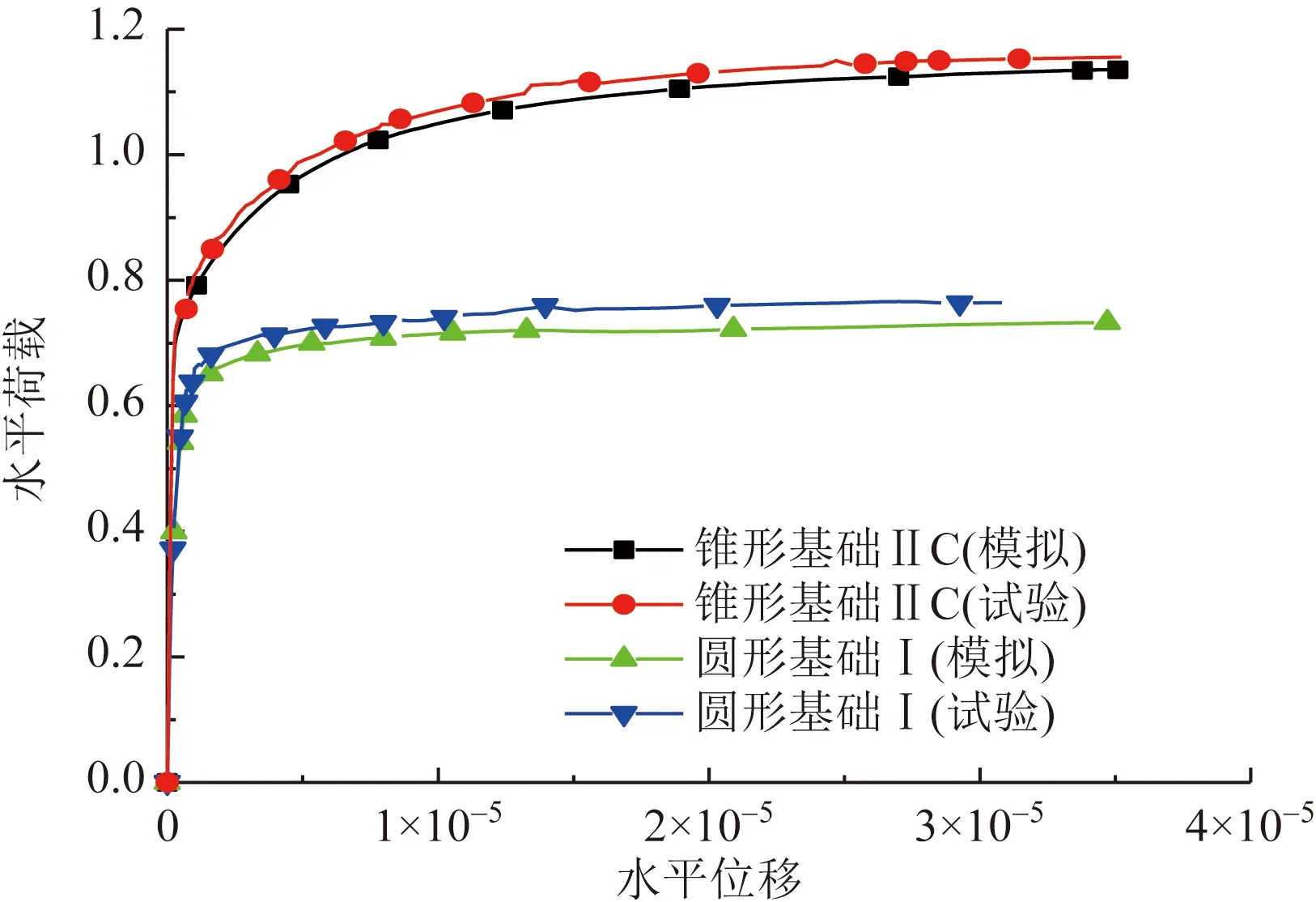
图3 数值模拟与试验结果对比Fig.3 Results between FEM and experiment

表1 基础模型尺寸Table 1 Dimensions of the foundation models

图4 基础竖向荷载与沉降量有限元结果对比Fig.4 Comparison of FEM results

2 计算结果分析

2.1 基础水平承载力及土体变形分析

图5为圆形基础和空心锥形基础的水平荷载-位移关系曲线。计算结果表明，空心锥形基础的极限水平承载力较圆形基础有很大提高，最大提高456%，平均提高247%，具体增长比例如表2所示。

同一荷载等级下，锥形基础的水平位移较圆形基础大幅减少，以图5(a)中水平荷载为20 000 kN为例，其最大减小幅度为90.2%。比较不同尺寸设置的空心锥形基础，其荷载-位移关系曲线的趋势基本一致。在钢筋混凝土质量相等条件下，随着径高比的减小，其水平承载力呈增加趋势，且增长速度逐渐加大。同时，未设置底板的空心锥形基础的水平极限承载力较设置底板的空心锥形基础均有一定程度的提升。

荷载作用下圆形基础的最大隆起量较小，而由图6曲线可知空心锥形基础周围土体的隆起量在0.009～0.047倍圆形基础高度间。

表2 水平极限承载力增长比Table 2 Improving ration of ultimate bearing capacity

图5 水平荷载-位移关系曲线Fig.5 Horizontal loading-displacement curves

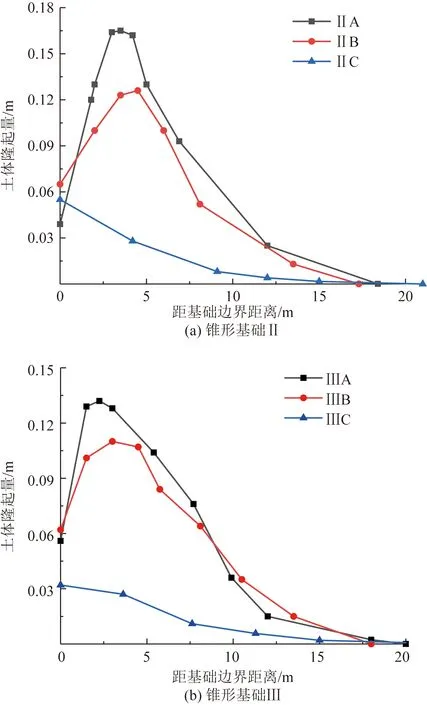
图6 水平荷载下基础前侧土体隆起Fig.6 Soil heave in front of foundation under horizontal loading

且土体隆起量随基础径高比的增加而减小。未设置底板的锥形基础土体隆起量均大于设置底板的锥形基础，调动了更多土体。

为了更好地研究荷载作用下土体的破坏机理，图7体现了不同基础在水平荷载作用下引起的基础周围土体变形，通过对位移云图的比较发现，空心锥形基础在水平加载极限状态发生了土体的局部剪切破坏，而圆形基础表现为基础的倾覆。同时，圆形基础在水平方向上对土体的影响范围约为其直径的0.47倍，竖直方向的影响范围约为其高度的1.7倍。随着空心锥形基础径高比的减小，水平方向的影响范围为0.58～0.94倍圆形基础直径，竖直方向为圆形基础高度的1.6～3.1倍。因此，不同尺寸的基础均能调动更多土体并产生更大的土体抗力；且基础周围受影响的土体范围在水平和竖直方向均明显扩大。综上，在钢筋混凝土质量相等条件下降低基础径高比，能有效提高其水平承载性能。

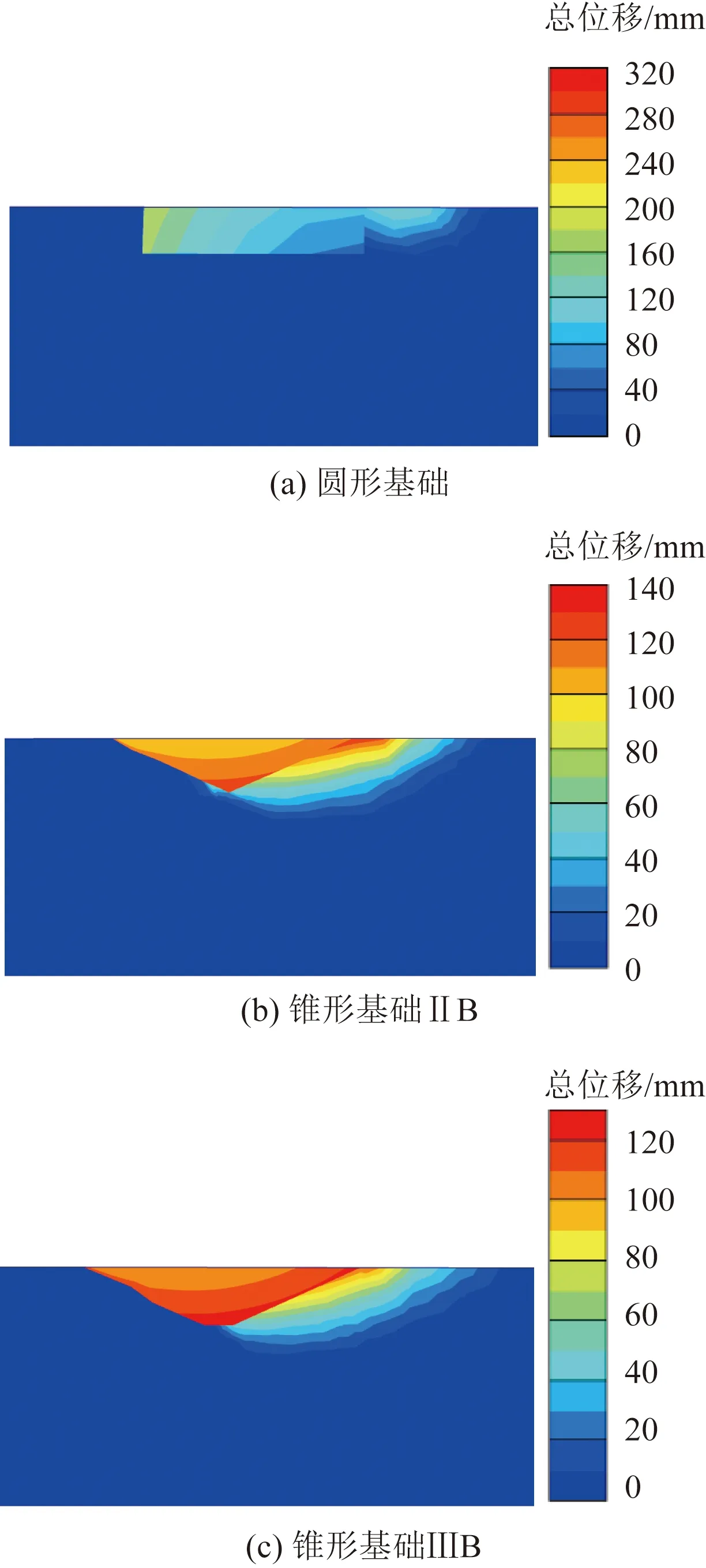
图7 水平荷载作用下基础位移云图Fig.7 Soil deformation under horizontal load

2.2 基础竖向承载力及土体变形分析

图8为圆形基础与空心锥形基础的竖向荷载-沉降量关系曲线。由图8可知：不同尺寸的基础荷载-沉降量曲线趋势基本一致。本例中空心锥形基础竖向极限承载力存在小于圆形基础的情况，因而存在优选的尺寸设置使得基础更好地抵抗竖向荷载。同时，随着基础径高比的增大，空心锥形基础竖向极限承载力不断增加，变化范围在0.9×106～4.2×106kN。

由于锥形基础受竖向荷载作用时，基础侧面和底面承担了大部分的抗力，则表3为极限状态下锥形基础随其与土体接触面积变化引起的承载力变化比，由表可知：随着锥形基础与土体接触面积的增加，其竖向承载力有所提高，以基础ⅡC为例，极限承载力增幅为35.5%。说明锥形基础与土体接触面积的大小在其承担竖向荷载时发挥了显著作用，提高基础径高比能有效提高其承载性能。

图8 竖向荷载-沉降量关系曲线Fig.8 Vertical loading-settlement curves

表3 基础-土体接触面积增加比与竖向极限承载力变化比Table 3 Improving ration of foundation-soil contact area and changing ration of ultimate bearing capacity

在竖向荷载作用下，两种基础趋向极限状态时有着不同的破坏模式。重力式圆形基础表现为基础周边下方持力层土体的局部剪切破坏，锥形基础为基础中心下方及周边下方持力层土体的局部剪切破坏[12]。即圆形基础下方土体在极限状态时等效塑性应变值较小，土体不易发生破坏，而锥形基础由于其结构原因，其中心下方土体等效塑性应变值较大，在一定的尺寸条件下抵抗竖向荷载的能力存在逊于圆形基础的情况。图9为竖向荷载作用极限状态下基础的位移云图，可知：空心锥形基础在极限状态时周围土体的变形趋势与圆形基础基本一致。且随着锥形基础径高比的增加，基础周围土体的隆起范围逐渐扩大，由1.8倍圆形基础直径增至2.6倍，竖直方向上的影响范围也由4.4倍圆形基础高度扩大到5.6倍，由此逐渐产生更大的土体抗力，提高竖向承载性能。

图9 竖向荷载作用下基础位移云图Fig.9 Foundation deformation under vertical load

2.3 基础弯矩承载力及土体变形分析

图10为圆形基础与空心锥形基础的弯矩-转角关系曲线。比较各基础的弯矩极限承载力，发现空心锥形基础的极限承载力随着基础径高比的增加而提高。且不同尺寸的锥形基础抵抗弯矩的能力均较圆形基础显著提高，如表4所示，本例中最大提高793%。

图10 基础弯矩-转角关系曲线Fig.10 Moment loading-rotation curves

表4 弯矩极限承载力增长比Table 4 Improving ration of ultimate bearing capacity

同时，未设置底板的锥形基础Ⅱ较设置底板的锥形基础Ⅲ拥有更强的抵抗弯矩作用的能力。由图11可知，锥形基础前侧土体的隆起量在0.001 4～0.009 2倍圆形基础高度间，隆起高度随基础径高比的增加而减小，隆起范围则反之。

为研究弯矩对基础周围土体变形的影响，由图12可知，两种基础在荷载作用下，土体的变形规律略有差异，但都表现为基础的倾覆与基础前侧土体的隆起。圆形基础引起的土体变形较小，锥形基础在荷载作用下，基础周围土体隆起范围为0.6～0.82倍圆形基础直径；深度方向对土体的影响范围为1.2～2.92倍圆形基础高度。即随基础径高比的增大，调动了更多土体产生抗力。

图11 弯矩荷载下基础前侧土体隆起Fig.11 Soil heave in front of foundation under loading

图12 弯矩作用下基础位移云图Fig.12 Soil deformation under moment load

3 比尺效应对空心锥形基础承载特性的影响

在试验研究中，基础模型的比尺效应对试验结果有一定的影响。为研究比尺效应对空心锥形基础水平、竖向和弯矩承载力的影响规律，采用数值模拟的方法研究不同比尺设置的基础的承载性能，为空心锥形基础在实际工程中的应用和模型试验研究提供参考。分别设置基础原尺寸与模型尺寸比为1∶10、1∶20、1∶50、1∶70、1∶100及1∶200这6种比尺的模型，原型基础采用ⅡC工况。为了更直观地体现比尺效应对基础极限承载力的影响，将数值模拟结果进行无量纲化处理，其中水平荷载、竖向荷载及弯矩的无量纲处理方式为：H/2πγR3、V/2πγR3和M/2πγR4，其中H、V和M分别为基础受到的水平荷载、竖向荷载和弯矩，R为圆形基础半径，γ为砂土重度。水平位移、竖向位移和转角无量纲化方法为：u/D、v/D和2Rθ/D[14]，其中，u、v分别为水平方向和竖直方向上基础的总位移，θ为弯矩作用下基础旋转产生的角度。

3.1 比尺效应对水平极限承载力的影响

在不同比尺的空心锥形基础ⅡC模型顶板中心处施加水平荷载至极限状态，得到由图13所示的无量纲化水平荷载-位移曲线以及随比尺效应的改变而引起的基础水平极限承载力的变化规律曲线(图14)。

在本次研究给定的范围内，空心锥形基础ⅡC的无量纲化水平极限承载力随着有限元模型比尺的缩小而呈现出增大的趋势。当比尺大于1∶70时，基础的无量纲化水平极限承载力保持在相对稳定状态，较全尺寸模型的无量纲水平极限承载力值0.97增幅在20%之内；而当比尺小于1∶70时，比尺效应引起的承载力增幅更为明显，与全尺寸模拟的结果产生较大偏差。模型比尺与水平极限承载力曲线的拟合方程为

图13 无量纲化水平荷载-位移曲线Fig.13 Normalized load-displacement curve

图14 比尺-水平极限承载力曲线Fig.14 Scale-horizontal ultimate bearing capacity curve

HULT=1.5-15.4S+119S2

(3)

式(3)中：HULT为水平极限承载力；S为原型基础尺寸与模型基础尺寸之比。

3.2 比尺效应对竖向极限承载力的影响

在不同比尺的空心锥形基础ⅡC顶板中心处施加竖向荷载至极限状态，图15为无量纲化竖向荷载-沉降量曲线，图16为无量纲化比尺-竖向极限承载力曲线。由图16可知，随着有限元模型比尺的逐渐减小，基础的无量纲化竖向极限承载力呈现出稳定的增加趋势。模型比尺与竖向极限承载力曲线的拟合方程为

图15 无量纲化竖向荷载-沉降曲线Fig.15 Normalized vertical load-settlement curve

图16 比尺-竖向极限承载力曲线Fig.16 Scale-vertical ultimate bearing capacity curve

VULT=178.8-2 878.2S+18 948.6S2

(4)

相较于全尺寸模型模拟计算的结果，当模型比尺仅为1∶10时，其无量纲化竖向极限承载力便增大了48%；而当模型比尺达到1∶100时，极限承载力的增幅达到267.3%。说明比尺效应对空心锥形基础竖向极限承载力的影响极大，且过小的有限元模型比尺设置得出的结果无法为基础的竖向承载性能提供较为准确有效的指导和参考。

3.3 比尺效应对弯矩极限承载力的影响

在不同比尺的空心锥形基础ⅡC顶板中心处施加弯矩至极限状态，得到图17所示的无量纲化弯矩-转角关系曲线，并同时得到图18所示的比尺变化与空心锥形基础极限弯矩承载力的变化关系曲线。由图可知比尺效应对空心锥形基础弯矩极限承载力的影响有限，基础的无量纲化承载力稳定在值2.3左右，且比尺大于1∶100的基础模型的极限承载力仅较全尺寸模型计算结果平均产生9%的增幅。