恒扭矩工具组合式非标碟簧试验与数值分析
2021-09-26温晓松柳贡慧郭雪利
温晓松,柳贡慧*,李 军,郭雪利
(1.中国石油大学(北京)石油与天然气工程学院,北京 102249;2.中国石油集团工程技术研究院有限公司,北京 102206)
常规聚晶金刚石复合片(polycrystalline diamond compact,PDC)钻头在钻遇复杂地层及软硬交错地层时,往往都会遇到扭矩大范围波动的问题。测量数据显示,大部分井段扭矩波动的区间为3~20 kN·m,部分井段的峰值扭矩达到53.3 kN·m。扭矩波动容易引起钻头黏滑失速与钻柱扭振,降低机械钻速,严重时造成钻具损坏及测量工具失效[1-3]。恒扭矩工具拥有的减振、过载保护、稳定转速等特点能有效解决现有钻井过程中扭矩严重波动的问题,减少钻头黏滑失速现象,从而提高钻井速度,其在长庆、塔河、胜利等油田的现场运用中得到同行的一致认可[4-6]。碟形弹簧(简称碟簧)作为该类工具中重要的储能与释能结构,很大程度上决定了工具的性能。作为一种承载能力强、空间体积利用率高、具有变刚度非线性特性的新型弹簧,碟簧被广泛应用于机械、航空、建筑等领域。
中外针对碟簧的研究最早起始于单片碟簧,而组合式碟簧受制于单片碟簧的力学性能、组合形式等多方面的影响,仅在建筑、机械隔振等领域有部分研究。Ozaki等[7]采用数值与试验方法研究摩擦边界对组合式碟簧静态力学性能的影响,并基于能量守恒与摩擦定律,提出一种新的简化方法预测在不同摩擦状态下的载荷-位移曲线。Nicholas等[8]对带方形边缘的单片碟簧建立了一种新的力学模型,该模型将非对称摩擦条件施加在方形边缘上,可准确预测4种不同摩擦状态下的载荷-位移关系,准静态试验结果也支持该模型的有效性。Chaturvedia等[9]考虑几何非线性因素,建立了单片阶梯形碟簧载荷-位移计算模型,并利用有限元法(finite element method,FEM)对模型计算结果进行验证。惠安民等[10]建立了考虑边界摩擦条件下对合碟簧组的刚度与动力学模型,并对其振动特性进行分析计算。王维等[11]对由复合组合形式的碟簧组成的隔震装置建立了一种原点指向恢复力模型,并对该装置进行静载与动载试验,分析了预压量、位移幅值、加载频率等对装置等效刚度及等效阻尼比的影响。徐龙河等[12]通过试验对比分析了内置组合式碟簧的自复位钢筋混凝土剪力墙与普通混凝土剪力墙的区别,结果表明组合式碟簧装置更有利于减小墙体在地震中的损伤和残余变形。韩强等[13]提出一种内嵌组合式碟簧的自复位防屈曲支撑,该支撑通过控制碟簧组的预压力和组合形式得到工程所需的滞回特性曲线。同时对三种不同工况的支撑开展静态试验与对比分析,并从理论上建立了恢复力模型,模型计算值与试验结果吻合较好。张少军等[14]基于试验与数值模拟,对C系列碟簧及非标开槽碟簧的力学性能进行系统研究,分析了不同开槽位置和开槽方式下碟簧的载荷-位移曲线及刚度曲线。邢佶慧等[15]对B系列碟簧组成的不同组合式碟簧进行开展静载与动载试验,研究表明随加载速率的增大,碟簧极限载荷有增大趋势,并给出了用于数值仿真计算的摩擦因数等效值。郭斌等[16]对单片及不同组合状态下的碟簧进行静态及动态阻尼试验,研究表明产生阻尼的主要原因是叠合面间的滑动摩擦,其大小与组合片数、叠合方式、加载情况、位移及润滑状态有关。杨冬冬等[17]基于LS-DYNA显示动力分析方法,对射流式液动锤中的碟簧组进行了应力强度分析,得到满足强度要求的碟簧片数。吕克华等[18]对水力振荡器中碟簧组的研究表明,单片的振幅变形值宜较大,组合碟簧片数不宜过多。纪慧泉等[19]综合理论分析、数值计算、试验结果对组合式碟簧进行对比分析,为电动执行机构碟簧组件的设计提供快速智能化参考。
受井眼及工具直径限制,恒扭矩工具所用碟簧与标准碟簧相比,直径比与高厚比都较小,同时碟簧组的力学特性受组合形式、叠合片数、表面质量及润滑情况等因素的影响较大,已有的文献都是对标准系列中的碟簧组成的固定组合形式的碟簧组进行力学分析,且大多将碟簧变形定义在线性变形阶段内,同时缺乏对满足某种功能需求的碟簧组合设计与优化,采用国标算法的计算值与试验结果相差较大,而标定试验周期又较长。因此,现对非标组合式碟簧展开力学特性研究,以获得最优的组合形式与安装预压量,优化工具性能与总体长度,并为相关工具的研发提供科学指导。
1 非标组合式碟簧力学分析及物理试验
1.1 恒扭矩工具结构及工作原理
恒扭矩工具的具体结构会根据井型及钻采需求进行变化,但其核心结构具有一定的相似性。图1为某种恒扭矩工具的截面图。工具的工作原理可简单概括如下:当钻头施加的反扭矩超过一定限度(也即是启动扭矩值)时,工具中的螺旋花键副压扭转换机构将富余的反扭矩转换为碟簧近一步压缩所需的压力,碟簧在压缩过程中将储存弹性势能,钻头随芯轴发生轴向移动并脱离地层,使得钻头上的反扭矩快速下降,同时作用于碟簧上的轴向力也逐渐减小,并在钻头位移的极限位置处达到瞬态平衡;此后碟簧释放弹性势能,钻头再次恢复至正常钻井工况的位置,并往复循环。

图1 恒扭矩工具剖面简图及单片碟簧Fig.1 Constant torque tool profile and single disc spring
1.2 Almen-Laszlo方法
该方法是基于弯曲梁假设提出的近似解,也简称A-L法,是目前行业广泛采取的计算方法[20]。A-L法对非标组合式碟簧的力学分析是建立在标准单片碟簧轴向负载分析基础上的。单片碟簧在小变形阶段,A-L法与实际结果较为符合;但在大变形阶段,由于未考虑弹簧钢材料本身的非线性特性、轴向及周向应变、阻尼消耗等因素,A-L法的计算值与实际值相比载荷偏小。A-L法的具体计算方法如下。

(1)
其中计算系数为
(2)
式中:F为单片碟簧轴向负荷,N;f为单片碟簧轴向变形量,mm;t为碟簧厚度,mm;E为碟簧的弹性模量,E=2.06×105N/mm2;μ为泊松比,μ=0.3;D为碟簧的外径,mm;d为碟簧的内径,mm;C为碟簧的直径比;h0为碟簧自由圆锥高度,mm;H0为碟簧自由高度,mm;t′为有支撑面碟簧减薄厚度,取厚度t的0.94,mm;K1、K4、C1、C2为A-L解的计算系数。
由单一碟簧构成的组合式碟簧存在如图2所示的3种基本形式,另外还有由不同厚度或组内不同片数组成的混合组合形式。三种基本组合形式的载荷、变形量具有不同的计算方法,具体可参见《碟形弹簧标准》(GB/T1972—2005)[21]。在组合式碟簧变形过程中,其载荷-位移关系一直受阻尼效应的影响。碟簧阻尼力主要由三部分组成:①黏性阻尼,大小与加载速度成正比,与加载方向相反;②库伦阻尼力,主要由碟簧锥面间的摩擦形成,一般为常量,但方向与加载方向相反;③材料阻尼,碟簧材料本身为非线性材料,且在大变形过程中会出现一定程度的塑性变形。
大量的工程实践表明,库伦阻尼力对载荷-位移的影响比重最为突出[22-23]。A-L法在近似求解的过程中仅考虑摩擦阻尼对结果带来的误差,对于复合形式碟簧组,也只考虑叠合表面间的摩擦,修正公式为
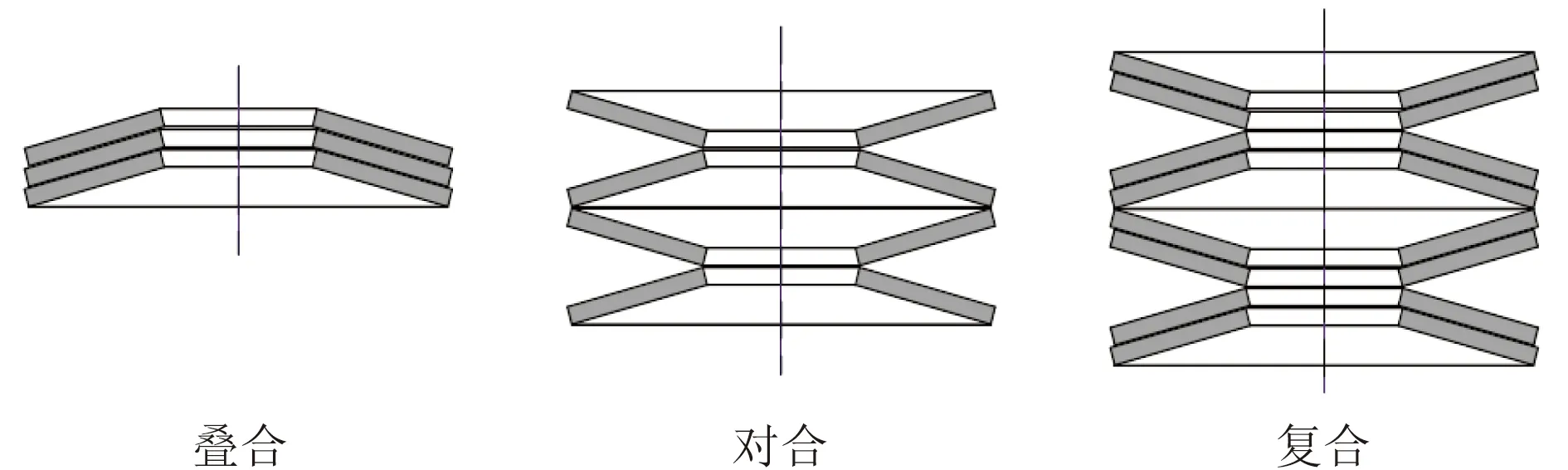
图2 碟簧的基本组合形式Fig.2 Basic combination of disc springs
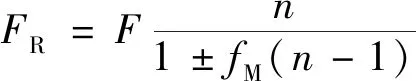
(3)
式(3)中:FR为考虑摩擦阻尼时复合形式碟簧组的负荷;n为碟簧组中叠合部分的叠合片数;fM为碟簧锥面间摩擦因数,推荐取值0.002~0.03,加载时取-号,卸载时取+号。
1.3 物理试验
借助电子万能试验机(图3)对组合式非标碟簧进行物理试验,试验机最大加载力为300 kN,为防止试验过程中碟簧组受载不均,自制上下压板,其中下压板与工作测试台固定,上压板放置于测试碟簧组上,并与试验机活动横梁的下压头保持接触。加载试验分为准静态连续加载和动态加载。准静态连续加载试验用于获取不同润滑状态、不同组合形式下的载荷-位移曲线,并与理论计算的载荷-位移曲线对比得到适用于数值计算的等效摩擦因数及其变化规律;动态加载试验是按不同加载速率对油态润滑下不同组合形式的碟簧从自由状态加载至100 kN时获取的载荷-位移曲线。

图3 试验测试装置Fig.3 Experimental device
2 有限元分析
2.1 有限元模型
对恒扭矩工具而言,既需要组合式碟簧能承载较大的峰值载荷,也需要保证足够的伸缩位移量[24-25]。根据组合式碟簧的载荷与变形特点,叠合部分能够成倍提高承载能力,对合部分能够成倍增加变形,因此复合形式的碟簧组合最能满足恒扭矩工具的性能需求。考虑到叠合片数过多会导致碟簧片间的阻尼增大,叠合部分只考虑了4种形式:两片叠合、三片叠合、四片叠合、五片叠合;对合部分,复合组合的力学性质往往随着对合数的增加呈近似线性的变化规律,因此以最小的两对对合作为研究对象[26]。受井眼及工具内部结构限制,组合所需的单片非标碟簧几何参数如表1所示。
(1)材料属性。弹性段与A-L法定义完全相同;屈服强度取1 500 MPa,塑性段全段的真实应力-应变曲线由相关拉伸试验数据拟合得到,两者共同构成有限元分析的本构方程[27-28]。
(2)网格划分。上下压板视为刚体,碟簧视为变形体。组合式碟簧的网格划分是以单片碟簧为对象进行的,对单片碟簧对称划分成4个区域,每个区域采用扫略方法划分六面体C3D8R单元,单元采用二阶减缩积分算法,考虑到收敛速度,网格细化中保证碟簧在轴向上的网格层数为4层即可。单片碟簧网格划分的结果为节点数71 680,单元数59 520。
(3)接触条件。接触对的设置需要考虑大变形过程中接触区域的扩大问题。接触对一共分成3组,第一组为上压板底面和与之接触的碟簧上支撑面和上锥面;第二组为下压板顶面和与之接触的碟簧下支撑面和下锥面;第三组为剩余组合式碟簧之间的自接触。接触对间的力学性质由准静态连续加载试验确定的等效摩擦因数进行定义。
(4)边界条件。下压板在空间6个方向的自由度设置为固定,上压板仅在竖直方向上具有自由度,加载与卸载过程由上压板位移条件控制。考虑到物理试验中使用导向杆限制碟簧径向上的窜动,对碟簧内圈上X、Z轴方向的一系列特征点限定自由度,设定X轴方向的特征点在Z轴方向的位移为零,即Uz=0;Z轴方向与此类似。在准静态分析中,只需设置一个位移载荷步;在高频循环动载分析中,必须首先预压到一定量,再设置不同频率的周期位移载荷,具体相关参数由数据拟合得到。组合式碟簧中特征点的位置与网格划分结果以五片叠合组合为例如图4所示。

表1 单片碟簧结构参数Table 1 Single disc spring structure parameters
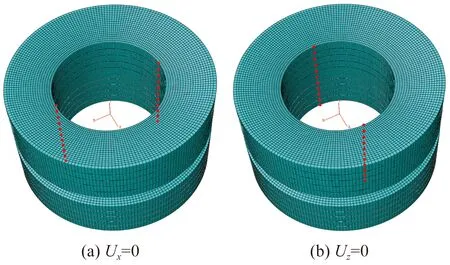
图4 组合式碟簧特征点及网格划分Fig.4 Feature points and mesh division of stacked disc springs
2.2 等效摩擦因数的确定
获得适当的等效摩擦因数是有限元方法准确描述力学特性的前提,但碟簧组间的摩擦因数受表面质量及润滑方式的影响很大,常规试验手段又难以测定。对四种组合形式均采用干态、水态、油态3种润滑条件进行准静态加载试验,获得相应的试验载荷-变形(P-U)曲线。其中干态为直接接触,水态是将组合式碟簧在水中浸润之后测试,油态使用二硫化钼润滑剂对接触部分进行润滑。分别使用A-L法、有限元法计算在不同摩擦因数下的理论载荷-变形曲线,并不断与试验载荷-变形曲线逼近,从而确定不同组合形式在不同润滑条件下适用于A-L法与有限元法的等效摩擦因数,结果如图5所示。
同种组合形式下,随着润滑状态的改善,A-L法与有限元法的等效摩擦因数都随之降低并趋于稳定;同种润滑方式下,随着叠合片数的增加,等效摩擦因数也随之降低并趋于稳定,特别的,在4、5片叠合组合时,两者在相同润滑状态下的等效摩擦因数几乎相等。图5中,A-L法与有限元法采用不同等效摩擦因数逼近试验曲线所得到的载荷-位移曲线与实际试验曲线高度吻合,并由此可知A-L法实际采用的等效摩擦因数比标准推荐值大1~2个数量级。若采用推荐值计算的组合式碟簧A-L刚度解将明显小于实际刚度,载荷值也偏保守。A-L法等效摩擦因数与有限元等效摩擦因数之间的差值随叠合片数增加与润滑条件的改善明显减小,且A-L法等效摩擦因数逐渐落入标准值区间内,并在4或5片叠合组合时达到稳定,以上都说明A-L法求解组合式碟簧力学性能存在明显的弊端。
2.3 准静态循环加载的力学特性
在准静态循环加载情况下,由于阻尼(包括摩擦阻尼与材料阻尼)造成的能量耗散使加载曲线与卸载曲线不重合并形成滞回曲线。若加载过程中产生的功用加载曲线包围的面积Sa表示,阻尼产生的损耗功用滞回曲线包围的面积Sd表示,则功损比为Sd/Sa,利用功能关系,可对组合式碟簧的等效加载/卸载刚度进行计算。图6为不同组合形式下的准静态循环加载曲线与四叠合复合组合下的滞回曲线,图7为不同润滑状态下的等效加载/卸载刚度,功损比,极限载荷变化曲线,由此可初步判定所需的组合形式。
从滞回曲线上看,同种润滑条件下,随叠合片数的增加,极限载荷近似线性增加,损耗功也逐渐增大,但增大的幅度随润滑状态的改善逐渐减小,特别地,在油态条件下,损耗功随叠合片数的增加非常有限;最大变形量均超过9 mm,最终的残余变形量也保持在2 mm附近,且与润滑状态、叠合片数无关。以四叠合复合形式为例,随着润滑条件的改善,损耗功逐渐减小,干态条件的损耗功非常巨大,油态最小,水态与油态的差别不大。刚度曲线中,油态的加载刚度与卸载刚度随叠合片数的增加近乎线性增加,干态与水态则保持非线性关系;同等叠合片数中,加载刚度在干态最大,油态最小;卸载刚度则恰好相反,水态条件的刚度取值则一直位于中间。功损比在4片叠合情况下取得最小值。极限载荷在油态条件下随着叠合片数的增加近乎线性增加,同等片数叠合时,干态条件的极限载荷最大,油态的极限载荷最小,两者的差值随着片数的增多而逐渐扩大。从恒扭矩工具的功能出发,需要减少非必要的阻尼消耗,同时保证300 kN的极限载荷[29-30],由此可确定四片叠合是最优的组合形式,同时需要避免碟簧片间的直接接触。

图5 不同组合形式在不同润滑方式下的等效摩擦因数Fig.5 Equivalent friction coefficient of different combinations in different lubrication modes
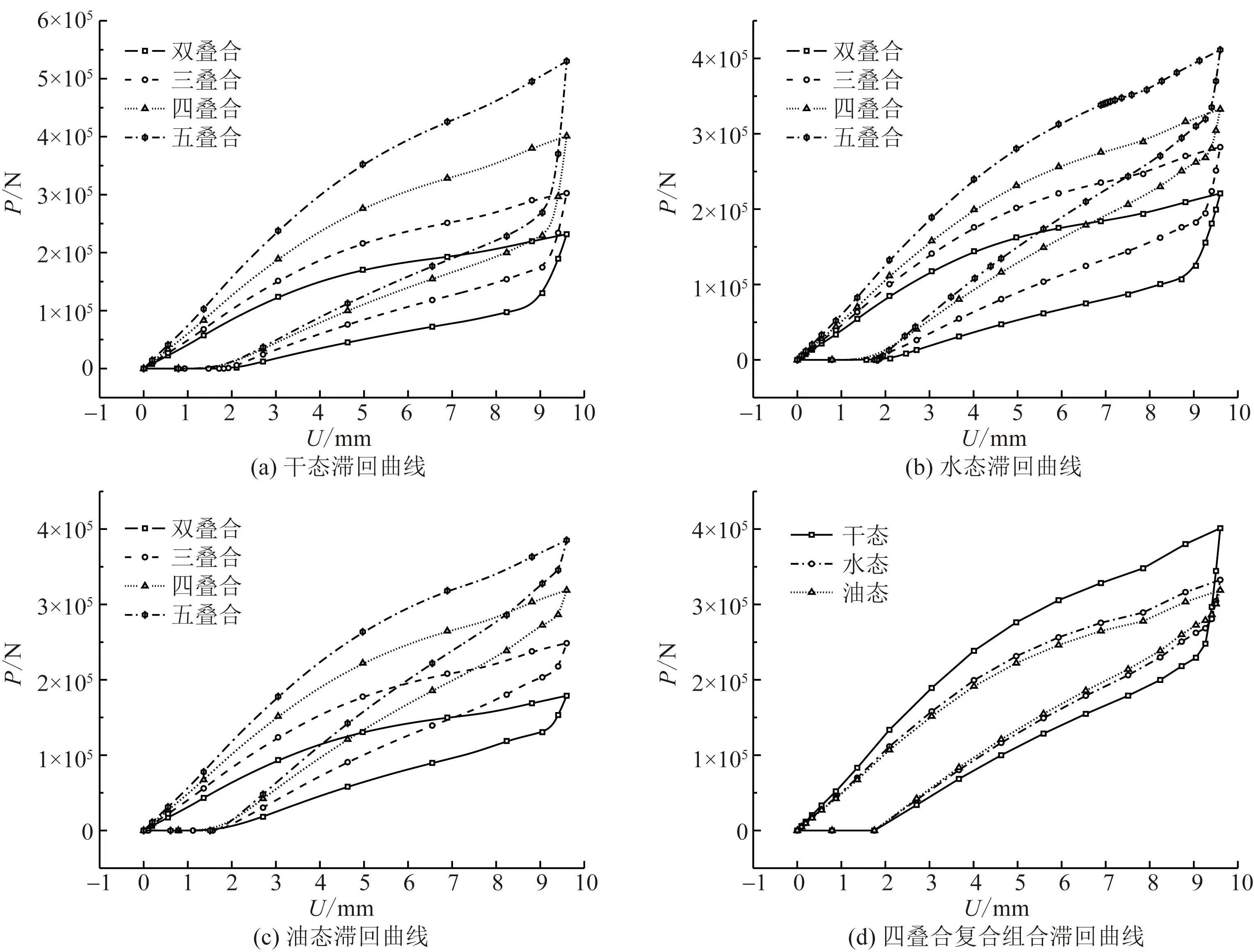
图6 不同组合形式在不同润滑条件下的循环加载Fig.6 Cyclic loading of different combinations with different friction

图7 不同组合形式在不同润滑条件下的力学特性Fig.7 Comparison of mechanical properties under quasi-static cyclic loading
2.4 动态加载试验
加载速率试验是借助电子万能试验机对四种不同形式的组合式碟簧进行动态加载,以油态条件为例,设定加载极限力值为100 kN,通过控制试验机的加载速率分别以2、10、50 mm/min进行加载,探究加载速率对组合式碟簧的力学特性影响。不同组合形式随加载速率变化的力学特性如图8所示。可以看到,在相同叠合片数条件下,随加载速率的增加,加载刚度随之增大;随着叠合片数的增加,加载速率增加导致加载刚度增大的幅度将逐渐减小,特别地,在四片叠合时,加载速率的变化已不对加载刚度产生显著影响,系统较为稳定,这也从试验论证了有限元准静态分析优选出的4片叠合组合形式是可靠的。
2.5 高频循环动载的力学特性
恒扭矩工具在实际工作中要求碟簧组具有一定的行程量,在不同频率的载荷作用下系统具有稳定性;同时也需要进行不同程度的预压,预压量的大小直接决定工具的启动扭矩值[31]。组合式碟簧在确定出叠合片数之后,还需确定出具体的预压量。对于最小单元的复合形式碟簧组,预压量与振幅的和值反映了组合式碟簧的承载极值,因此是相对固定的;而振幅的大小受预压量限制,反映了组合式碟簧的行程范围,并最终决定碟簧组所需的对合组数。以优选出的四叠合复合形式碟簧组为例,在油态润滑条件下,对组合式碟簧在不同频率、不同预压量、不同振动幅值下进行数值分析,从而确定最优的预压量与对合数。由四叠合复合形式碟簧组的滞回曲线可知,碟簧组的承载极值位于9 mm处,为研究预压量与振幅在动载条件下的力学性能,变形量分别取3、5、7、9 mm,并设置了不同的预压量与振幅组合形式;为研究振动频率对组合形式的影响,根据实际工况下工具承载频率一般不超过20 Hz的特点,频率分别取1、2、5、10、20 Hz,对于不同频率,取一个周期进行计算,相关计算结果如图9所示。
碟簧组在高频循环动载下的力学性能是由其滞回曲线来反映的,数值模拟的结果表明滞回曲线仅在卸载段产生较大差异。不同预压量与振幅组合形式的滞回曲线所包围的面积随振动频率的变化呈现一定的规律性:频率1 Hz时包围面积处趋于中间值;随频率增大,滞回曲线所包围的面积先减小后增大,在5 Hz处取得极大值;随频率继续增大,滞回曲线所包围的面积先减小后增大,并在10 Hz处取得极小值,10 Hz之后的面积逐渐增大。由此可知,4叠合复合形式碟簧组的滞回曲线与振动频率之间具有相对一致的变化规律,都对10 Hz频率的振动非常敏感;相同频率下,采用不同的预压量和振幅组合形式不会对滞回曲线的饱满对称性产生显著影响。
在振动频率取敏感值时,碟簧组在不同变形量下的力学特性随预压量与振幅的组合形式表现出不同性质。在变形量一致的前提下,小变形量中(3 mm和5 mm)的预压量越小,滞回曲线越趋于尖锐,无法抵消高频循环动载带来的干扰,系统表现出不稳定性;随预压量的增加,滞回曲线趋于饱满,对称性也逐渐提高,并在预压量为3 mm时,滞回曲线的饱满对称性达到最好,此后再增加预压量,饱满对称性反而下降。大变形量下(7 mm和9 mm),预压量取较小值时,滞回曲线的饱满对称性都表现较好,而随着预压量的增大,预压值与振幅之间的差值逐渐增大,饱满对称性表现变差。预压量相同时,滞回曲线所包围的面积随振幅的增大而明显增大,表明碟簧组中阻尼的能量耗散逐渐增大(包括摩擦阻尼与材料阻尼)。实际工程中,碟簧组在保证稳定性的同时还需尽量减小阻尼的能量耗散,延长碟簧组寿命。考虑到要适当减小工具启动扭矩值、增大碟簧组的行程量,减少碟簧组数量等因素,取预压量3 mm较为适宜,此时最小单元的复合形式碟簧组的最大振幅可达到6 mm,若设计工具所需行程量为120 mm,则最终的碟簧组所需的组数为20组。
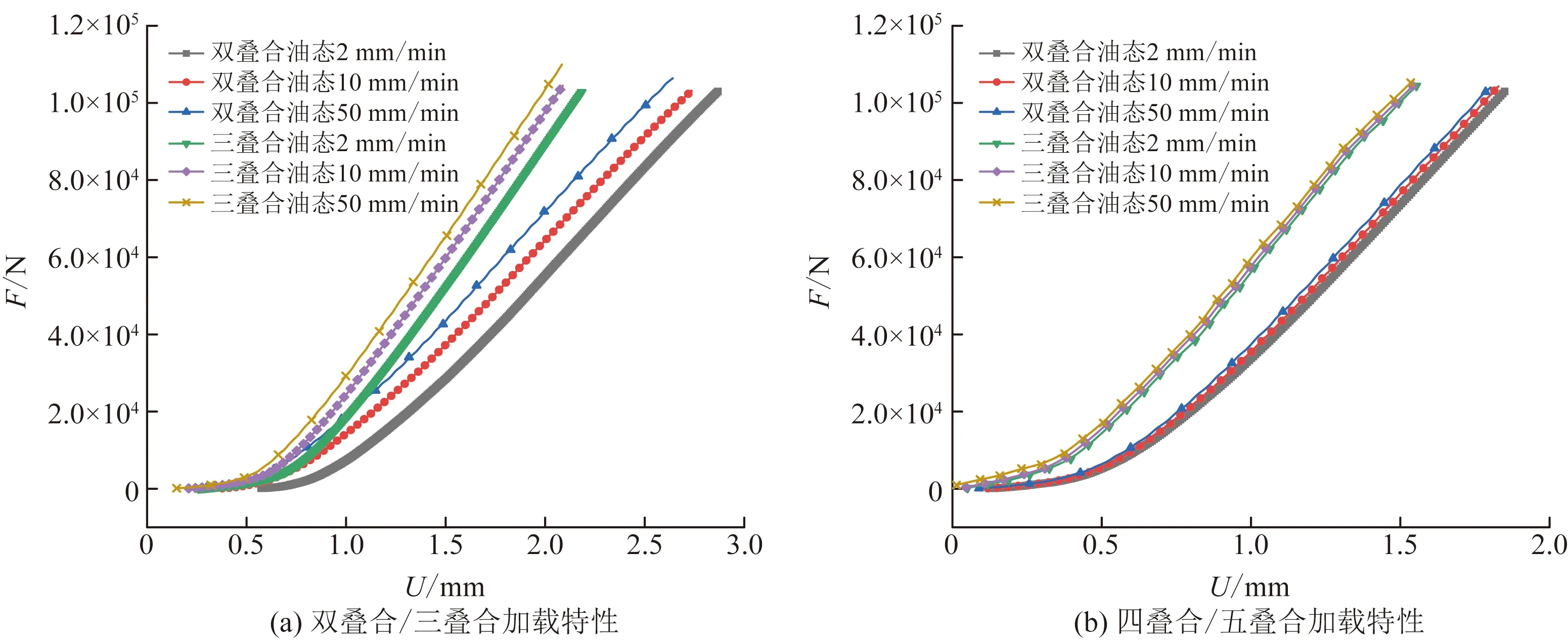
图8 不同组合形式随加载速率变化的力学特性Fig.8 Mechanical properties of different combinations with loading rate
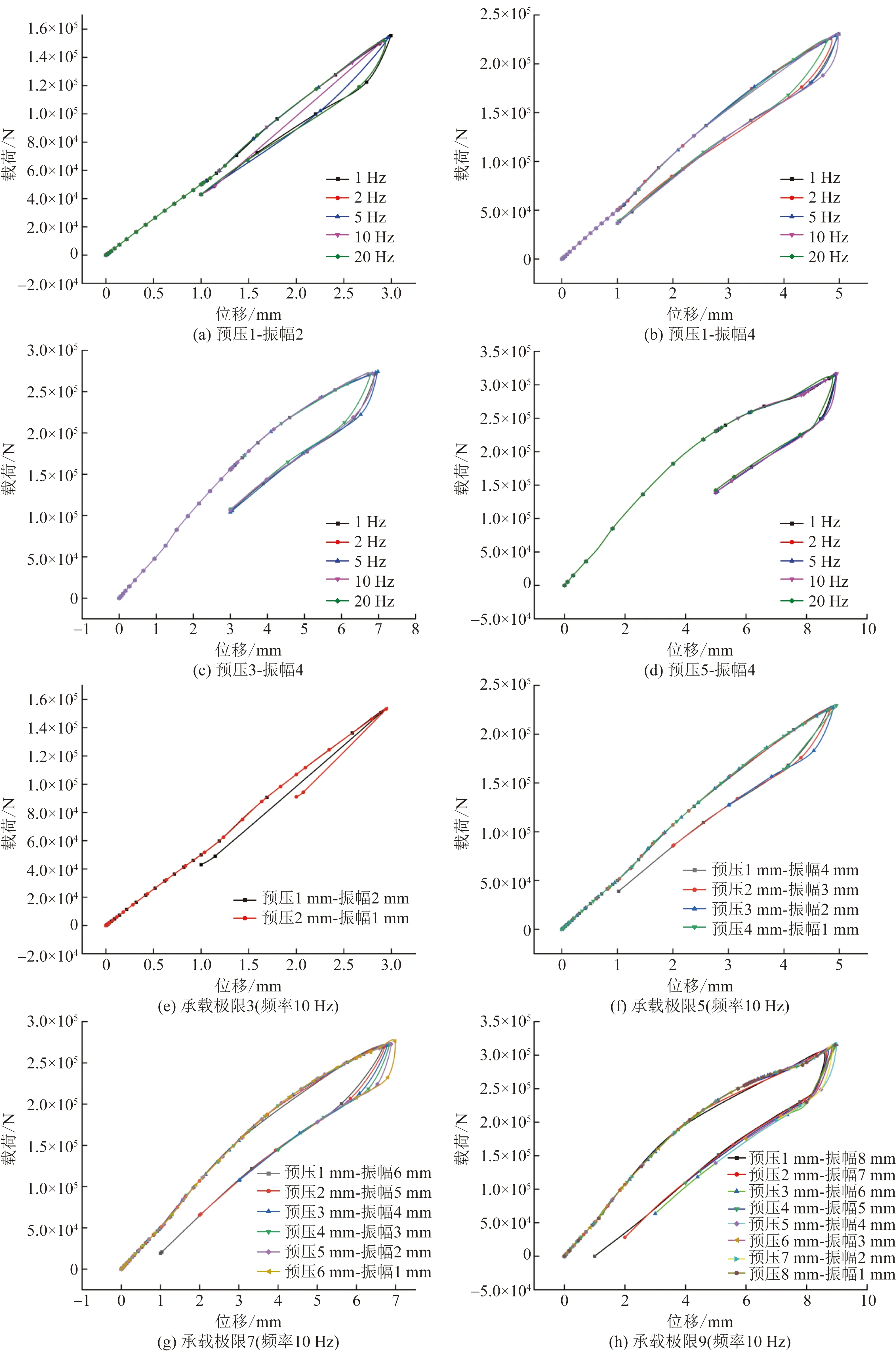
图9 高频循环加载的力学性能Fig.9 Mechanical properties of high frequency cyclic loading
3 结论
(1)常规A-L法计算非标组合式碟簧的力学性能存在较大弊端,产生偏差的主要原因有两点:一是参与A-L法计算的实际等效摩擦因数与设定的标准取值区间差别较大;二是A-L法仅考虑摩擦阻尼而忽略塑性变形引起的材料阻尼。
(2)组合式碟簧的有限元分析必须根据试验加载数据,确定不同组合形式与润滑条件下的等效摩擦因数。随着叠合片数的增加,润滑条件的改善,等效摩擦因数随之降低并趋于稳定。
(3)组合式碟簧的准静态力学分析以损耗功、等效加载/卸载刚度、功损比、极限载荷作为标准,从工具对极限载荷及系统稳定性的要求出发,优选出四片叠合的复合组合形式。
(4)组合式碟簧的动态力学分析结合有限元方法与加载速率试验,分析不同频率、不同预压量与振幅组合形式下的滞回曲线变化规律,从系统稳定性及阻尼耗能的角度出发,确定出最小对合单元的最佳预压量为3 mm,最终碟簧组所需的组数为20组。
