软土地基基坑开挖对坑底桩受力与位移影响的时效分析

江 杰，张 探，欧孝夺*，付臣志

(1.广西大学土木建筑工程学院，南宁 530004；2.广西大学工程防灾与结构安全教育部重点试验室，南宁 530004；3.广西大学广西防灾减灾与工程安全重点试验室，南宁 530004)

在软土地区基坑工程中，工程桩一般在基坑开挖前已经设置完毕，在基坑开挖卸荷过程中，坑底土体会产生回弹位移，土体回弹变形过程中会对桩基产生摩阻力。中性点以上桩周土对桩身作用正摩阻力，以下为负摩阻力，因摩阻力方向相反，桩身处于受拉状态，会对工程桩产生不利影响，甚至会发生坑底工程桩被拉断的事故[1]。因此有必要对开挖后坑底工程桩桩身受力和位移特性进行研究。

目前针对土体回弹对坑底桩基轴力及位移特性影响的研究已有很多，在理论解析方面，胡琦等[2]通过建立桩土界面荷载传递模型，对开挖条件下坑中桩桩周摩阻力的分布、桩基刚度与承载力进行研究；杨敏等[3]利用桩土位移协调和桩体受力平衡提出了一种坑中桩受力与位移的计算方法，通过迭代法和高斯勒让德积分对桩体位移与轴力进行求解；田晓艳等[4]基于两阶段法，将求得的位移施加于桩上建立桩体竖向位移控制方程，采用常数变易法和有限差分法对桩体位移、轴力进行求解。在数值分析方面，曹力桥[5]通过有限元软件对某基坑工程进行数值分析总结出基坑开挖与降水对坑底工程桩变形的影响，发现工程桩对坑底隆起有抑制作用；伍程杰等[6]基于实际工程建立有限元模型对增层开挖后群桩基础的竖向承载特性进行研究。在实验研究方面，纠永志等[7]通过自制的模型桩竖向加荷系统对开挖条件下单桩竖向承载特性、K0系数和不排水抗剪强度对桩侧极限摩阻力的影响进行研究;杨淑娟等[8]结合某基坑工程项目对开挖条件下坑底双排微型钢管桩桩身应力、变化规律等进行分析。但是，上述理论较少考虑时间因素对桩土相互作用的影响。实际工程中，软土在开挖情况下具有较为明显的蠕变效应。师旭超等[9]通过大量的实验研究了淤泥质软土在卸荷条件下土体的回弹规律发现淤泥质土的卸荷回弹分为3个阶段，分别为主回弹变形、次回弹变形和次固结变形(即蠕变)，对于受卸荷作用下的软土地基，其回弹变形在工程应用上来说是很小的，起重要作用的仍然是回弹变形以后的次固结变形。同时，中国经济快速发展，不可避免地在软土地区进行工程建设，且建设规模越来越大，基坑规模与开挖深度随之增加。因此在考虑软土地基基坑开挖蠕变时，合理评价坑底桩基的受力变形和位移特性对制定合理的工程建设和监测方案有重要的意义。

鉴于此，基于软土黏弹性三参量模型，现推导基坑开挖卸荷条件下坑底土体竖向附加应力变化的时域解。通过建立桩体竖向位移控制方程对在坑底土体蠕变变形影响下单桩受力和桩身位移进行研究，提出开挖条件下考虑坑底土体随时间蠕变变形的单桩非线性计算方法。并与数值模拟结果进行对比，验证解析解的有效性，最后对相关计算参数进行分析。

1 计算模型及假设

分析基于以下假设：

(1)在考虑桩基的竖向变形研究时忽略开挖引起的土体侧向位移对桩基的影响。

(2)土体卸荷会发生回弹，在中性点以上土体对桩产生向上的摩阻力，在中性点以下对桩体产生向下的摩阻力，其摩阻力符合Kraft等[10]提出的桩土界面模型(图1)及荷载传递公式。

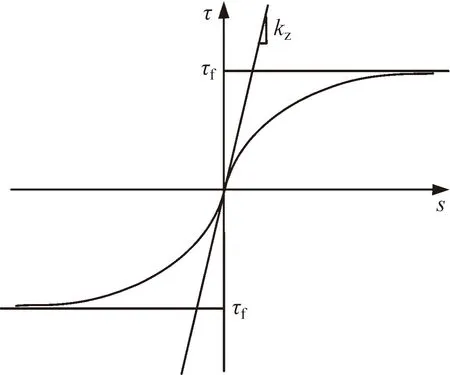
τ为摩阻力；s为桩土相对位移；τf为时间t时桩侧极限摩阻力；kz为桩侧土体的切线刚度图1 卸荷条件下桩-土界面模型Fig.1 Stress-strain curve of the pile-soil interface during excavation

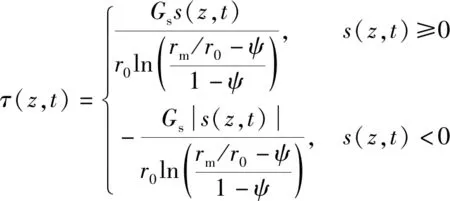
(1)

式(1)中：τ(z,t)为在时间t时深度z处桩侧摩阻力；s(z,t)为时间t时桩土相对位移，s(z,t)=w(z,t)-ws(z,t)，w(z,t)为在时间t时深度z处桩的位移时域解，ws(z,t)为在时间t时深度z处土的位移时域解；Gs为土体小应变时的初始剪切模量；ψ=τ(z,t)Rf/τf，为应力-应变曲线拟合常数；r0为桩界面半径；rm为桩的影响半径。

2 软土地基基坑开挖条件下单桩非线性计算方法

2.1 黏弹性本构模型解答

为了简化蠕变理论分析模型，做以下假设：

(1)假定半无限空间土体为各向同性、均质的黏弹性体，在受力作用下为三向应力状态。

(2)只考虑基坑开挖引起的坑底面土体竖向卸荷因素的影响，忽略分层开挖、围护结构、加固措施及降水等其他附加因素的影响。

(3)球应力张量只引起体积的变化，形状变化只与偏应力张量有关。

已有理论研究表明[11-12]，黏弹性模型可以较好地模拟土体在某一时刻的弹性变形以及土体随时间变化的黏性变形，经典的黏弹性应力应变关系为

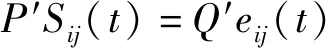
(2)

(3)

式中：Sij为应力偏量；eij为应变偏量；σkk为应力球张量；εkk为应变球张量；P′、Q′、P″、Q″为线性微分算子，其表达式为

对于天然的软土，将土体体积的膨胀看作近似弹性是比较合理的，即

σkk(t)=3Kεkk(t)

(4)

式(4)中：K为体积模量。

利用H-K三参量模型来描述土体蠕变本构关系，此模型由弹性体(H体)和经典Kelvin(K体)串联起来能较好地反映土体卸荷的瞬时变形和随时间的蠕变变形，H-K三参量黏弹性模型满足：

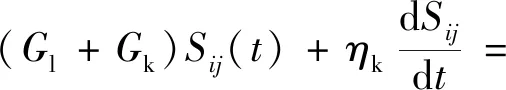
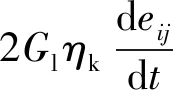
(5)

式(5)中：Gl、Gk分别为H体和K体中的剪切模量；ηk为黏性系数。

将式(4)、式(5)代入线性微分算子中可得

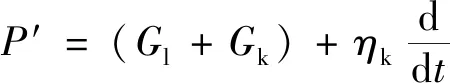
(6)

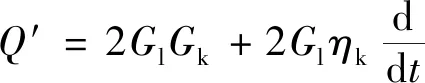
(7)

P″=1

(8)

Q″=3K

(9)

对式(6)～式(9)进行Laplace变换可得

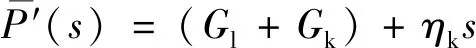
(10)

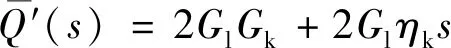
(11)

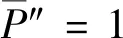
(12)

(13)

根据弹性-黏弹性对应原理，可得弹性模量E(s)和泊松比μ(s)表达式，并将式(10)～式(13)代入表达式进行Laplace变换可得

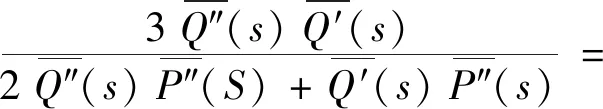
(14)

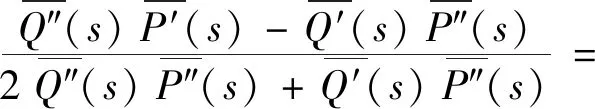
(15)

2.2 坑底土体开挖卸荷引起的附加应力时域解

设基坑底部因卸荷产生的均布荷载P(t)=P0H(t)，其中H(t)为 Heaviside 函数，表达式为

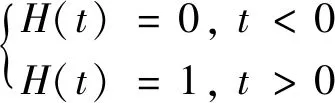
(16)

对P(t)进行Laplace变换可得

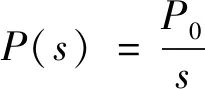
(17)

徐志英[13]利用Mindlin对半无限空间内受均布荷载的土体进行求解得出竖向应力分布并进行了简化，将式(14)、式(15)、式(17)代入简化式中即可得到受竖向集中荷载时土体竖向应力的Laplace变换表达式为

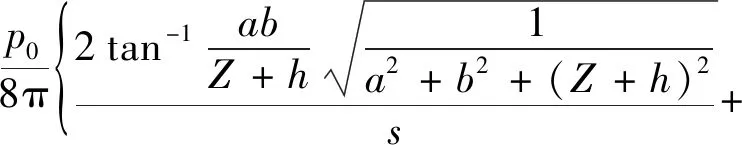
(18)

式(18)中：P0为坑底竖向均布荷载；a为基坑长度；b为基坑宽度；h为待求应力点距离坑底的距离；Z为待求应力点距离地面的深度。

(19)

(20)

对式(18)进行Laplace逆变换即可得到在竖向荷载作用下土体竖向应力随时间变化的解，即

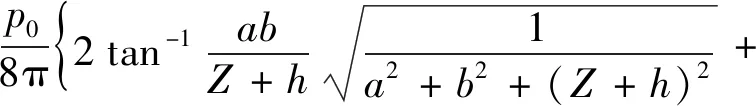
(21)

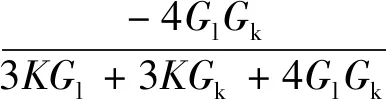
(22)

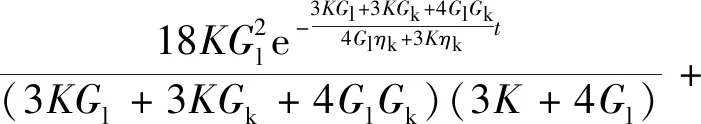
(23)

2.3 基坑开挖卸荷时坑底土体回弹变形计算

坑底土体在基坑开挖卸荷时，将会产生回弹变形，在附加应力作用下，土体回弹变形量[14]为

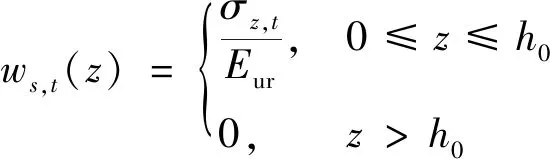
(24)

式(24)中：σz,t为时间t时深度z处竖向应力；h0为卸荷影响深度，由公式h0=he/(0.061 2he+0.19)确定，其中he为基坑的开挖深度；Eur为坑底土体卸荷模量。

2.4 桩侧极限摩阻力计算

龚晓南等[15]通过建立单桩模型，利用Mindlin应力解考虑开挖引起的竖向有效应力变化得到了开挖后桩侧土体的极限阻力。

在开挖深度H处土体引起的竖向有效应力减少为

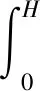
(25)

开挖后单位面积内桩侧极限摩阻力为

fs,t=(1-sinφ)OCRsinφ(γZ-pt)tan(0.6φ)

(26)

式(26)中：φ为土层内摩擦角；OCR为土体固结比，其数值等于开挖前后竖向有效应力之比；γ为土层重度加权值。

对fs，t积分可得桩长范围内桩的极限摩阻力为

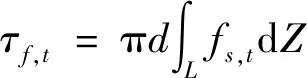
(27)

式(27)中：d为桩基直径。

2.5 软土地基基坑开挖条件下对坑底单桩轴力影响的时域解

取桩身一微小单元进行分析，由静力平衡条件可得

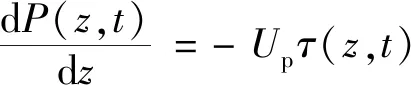
(28)

式(28)中：Up为桩的周长；P(z,t)为在时间t时深度z处桩身轴力；τ(z,t)为时间t时深度z处桩身所受的竖直方向的摩阻力。

桩体微小单元体的压缩变形为

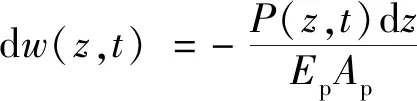
(29)

联立式(28)、式(29)可得桩身控制方程为

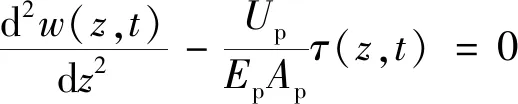
(30)

式(30)中：Ep为桩的弹性模量；Ap为桩的横截面积。

桩侧土体的切线刚度为

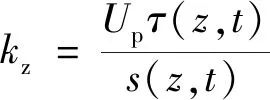
(31)

则初始切线刚度为

(32)

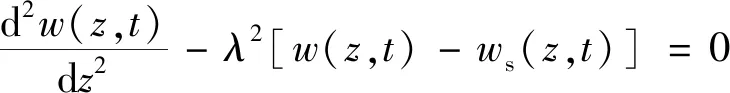
(33)

采用有限差分法对软土卸荷条件下桩基变形内力进行研究，将单桩沿桩身均匀的分为n个单元，在桩顶和桩端分别增设一个虚拟节点，编号为-1和n+1。

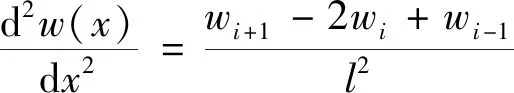
wi-1-(2+λ′2ih2)wi+wi+1=-λ′2ih2ws,i

(34)

式(34)中：ws,i为桩侧土体在节点i处位移。

桩侧土体割线刚度的差分形式为

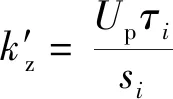
(35)

此时应满足方程的边界条件，桩顶自由支承，桩端在卸荷时土体隆起会对桩体产生上抬力使桩端与土体分离。在桩顶桩端的轴力均为0，有

(36)

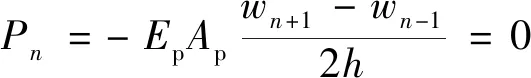
(37)

对式(36)、式(37)求解并代入式(34)中可得

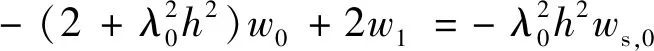
(38)

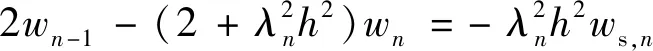
(39)

对桩身控制方程和边界条件进行离散，由式(34)、式(38)、式(39)可得方程解得卸荷条件下单桩的竖向位移场，方程组为

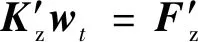
(40)

式(40)中：wt为桩身节点竖向位移时域解，其表达式为wt={wt,0wt,1…wt,i…wt,n-1wt,n}T;F′z为桩身节点上的荷载向量，其表达式为F′z={-λ′02h2ws,0-λ′12h2ws,1…-λ′i2h2ws,i…-λ′2n-1h2ws,n-1-λ′n2h2ws,n}T；K′z为桩身刚度矩阵，其表达式为

(41)

式中:Ai=-(λ′i2h2+2)。

对式(40)求解可得到沿桩身的竖向位移解答方程,其桩身位移可解得

wt=K′z-1F′z

(42)

卸荷条件下单桩位移非线性时效分析求解过程如下。

(1)将开挖部分土体的自重应力反方向加载在基坑开挖后的底部，由式(24)求解出在基坑开挖后不同时间时沿桩身回弹的自由土体位移场ws,t=0(z)。

(2)设置桩身初始节点位移w=0，解得桩土相对位移s(z)=wt(z)-ws,t(z)，进而求出桩身节点切线刚度。

(3)用式(42)求出新的节点位移用新求出的桩身节点位移求出桩土相对位移和新的割线刚度，用新的割线刚度求出新的节点位移。

3 方法验证

为验证坑底土体蠕变变形下单桩的非线性解，利用有限元软件中自带Burgers土体蠕变本构模型分析时间效应的影响，利用FISH语言屏蔽掉Burgers模型中M体黏性系数从而获得与理论一致的参数用于进行数值模拟。基坑尺寸为30 m×20 m，开挖深度10 m，模型尺寸为150 m×100 m×50 m，设计此尺寸为了避免边界尺寸效应的影响；土体弹性模量Es为10 MPa，密度为1.89 g/cm3，泊松比为0.33；桩基直径1 m，桩长10 m，弹性模量Ep为30 GPa；H体中的剪切模量Gl=0.35 GPa，K体中的剪切模量Gk=0.2 GPa，体积模量K=0.65 GPa，黏性系数ηk=2.24 GPa·d。桩顶无约束，桩端自由，利用有限元软件进行模拟，与计算结果进行对比。结果如图2所示，在时间t=0和t=70 d时数值模拟结果和本文解结果能够较好地吻合，验证了本文方法的有效性。

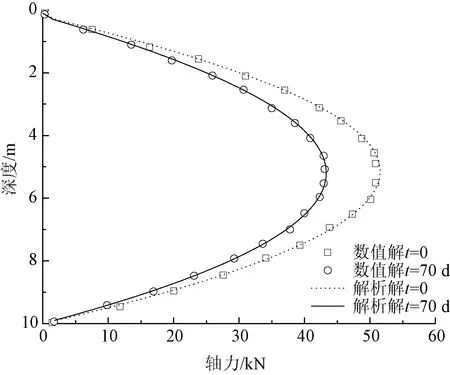
图2 桩身轴力随时间的变化曲线Fig.2 The variation curve of axial force of pile with time

4 参数分析

基本参数如下：桩径1 m，基坑尺寸为30 m×20 m，开挖深度10 m；土体弹性模量Es取值为10 MPa，重度1.89 g/cm3，泊松比0.33；坑底桩基直径1 m，桩长20 m，桩体弹性模量Ep取值为30 GPa；H体中的剪切模量Gl=0.35 GPa，K体中的剪切模量Gk=0.20 GPa，体积模量K=0.65 GPa，黏性系数ηk=2.24 GPa·d。桩顶无约束，桩端自由。

4.1 时间因素的影响

考虑土体蠕变变形影响下坑底桩身轴力随时间的变化如图3所示，桩基轴力随时间增加而逐渐减小，在开挖后30 d桩身轴力减少速度较大。在0～10 d内减少速率最大，达到峰值，在第30～70 d时，其减少速率逐渐下降，在70 d时已经基本达到稳定。开挖时桩身位移与时间的曲线如图4所示，其变化规律和桩身轴力相同，在开挖后30 d内桩身位移变化速率较大，30～70 d时其桩身位移变化速率逐渐减少并趋于稳定。基坑开挖后30 d内是对桩身轴力和桩身位移影响最大时间段，在实际工程中应加强此时间段内桩基变形的监测，降低坑底土体蠕变的不利影响。基坑在刚开挖完以后回弹变形最大，应及时加注底板降低坑底土体的隆起变形。

4.2 开挖深度的影响

为研究基坑开挖深度对坑底单桩承载力的影响，分别取0.2H、0.5H、H、1.5H，其中H为开挖深度10 m，在开挖卸荷条件下不同开挖深度对单桩桩身轴力的影响如图5所示。在开挖0.2H～H深度时，桩身轴力对开挖深度的增加而增大，在0.2H～0.5H时，桩身轴力增大幅度较大。当开挖深度进一步增加时，桩身轴力随开挖深度的增加而减小，在开挖深度达到1/2桩长时桩身轴力值达到最大值。开挖深度对桩身位移的影响如图6所示，开挖深度与桩身位移近似呈线性关系，开挖深度越大，桩身回弹位移越大。

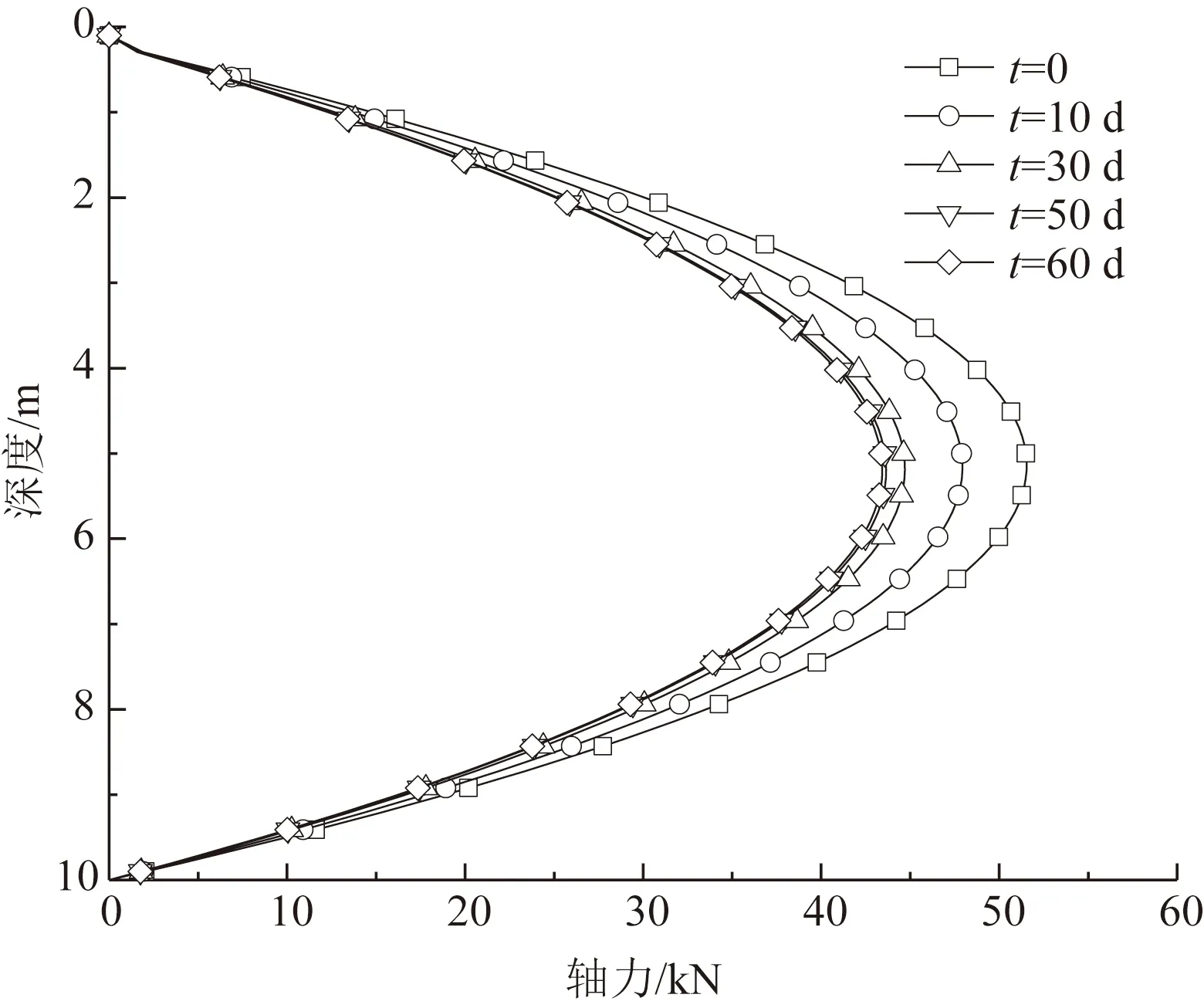
图3 开挖后不同时间对桩身轴力的影响Fig.3 Influence of different time after excavation on axial force of pile

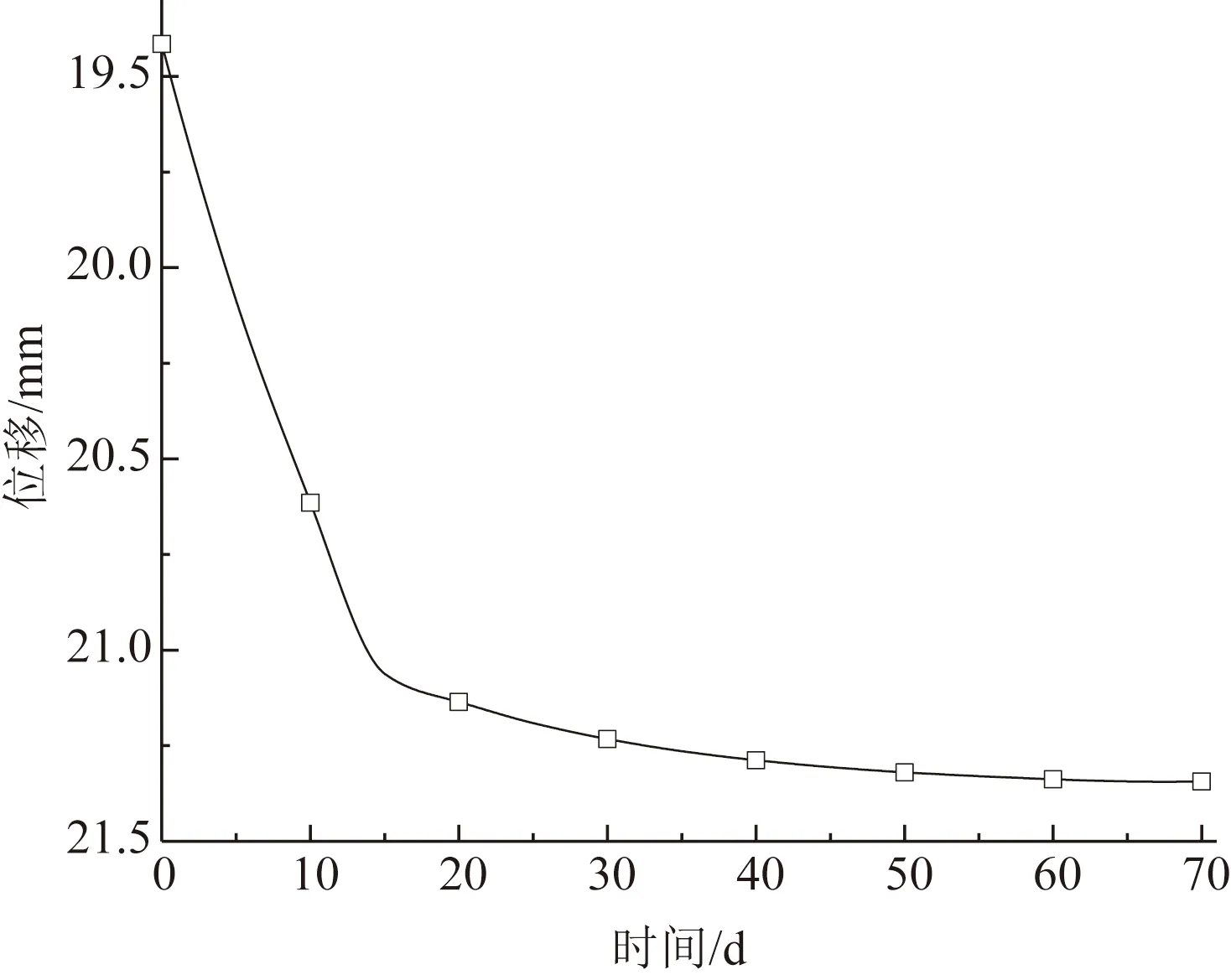
图4 开挖后不同时间对桩身位移的影响Fig.4 Influence of different time after excavation on pile displacement

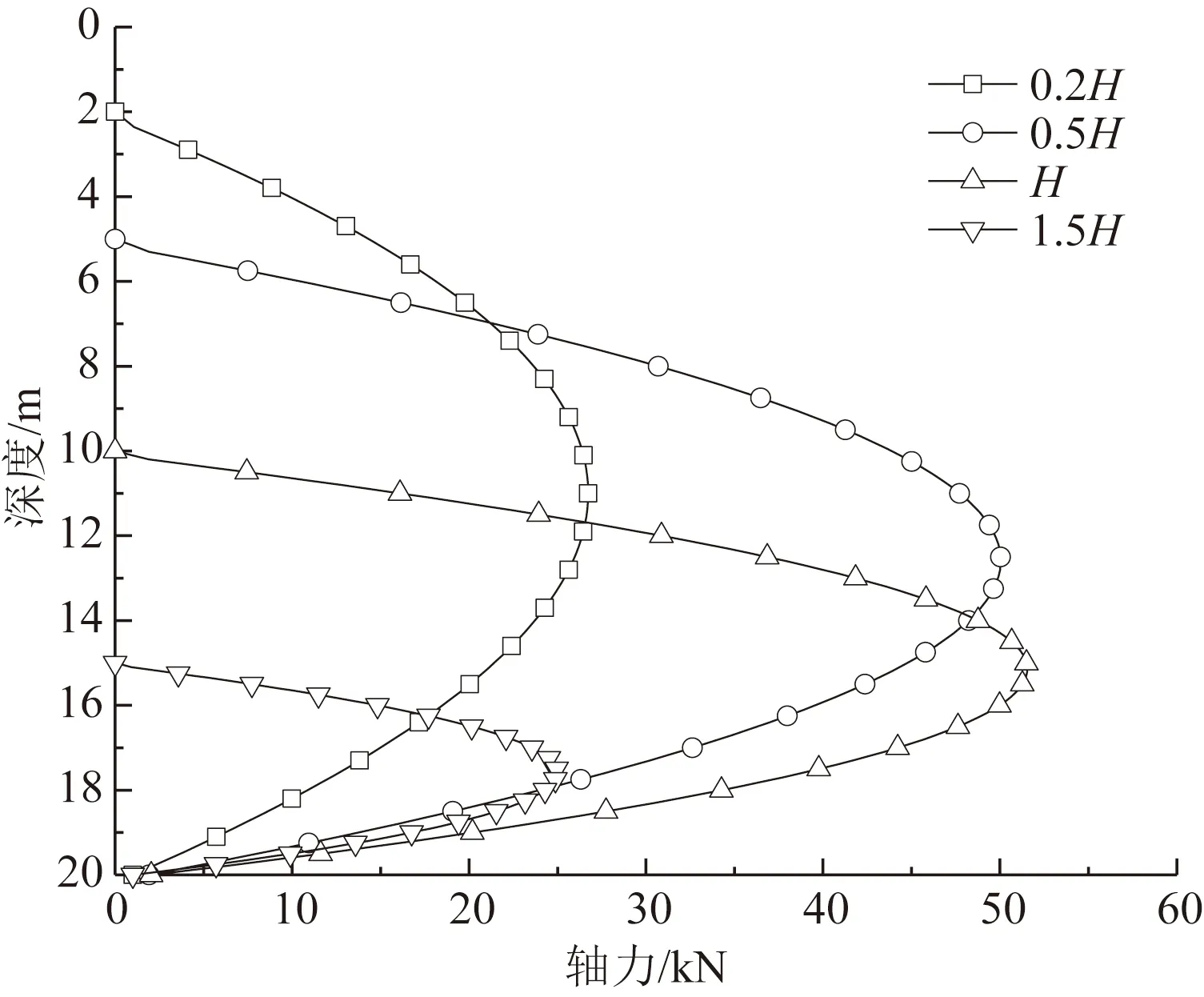
图5 不同开挖深度对桩身轴力的影响Fig.5 Influence of different excavation depth on axial force of pile

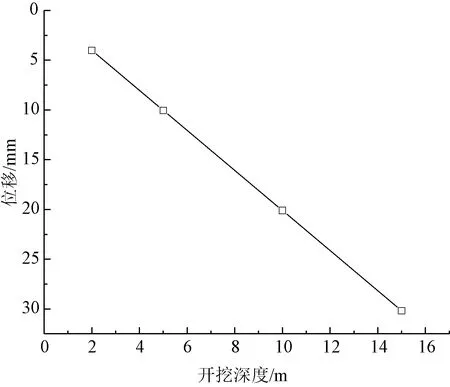
图6 不同开挖深度对桩身位移的影响Fig.6 Influence of different excavation depth on pile displacement

5 结论

(1)通过引入H-K三参量模型，提出了基坑开挖引起坑底土体附加应力的时域解。在此基础上对桩土相互作用进行分析，建立桩身控制方程，并通过有限差分法和迭代法求得坑底桩基桩身轴力与位移的时域解。

(2)结合三维有限元算例验证了本文方法的适用性和合理性。采用提出的基于H-K三参量黏弹性模型的计算方法，能够较为准确地预测软土基坑开挖卸荷条件下坑中单桩桩身轴力和桩身竖向位移随时间的发展趋势，可为相关工程提供理论支撑。

(3)计算结果表明，在基坑开挖后30 d内桩身轴力减少和桩身位移变化速率较大，30～70 d时其变化速率逐渐减少并趋于稳定。在实际工程中应加强此时间段内桩基变形和桩身位移的监测。

(4)计算结果表明，开挖深度对轴力的影响较大，在开挖深度小于桩长时，桩身轴力随开挖深度的增大而增大，当开挖深度达到一定值时，桩身轴力随开挖深度的增大而逐渐减小。开挖深度与桩身位移近似呈线性关系，开挖深度越大，桩身位移越大。