强震作用下混凝土框架结构的地震失效模式

赵仰康，宋鹏彦，王 岳

(1.河北大学建筑工程学院，保定 071002；2.河北省土木工程监测与评估技术创新中心，保定 071002)

混凝土框架结构是目前中国城市建设中常见的结构，2008年汶川8.0级大地震、2010年青海玉树7.1级地震、2014年芦山地震等，造成大量建筑物的倒塌、破坏以及人员的伤亡。人民的人身安全、财产安全未得到保证，国家经济也受到一定影响，研究框架结构的地震失效模式，对于框架结构抗震及加固具有重大意义。

结构在地震作用下的破坏过程是一个损伤非线性发展与随机演化的过程。对框架结构而言，结构自身的不确定性和地震动记录输入的随机性，在双重不确定性因素的影响下，框架结构在不同地震动作用下的动力响应分析是随机的、不可预测的。近些年来，中外许多学者对框架结构在地震作用下的失效模式进行了一系列的研究，Elwood等[1]基于振动台试验，研究了钢筋混凝土(reinforced concrete，RC)框架结构的轴压和剪切失效模式；朱俊锋等[2]采用Monte-Carlo方法考虑了地震动的随机性，研究了在不同地震动激励下，多层框架结构的失效模式；沈霄鹤等[3]、单兵等[4]基于Pushover分析方法，分别对巨型钢框架结构和RC框排架主厂房结构进行了地震失效模式研究；白久林等[5]、马恺泽等[6]采用增量动力分析法，考虑地震动的不确定性，分别对RC框架结构失效模式进行优化、钢框架-混凝土剪力墙结构进行相关研究；吕大刚等[7]采用结构可靠度理论，对RC框架结构3类层间失效模式及3种控制失效模式的相对发生概率进行相关研究。于晓辉等[8]、刘流等[9]基于可靠度理论中的割集方法，考虑了地震动的随机性，分别对结构典型失效模式、掉层框架结构典型失效模式发生的概率进行了相关性研究；徐龙河等[10]提出基于概率的地震失效模式识别方法并且建立了失效模式下结构失效概率关系表达式，考虑了构件损伤。贾明明等[11]对摇摆桁架-防屈曲支撑-钢框架体系进行了不同地震作用下失效模式分析和抗震性能的研究，考虑了地震动的不确定性。

综上所述，地震作用下框架结构的抗震安全性备受关注，但目前大多数学者对框架结构的研究只考虑了小、中、大震，忽视了巨震对结构造成的影响。因此，为了保证框架结构的安全、稳定，对框架结构在巨震作用下的研究就显得极为重要。故现以中国广泛存在的钢筋混凝土框架结构为研究对象，基于OpenSees平台建立RC框架结构的有限元数值模型，考虑地震动输入的不同，采用非线性动力时程法探索框架结构的地震失效模式。研究结果对于框架结构抗震设计和抗震安全性评价具有重要的工程实际意义。

1 框架结构地震失效模式

钢筋混凝土(reinforced concrete,RC)框架结构，在地震作用下有许多失效模式，不同学者对错框架结构的失效模式分类不同。主要失效模式有三类，分别为屈服失效模式、柱极限弯曲失效模式和柱极限剪切失效模式[12]。其中屈服失效模式包括单层屈服失效模式、全梁失效模式和部分梁屈服失效模式；柱极限弯曲失效模式包括边柱、中柱极限弯曲变形两种类型；柱极限剪切失效模式包括边柱和中柱极限剪切变形失效模式，共7种。对于单层屈服失效模式，部分梁屈服失效模式，结构的损伤全部集中在楼层的某一层或者某几层，使得该楼层的变形急剧增大，从而出现侧向倒塌行为。此时，构件中仅有局部构件发生屈服并进入弹塑性状态，而其他未失效楼层的构件大多处于弹性状态，其材料的抗震潜能未能充分发挥，结构的耗能能力未能达到最大化，最终使得结构在破坏时的承载能力和变形能力都较小。对于全梁失效模式，即“强柱弱梁”[13]理想失效模式，所有梁端和首层柱底发生屈服，形成梁端耗能机制，各楼层具有相同的侧移，结构承载能力和变形能力最强，延性最好，是地震作用下希望出现的最理想的失效模式。

2 钢筋混凝土结构的选取

2.1 结构模型的确定

以某6层RC框架结构为例[14]。结构设防烈度均为8度(0.2g,g为重力加速度)，场地类别、设计地震分组分别为Ⅱ类、第二组；底层高为3.9 m，其他层均高为3.3 m，边跨为6 m，中跨为2.4 m；标准层活荷载为2.0 kN/m2，标准层恒荷载为4.5 kN/m2，屋面活荷载为0.5 kN/m2。RC框架结构模型图如图1所示。

对以OpenSees平台建立钢筋混凝土框架结构的有限元模型进行分析。在建模时，假设RC框架结构模拟采用杆系模型，以梁、柱为基本单元；底端柱与地面连接方式为固接；忽略墙、楼板的影响。

梁、柱均采用集中塑性铰单元，能够精确地模拟框架侧移；对应节点连接方式为刚性连接；截面采用纤维截面。混凝土材料采用Concrete01，其参数由Kent-Scott-Park模型确定；钢筋采用考虑Bauschinger的Steel02本构。图2、图3分别给出了Concrete 01、Steel 02本构模型，其模型参数由图2、图3确定，其中混凝土参数的具体物理力学指标如表1所示。并考虑重力二阶(P-δ)效应的影响。

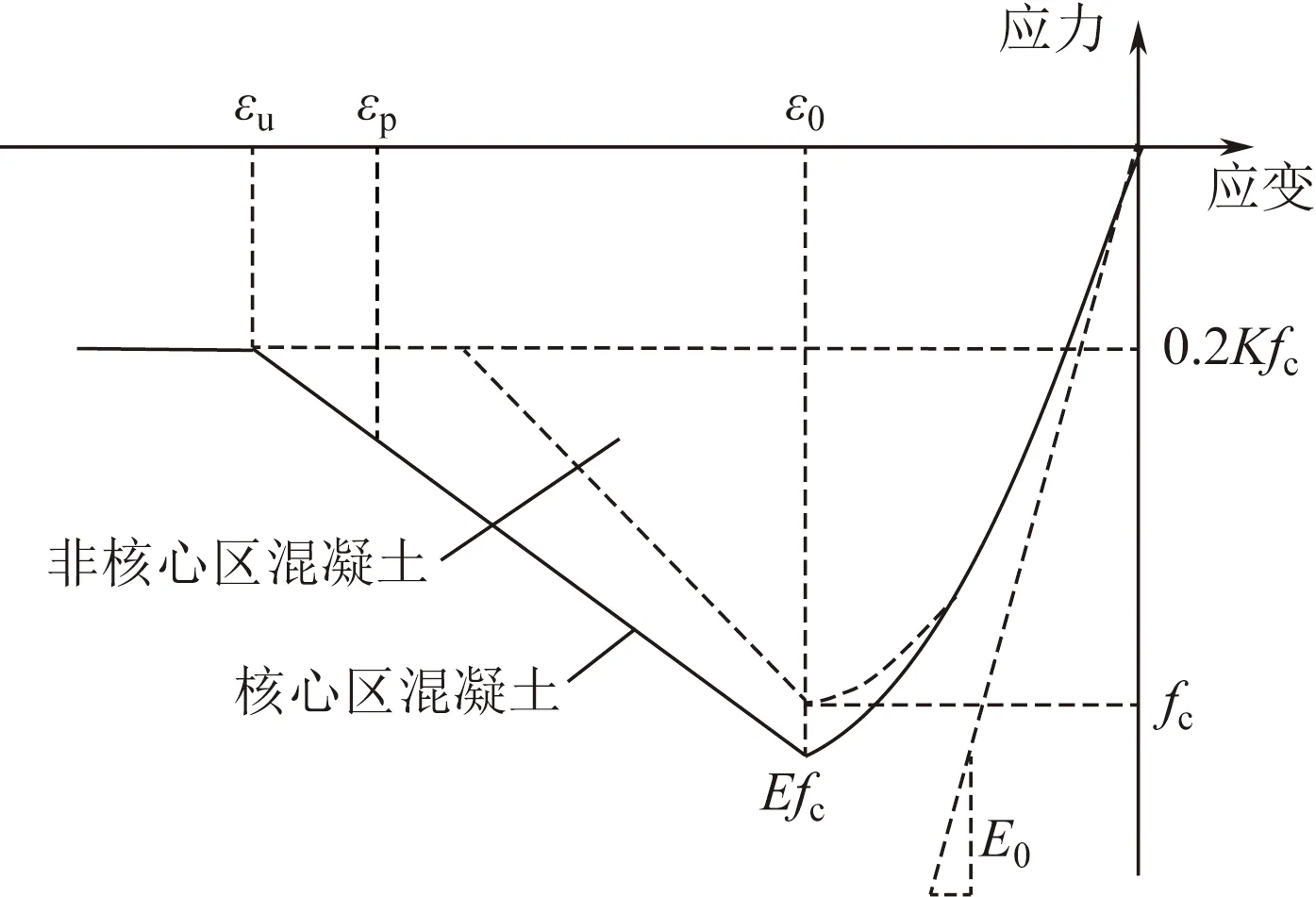
fc为峰值应力；ε0为峰值应变；εp为任意一点应变；εu为极限应变；E为弹性模量；E0为初始弹性模量；K为箍筋约束对核心区混凝土强度的增大系数图2 Concrete 01本构模型Fig.2 Concrete 01 constitutive model

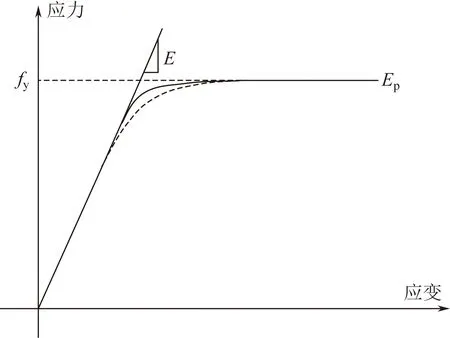
fy为屈服强度；Ep为弹性模量图3 Steel 02本构模型Fig.3 Steel 02 constitutive model

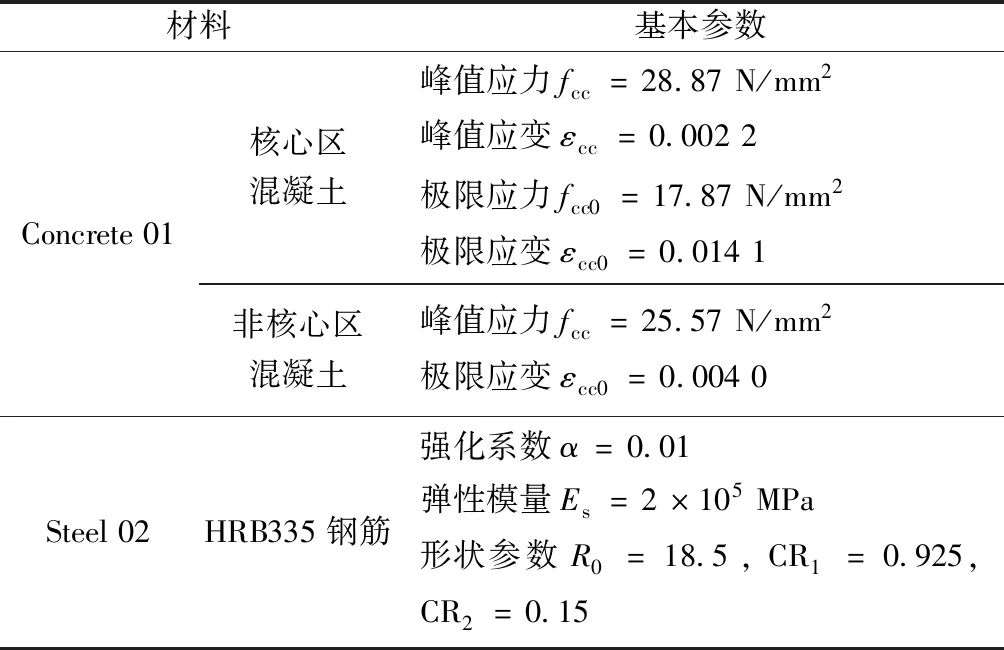
表1 OpenSees模型参数Table 1 OpenSees modeling parameters

根据振型分析表明该结构的基本周期为1.040 7 s。

2.2 地震动的选取

地震动记录输入的随机性是判断混凝土框架结构地震失效模式结果准确性的决定性因素，而地震动不确定性因素：震级、震源机制、场地效应、距离和强度大小等重要参数对地震动的影响很大。由于获得实际场地的历史地震动可能性较低，故通常选取有代表性的地震动。采用文献[15]中的20条地震动记录用来考虑地震的不确定性。图4给出对应大震作用下(0.4g)结构各层层间位移的变化趋势图，可见，20条地震动对应的结构各层层间位移变化中，可以将结构的层间位移变化分为3类：薄弱层不明显、薄弱层由第2层控制、薄弱层由第4层控制。故从20条地震动中选取3条具有代表性的地震动来进一步分析结构的失效模式。表2为地震动的基本信息，图5为选取的3条地震动的时程曲线图。

3 基于非线性动力时程分析的结构失效模式

多个构件失效逐步累积引起整体的结构失效。其失效模式由构件的不同失效类型和失效顺序组合形成。在数值模型中，结构塑性铰的发展过程可以直观反映结构失效模式特征，对于框架结构而言，梁、柱构件出现不同破坏程度，塑性铰的顺序均可体现。随着结构进入塑性阶段一定范围，结构变形会逐渐变大，通过限制结构的变形来约束结构达到破坏状态，采用层间位移角来判别结构失效。中国现行《建筑抗震设计规范》(GB50011—2010)中规定的混凝土框架结构极限最大层间位移角为1/50。考虑结构几何非线性和材料非线性，开展不同地震动下的RC框架结构的地震失效模式研究，主要考虑梁柱塑性铰出现的概率和梁柱塑性铰失效顺序以及层间位移角。

图4 大震作用下(0.4g)结构各层层间位移变化趋势Fig.4 The displacement trend diagram of each layer of the structure under the action of a major earthquake (0.4g)

表2 地震动信息Table 2 Ground motions information

3.1 大震作用下RC框架结构的失效模式分析

基于所选取的3条地震动记录来考虑地震动的不确定性的影响，调幅地震动峰值加速度(peak ground acceleration，PGA)为0.4g，采用非线性动力时程方法对RC框架结构在不同地震动作用下的失效模式进行分析，以柱或梁两端的钢筋屈服来确定构件塑性铰的形成。图6为所选3条地震动加速度反应谱，表3为结构周期对应的层间位移角。从图6可以看出，对应大震作用下(PGA=0.4g)，结构的最大层间位移角没有超过规范规定值1/50。

图7给出在大震作用下(0.4g)边柱构件底侧一截面，核心区内一点(A点，在图1中体现)的混凝土应力应变曲线和钢筋的应力应变曲线，进入非线性阶段。由于地震动是往复变向的，故可以认为结构在地震作用下就相当于若干次大小不同的Pushover作用。钢筋的应力应变曲线服从弹塑性关系，反映了在地震作用下的耗能，并产生了包辛格效应。RC框架结构在不同地震动作用下，峰值加速度PGA均为0.4g时，结构的失效模式如图8所示。图中，圆点颜色的不同表示结构的最大层间位移所处区间状态。

从图8可以看出，在相同强度的不同地震动输入下，塑性铰出现的差别有很大区别，塑性铰并不是突然出现的，而是随着地震动的输入，在一定时间内，塑性铰最先出现在梁端，一般出现在梁的两端。由于地震动的不同，同一结构塑性铰出现的顺序不同，遭到的破坏程度不同。当峰值加速度PGA=0.4g时，图8(a)中只在1～4层的梁端出现了塑性铰，体现了中间层梁屈服失效模式；图8(b)、图8(c)中1～4层，梁端出现塑性铰后，底层柱的柱端也开始出现塑性铰，上层5～6层梁端塑性铰是在柱端出现塑性铰之后才出现的，并且遭到了严重破坏。图8(b)、图8(c)中分别在柱端出现了4个、9个塑性铰。这和层间位移信息(图4)有一定的差别，图4中地震动2作用下薄弱层主要体现在2层，而地震动3作用下体现在4层。

图6 地震加速度反应谱曲线(0.4g)Fig.6 Seismic acceleration response spectrum(0.4g)

表3 结构对应的层间位移角Table 3 Story drift angle of structure

图7 钢筋混凝土应力应变曲线 Fig.7 RC strees-strain curve

3.2 巨震作用下RC框架结构的失效模式分析

由于地震动与结构的相互作用并不是简单的线性关系，因此随着峰值加速度的不同，结构的塑性铰出现并不一定按照特定的规律进行发展。进一步采用《建筑抗震设计规范》(GB50011 —2010)、《中国地震动参数区划图》(GB18306—2015)和吕大刚等[16]提出的结构设防烈度为8度(0.2g)对应的巨震地震动强度，将所选取的3条地震动强度的峰值加速度分别调整为建议的巨震峰值加速度，即PGA取0.580g、0.620g、0.719g、0.580g、0.825g，采用非线性动力时程分析法进行不同峰值加速度下混凝土框架结构的失效模式分析。图9给出了巨震作用下的峰值加速度0.580g、0.825g对应的加速度反应谱，对应的结构谱加速度列入表4中，可见考虑结构特性，对应的谱加速度的差别较大。图10为3条地震动在不同峰值加速度下的层间位移角，表5为在巨震作用下结构最大层间位移的信息。

●θmax<1/250;●1/120<θmax<1/60;●1/250<θmax<1/120;●θmax>1/60图8 大震作用下(0.4g)结构塑性铰分布Fig.8 The plastic hinge distribution corresponding of major earthquake(0.4g)

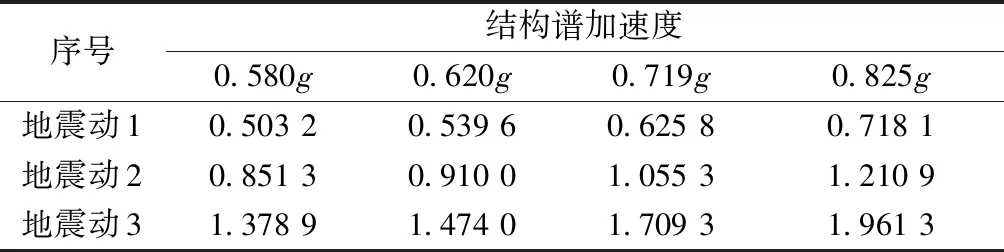
表4 结构谱加速度Table 4 Spectral acceleration of structural

图9 地震加速度反应谱曲线Fig.9 Seismic acceleration response spectrum

表5 结构的最大层间位移信息Table 5 Inter-story drift angle of structural

从图10可以看出，对于同一条地震动，随着峰值加速度的增大，结构的层间位移角也增大，其变化趋势大致相同。在地震动1作用下，所有楼层的层间位移角均未超过1/50，最大层间位移角位于第2层，即结构的底层；而在地震动2作用下，在峰值加速度为0.58g、0.62g时对应的层间位移未超过1/50，最大层间位移角位于第3层，但在0.719g和0.825g峰值加速度下，结构的最大层间位移超过3.5%。地震动3作用下，前3层的层间位移角没有超过规范规定的1/50，但上层层间位移超过1/50，最大层间位移集中在结构上层第5层。可见地震动输入的不同，结构的层间位移，最大层间位移有较大的区别，故地震动的不确定性影响时明显的，不可忽视的。

由于地震动输入的不同，结构的层间信息有很大的差别，这里进一步分别选取PGA=0.58g、0.825g的地震作用下，对混凝土框架结构在地震作用下进行失效模式分析，结果如图11、图12所示。

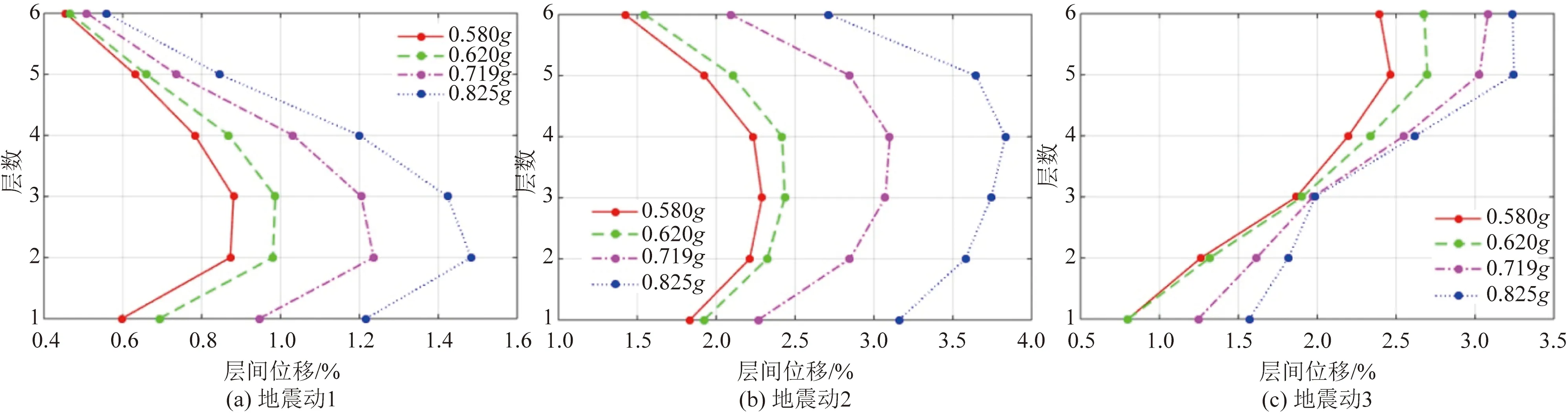
图10 不同峰值加速度层间位移角Fig.10 Story-drift of different PGA

图11 巨震作用下(0.58g)结构塑性铰分布 Fig.11 The plastic hinge distribution corresponding of mega earthquake(0.58g)

从图11和图12可以看出，在巨震作用的不同地震动输入下，塑性铰的出现也有很大区别，和大震作用下的出现规律一致。当采用同一条地震动时，巨震对应的峰值加速度不同，随峰值加速度的增大，结构的塑性铰的数量开始增加，但是其失效模式一致。图11(a)、12(a)中，1～5层全部出现梁端塑性铰，这表明两个结构能形成梁端耗能机制，之后底层柱也开始现塑性铰，符合抗震规范“强柱弱梁”准则设计。

4 结论

以六层三跨的RC框架结构为研究对象，基于OpenSees平台建立RC框架结构的数值模型，考虑了地震动的随机性。从20条地震动中选取具有代表性的3条地震动，进一步进行非线性动力时程分析，对大震、巨震作用下混凝土框架结构的失效模式进行了深入研究，得出以下结论。

(1)对于按《建筑抗震设计规范》(GB50011—2010)设计的RC框架结构，其失效模式多为屈服失效模式。其中屈服失效模式多为单层屈服失效模式、部分梁屈服失效模式。

(2)通过对塑性铰进行分析，发现塑性铰基本上先出现在中跨的梁端，柱端出现的塑性铰破坏程度高于梁端的塑性铰。

(3)对于同一条地震动，PGA不同，结构出现的塑性铰的顺序有差异，塑性铰的破坏程度不同，但是其失效模式趋于相似；地震动不同，PGA相同时，其失效模式不同，表明地震动的不确定性影响着结构的失效模式。