手臂疲劳时表面肌电信号特征
2021-09-26刘光达董梦坤许蓝予周子健李翠锶张守伟
刘光达,董梦坤,许蓝予,周子健,李翠锶,张守伟
(1.吉林大学仪器科学与电气工程学院,长春 130012;2.东北师范大学体育学院,长春 130024)
运动员获得优秀成绩的前提需要进行大量的训练,而大量的训练会增加运动员的伤病概率。因为随着训练强度和时间的增加会产生肌肉疲劳,当疲劳到达一定程度会造成肌肉损伤,所以为了避免这种情况,可以选择比较合理的生理信号,对人体的疲劳程度进行判断。而近几年,表面肌电(surface electromyography,sEMG)在评价肌肉疲劳方面备受关注。表面肌电信号是肌肉收缩时产生的微弱的生物电信号,包含了许多有用的生理信息[1]。表面肌电信号可以反映人体肌肉的功能状态,通过提取表面肌电信号特征,可以用于疲劳判断、康复医疗和诊断肌肉病等[2]。
目前已有多种基于表面肌电信号的肌肉疲劳特征被广泛使用,不同的特征参数对疲劳的评价效果也不同。例如,王宏鹏等[3]通过对高原驾驶员颈部肌电数据分析,发现随着驾驶时间的增长,颈部肌电特征积分肌电值有上升趋势,而中值频率有下降趋势,且在行驶60 min时,驾驶员进入疲劳状态。徐明伟等[4]针对颈部前屈,对颈部肌肉每60 s肌电值求其平均功率频率和积分肌电值,研究发现,积分肌电值的先增大后减小,且可用平均功率频率的导数负数积聚来判定肌肉疲劳。王琳等[5]结合生物力学理论分析颈部表面肌电信号,发现随着屈颈时间增加,积分肌电值上升,近似熵和疲劳指标Q下降,经t检验和变异系数分析可知,Q值对颈肌疲劳的反映最佳。Terracina等[6]通过提取疲劳相关特征均方根值,过零率和中值频率用来检测躯干肌肉疲劳。Jero等[7]基于阶频谱相关的肱二头肌表面肌电信号的分析,记录了来自50名健康志愿者的sEMG信号,发现随着疲劳加深近似熵和样本熵显著降低,表明使用阶频谱相关方法能够区分疲劳状态。Moniri等[8]采用浅层模型和深度卷积神经网络实时学习预测5种常见的表面肌电特征,提供了一个通用的模型,可以对于一系列的体育活动提供准确预测。
然而现在的研究主要是针对肌肉疲劳时各个特征参数的变化规律,尚未研究这些特征参数与肌肉疲劳等级的相关性程度以及联合特征参数选择。因此现针对右手臂的肱二头肌,分别从时域、频域以及时频域3个方面来分析肌肉疲劳时表面肌电特征参数,客观的比较它们与疲劳等级的相关性,从而找出更有效的联合特征参数。
1 试验方案
1.1 试验对象与试验设备
试验对象为6 名研究生,身体状况良好,年龄在23~26 岁,试验前24 h未进行高强度的运动,均为右手使用者,无神经肌肉骨骼疾病。每位实验对象在实验前都被告知实验流程,同时签订知情同意书。
选取受试者右手臂的主要发力肌肉群:肱二头肌、肱三头肌、肱桡肌为试验部位。性别、年龄、身高、体重以及身体质量指数(body mass index,BMI)如表1所示。
选用美国Delsys无线肌电仪作为表面肌电采集设备,型号 TrignoTM Wireless EMG,采样频率为1 926 Hz,拥有16 个肌电图通道,可以通过无线蓝牙设备传输到电脑软件上显示。磨砂膏、医用酒精、5 kg哑铃(用于加速肌肉疲劳进程)。
1.2 试验过程
试验前给予受试者相应动作指导帮助其熟悉主观疲劳感量表(rating of perceived exertion,RPE),然后根据个人情况进行若干次预试验使受试者熟悉试验过程。以往研究,试验多采用由记录者每隔固定时间询问受试者状态,这样容易干扰受试者,给受试者带来一定的心理压力,而且不同受试者达到疲劳程度的时间也不尽相同,容易错过相应的疲劳等级。故采用测试者根据自身主观疲劳感受主动报告主观疲劳感量表分数。

表1 受试者基本信息Table 1 Basic information of subjects
受试者闭眼放松倚靠在凳子上休息2~3 min,达到最佳身心放松状态。用磨砂膏、酒精棉清洁皮肤表面,并将Delsys肌电传感器置于右手肱二头肌、肱三头肌、肱桡肌。受试者端坐于试验桌前,颈部、背部挺直,躯干与大腿,大腿与小腿分别保持90°,左手平放在左腿上,右前臂与右上臂保持90°,略微靠近躯干。
待受试者准备完毕后,开始采集无负重状态下数据3 s;随后由操作员将哑铃放于受试者手中,保持静态等长收缩状态,然后开始采集负重状态下肌电数据。采集过程中,受试者保持恒力托举哑铃,操作员记录受试者的主观疲劳感量表得分与相应的时间,并观察受试者的右臂关节角度及抖动状况,随时了解受试者的主观感受。当受试者的右前臂与右上臂无法保持90°或者右臂剧烈颤抖时结束数据采集。重复以上操作,直至6名受试者数据全部采集完成,因受试者差异,可能采集时间与疲劳时间会略有差异,需要操作员在一旁给予适当的语言鼓励,使受试者尽可能保50 s以上的负重状态数据采集。
2 sEMG分析方法
2.1 数据预处理
表面肌电信号是一种微伏级的非平稳时变信号,其幅度范围一般在0~5 mV,其中能量大部分集中在50~150 Hz[9]。其干扰源主要来自设备的固有噪声和工频干扰,因此使用带宽为30~300 Hz的带通滤波器和50 Hz陷波器来滤除噪声干扰。
2.2 时域分析方法
表面肌电信号的时域特征能够反映信号在时间维度的变化,具有计算量简单、快速的优点,常用指标有积分肌电值(integrated electromyography,iEMG),均方根值(root mean square,RMS)[10-12]。
积分肌电值的计算公式为
(1)
均方根值的计算公式为
(2)
式中:T为选取的帧数长度;EMG(t)为t时刻对应的表面肌电信号的幅度。
2.2 频域分析方法
表面肌电的频域特征是将其时域信号通过快速傅里叶变换转变为频域信号,根据信号的功率谱或频谱进行分析,常用指标有平均功率频率(mean power frequency,MPF)、中值频率(media frequency,MF)[13]。
平均功率频率的计算公式为
(3)
中值频率的计算公式为
(4)
式中:f为表面肌电信号的频率;PSD(f)为表面肌电信号的功率谱密度函数。
2.3 时频域分析方法
表面肌电信号是一种非平稳信号,用时域和频域分析法可能会受到噪声、动作干扰等诸多影响,而时频分析法常用于分析非平稳信号。通过时频分析可以获得信号同时在时域和频域的能量分布图,从而获得时间和功率谱的能量密度信息常用指标有瞬时平均频率(instantaneous mean power frequency,IMPF)和瞬时中值频率(instantaneous median frequency,IMF)[14]。
瞬时平均频率的计算公式为
(5)
瞬时中值频率的计算公式为
(6)
式中:f为表面肌电信号的频率;PSD(t,f)为频率和时间的二维函数。
3 试验结果与分析
截取试验开始5 s后和停止前5 s的信号作为原始表面肌电信号,其中一名典型受试者(受试者1)疲劳进程中的肱二头肌、肱桡肌和肱三头肌的表面肌电信号如图1所示。
图1分别为肱二头肌、肱桡肌和肱三头肌表面肌电信号,可以看出负重状态下,随着时间的持续,3 块肌肉的幅值都有增大的趋势。但是,不同部位的幅值增大的趋势不相同,其中肱二头肌幅值增大较为明显,肱三头肌和肱桡肌幅值无明显增大趋势。分析其原因,可能是在手臂产生疲劳的过程中,肱二头肌募集更多的运动单元或者是此负荷状态下肱二头肌为主要的发力肌群,当到达某种阈值后,幅度在一定范围内浮动,基本保持不变。
本文研究选择右手臂的肱二头肌作为分析部位,原始sEMG经预处理后,分别提取时域上的RMS、iEMG,频域上的MPF、MF,以及时频域上的IMPF、IMF。大量研究发现,随着疲劳程度的加深,sEMG信号的时域、频域以及时频域特征会有不同程度的变化,如图2、图3和图4所示,可以看出时域特征RMS和iEMG随着肌肉负重时间的持续有上升趋势,频域特征MPF和MF随着肌肉负重时间的持续有下降趋势,而时频域特征IMPF和IMF随着肌肉负重时间的持续出现先短暂上升然后下降趋势,表明sEMG信号的时域、频域和时频域特征与肌肉疲劳有较好的关联性。
不同受试者以及不同sEMG特征参数往往具有不同的量纲和量纲单位,这样会影响sEMG的分析,因此有必要对这些特征的数据集进行归一化处理,使各特征参数处于同一数量级。采用的归一化的方法是最大-最小标准化,公式为

图1 受试者右手臂3块肌肉表面肌电信号Fig.1 sEMG signals of three muscles in the right arm
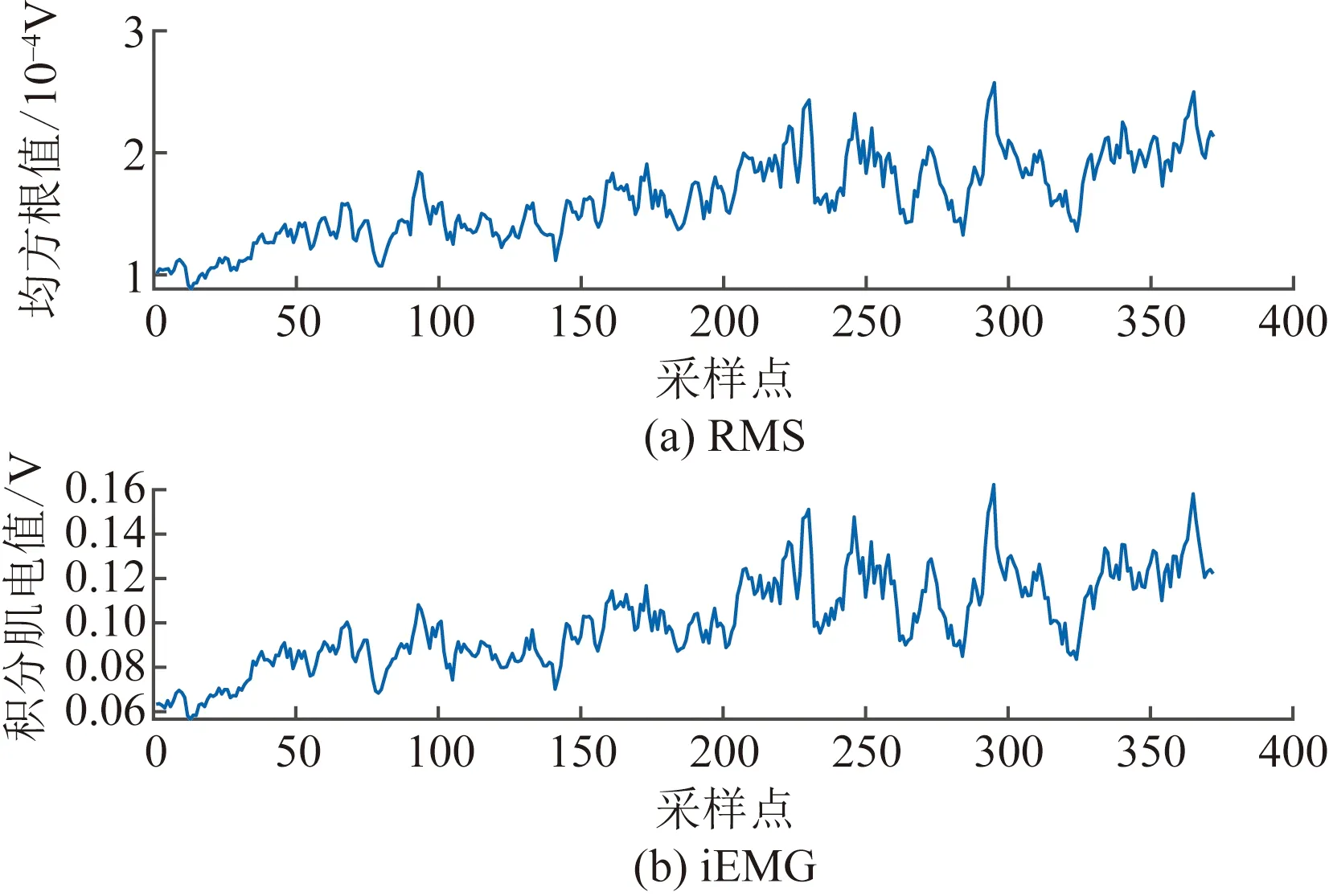
图2 肱二头肌的时域特征Fig.2 Time domain characteristics of biceps brachii
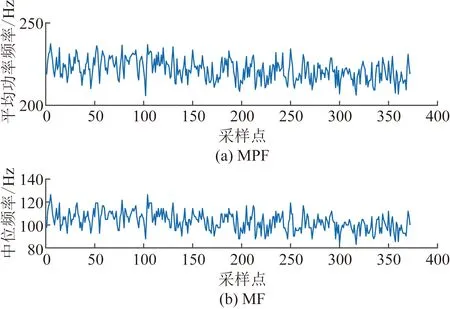
图3 肱二头肌的频域特征Fig.3 Frequency domain characteristics of biceps brachii
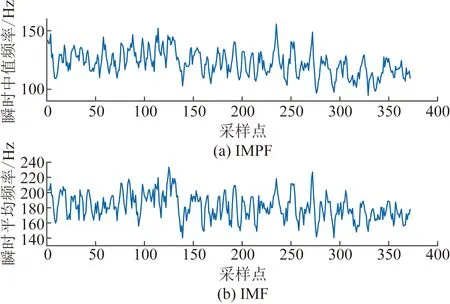
图4 肱二头肌的时频域特征Fig.4 Time frequency characteristics of biceps brachii
(7)
式(7)中:x为原始数据;minA和maxA分别为特征A的最小值、最大值。
最大-最小标准化是对sEMG数据进行线性变换,将A的原始数据x映射到区间[0,1]。
对于每名受试者,将其原始数据时间分成38段,求其每段对应特征参数的均值。然后,以时间段为自变量,sEMG的特征值为因变量,进行幂函数和指数函数的非线性曲线拟合,结果如图5~图10所示。不同拟合方式下的判定系数R2如表2所示。

图5 RMS的幂函数、指数函数拟合Fig.5 RMS power function and exponential function fitting
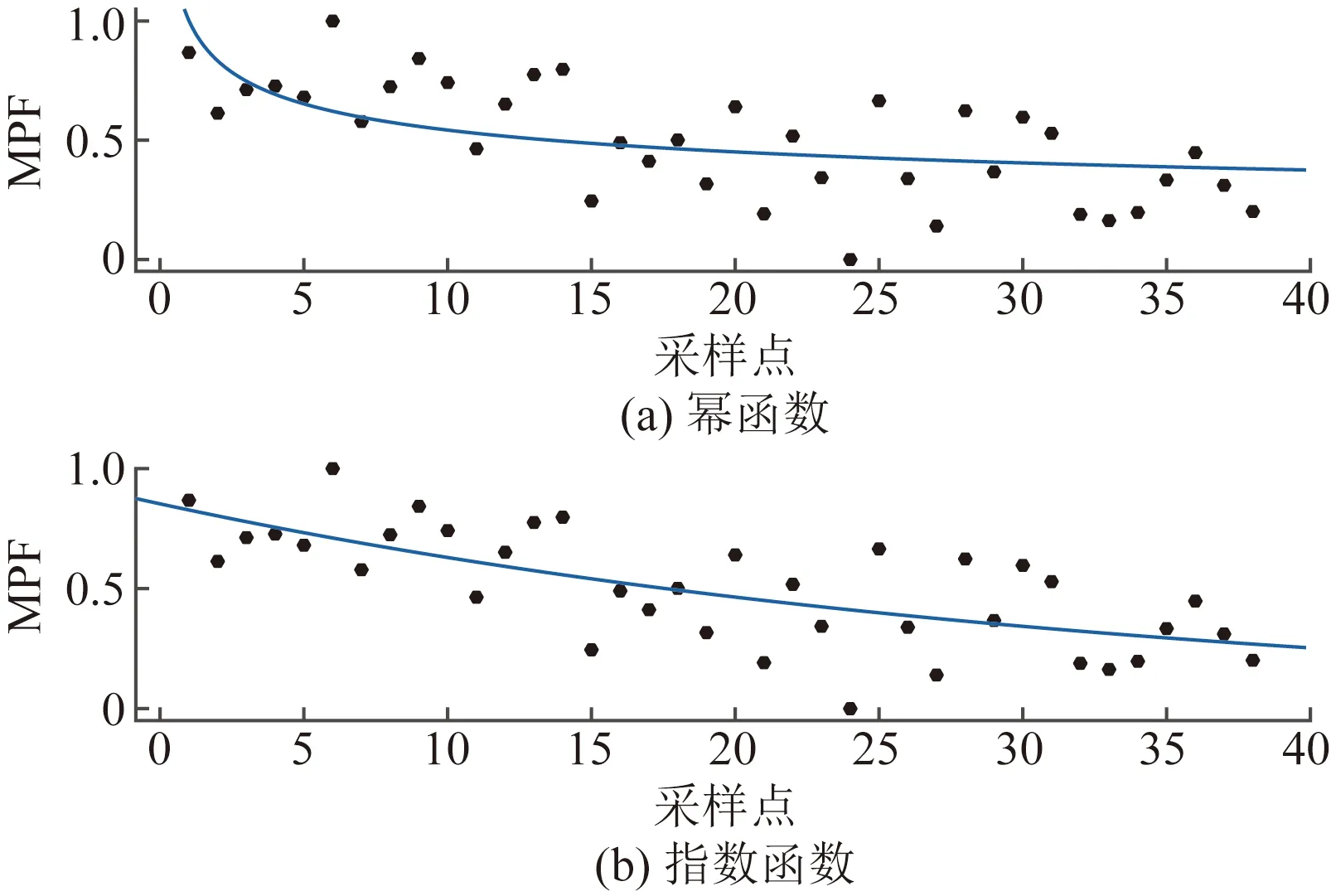
图7 MPF的幂函数、指数函数拟合Fig.7 MPF power function and exponential function fitting
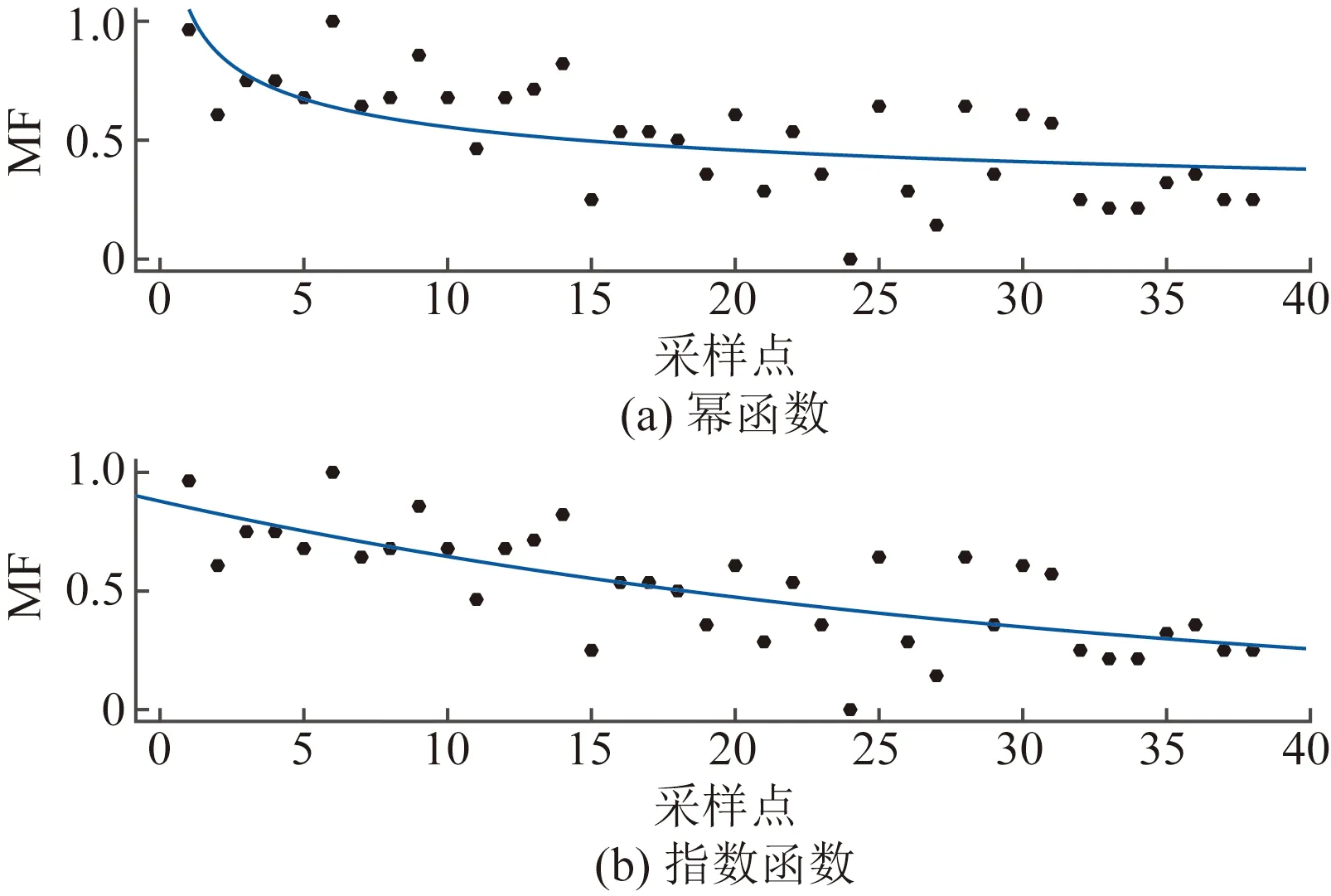
图8 MF的幂函数、指数函数拟合Fig.8 MF power function and exponential function fitting
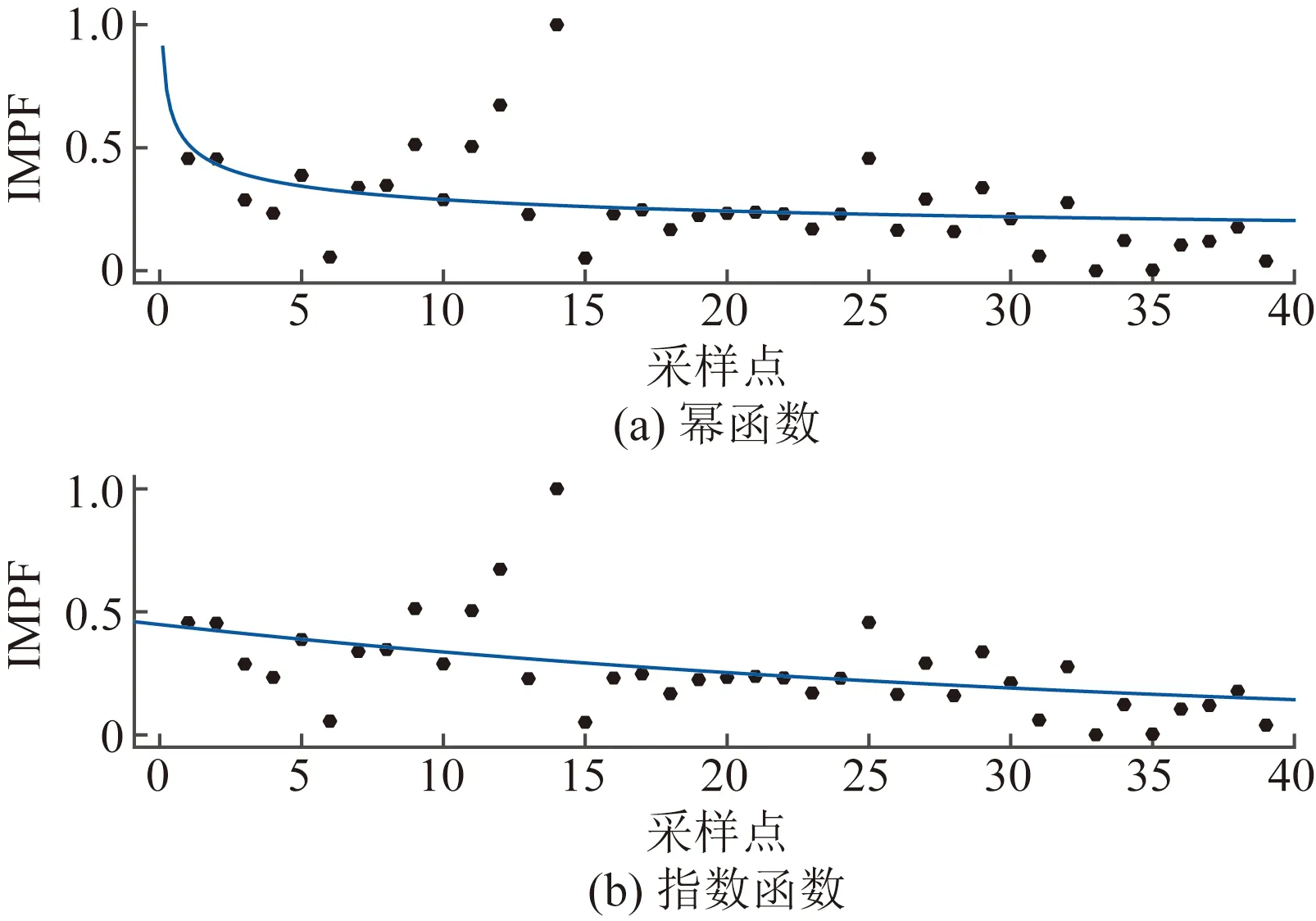
图9 IMPF的幂函数、指数函数拟合Fig.9 IMPF power function and exponential function fitting

图10 IMF的幂函数、指数函数拟合Fig.10 IMF power function and exponential function fitting
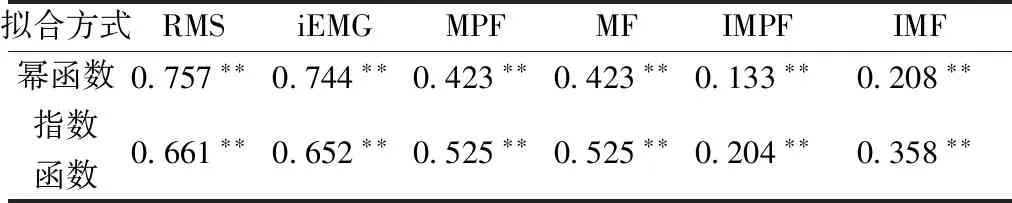
表2 不同拟合方式下的判定系数R2Table 2 Determination coefficient R2 under different fitting methods
从表2可以看出,sEMG的时域特征RMS、iEMG,幂函数拟合的判定系数R2大于指数函数拟合,而对于sEMG的频域特征MPF、MF以及时频域特征IMPF、IMF,指数函数拟合的判定系数R2大于幂函数。
但是,各拟合曲线均具有统计学意义P<0.01。
经研究发现主观疲劳感量表能够很好地反映局部肌肉疲劳状态[15],RPE对应的sEMG信号各特征均值如表3所示,利用皮尔逊相关系数算法,公式如式(8)所示,计算各特征与RPE之间的相关系数r,结果如表4所示。可以发现,各特征与RPE均有很高的相关性。
(8)
式(8)中:cov(X,Y)为变量X和Y的协方差;σX和σY分别为变量X和Y的标准差。
以受试者的RMS、iEMG、MPF、MF、IMPF、IMF为自变量,RPE为因变量,分别进行线性回归,判定系数R2如表5所示。比较其判定系数R2,可以发现RMS和MF与RPE值的拟合度更优,分别为0.916和0.750。
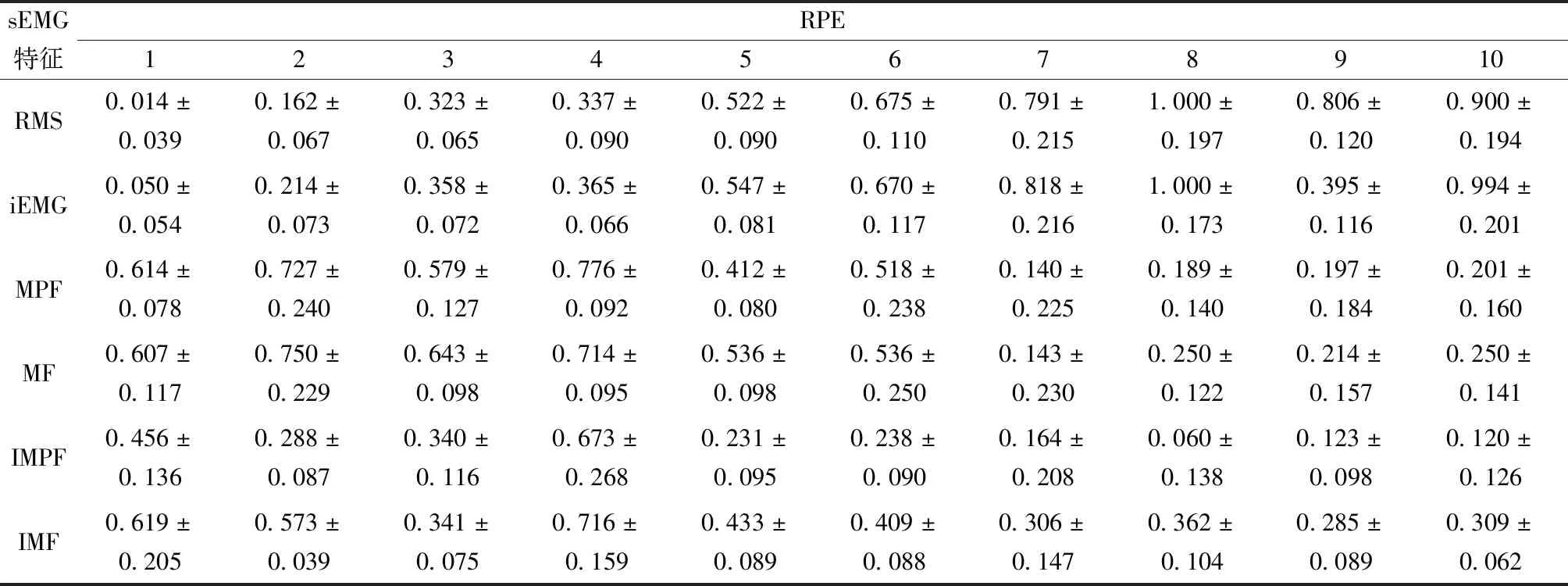
表3 RPE对应的sEMG信号各特征均值Table 3 The mean value of each feature of the sEMG signal corresponding to the RPE

表4 各特征与RPE之间的相关系数Table 4 The correlation coefficient between each feature and RPE
事实上,肌肉疲劳常常是与多个特征指标相联系的,由多个自变量中的最优组合共同预测肌肉疲劳,比只用一个特征进行预测更加有效。因此采用多元线性回归来分析肌肉疲劳与2个不同特征指标之间的关系。
多元线性回归模型经常用来描述变量y与x之间的随机线性关系,即
y=β0+β1x1+…+βkxk+ζ
(9)
式(9)中:x1,x2,…,xk为非随机变量;y为随机的因变量;β0,β1,…,βk为回归系数;ζ为随机误差项。
y、x、β用矩阵表示为
(10)
可以记为y=xβ+ζ。
利用皮尔逊相关系数算法对6个特征值进行相关性分析,计算出各个特征之间的相关系数r,如表6所示。可以发现,各特征之间存在不同程度的相关性,说明个特征之间既存在有用信息,也存在冗余信息,所以选择合理的特征参数组合尤为重要。
由表6可以看出,时域内的两个特征参数RMS和iEMG,频域内的两个特征参数iEMG和iEMG,时频域内的两个特征参数IMPF和IMF有很大的相关性。所以选取时域、频域以及时频域的不同特征指标进行组合,以不同域内的两个特征指标为自变量,RPE为因变量,建立回归模型。不同组合的判定系数R2如表7所示。
由表7可以发现,RMS和MF作为联合特征参数的线性回归模型判定系数R2最大,数值为0.921,优于其他组合模型。
4 结论
通过分析负重状态下右手臂肱二头肌疲劳的表面肌电信号,可以得到以下结论。
(1)随着负重时间的持续,时域特征RMS和iEMG有上升趋势,频域特征MPF和MF有下降趋势,而时频域特征IMPF和IMF出现先短暂上升然后下降趋势。
(2)对各个疲劳特征采用不同的非线性拟合方法,发现对于sEMG的时域特征RMS、iEMG,幂函数拟合的判定系数R2大于指数函数拟合,而对于sEMG的频域特征MPF、MF以及时频域特征IMPF、IMF,指数函数拟合的判定系数R2大于幂函数。

表5 RPE与各特征拟合判定系数R2Table 5 RPE and each feature fit determination coefficient R2

表6 各特征之间的相关性Table 6 The correlation between the features

表7 不同组合的判定系数R2Table 7 Determination coefficient of different combinations R2
(3)利用皮尔逊相关系数算法计算各个特征与RPE的相关系数r,发现各个特征参数与RPE均具有较高的相关性,其中RMS与RPE的相关系数最大,为0.957。
(4)比较一元和多元线性回归的判定系数R2,可以发现,多元回归模型对于疲劳判断更优于一元回归模型,其中时域特征RMS与频域特征MF的组合较于其他组合更能判断疲劳程度。表明RMS和MF相结合作为评估肌肉疲劳的联合参数更优。
